基于最大熵准则的Wigner-Ville分布与微型古河道刻画方法及应用

徐天吉 ，程冰洁 ，牛双晨，秦正晔，王贞贞

（1. 电子科技大学资源与环境学院，成都 611731；2. 电子科技大学长三角研究院（湖州），浙江湖州 313000；3. 成都理工大学“油气藏地质及开发工程”国家重点实验室，成都 610059；4. 成都理工大学“地球探测与信息技术”教育部重点实验室，成都 610059；5. 四川中成煤田物探工程院有限公司，成都 610072）

0 引言

平直、蛇曲、辫状等类型多样的河流相，多年前就已经成为油气领域的研究热点。在俄罗斯西西伯利亚、美国怀俄明州及中国的鄂尔多斯盆地、四川盆地等区域，已经发现了许多河流相大型和中型油气田。但是随着中国油气勘探开发程度的不断深化，目前河流相资源目标已经由大型、中型逐渐转向微型油气藏。微型古河道广泛分布在陆相与海陆过渡相的浅、中、深等各类地层，油气储量丰富，勘探潜力巨大，但具有河道宽度窄、砂体薄、油气聚集复杂等不利特征[1-2]。此外，随着埋藏深度的增加，地震反射表现出能量弱、低频为主、频宽窄等不利特征，垂向与横向分辨率降低，制约了窄古河道、薄储集层及其他油气信息的精确提取。微型古河道的识别，已经成为增加井位部署、水平井钻采等勘探开发风险的突出难题。

针对微型古河道的识别难题，目前主要从地震采集、处理和解释等角度着手，利用高分辨地震数据获取古河道的横向宽度、垂向厚度等关键参数和空间展布特征。就高分辨地震采集而言，尽管在高密度、“两宽一高”（宽方位、宽频带、高密度）等先进观测系统下采集到的地震资料，提升了浅中层油气藏预测与描述精度，但是面对深层地质目标，至今未能突破震源能量衰减快、检波器难以接收到高频有效信号等激发与接收方面的“瓶颈”问题。就高分辨地震资料处理与解释而言，尽管形成了反Q补偿[3]、谱整形[4]、频宽拓展[5]、薄层反射系数反演[6]、低频扩展深度学习[7]、高分辨阻抗反演[8-9]等方法，可以使地震数据“无中生有”地出现更多的反射轴、波阻抗界面增加等现象，但存在信噪比降低、波组有效性评估难、甚至出现假反射界面等特征，必然降低地质预测的可靠性。同时，埋藏越深、规模越小的微型古河道的识别难度越大；尤其是极窄、流向复杂的微型古河道，需要从地震波的传播能量、反射频率等角度出发，不断探索突破地震分辨率极限的有效方法，才能逐步解决微型古河道的识别难题。

识别微型古河道的关键，是基于高分辨时频分析方法提取地震信号的高分辨时频响应特征，利用地震波的能量、频率、相位等信息，有效刻画微型古河道的宽度、流向等特征。目前，反Q补偿、频宽拓展等许多高分辨处理与解释方法，均以时频分析为基础，却未实现高分辨时频响应特征提取，致使类似微型古河道的小规模地质目标难以实现高清识别。其实，自1946年Gabor首次提出了声波信号的频谱图后[10]，迅速形成了线性、双线性和非线性 3大类核函数不同的时频分析方法[11]。其中，Gabor变换、短时傅里叶变换（STFT）、连续小波变换（CWT）、S变换（ST）和广义 S变换（GST）等属于线性时频分析方法，虽具有计算效率较高的优势，但多数具有窗口依赖性，且受海森堡（Heisenberg W）不确定性原理控制[12]，时间和频率的分辨能力不能同时提升。自适应 STFT[13]、模态分解[14-15]、同步挤压小波变换[16]、匹配追踪（MP）[17]等属于非线性时频分析方法，虽具有分辨率较高的优势，但计算量较大，鲁棒性不足，难以适应低信噪比信号时频分析。Wigner-Ville分布（WVD）[18]、伪Wigner-Ville分布（PWVD）、平滑伪Wigner-Ville分布（SPWVD）和Choi-Williams分布（CWD）[19]等属于双线性（又称二次型）时频分析方法，不受海森堡不确定性原理约束[12]，优良的数学性质为高分辨时频分析奠定了良好的理论基础。

本文基于信号最大熵准则（Maximum Entropy Principle），在克服 WVD交叉项干扰的前提下，研究增强 WVD频谱聚焦特性和提升地震信号时频分辨率的方法，以突出窄细古河道响应特征。并采用仿真信号、正演数值模拟等理论数据开展试验与论证分析，以形成微型古河道识别新方法，为井位部署、水平钻井等提供支撑。

1 方法原理

1.1 最大熵准则

熵（Entropy），是指离散随机事件或特定信息的出现概率，由Shannon C E在1948年首次定义，主要用于表征随机变量或特征信息的不确定性[20]。1957年，Jaynes E T 提出了最大熵准则，即在先验信息准确的前提下，最能代表当前信息状态的概率分布，是熵最大的概率分布，换言之，当符合先验信息的概率分布具有不确定性时，熵最大的信息分布是合理的[21]。

1967年，Burg将最大熵准则引入信号频谱分析中，形成了最大熵时频分析Burg算法[22]。Burg认为，熵是信号X的分布函数，仅与X的取值概率有关，而与实际取值无关。当信号X的取值为x时，分布密度函数为p(x)，则其熵H(x)为：

此时，Burg定义信号X的功率谱熵为：

当利用（2）式求取功率谱时，需要在H[P(f)]最大的条件下，递推求解信号X的自相关函数，使功率谱误差最小，分辨率获得提升。其实，Burg算法等价于线性自回归AR（Auto Regressive）预测模型，最大熵功率谱P(f)的计算公式[22]为：

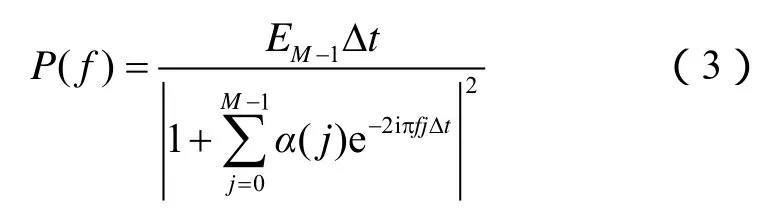
1.2 离散Wigner-Ville分布与功率谱

1992年Boashash定义[23]连续时序信号x(t)的解析信号为z(t)时，Wigner-Ville分布（WVD）为：

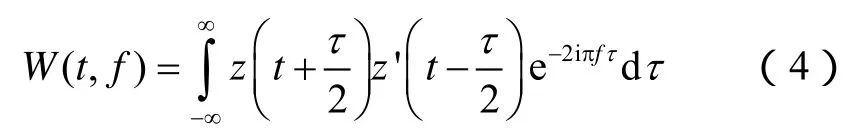
然而，实测的信号并非连续信号，实际应用时，需要对W(t,f)进行离散化。设x(t)、z(t)的离散表达式分别为x(n)和z(n)（0 ≤n≤N-1），对x(n)作希尔伯特（Hilbert）变换，在计算出z(n)后即可获得W(t,f)的离散表述：

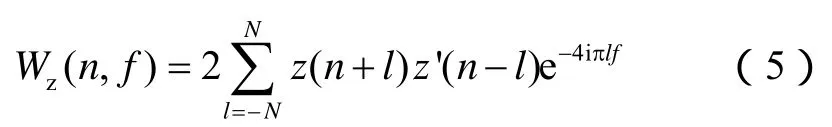
据WVD的性质可知，离散WVD是对瞬时自相关函数进行离散傅立叶变换。离散信号的瞬时自相关函数为：

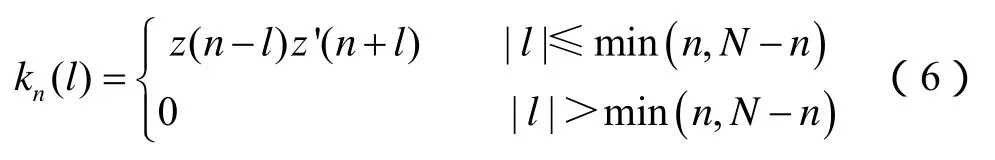
对于每一个样点n，kn(l)将组成一个卷积核序列kz(n)，如（7）式。当n=0和n=N- 1 时，卷积核序列kz(n)=kz(0)和kz(n) =kz(N- 1)最短；当时，最长。以kn(0)为中心，对kz(n)左右补充0值，可将kz(n)扩充为长度为N的卷积核序列。

对第n个采样点的卷积核序列kz(n)，进行离散傅立叶变换，即可获得WVD瞬时功率谱，如下：

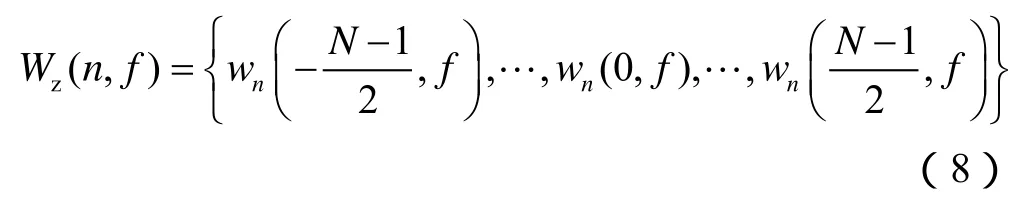
其中，Wz(n,f)的子项可表述为：

通过计算每一个采样点n对应的瞬时功率谱，最终可以得到离散信号x(n)的Wigner-Ville功率谱，即：

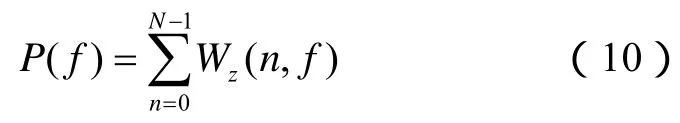
当然，受 WVD双线性的影响，在利用瞬时自相关函数kn(l)前后数据相乘时，将产生交叉项干扰，不利于高精度功率谱特征分析。

1.3 最大熵准则约束下的Wigner-Ville功率谱计算方法

当瞬时自相关函数kn(l)的一阶导数为0时，求得的Wigner-Ville分布即为最大熵谱。由于一维最大熵谱与自回归模型AR谱是等效的，故只需要求得AR模型参数、计算出 AR模型谱，就能获得最大熵谱[24]。这样，可以避免利用（10）式计算功率谱，绕开瞬时自相关函数前后数据相乘时产生的交叉项干扰。

基于 Burg算法求取最大熵功率谱P(f)时，（3）式与（10）式是等效的，只需基于Levinson-Durbin递推规则[25]，在求取预测误差E、自回归系数a等 AR模型的参数后，代入（3）式就能获得最大熵准则约束下的WVD功率谱。Burg算法通过前向预测误差和后向预测误差，递推 AR模型的自回归系数[26-27]。将设为初始条件，递推公式如下：

通过离散信号x(n)及其解析信号z(n)，可以计算预测误差的初始功率，即

利用m阶前向预测误差和后向预测误差，可以计算预测误差的平均功率，即

据Levinson-Durbin递推约束规则，设am(j)为M阶AR模型在阶次序号为m时的第j个自回归系数，Em为m阶次时的最小预测误差，则其递推关系为

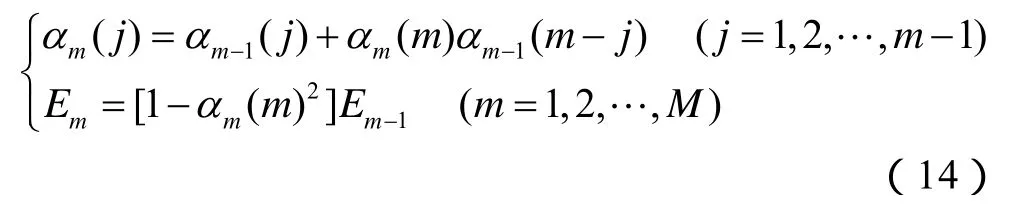
这样，将am( 1)，am( 2)，…，am(m- 1)和Em代入（3）式，就能计算出 WVD最大熵功率谱。WVD最大熵功率谱在时间域和频率域的分布，即为Wigner-Ville最大熵时频谱（简称MEWVD）。

概括起来，Burg算法的WVD最大熵功率谱的计算步骤[28]主要包括：①设m=1，计算P0(f)、EF,0(n)与EB,0(n)；②计算am(m)；③计算阶次为m时的第j个自回归系数④计算Pm(f)；⑤计算阶次为m时的EF,m(n)和EB,m(n)；⑥设m=m+1，重复②—⑤，直到Pm(f)不再明显减小时，利用Levinson-Durbin递推关系，可以获得AR模型的参数，最终计算出WVD最大熵功率谱。

在时间域，MEWVD并未将瞬时自相关函数前后数据相乘，而仅使用当前n点附近的数据，避免了交叉项干扰；在频率域，受最大熵准则约束，使每个n点对应的功率谱更精确，能量更聚焦。同时，在最大熵的前提下，采用Levinson-Durbin约束递推未知瞬时自相关函数，使计算的功率谱误差减小，提升了信号时频分辨能力。

需要指出的是，最大熵准则在数学、经济、信息等领域被广泛应用，主要优势在于其不仅保留了信息分布的不确性时，同时将预测风险降到了最低。在油气领域，常常面对横向较窄、纵向较薄的古河道、砂坝、点礁等微型地质体，地震波衰减、调谐、噪声等因素增加了微型地质体的预测难度，计算高精度、高聚焦性的地震功率谱，是识别微型地质体的重要基础。MEWVD在熵最大时计算最能代表微型地质体的地震频谱响应特征，不仅能实现时频特征的分类取优，而且可以在噪声环境下提高信号分析的鲁棒性[29]，有利于提升微型地质体识别的可靠性。

2 方法实验

2.1 仿真地震信号的MEWVD实验及定量分析

地震波在地下传播时，受地层埋深、孔隙度、填充流体等因素影响，将产生能量衰减，引起动力学、运动学和几何学等特征发生变化。采用振幅、吸收系数、频率、相位和走时等参数，可以仿真描述地震波传播过程，如下：

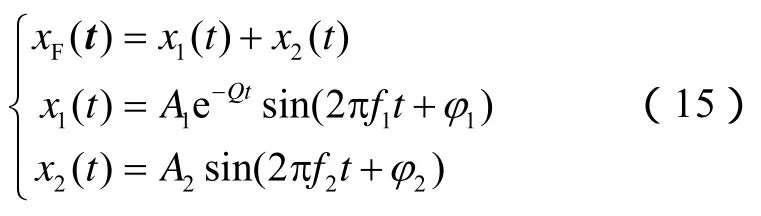
上式中，仿真地震信号xF(t)分别由衰减分量x1(t)和平稳分量x2(t)叠加而成。其中，x1(t)包含了吸收系数、振幅、频率、相位和走时等参数，x2(t)不包含吸收系数，传播能量将不会产生衰减。

为了对比分析地震波传播过程中的时频特征，利用xF(t)的参数，构造出了关联特征较强的高、低频能量强弱不一样的仿真地震信号。如表1，信号xF1和xF2的起始能量A1和传播时间t相同，xF1中A2、f2、j2为0，表示xF1仅由衰减分量构成，且其A1、f1和Q均较大，类似强能量、高频和强衰减的地震信号。xF2包含了xF1，仅通过改变f2，在xF2的基础上增加了低频、弱振幅的平稳分量，意味着xF2在t时间内的传播能量、振幅等将随频率变化而改变。如图 1a和图 1b中第 1列，分别显示了xF1和xF2的波形特征。可见，xF1随着t的变化，振幅减弱，能量衰减很快；xF2随着t的变化，振幅减弱，能量也在衰减，但衰减分量的控制作用越来越弱，在信号传播约0.25 s之后，信号主要受平稳分量控制，且由于f2差异，使xF1振荡周期短、波形“瘦”，xF2振荡周期长、波形“胖”。

表1 仿真地震信号的参数描述

同时，对比不同的时频分析方法，发现 MEWVD具有非常优良的时频聚焦特性和分辨率。如图1a和图1b，第 2列显示了仿真地震信号的快速傅里叶变换（FFT）频谱，揭示信号xF1的能量峰值聚集在80 Hz，xF2的能量峰值聚集在10 Hz和80 Hz。第3至10列，分别显示了 STFT、GST、CWT、WVD、PWVD、SPWVD、CWD和 MEWVD等方法的时频效果。对比分析，尽管xF1和xF2的最强能量均聚集在 80 Hz高频位置，但是，不同的时频分析方法显示的能量聚焦程度与频率分辨能力存在差异，且MEWVD聚焦效果与分辨率最优、WVD次之、STFT最弱。GST和CWT的时频分辨能力相似，对80 Hz高频强振幅与10 Hz低频弱振幅均能有效识别，但能量聚焦程度、时间分辨能力等较MEWVD差。此外，WVD时频特征还存在交叉项干扰，PWVD虽在一定程度上压制了交叉项干扰，但能量聚焦性减弱，降低了xF2的低频、弱振幅信息的分辨能力；SPWVD和CWD基本压制了交叉项干扰，但也几乎无法有效识别xF2中低频、弱振幅响应，较 PWVD的分辨率损失更严重。

图1 仿真地震信号及不同时频分析方法呈现出的频谱响应差异

2.2 窄薄数值模型MEWVD实验及效果分析

为了进一步证实 Wigner-Ville最大熵时频谱（MEWVD）的频谱聚焦性和时频高分辨能力，采用表2所示参数，设计出二维数值模型，包含了埋深、宽度和厚度各异的窄薄地质体，其“透镜状”的地质特征与微型古河道的横截面类似。基于二维地震波动方程正演数值模拟方法，以35 Hz的Rick子波作为点震源激发，以10 m采样间距、1 ms采样率接收，获得了正演模拟记录。模型④—⑨的砂体厚度逐渐变薄、宽度逐渐变窄；模型④—⑥较宽、厚度大于 1/4波长（约30 m），顶底界面的反射同相轴明显，而⑦—⑨较窄、厚度小于1/4波长，地震记录表现为谐波反射，且⑦和⑧表现出强调谐反射，极薄、极窄的⑨则表现为弱调谐反射（见图2）。

表2 数值模型参数描述

图2 窄薄各异模型的单道模拟地震信号及MEWVD等频谱特征

分别抽取代表模型④—⑨的单道地震信号，计算MEWVD后，可分析模型的时频差异。如图2，显示了模型④—⑨的单道地震信号及MEWVD频谱特征，可见，窄薄各异的数值模型的反射信号，MEWVD均表现出了较强的频谱聚焦性和高分辨特征。其中，模型④—⑥较宽、较厚，单道地震信号表现出明确的顶底界反射，MEWVD在频率轴方向表现出较窄的频谱分布。模型⑦—⑨较窄、较薄，单道地震信号仅显示出了顶界面的反射，底界面受波场调谐作用而难以识别。MEWVD在频率轴方向表现出较宽的频谱分布，且厚度越薄、频谱分布范围越宽。

在单频剖面上，MEWVD的频谱聚焦性非常显著，不同频率的功率谱展现出了不同的时频分辨率。如图3，显示了正演地震信号的瞬时振幅及25，35，45 Hz的MEWVD频谱特征。其中，图3a显示瞬时振幅受时频分辨能力的局限，仅较厚的模型④表现出了顶底界面清晰的“双轴”强瞬时振幅特征，而厚度逐渐减薄的模型⑤—⑨却表现为“单轴”强瞬时振幅分布，连厚度大于1/4波长的模型⑤和⑥的顶、底界面也难以有效识别。图3b—图3c分别显示了3种频率的MEWVD频谱分布，且均比瞬时振幅具有更高的分辨率，但不同频率的 MEWVD频谱响应各异。其中，45 Hz的MEWVD频谱分辨率最高，可以准确识别窄薄模型⑤和⑥的顶底界面及横向宽度。35 Hz的MEWVD频谱分辨率次之，也能够有效识别⑤和⑥的顶底界面及横向宽度，对极窄、极薄模型⑧和⑨的频谱聚焦响应优良，且受不同宽度的影响，二者的频谱分布厚度相近、宽度差异显著。进一步分析极窄、极薄模型⑧和⑨，二者厚度相同、宽度差 5倍，瞬时振幅横向差异不明显，MEWVD频谱异常显著。尤其在图3d中，45 Hz高频聚焦性极好，显示出了厚度一样、宽度差 5倍的MEWVD频谱异常特征。同时，虽然25 Hz的MEWVD频谱分辨率总体不如35 Hz和45 Hz的频谱，但是对极窄、极薄模型⑧和⑨的频谱聚焦响应却有明显差异。其中，35 Hz和45 Hz的频谱表现为“团状”现象，而25 Hz的频谱却表现出“层状”频谱聚焦现象，表明Wigner-Ville最大熵谱与地震信号的强弱无关，当调谐作用使模型顶底界面的功率谱分布不确定时，熵最大的功率谱即为最合理的分布。

图3 正演地震信号的瞬时振幅及25，35，45 Hz的MEWVD频谱特征

总之，仿真地震信号和窄薄正演数值模型实验表明，MEWVD具有良好的频谱聚焦性和时频高分辨能力。MEWVD能够精确表征信号的时频分布，且不同频率的MEWVD能够准确获取不同尺度窄薄模型的频谱响应；同时，由于Wigner-Ville最大熵谱仅与频谱分布概率相关，当地质体较窄或薄度小于1/4波长而发生调谐作用时，利用地震反射同相轴不能直接识别，熵最大的功率谱即为地质体的最合理的分布空间。因此，综合不同频率的MEWVD频谱特征，可以识别类似窄薄模型的微型古河道的空间分布。

3 应用案例

四川盆地是一个多旋回富气沉积盆地，截至2020年，在震旦系、寒武系、志留系、石炭系、三叠系、侏罗系等27套层系中，已经发现了构造、构造-岩性、岩性-构造和岩性4类气藏，形成了四川盆地东北部、西部、南部和北部 4大工业气区[30-31]。其中，川西气区的侏罗系沙溪庙组气藏，主要分布在西邻龙门山推覆构造带、东接川中隆起区的川西坳陷。在川西东斜坡地区，发现了埋深小于3 100 m的大型岩性-构造气田——中江气田。

中江气田面积为2 350 km2，区内侏罗系沙溪庙组以浅水三角洲沉积为主，在三角洲平原亚相中发育分流河道、分流间湾、河口坝、决口扇等沉积微相。其中，分流河道主要发育细—中粒岩屑长石砂岩、长石岩屑砂岩、岩屑砂岩和岩屑石英砂岩等砂岩储集层，平均孔隙度达 8.94%，平均渗透率达0.5×10-3μm2。目前，针对资源丰富的沙溪庙组气藏，已投产工业气井约150口，日产气超过 220´104m3。然而，随着开发程度的深化，微型分流河道气藏更加隐蔽，储集层以条带状叠置薄层河道砂体为主，横向宽度窄，纵向厚度薄，精细刻画难度极大。需要探索窄细微型古河道的精确识别方法，为气藏描述、水平钻井、水力压裂等提供支撑。

中江气田侏罗系中统沙溪庙组划分为上（J2s1）、中（J2s2）、下（J2s3）共 3段；其中，J2s3段由 J2s31、J2s32和 J2s33组成。依据古河道和砂岩沉积特征，J2s33层被细分为J2s33-1和J2s33-2小层。目前，J2s33-2小层是主力产气层，层内网状和条带状古河道主要沿北东流向南西，延伸长度18～58 km，宽度0.2～3.5 km，砂厚6.5～45.2 m。储集层呈席状、箱状和钟型分布，表现为低频、“亮点”、“空白”等地震反射特征，沿古河道方向，地震反射总体较连续、稳定，垂直河道方向，呈“透镜状”或弱反射异常。

近几年，随着中江气田 J2s33-2小层气藏的深入开发，宽度小于500 m、厚度小于35 m的窄薄古河道砂岩成为重点目标，微型古河道的精确识别也成为气藏开发的关键环节。然而，受埋藏深度、宽度、厚度、岩性、物性等多种因素的影响，不同的微型古河道呈现出明显的地震反射差异。如图4a图显示J2s33-2小层的地震主频约30 Hz，频带8～70 Hz；图4b显示E井J2s33-2小层古河道出现砂体GR低值异常，地震反射为局部双波峰“透镜状”异常，预测河道宽约354 m、厚约35 m；图4c显示D井J2s33-2小层古河道出现GR低值异常，预测河道砂岩宽约310 m、厚约30 m，较E井河道更窄、更薄，“透镜状”反射更弱；图4d显示C井J2s33-2小层古河道出现GR低值异常，预测河道砂岩宽约248 m、厚约30 m，与D、E井相比较，“透镜状”异常消失，呈弱反射响应。显然，通过对比图4中的C、D、E井微型古河道地震反射特征，随着宽度变窄、厚度减薄，河道隐藏性增强，地震反射越弱，识别难度越大。

图4 目标地层地震振幅谱及典型井微型分流河道地震反射剖面

采用Wigner-Ville最大熵时频谱计算方法，提取了中江气田沙溪庙组的MEWVD频谱特征，发现不同宽度和厚度的微型古河道呈现出了不同的MEWVD异常，揭示了窄细古河道的空间展布。如图5a显示的瞬时振幅剖面上，E井J2s33-2小层古河道出现瞬时振幅强异常，异常范围较大，聚焦性较差，分辨率较低；图5b—图5d显示的MEWVD频谱剖面上，E井J2s33-2小层古河道出现强异常，异常范围随着频率的增加而减小，聚焦能力增强，分辨率提高。比较瞬时振幅与25 Hz、35 Hz的MEWVD频谱特征，在45 Hz的MEWVD剖面上，分辨能力更高，纵向频谱被分开，横向频谱收窄，频谱异常由“团状”变化为“双层状”，与砂体GR低值异常更加吻合，有效地揭示出了E井J2s33-2小层35 m薄古河道砂岩的顶底界面。可见，利用MEWVD频谱异常，能够有效刻画窄细古河道的纵向分布。

图5 E井瞬时振幅及25，35，45 Hz的MEWVD频谱特征

同时，利用MEWVD频谱异常，还能刻画微型古河道的横向展布。如图6a瞬时振幅高值异常刻画出了相对较宽的Ⅰ—Ⅳ、Ⅵ、Ⅷ号主河流的沿层展布；但在黑色框示区域，河道很窄、河道砂岩很薄，地震反射能量较强，分辨率低，利用瞬时振幅无法识别窄细古河道的空间位置、宽度和流向。在图 6b中，利用MEWVD方法获得的25 Hz频谱出现高值异常，不仅刻画出了较宽的Ⅰ—Ⅳ、Ⅵ、Ⅷ号主河流的沿层展布，而且中低值异常刻画出了更窄的Ⅴ和Ⅶ号河道的空间展布；尤其在左侧黑色框内，Ⅴ和Ⅶ号河流的宽度和流向非常清晰。与Ⅰ—Ⅷ微型河道比，Ⅸ号河道更窄，且流向弯曲变化较大，隐蔽性更强，利用瞬时振幅和25 Hz频谱难以识别，而在35 Hz和45 Hz的MEWVD频谱特征中，Ⅸ号曲流河道的沿层特征却非常清晰。由图6可见，MEWVD较瞬时振幅分辨更高，且不同频率的MEWVD频谱特征，可以识别不同宽度的窄细河道。当然，由于任何物质都有相应的敏感频段，河道也不例外，Ⅴ和Ⅶ号河道对低频更敏感，故在35 Hz和45 Hz的MEWVD频谱特征中反而不如25 Hz刻画更清晰（见图6黑色方框），但整体规律仍然是高频频谱刻画效果更佳。

图6 瞬时振幅及25，35，45 Hz的MEWVD分别刻画的J2s33-2小层微型古河道的展布

采用RGB融合（红、绿、蓝混合生成其他色彩）显示方式，将不同频率的MEWVD频谱进行融合，能更清晰的展示不同宽度和厚度河道的空间分布。如图7a显示了采用 RGB融合方式，将 25，35，45 Hz的MEWVD频谱进行融合，有效刻画出J2s33-2小层Ⅰ—Ⅸ号古河道的展布；尤其是具有极窄特征的Ⅴ、Ⅶ和Ⅸ号河道，以及Ⅷ号河道以东、Ⅵ号河道以西的更多微型古河道（红色箭头所指），也精确地揭示出了其宽度和流向等空间信息。当然，结合区内沉积构造背景，利用岩心分析与测井解释资料，可以证实采用MEWVD

频谱异常识别微型古河道的可靠性。如图7b所示，在纵向上，D井主要发育分流河道、分流间弯、河口坝等三角洲前缘沉积微相。其中，J2s33-2小层以分流河道沉积微相为主，声波时差和伽马测井曲线表现出低值响应特征，深侧向和浅侧向电阻率曲线表现出高值异常。在分流河道中部2 869.57～2 871.49 m井段的钻井取心显示，古河道水平层理发育，在较强的水动力作用下，沉积形成了厚度约30 m的致密砂岩储集层。受岩性、物性、厚度等因素影响，储集层与围岩的阻抗差异不大，在图4c所示的“透镜状”河道反射较弱，但在图6和图7却具有较突出的MEWVD频谱异常。可见，综合地震反射、钻井取心、测井响应等信息，利用MEWVD频谱异常刻画微型古河道具有较高可靠性。

图7 中江气田J2s33-2小层RGB融合MEWVD刻画河道分布及D井沉积相测井解释

此外，MEWVD频谱异常还可以刻画断层分布特征，但断层与古河道具有显著的MEWVD差异。如图6d和图7a显示，中江气田沉积构造环境整体比较稳定，在试验工区南部仅发育少量近东西向的断层，裂缝不发育。断层的MEWVD频谱异常表现为上盘与下盘边界频谱较强、中间的频谱较弱。断层与古河道虽皆呈细长条带状，但古河道边界频谱较弱、中间频谱较强。可见，断层与古河道的MEWVD频谱异常虽有相似之处，却也存在显著差异。本质上，二者的共性与差异皆由地质环境决定，这些地震响应被MEWVD异常精确的刻画了出来。

总之，MEWVD频谱聚焦性较强，时频分辨率较高，且不同频率的MEWVD对窄细不同的河道具有不同程度的敏感性，有效的揭示了中江气田沙溪庙组微型古河道的宽度、砂岩厚度和流向等空间信息。

4 结论

熵最大时的频谱特征，最能代表地震信号的频谱分布状态，MEWVD不仅避免了 WVD产生的交叉项干扰，而且最大程度的增强了频谱聚焦性，有效提升了地震信号的时频分辨率。

仿真地震信号和窄薄模型正演模拟信号试验揭示，较STFT、GST、CWT、WVD、PWVD、SPWVD、CWD等方法，MEWVD能更加精确的提取信号频谱特征；尤其是针对窄薄各异的数值模型，由于最大熵的差异而表现出了特殊的频谱响应，采用不同频率的MEWVD能够准确的识别尺度各异的窄薄地质体。

基于最大熵准则与 Wigner-Ville分布的微型古河道识别方法，充分发挥了MEWVD频谱聚焦性较强、时频分辨率较高等优势，有效的识别出了中江气田不同尺度的微型古河道，且不同频率的MEWVD对窄细各异的河道具有不同程度的敏感性，准确地刻画了微型古河道的宽度、砂岩厚度和流向等空间信息。

符号注释：

a——自回归系数，又称为预测误差因子，无因次；am——序号为m的自回归系数，无因次；1A——衰减分量的振幅，dB；A2——平稳分量的振幅，dB；E——预测误差，W/Hz；EB，m——序号为m的后向预测误差，W/Hz；EF，m——序号为m的前向预测误差，W/Hz；f——信号的频率，Hz；f1——衰减分量的频率，Hz；f2——平稳分量的频率，Hz；GR——自然伽马，API；H——熵函数，无因次；i——虚数单位；j——自回归系数am的序号，无因次；kn——自相关函数，无因次；kz——kn的卷积核，无因次；l——离散信号扩展采样点序号，无因次；m——am、EF，m、EB，m、wn等函数的序号，无因次；M——AR模型的阶数，无因次；n——离散信号采样点序号，无因次；N——离散信号长度，无因次；p——分布密度函数，无因次；P——功率谱，W/Hz；P0——初始功率谱，W/Hz；Pm——平均功率谱，W/Hz；Q——吸收系数，无因次；Rlld——深侧向电阻率，W·m；Rlls——浅侧向电阻率，W·m；t——时间，s；W——连续WVD函数，W/Hz；Wz——离散WVD函数，W/Hz；wn——Wz的子项，W/Hz；X——信号，无因次；x——某时段信号，dB；x1——衰减分量，dB；x2——平稳分量，dB；Dt——时间采样率，s；xF——仿真信号，dB；j1——衰减分量的相位，rad；j2——平稳分量的相位，rad；t——时延，s；z——离散信号，dB。