基于神经网络的松材线虫病树统计
雷皓辰
(武汉邮电科学研究院,湖北 武汉 430073)
松材线虫病疫情传染性极强,松树感染后极易死亡,因此一直被视为高危外来入侵物种,属于森林疫情监测的重要防控病害。松材线虫病迅速蔓延到中国的各个地区,已表现出疫情区域多、传播范围广、扩散面积大的情况[1],成片的松树枯萎破坏了自然环境,浪费了大量林业资源,随之而来的就是森林经济的危机。导致这种局面的形成有多方面的原因,最主要的原因还是疫情监控力度不到位。严格监控松林疫情,之后提早清除感染源是解决松材线虫病害最好的方法。
传统的人工监测方法使用大量护林员实地统计疫情发病情况,耗费了大量的人力和物力。当松材线虫疫情在大片松林中广泛分布时,人工监测更加困难。如今面对这样的情形,使用无人机可以解决监测时遇到的困难。无人机航拍是指在无人机上安装小型监控设备,利用无人机高空优势获取数据的技术。小型设备包括各种类型的相机,由于这类相机具有高清镜头,能够满足获取清晰的空中视野。无人机具有灵活、操作简单等突出优点,它能够突破空间的限制,在空中以独特的角度进行拍摄。当前使用无人机工作已经十分成熟,将航拍技术用于松林监测变得可行[2]。
文中使用大疆PHANTOM4 无人机进行航拍工作,然后运用切割的方式处理拍摄图像以增大训练集,之后使用调整结构后的VGG16 卷积神经网络模型训练得到图像与病树统计量之间的映射关系。
1 相关工作
目标计数算法能够从静态图像或动态视频中估算感兴趣对象的数量,已经被广泛应用到生产生活的各个方面。医学研究通过显微镜图像统计特定细胞的数量[3-4],安保系统利用摄像头拍摄到的视频数据统计敏感场所中的人员流动信息[5-6],林业部门使用航拍图像统计森林中各类树木的分布情况[7]。
早期的目标计数算法使用无监督学习方法,这些方法根据自相似性或运动相似性进行分组。这种完全无监督的算法计数精度通常不太理想,近年来,大量研究集中在基于监督学习的目标计数算法上。基于监督学习的目标计数算法通常分为基于检测的目标计数[8]和基于回归的目标计数[9]。
基于检测的目标计数算法首先通过检测器识别图像中的所有目标[10-11],之后统计所有检测对象的个数,得到图像中对象的总数[12]。当前大多数目标检测器分为两个工作阶段,第一阶段生成置信度图,第二阶段采用阈值化和非最大化抑制步骤来定位对应于单个实例的峰值。运用更具创造性的方法推理对象部分和实例之间的关系,以避免非最大化抑制,这些方法不仅非常耗时,而且它们仍然只适用于图像中对象数量较少的情况。也有方法假设对象趋向于均匀分布,并且背景颜色不同导致对象彼此分离,因此可以通过蒙特卡罗过程、形态分析或变分优化来定位单个实例,当均匀分布和对象彼此分离的假设成立时,这类方法提供了准确的计数结果。通常说来,基于检测的目标计数方法简单易行,但在具有大量重叠对象的场景中,基于检测的目标计数算法的性能急剧下降[13]。
与基于检测的计数算法不同,基于回归的目标计数算法是从一些全局图像特征(主要是各种特征的直方图)到对象数量的直接映射。许多机器学习算法可以实现这类回归问题[14-15]。然而,这种基于全局特征的方法仅使用某些一维统计特征进行学习,丢弃了所有可用的对象位置信息[16]。分段计数法可以看作是检测计数法和回归计数法的混合体,它们将对象分割成不同的组,然后从每个组的全局属性回归到对象的总数。
2 算法框架
文中方法是一种基于回归的目标计数算法。为了充分利用训练样本中待计数对象的位置信息,文中方法建议将原始图像对称分割为多个子区域,训练一个由子区域到区域中病树数量的回归函数,再将各区域中回归得到的病树数据相加,得到原图像中病树的数量。子区域切割方法不仅能有效利用对象的位置信息,还能够大幅降低模型的复杂程度(参数个数),避免出现过拟合,提高了算法统计病树的质量。
2.1 图像标记
为了解决病树计数问题,文中采用基于监督学习的回归方法,因此要用到标定后的图像。文中使用打点的方法在图像中标记病树,打点方法是一种很自然的计数方法,与人类日常生活中使用的计数手段一致,符合最终用户的计数习惯。
如图1 所示,在启动训练过程以前,用户使用鼠标单击图1 左图所示的病树,程序将生成右图所示的标记图。图中的标点蕴含了病树的位置信息。

图1 病树图和标记图
2.2 对称切割
式(1)所示为传统的基于回归方法优化的损失函数:
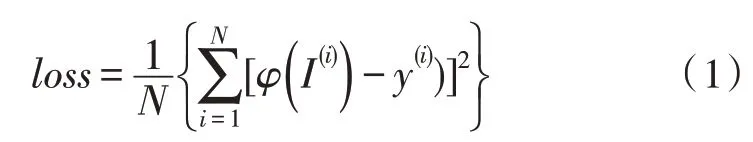
式中,N是样本个数;φ是回归函数,可以使用神经网络、支持向量机等回归的模型来实现;I(i)和y(i)分别表示第i幅图像及其中病树的数量。显然,式(1)只考虑了图像的全局特征-图像中病树的数量,但对病树出现的位置不敏感,因此,使用式(1)作为损失函数的方法不能有效利用待计数对象的位置信息。
图2 是病树位置不同的两个模拟标记图像,左边的标记图像对应的病树图像的左上角有3 棵病树,而右边的标记图像对应的病树图像的右上角有3棵病树。式(1)的损失函数不能区分这两个标记图像对应的病树图像的差别,优化得到的φ函数只要使得φ(I(i))接近3 即可,而病树位置的不同,并不能影响优化过程。也就是说,式(1)所示的损失函数只考虑了图像中的病树数量,而忽略了病树在图像中出现的位置。

图2 病树位置不同的两个模拟标记图像
为了有效利用标注图像中的位置信息,可以采用对称分割的方法,将病树图像和病树图像的标记图像在水平和垂直两个方向对称分割,图2 所示的标记图像经过一次对称分割和二次对称分割以后的标记图像如图3 所示。

图3 一次分割和二次分割后的标记图像
为采用对称分割后,相应的损失函数如式(2)所示:
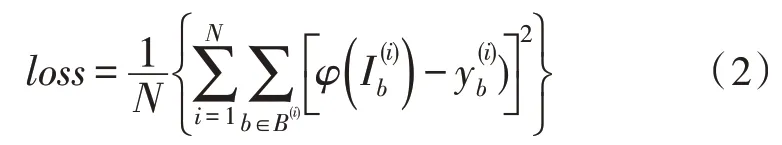
式(2)中,B(i)表示第i幅图像经过对称分割以后得到的子区域的集合,和分别表示第i幅图像的第b个子区域的图像和第b个子区域中的病树数量。
式(2)对病树的位置是敏感的,当采用图3 左列所示的一次分割的时候,病树图和标记图都被对称分为4 小块,当病树图像中的病树出现在左上角而标记图像中的标记也出现在左上角时,该幅图像的损失loss(i)为:

而当病树图像中的病树出现在右上角,而标记图像中的标记出现在左上角时,该幅图像的损失loss(i)为:
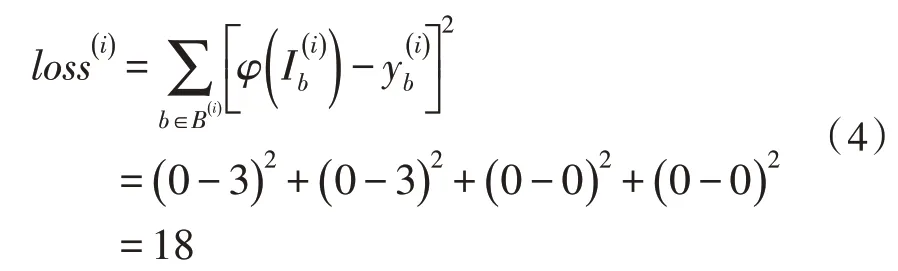
这说明当采用对称分割以及式(2)所示的损失函数时,优化算法会倾向于在标记对应的子区域内寻找图像的特征,并将其映射为子区域内的病树数量。因此,对称分割方法有利于优化算法利用标记图像中包含的病树的位置信息。
利用式(2)训练的回归函数φ能够预测子区域图像中的病树数量,其输入为分割得到的子区域图像,输出是子区域中的病树数量。第i个完整图像中的病树数量的预测值如式(5)所示:

分割方法带来的另一个好处是减少了过拟合风险。一方面,分割方法使得回归函数φ的输入从整个图像变为图像的子区域,输入规模的下降导致模型参数数量的减少;另一方面,分割也导致可用标记样本数量增加,从而减少过拟合发生的风险。
2.3 网络结构
图4 所示为修改后的VGG16 卷积网络建模,它的回归函数为φ。在原始的VGG16 模型上,改变了第一层的输入尺寸,并在最后增加了一个flatten 层和两个全连接层。卷积层用于病树图特征的提取,全连接层用于建模特征到病树数量的回归函数。卷积层和池化层构成模型的前5 个模块。最后三层第一层用于将提取的特征展开为一维数据,第二层是将提取的数据大小压缩至1×1 024;最后一层输出图像中病树的统计数量。
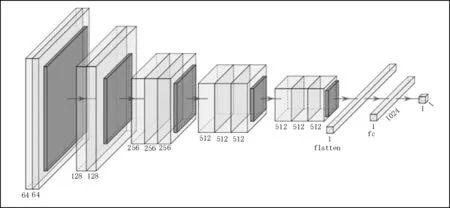
图4 改进后VGG16模型结构图
当输入模型的图像分辨率为114×152时,模型摘要数据如图5所示,模型一共使用21 008 193个参数。

图5 神经网络模型摘要图
3 实 验
该研究通过对称分割图像来利用标记图像中的位置信息,提高了目标计数算法的统计准确率。为了验证算法的有效性,使用python 语言和tensorflow机器学习库实现了基于对称分割的计数算法,实验使用40 张病树图像作为训练集,训练集总计含有505 棵病树,平均每张图像含有12.625 棵病树。实验使用了额外30 张图像作为测试集检测训练效果,测试集含有608 棵病树,平均每张图像含有20.267 棵病树。所有图像的分辨率为456×608。使用参数γ控制对称分割的次数,比如当γ=0 时,输入神经网络的分辨率为456×608 的原始图像,当γ=2 时,表示在水平和垂直方向做了两次分割,得到16 个分别率为114×152 的子图像。
实验计算了在不同γ值下,预测的病树数量与真实病树数量y(i)绝对误差的平均值MAE和绝对误差方差VAR。MAE的计算公式如式(6)所示:
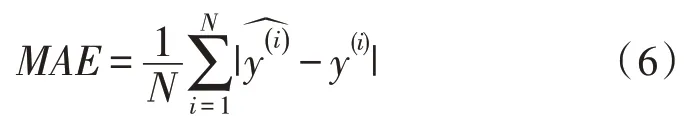
VAR的计算公式如式(7)所示:
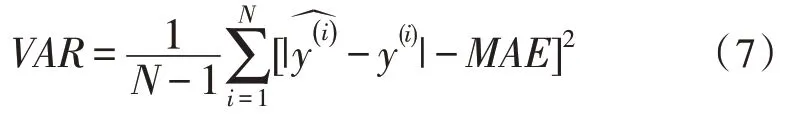
不同分割次数γ值下MAE和VAR的计算结果如表1 所示。从表1 中可以看出,相对于不分割的方法(γ=0),对称分割方法(γ≥1)能够有效降低病树计数中的绝对平均错误和绝对错误的方差,且随着分割次数的增加,绝对平均错误和绝对错误的方差会逐渐减少,但当分割次数达到一定的数量(γ=5)时,绝对平均错误和绝对错误的方差开始增加,这可能是因为分割次数太大,单个子图像不能包含一个完整的病树,导致特征提取失败。总之,实验结果表明,适当对称分割病树图像和标定图像能够提高计数算法的准确率和稳定性。
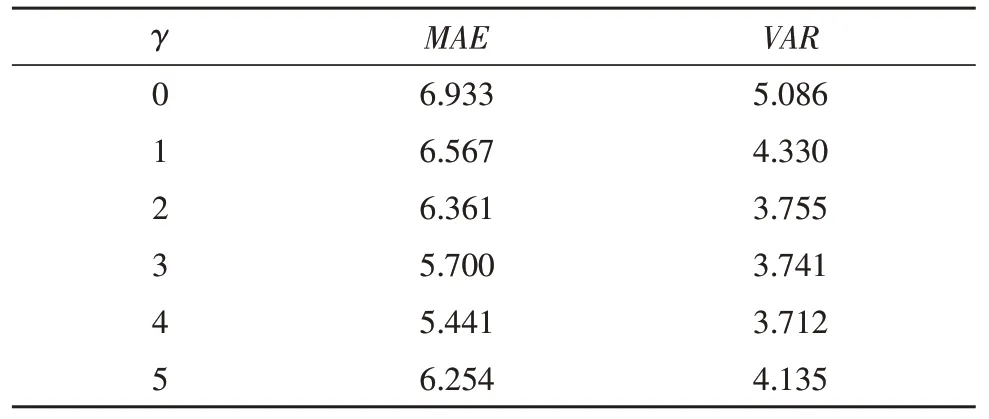
表1 不同分割次数γ 值下MAE和VAR的计算结果
4 结束语
文中提出了一种基于对称分割的计数算法,实现了松材线虫病树的统计。一方面,通过对称的分割能够有效利用病树标记图像中的位置信息,提高计数算法的准确度。另一方面,对称分割能够减少输入图像的尺寸,降低模型的复杂程度,保证在训练样本较少的情形下,能够提高算法统计的准确率。这样的优点使得对称分割方法特别适合情况复杂多变的森林病虫害监测场景。

