人体动作识别中的惯性传感器位置校正算法

赵 琰, 郭 明, 孙建强, 邱建龙

(临沂大学自动化与电气工程学院,山东临沂 276005)

1 引言

人体动作识别是通过各种传感器设备对人体动作数据进行采集和处理,并使用合适的机器学习算法,以实现自动识别各种人体动作类型.它在人机交互[1]、医疗康复[2-3]等领域都有广泛的应用.

传统的人体动作识别多数使用基于视觉的方法,主要通过拍摄身体轮廓和动作轨迹,得到相关运动特征参数,从而识别人体动作.视觉技术可以快速获取大量信息以便于计算机的自动处理,但是不适合长时间跟踪记录.且受光照、遮挡、背景环境等因素的影响,容易降低图像分割精度,从而影响最终识别效果.为了更好地实现对人体动作的监测,各种各样微型化、低成本、高性能的惯性传感器被广泛应用.用于人体动作识别的惯性传感器系统主要利用加速度计、陀螺仪等多个惯性传感器通过近距离无线网络技术组网,对人体动作进行监测[4].例如,在文献[5]中,使用智能手机作为数据采集平台,采集静止、行走、跑步、上楼、下楼和骑行6种运动状态的加速度和角速度数据,并提出并联卷积神经网络(PCNN)作为分类器.在文献[6]中,使用4个惯性传感器测量下肢截肢患者穿戴假肢行走的角速度信号,通过比较假肢与完整肢体步幅的相似性,进而对患者作出康复治疗.在文献[7]中,使用三轴加速度计、陀螺仪、磁力计数据判断不同年龄段的成年人在步行时的表面状况和年龄差异.在进一步研究后,可应用于预防和干预老年人的跌倒事件.在文献[8]中,提出一种基于稀疏信号的方法,使得可穿戴传感器不必被限制在固定的身体位置,并且对7个人体位置和14类人体活动进行测试和识别.在文献[9]中,提出自适应贝叶斯推理系统,这是一种基于可穿戴传感器的步行活动和步态事件的识别和预测方法.实验表明此系统能够适用于可穿戴传感器日常活动的智能识别.

利用惯性传感器采集人体动作数据时,用户通常需要重新穿戴惯性传感器,却很难保证每次都将其固定在同一位置.而惯性传感器测量的加速度、角速度、角度等数据与其固定位置有直接的关系,当固定位置与预设位置发生偏差时,就会降低动作的识别精度[10].所以如何解决惯性传感器的位置校正问题是值得思考的.在文献[11]中,提出一种在人体动作识别中提高加速度计安装误差鲁棒性的方法,使用Gram-Schmidt正交化计算变换矩阵,把三轴加速度数据转换到空间坐标系中,并采用截止频率为10 Hz 的低通滤波器消除传感器的方位误差.不过该方法计算量比较大,不适合处理实时运动信号,对滤波器的选择也有较高的要求.在文献[12]中,为消除原始惯性传感器数据中关于传感器方向的影响,提出基于启发式和基于奇异值分解的两种变换方式.在预处理阶段把时域传感器数据进行简单变换,转换后的数据独立于多轴传感器的绝对方向.虽然该方法取得了很好的分类效果,但是转换后数据量的倍增加重了数据处理的负担.为避免校正过程中计算量大、变换复杂的问题,本文将矩阵旋转变换原理应用到惯性传感器位置校正中,只需将三维空间坐标系进行简单的旋转变换而非改变原有坐标系类型.另外旋转变换矩阵是通过一小段基准数据得到的,避免使用全部动作数据进行求解.

本文搭建了一个基于惯性传感器系统的人体动作数据采集平台,通过绑定在两侧手腕处的两个惯性传感器采集所规定的8个实验动作数据.针对每次数据采集时惯性传感器固定位置发生变化的情况,提出一种基于旋转矩阵的惯性传感器位置校正方法对测试数据进行校正,测试数据校正的好坏直接影响最终的识别精度.接着使用滑动窗口对校正后的数据进行特征提取后,为了保证实验动作的有效识别,提出了加权BP神经网络模型作为分类器对实验动作进行识别.

2 提出的模型算法

2.1 旋转变换矩阵

在实际环境中,利用惯性传感器监测人体健康时,受用户身高、体重、穿戴方式等因素的影响,用户穿戴惯性传感器时会导致传感器中惯性测量单元的位置发生变化,就会导致所采集的测试动作数据与训练动作数据在方向上存在一定的偏差,进而严重影响识别系统的精度.因此,本文提出了一种基于旋转变换矩阵实现惯性传感器位置校正的人体动作识别方法.首先分别采集训练数据和测试数据的基准数据,然后利用两组基准数据,借助矩阵旋转变换原理求出校正前与校正后数据的旋转变换矩阵,实现测试数据的校正.

假设在测试者身上一共绑定了m个传感器节点.在采集训练数据时,如图1(a)所示,先令测试者静止t秒,此时传感器采集的数据作为训练数据的基准数据,设每个传感器节点采集的训练数据基准矩阵为Ai(i=1,2,··· ,m).类似地,在采集测试数据时,如图1(b)所示,也先令测试者静止t秒,则此时传感器采集的数据为测试数据的基准数据.设每个传感器采集的测试数据基准矩阵为Bi(i=1,2,··· ,m).由于佩戴在人体上的m个传感器节点之间是彼此独立的,所以训练数据基准矩阵Ai之间是彼此独立的,测试数据基准矩阵Bi之间也都是相互独立的.

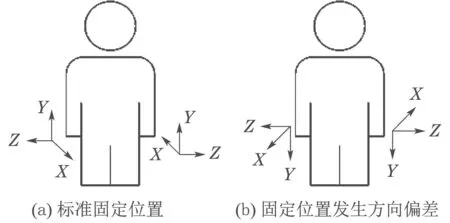
图1 固定在手腕上的惯性传感器Fig.1 Inertia sensors fixed to wrist

根据机器人学相关理论,对于每一个传感器节点i(i=1,2,··· ,m),训练数据基准矩阵Ai都可以通过旋转变换矩阵Ri得到测试数据基准矩阵Bi.这里假设传感器节点不会发生平移(由于一般用以实现人体动作识别的惯性传感器节点测量精度不高,因此本文忽略位移产生的影响).本文使用内旋方法求取相应的旋转变换矩阵,内旋是指每次旋转围绕的轴是上次旋转之后坐标系的某个轴,旋转角度的正负也遵循右手坐标系的约定.设第i个传感器的初始坐标系如图2(a)所示.先绕X坐标轴旋转a,再绕着Y坐标轴旋转b,最后绕着Z坐标轴旋转c,得到如图2(b)所示的传感器位置.则整个旋转变换矩阵Ri表示为

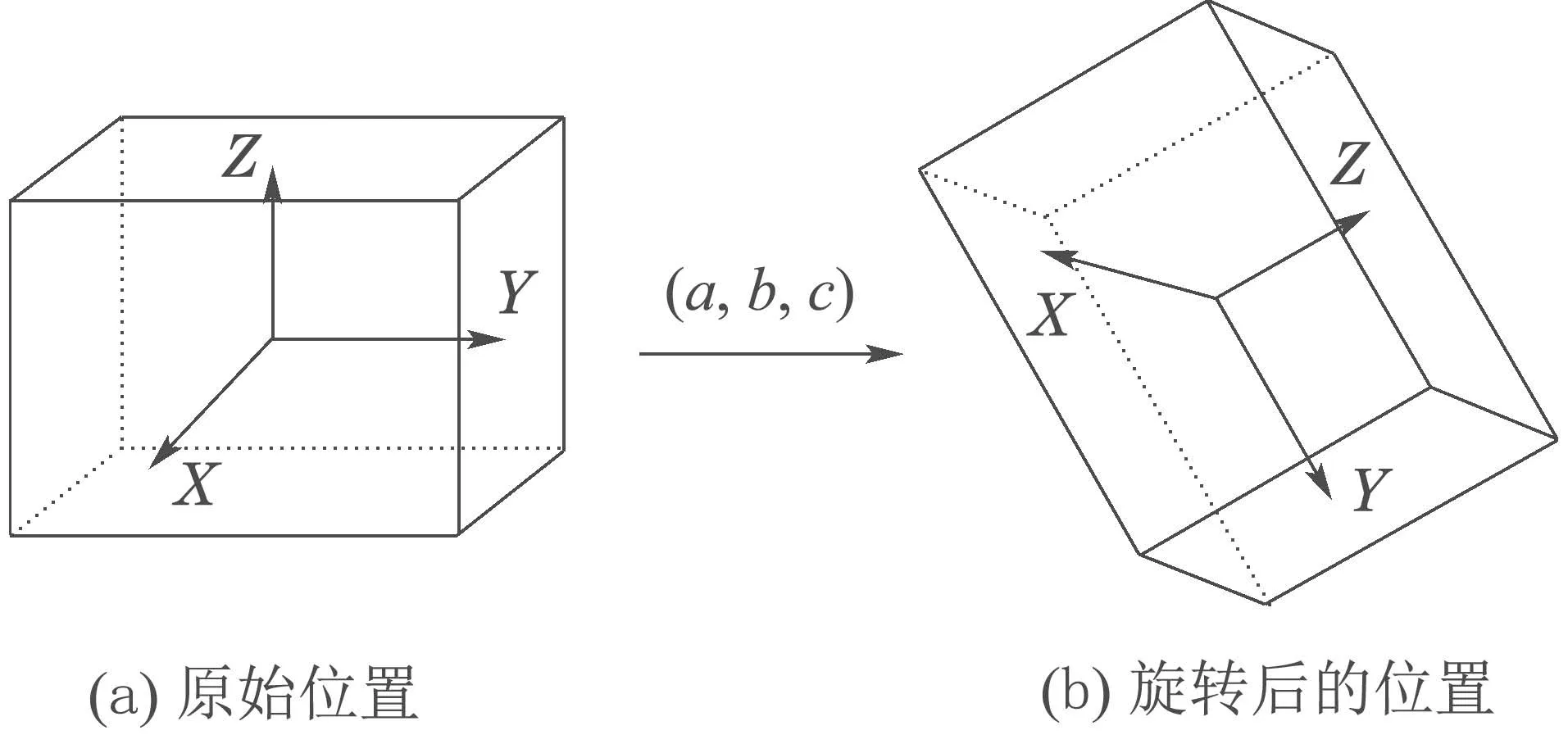
图2 传感器坐标系发生旋转变化Fig.2 Rotation of sensor coordinate system

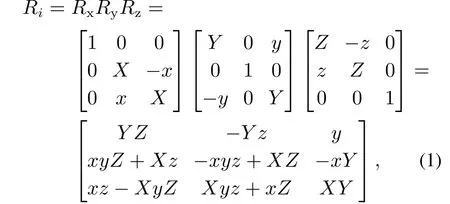
其中:x=sina,y=sinb,z=sinc,X=cosa,Y=cosb,Z=cosc.

对于每一个传感器节点i,所采集的测试数据矩阵Bi和校正后的测试数据矩阵˜Bi的关系可表示为

2.2 加权BP神经网络

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络,在人体动作识别中应用广泛[13-14].BP神经网络结构由输入层、输出层、隐含层组成,其原理是将预测值y和真实值Z的误差δ通过网络模型进行反向传播,并且通过多次迭代,使用梯度下降法不断地对网络中所有的连接权重进行调整,直至误差小于预设值,如图3所示.

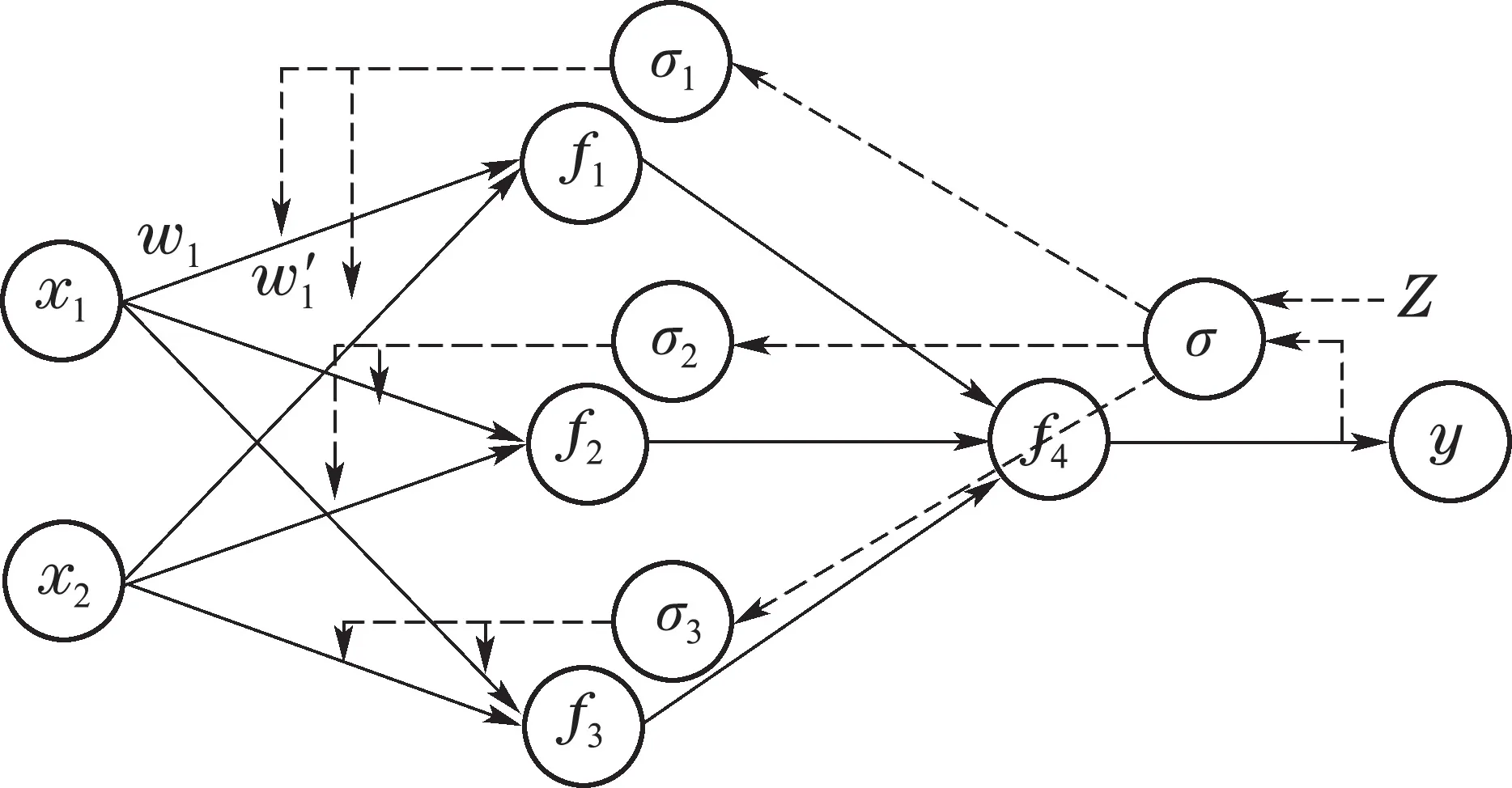
图3 BP神经网络原理图Fig.3 Schematic diagram of BP neural network

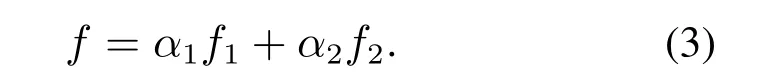
从训练集中随机选择30%的数据作为参数选择的训练数据.采用两个常见的激活函数,如sigmoid函数、tanh函数以及Relu函数等分别作为该网络的激活函数进行分类识别,令最终识别准确率为θi,i=1,2,则式(4)中的权重可表示为

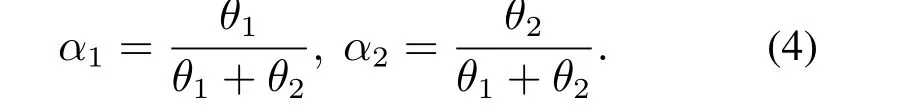
另外,选择均方差作为损失函数,训练精度设置为0.001,初始学习率设置为0.01,这样既可以保证快速顺利找到损失函数的最小值,又不会导致反复震荡[15].

3 动作数据采集平台

3.1 实验平台

本文搭建实验平台采集人体动作数据,该平台由惯性传感器、蓝牙接收器和上位机组成.每个传感器节点内置一个MPU9250 三轴加速度计,量程为[−16 g,16 g],精度为0.01 g.将两个传感器分别固定在被测者的两侧手腕处,采集的动作数据通过无线传输到蓝牙接收器,电脑读取接收器中的数据并进行保存.

3.2 实验动作的数据采集

本实验招募到男女共12名被测者用于动作数据采集,年龄在23-25岁且身体健康.在实验室环境内完成伸出大拇指、招手、双手交叉、搓手、双臂交叉、双手抱头、双手叉腰、双臂张开8个动作的数据采集,用M1-M8表示,如图4所示.加速度计的采样频率设置为50 Hz,并且要求被测者静止一段时间,随后按照各自的行为习惯,在两分钟内重复完成每个动作.

图4 实验动作图例Fig.4 Legend of experimental actions

从招募的12名被测者中随机挑选出10人用于采集训练数据,惯性传感器按照标准固定位置固定在被测者手腕上,如图5(a)所示.其余2人用于采集测试数据,传感器分别按照图5(b)和图5(c)两种固定位置固定在被测者手腕上,令采集得到的测试数据为Q1,Q2.

图6是原始动作数据中传感器节点2(固定于左侧手腕)分别按照图5(a)-(c)3种不同固定位置下所采集的M1动作的部分三轴加速度数据,每秒采集50组数据,横轴为样本点数量,纵轴为加速度计的输出值.

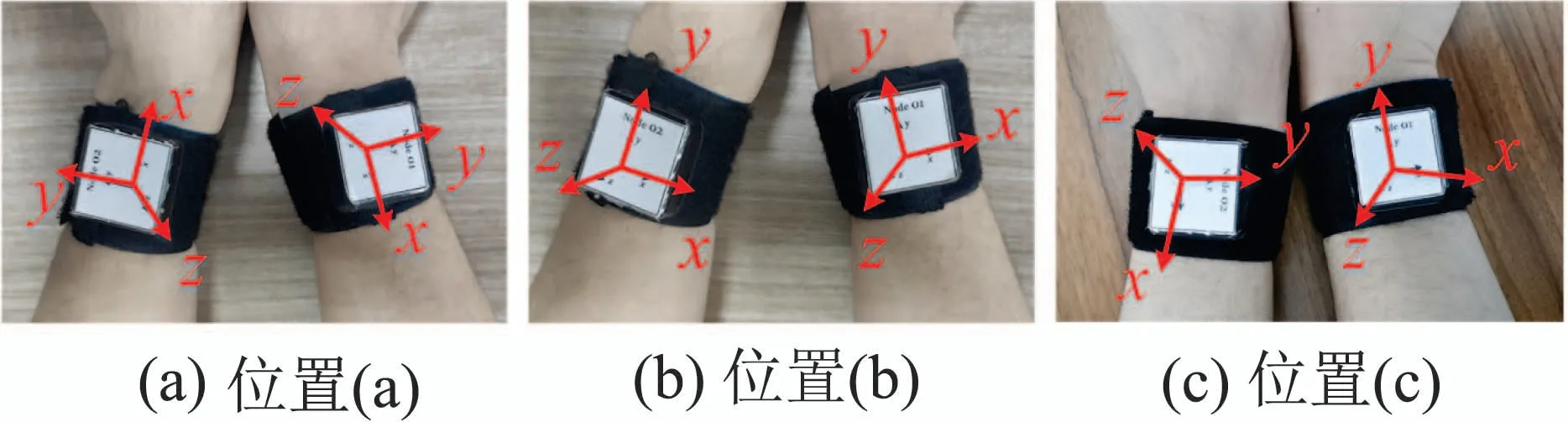
图5 3种惯性传感器固定位置Fig.5 Three fixed positions of inertial sensors

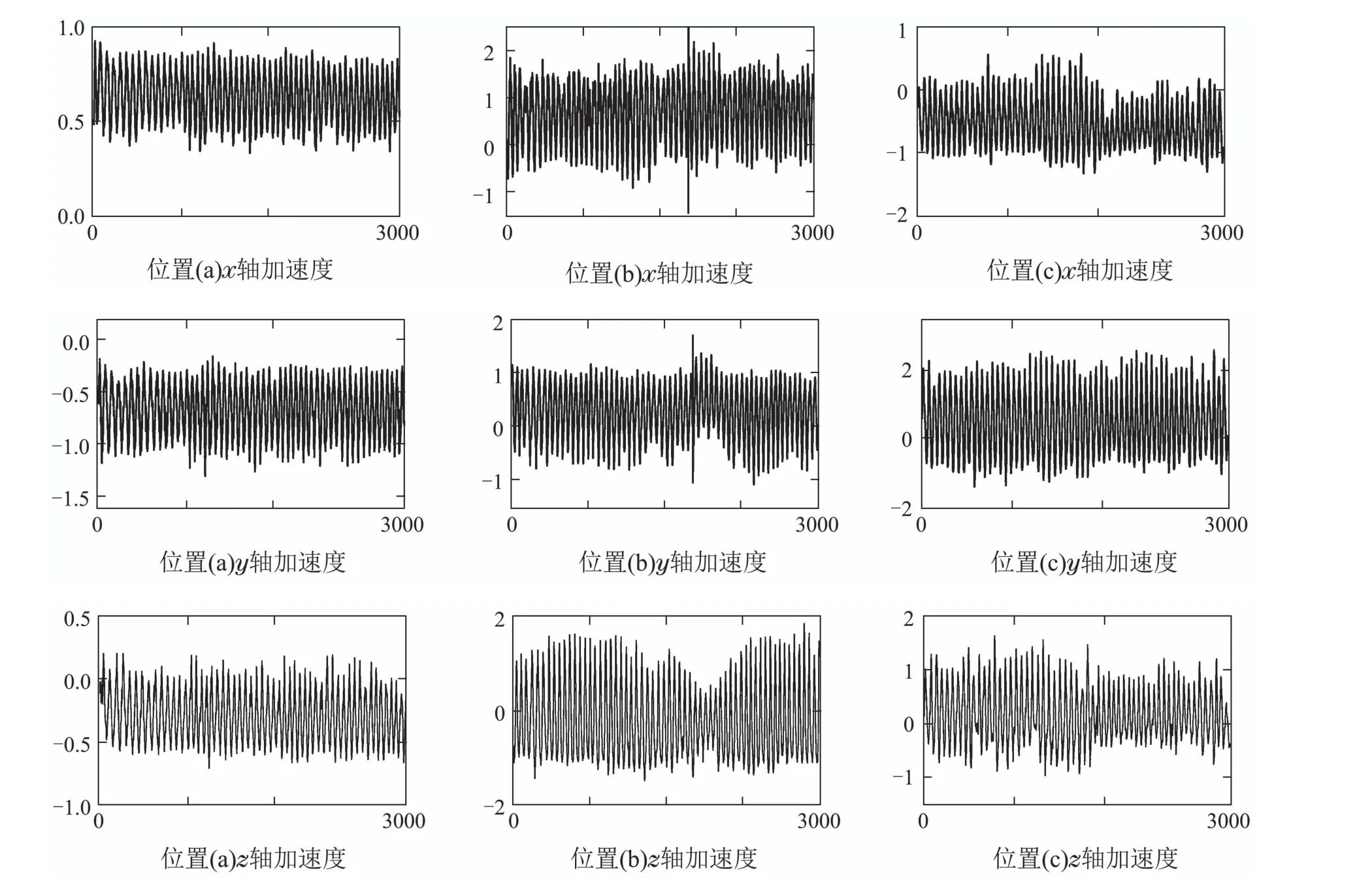
图6 校正前的原始加速度数据Fig.6 Raw acceleration data before correction

4 实验结果与分析

4.1 动作数据校正

基准数据为被测者穿戴惯性传感器保持静止状态时所记录的动作数据.图7为被测者在3种固定位置下两个传感器节点所采集的基准数据Pij,如P12表示传感器节点2按照第1种固定位置(a)的所采集的训练基准数据,可以看出不同传感器固定位置的基准数据的初始值有明显的差异.通过旋转矩阵变换原理可以得到4个三维旋转矩阵(2个惯性传感器×2种固定位置),并利用旋转矩阵将测试数据Q1,Q2进行校正,得到校正后的动作数据,如图8所示.

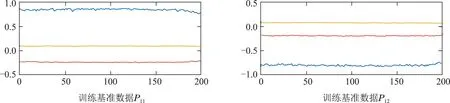
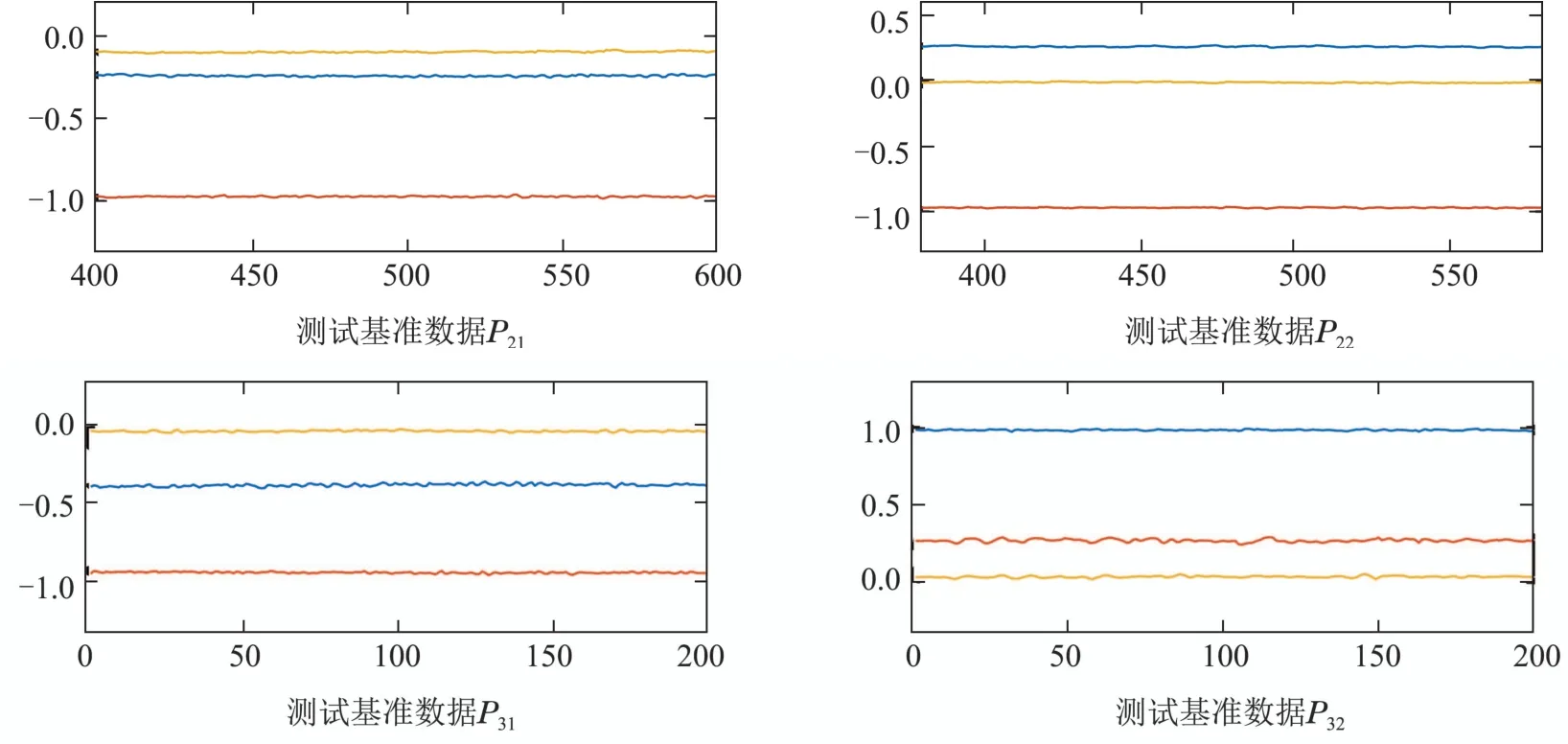
图7 基准数据Fig.7 Benchmark data

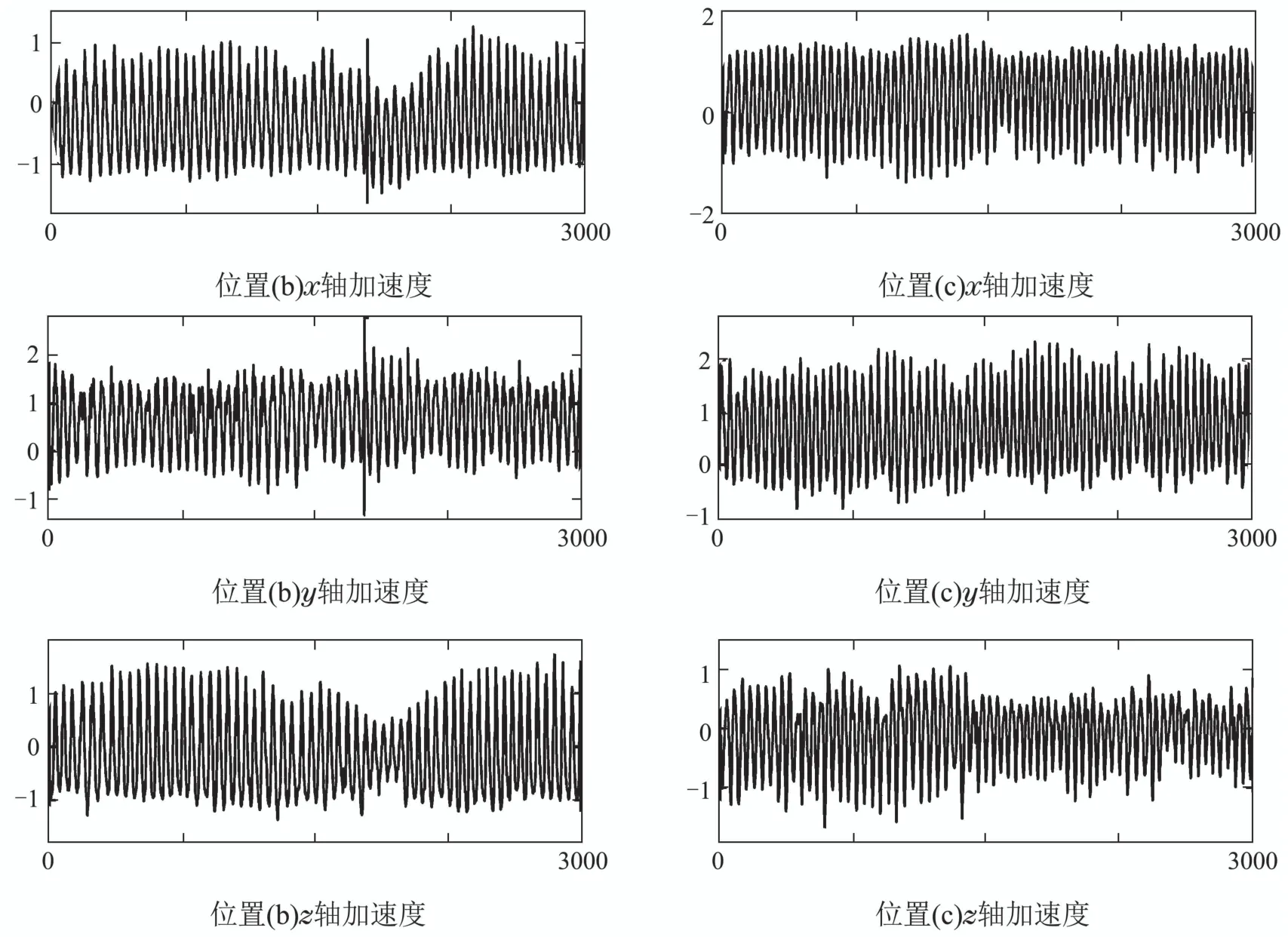
图8 经过旋转矩阵处理后的加速度数据Fig.8 Acceleration data processed by rotation matrix

4.2 动作数据特征提取

原始数据中会存在许多噪音,而且往往是不可避免的,这会对动作识别结果产生很大的影响.噪音可能是传感器与身体碰撞造成的,也可能是受到传输滞后的影响造成的.本文选用卡尔曼滤波[16]的方法处理异常值.然后使用滑动窗口方法把清洗后的数据分割成等长的数据窗,这样可以更好地对较长的数据进行分析.将窗口长度设为100个样本点(约2 s),为了避免两个窗口相邻处的数据丢失,将两个相邻窗口的重复率设为50%,即窗口间隔为50个样本点(约1 s).对每个窗口内的数据进行特征提取,选定时域、频域特征共6个,如表1所示.

表1 特征提取Table 1 Feature extraction

4.3 实验结果分析

为了确保实验结果的有效性,本文采用十折交叉验证的方法对分类模型进行训练,将处理完的训练集数据随机地平均分为10份,将其中9份轮流作为训练数据,另外的1份作为验证数据,一共迭代10次,最终识别结果为10次迭代结果的平均值.使用准确率作为模型的评价指标,可描述为被正确分类样本数占所有样本数的比例.

首先讨论不同的传感器固定位置对识别准确率的影响.将3名被测者分别按照图9所示的3种传感器固定位置穿戴传感器采集的测试数据作为测试集分别进行测试,其他的识别步骤保持一致.如图10所示,当传感器固定位置为(a)时,准确率为97.16%.当传感器固定位置为(b)时,准确率为18.09%.固定位置为(c)时,准确率为31.59%.这说明传感器的固定位置确实会影响人体动作的识别效果.

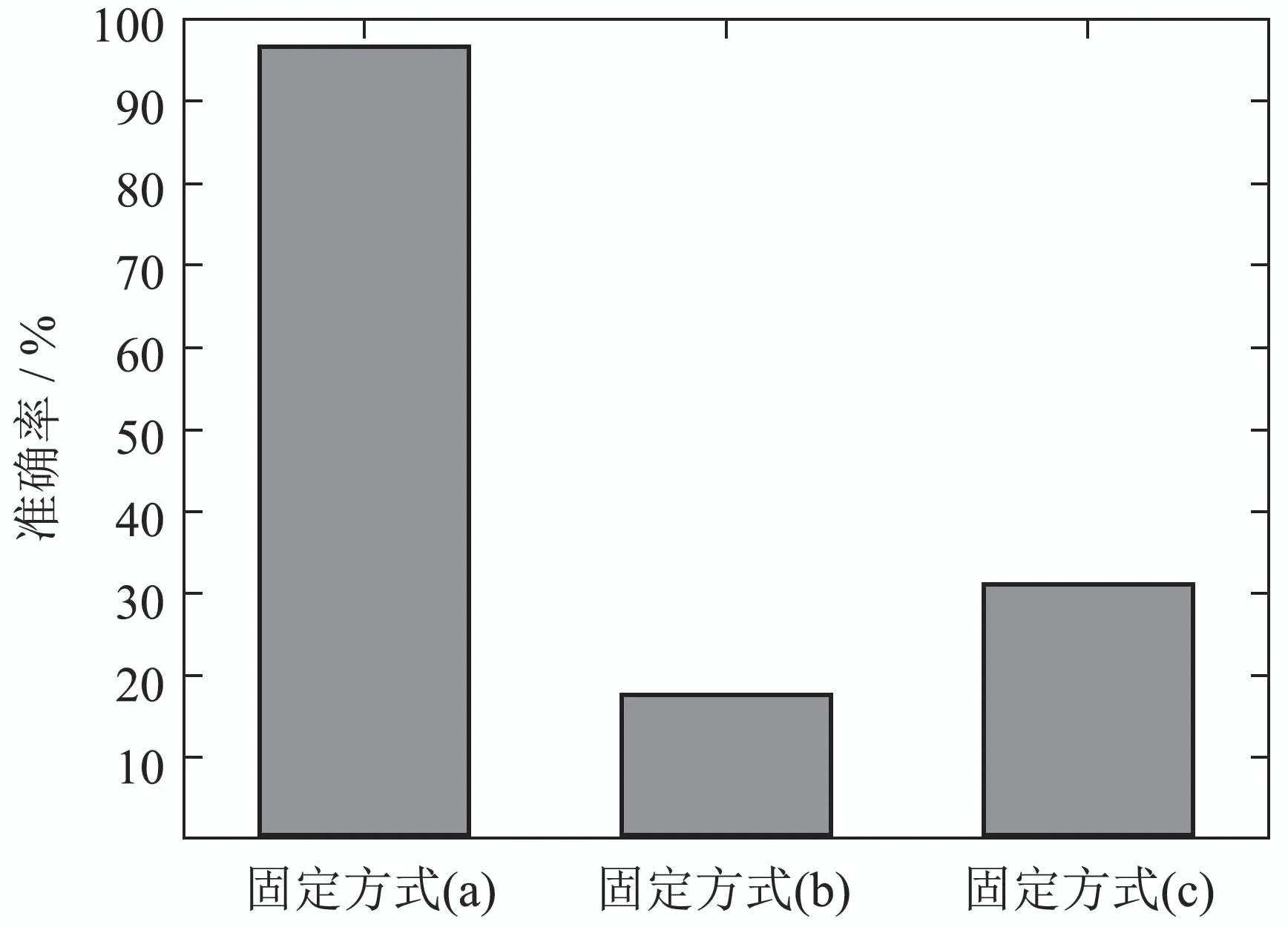
图9 3种传感器固定位置对识别率的影响Fig.9 The influence of three fixed positions of sensors on accuracy

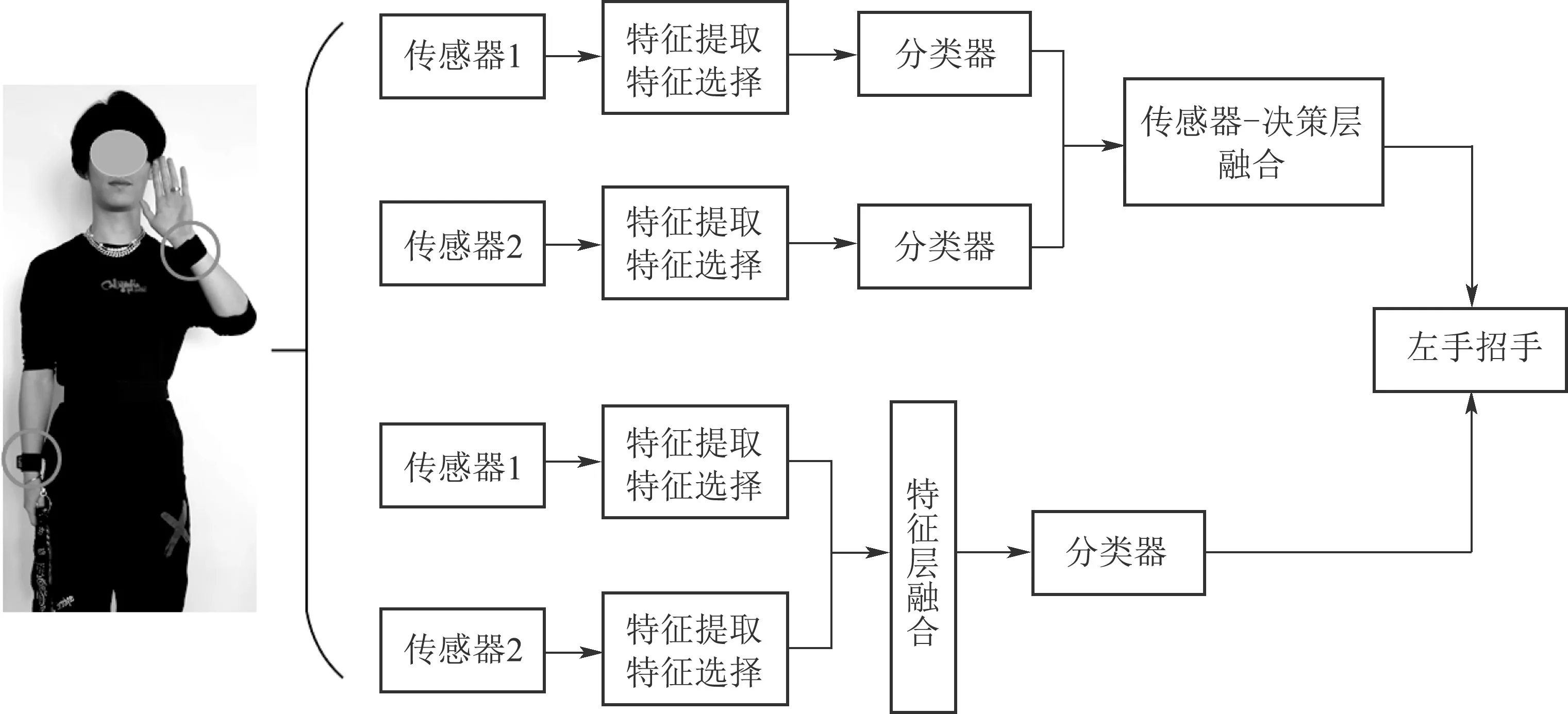
图10 特征层融合和传感器-决策层融合流程图Fig.10 Flow diagram of feature level fusion and sensor-decision level fusion

同时,本文针对识别过程中不同的数据融合方式对识别结果的影响,主要研究了特征层融合和传感器-决策层融合.特征层融合是对每个传感器采集的动作数据的多类特征进行提取,然后联合在一起形成一个统一的特征向量[17],再对其进行特征选择.传感器-决策层融合是指每个传感器都具有独立的数据处理能力,包括动作数据的特征选择和对动作类型的分类识别,然后再对每个传感器的识别结果进行融合,得到最终预测结果.

接下来验证旋转变换矩阵的有效性.使用旋转矩阵对测试数据Q1,Q2进行校正,并且讨论了传感器固定位置为(b)(c)两种情况下,不同数据融合方式对识别准确率的影响.

第1种情况为传感器固定位置为(b)时,8个动作的识别准确率如图11所示.可以看出使用特征层融合时,‘双手抱头’的识别准确率最高,达到了100%,其次是‘伸出大拇指’,达到了98.90%,‘双手交叉’的识别准确率最低,仅为40.00%,平均准确率为84.25%.在传感器-决策层融合时,‘双手抱头’的识别准确率最高为100%,其次是‘伸出大拇指’,识别率为98.9%,识别率最低的动作是‘双手交叉’,识别率为33.75%,另外,‘招手’的识别率也较差为53.49%,平均准确率为82.7%.

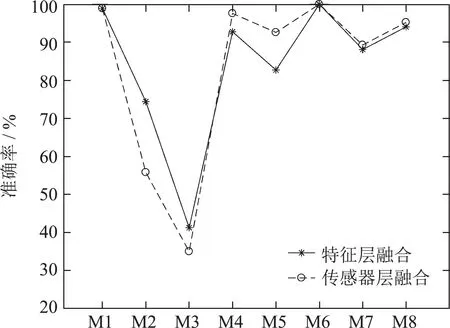
图11 传感器位于固定位置(b)时两种数据融合方法对比Fig.11 Comparison of two data fusion methods for sensors in fixed position(b)

对于整体识别准确率高但单一动作识别率低的情况,使用混淆矩阵进可以清晰地看出预测值和真实值的分布.它每一行表示样本的真实类别,每一行的总数表示该类别的实例样本的数量,每一列表示样本的预测类别,每一列的总数表示预测为该类别的样本数量,每一列中的数值表示实际样本被预测为该类的数量.图12给出了固定位置(b)在特征层融合时的混淆矩阵.通过混淆矩阵能够很清楚的看出,‘双手交叉’的80个测试样本中,有48个样本被错误分类,其中有27个样本被误分为‘搓手’,有16个样本被误分为‘双臂交叉’,有5个样本被误分为‘双手抱头’.通过图13所示的传感器-决策层融合时混淆矩阵,‘双手交叉’被误分类的情况与上述类似,另外‘招手’的86个样本中的40个样本被误分为‘双手交叉’.

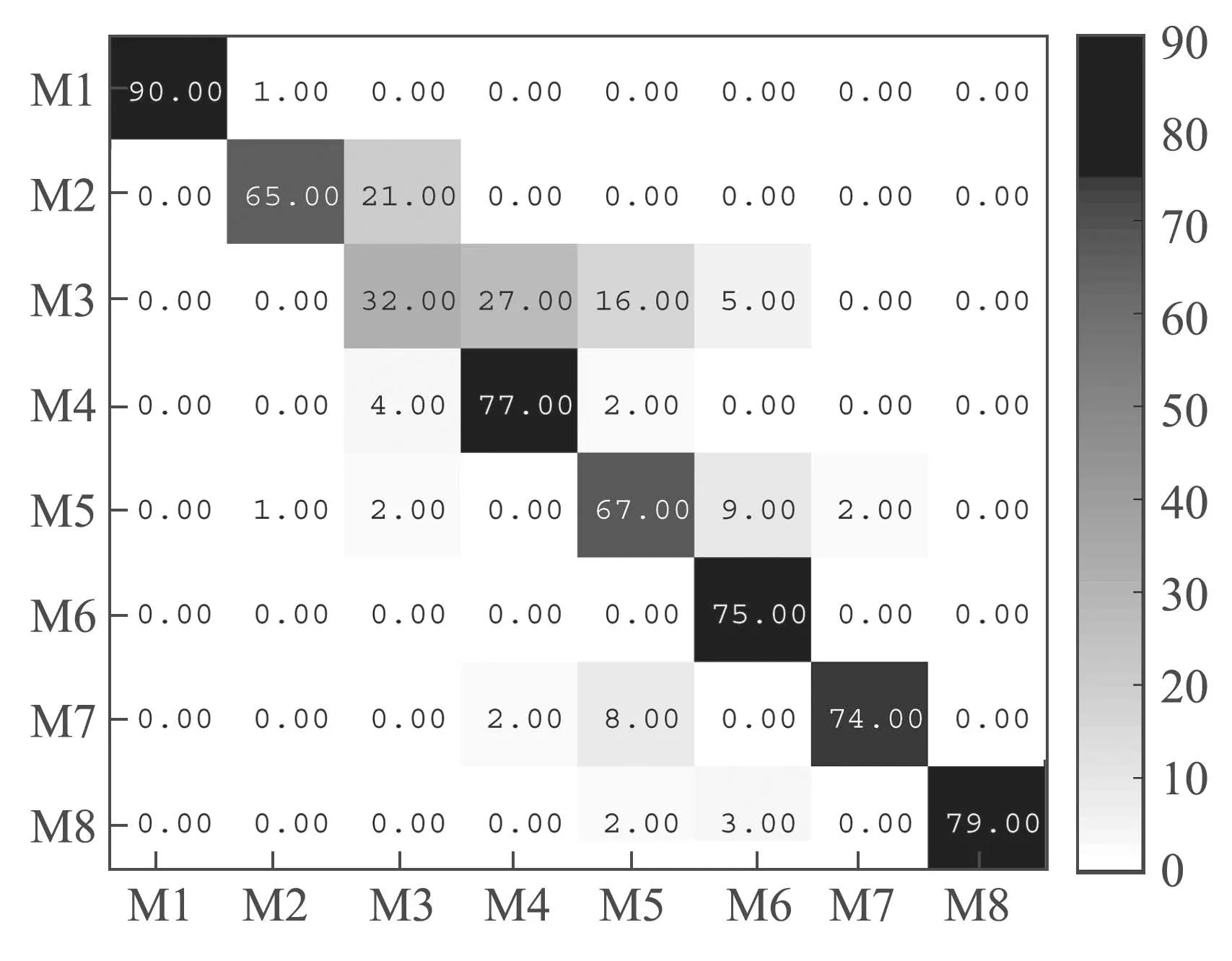
图12 传感器固定方式(b)对特征层融合的混淆矩阵Fig.12 Confusion matrix of sensor fixed position(b)on feature layer fusion

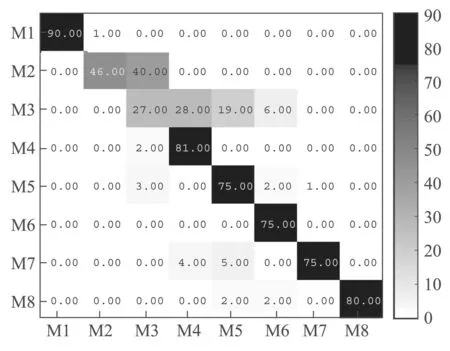
图13 传感器固定方式(b)对传感器-决策层融合的混淆矩阵Fig.13 Confusion matrix of sensor fixed position(b)on sensor-decision level fusion

第2种情况为传感器位置为(c)时,动作的识别准确率如图14所示.可以看出在特征层融合时,‘双臂交叉’、‘双手叉腰’、‘双手抱头’的识别准确率都达到了100%,其次是‘双臂张开’,准确率为98.59%,‘伸出大拇指’的识别准确率最低,仅为41.79%,平均准确率为85.94%.在传感器-决策层融合时,‘双臂交叉’、‘双手叉腰’、‘双臂张开’的识别准确率也为100%,其次是‘双手叉腰’,识别率为96.25%,识别率最低的动作是‘双手交叉’,识别率为45.00%,另外,‘伸出大拇指’的识别率也较低,为46.27%,平均准确率为81.08%.

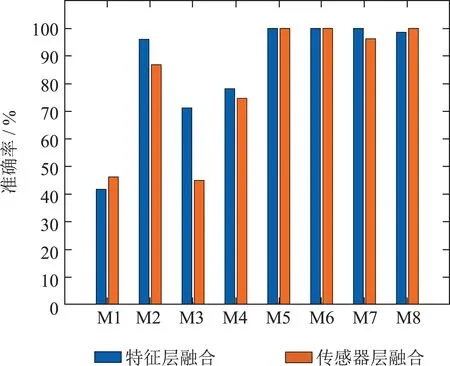
图14 传感器固定位置(c)下两种数据融合方法对比Fig.14 Comparison of two data fusion methods for sensors in fixed position(c)

图15给出了固定位置(c)在特征层融合时的混淆矩阵.可以看出‘伸出大拇指’的67个测试样本中,有39个样本被错误分类为‘招手’,‘双手交叉’中有19个样本被误分为‘双臂交叉’,有4个样本被误分为‘双手抱头’.而通过图16的混淆矩阵,‘伸出大拇指’的67个测试样本中,有36个样本被错误分类为’招手’,‘双手交叉’的80个样本中有44个样本被错误分类,其中有36个样本被误分为‘搓手’,有8个样本被误分为‘双臂交叉’.

图15 传感器固定方式(c)下特征层融合的混淆矩阵Fig.15 Confusion matrix of sensor fixed position(c)on feature layer fusion

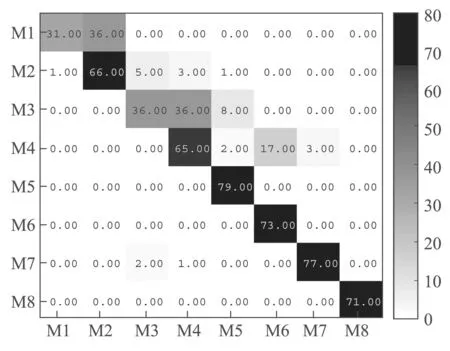
图16 传感器固定方式(c)下传感器-决策层融合的混淆矩阵Fig.16 Confusion matrix of sensor fixed position(c)on sensor-decision level fusion

通过对比两组实验可以发现,本文所进行的动作识别中特征层融合的整体准确率是高于传感器-决策层融合的.其主要原因是在传感器-决策层融合中,每个传感器相互独立用于分类任务,而忽略了各传感器数据之间的联系.不过,这种融合方式可以灵活选取传感器结果,提高系统的容错性,并降低了融合信息计算量.另外对于实验中出现了某一动作识别率低但整体识别率高的情况,通过混淆矩阵可以看出其主要原因是由动作和动作之间的相似性造成的,还有可能受到手动提取特征的局限性导致固定特征不能充分反映每个不同的动作类型.

5 结论

本文主要研究了人体动作识别中惯性传感器的位置校正问题,通过建立的实验平台中固定在被测者两侧手腕处的惯性传感器采集人体动作数据,通过矩阵旋转变换原理校正由不同惯性传感器固定位置所采集的动作数据,对校正数据提取特征处理后采用加权BP神经网络对实验动作进行分类.从实验结果可以发现,数据校正前后的识别效果提升明显.在未来工作中,将考虑围绕以下方面进行研究.手动提取的特征虽然是直观有效的,但是这可能会忽略一些有用的特征,可以使用卷积神经网络自动提取特征;另外,随着智能手机计算能力提升和使用普及,它不仅能集成多种传感器还拥有较大的存储量.并且相比于可穿戴惯性传感器具有不需要增加设备、不妨碍正常活动的优点,考虑使用智能手机或者手环代替传感器完成数据采集工作.