标准型半潜生活平台非对称系泊设计

蔡 灵，柏洪涛

（1. 南通中远海运船务工程有限公司 海工与新能源研发中心，江苏南通 226006；2. 江苏科技大学 船舶与海洋工程学院，江苏镇江 212003）

0 引言

标准型半潜生活平台的主要功能是辅助其他钻井类或生产类平台，为作业人员提供生活居住设施，或为其他平台储运物资补给。标准型半潜生活平台需要在世界不同海域进行平台自身系泊定位，以及与其他不同类型的生产平台进行联合靠泊等不同形式的海上作业。标准型半潜生活平台的系泊系统应满足相应的作业定位要求，并且还需要适应不同海域的作业水深和海域环境条件。标准型半潜生活平台系泊系统为了避开生产平台的系泊系统和复杂的海底管线，一般采用非对称的系泊形式。本文采用时域全耦合分析方法对平台运动响应进行分析，并对锚泊系统进行设计。

1 平台基本参数

标准型半潜式生活平台由4个方形立柱和2个浮筒组成，采用8点锚泊系统，平台侧视图及局部坐标系定义见图1，标准型平台主尺度取值情况见表1。

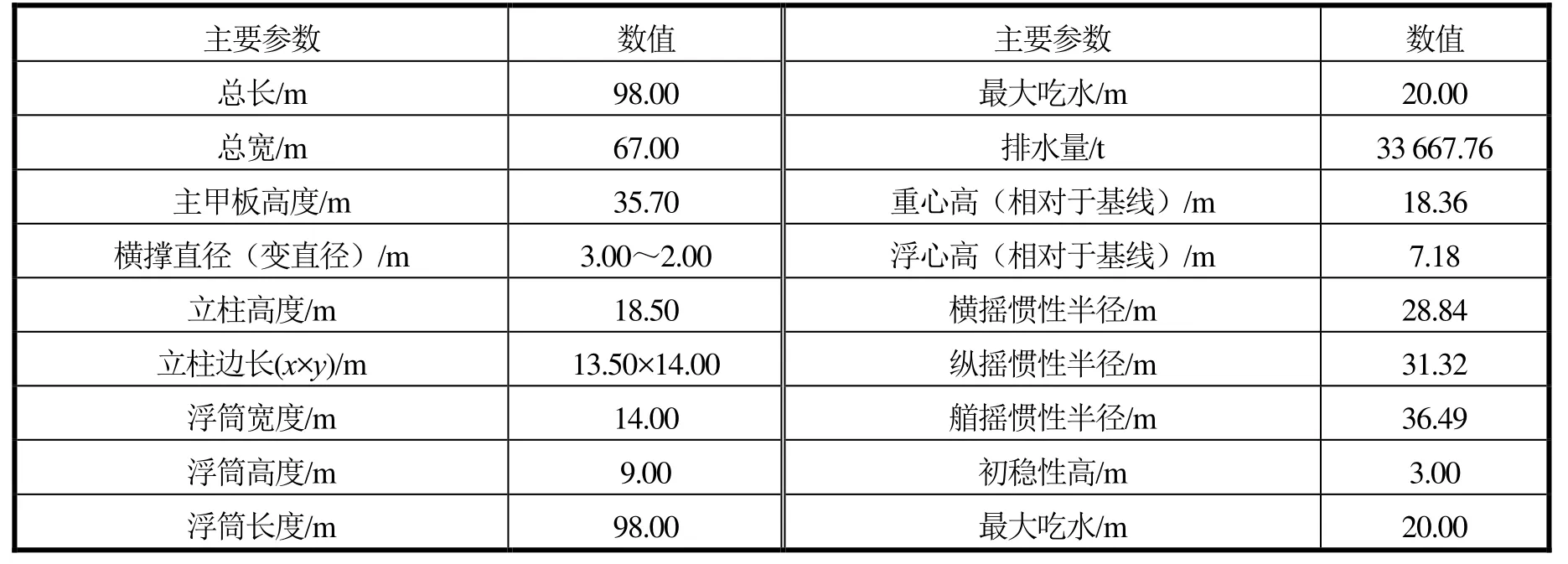
表1 标准型平台主尺度

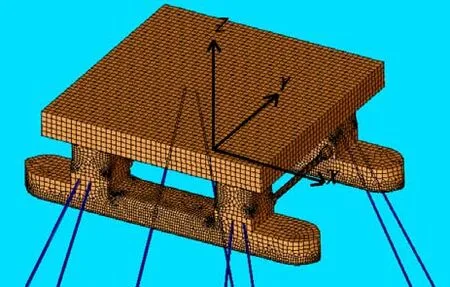
图1 标准型半潜式生活平台建模图

1.2 研究区域环境条件基本参数

1.2.1 工作水深

标准型半潜生活平台所处海域工作水深为1 500 m。

1.2.2 流荷载

标准型半潜生活平台的试验流速

V

及模拟海况见表2。

表2 试验流速（全尺度）

标准型半潜生活平台受到的流载荷(

F

,

F

)及作用中心(

C

,

C

,

C

)通过风洞试验数据计算得到（见表3）。由于标准型平台呈轴对称，故流向取为0°、45°和90°其作用中心坐标相对于平台基线定义。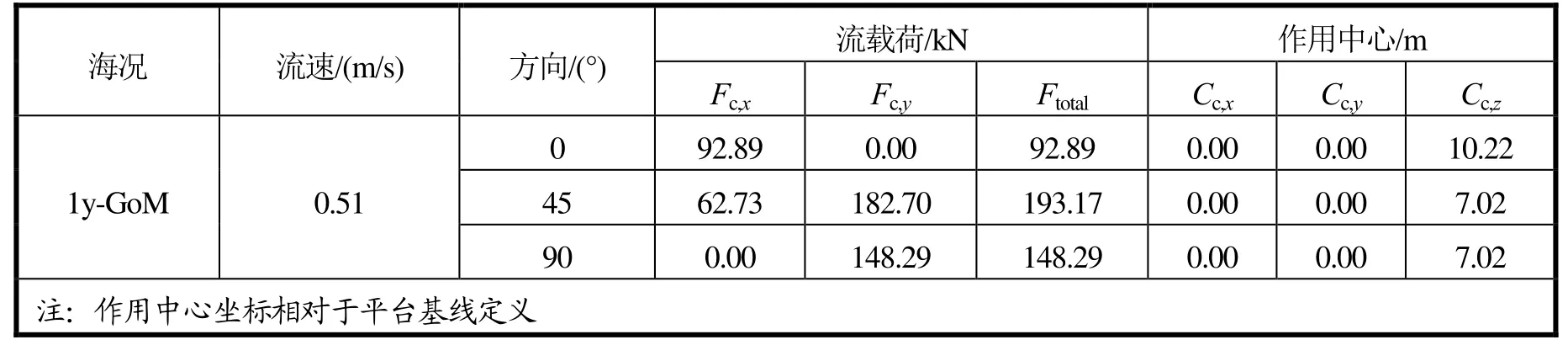

表3 标准型流载荷大小及作用中心

1.2.3 风荷载

标准型半潜生活平台的试验流速

V

及模拟海况见表4。标准型半潜生活平台受到的风载荷(

F

,

F

)及作用中心(

C

,

C

,

C

)通过风洞试验数据计算得到（见表5）。

表4 试验风速（全尺度）

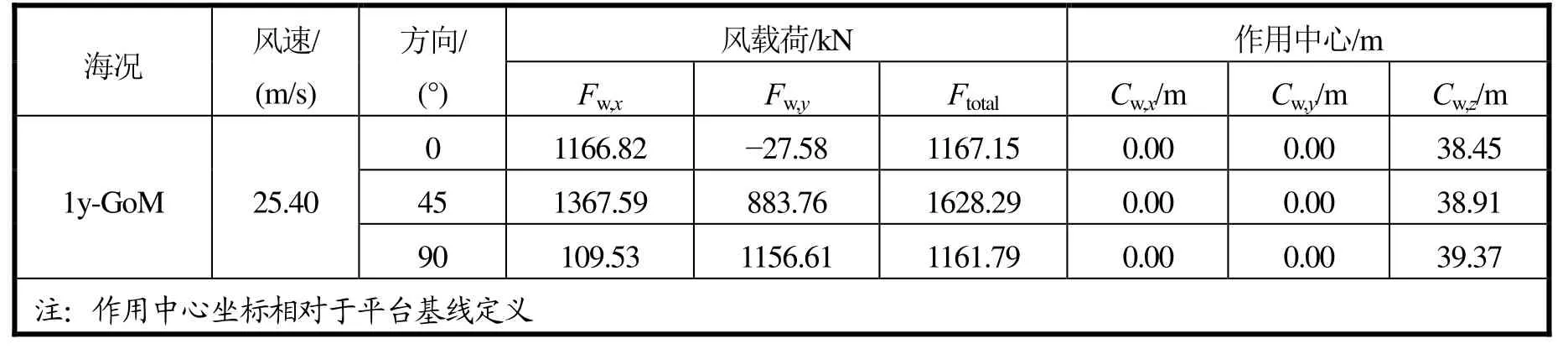
表5 标准型风载荷大小及作用中心

1.2.4 波浪

根据指定的有义波高、峰谱周期和波谱，对不规则波进行模拟。试验使用JONSWAP波浪谱，谱密度函数为

式中：

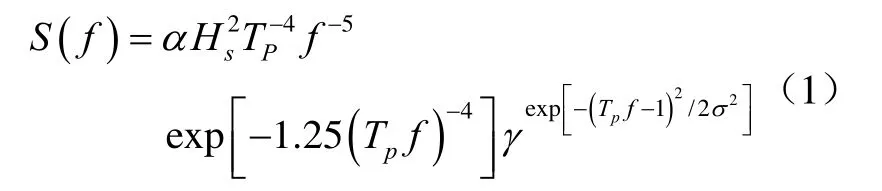
S

为波浪谱的谱密度函数；

α

为无因次常数；

H

为有义波高；

γ

为谱峰因子；

f

为波浪频率；

T

为谱峰周期；

σ

为谱峰形状参数。每一个不规则波的持续时间为3 h，保证纵荡、横荡和艏摇方向上的低频运动有足够的循环次数，实测有义波高

H

和峰谱周期

T

的误差应不超过理论值的3%，峰值谱密度误差应不超过5%，除波浪谱的尾部高频区域外，其它频率的谱密度误差应在理论值的20%以内。波浪条件见表6。

表6 波浪条件

2 非对称锚泊系统设计

本文采用以水动力性能分析为基础，建立的半潜式平台系泊系统模型，并采用势流理论分析计算波浪载荷，运用ECAT和NLID卡片模拟锚链的动态运动。通过研究平台的相对位移来分析不同非对称锚泊系统的特征。标准型半潜生活平台采用张紧式系泊系统，将API-RP-2SM规范作为参考依据，系泊系统由8根系缆组成，为4×2布置形式，定位锚索的编号从1～8进行变化。其中，1号和4号锚泊线与

x

轴的夹角为35°，5号和8号锚泊线与

x

轴的夹角为42.5°，相邻2根锚泊线之间的夹角为5°（见图 2）。每根缆绳为钢丝绳-锚链两段式，系泊初始参数见表7，缆绳材料参数见表8，不同位置处系泊缆的长度见表 9，缆绳导缆孔及锚点坐标见表10，其中导缆孔坐标和锚点坐标相对于标准型支持平台局部坐标系建立。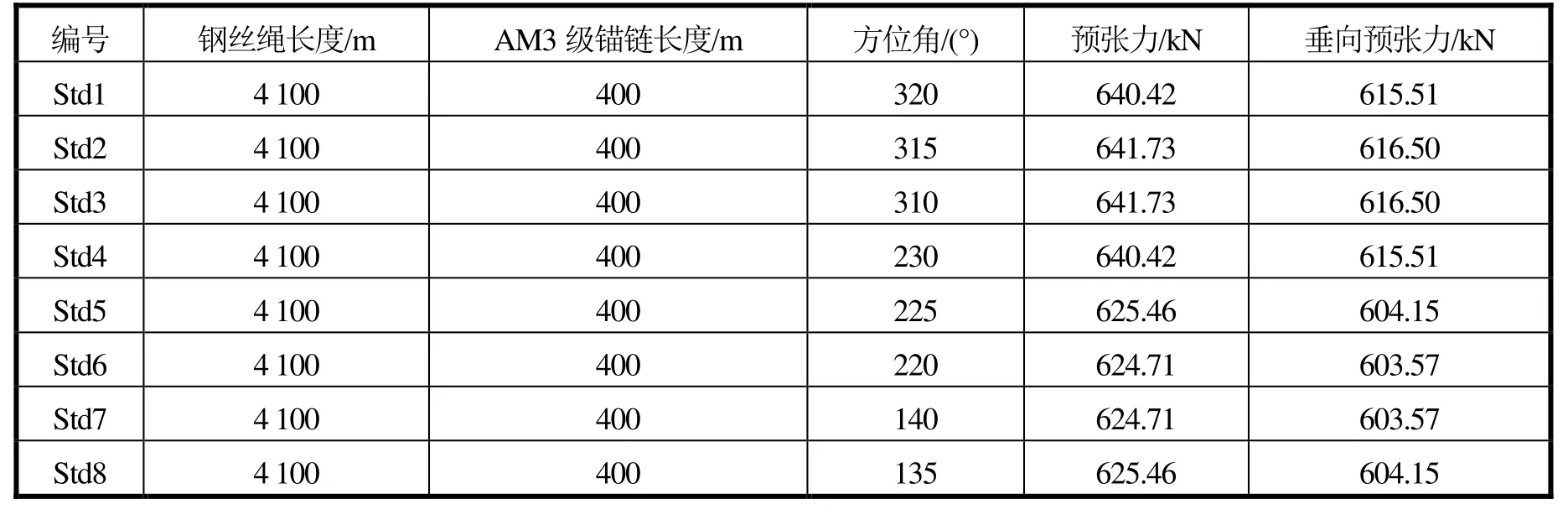

表7 标准型支持平台系泊缆初始参数（全水深）

表8 标准型支持平台系泊缆材料参数（全水深）

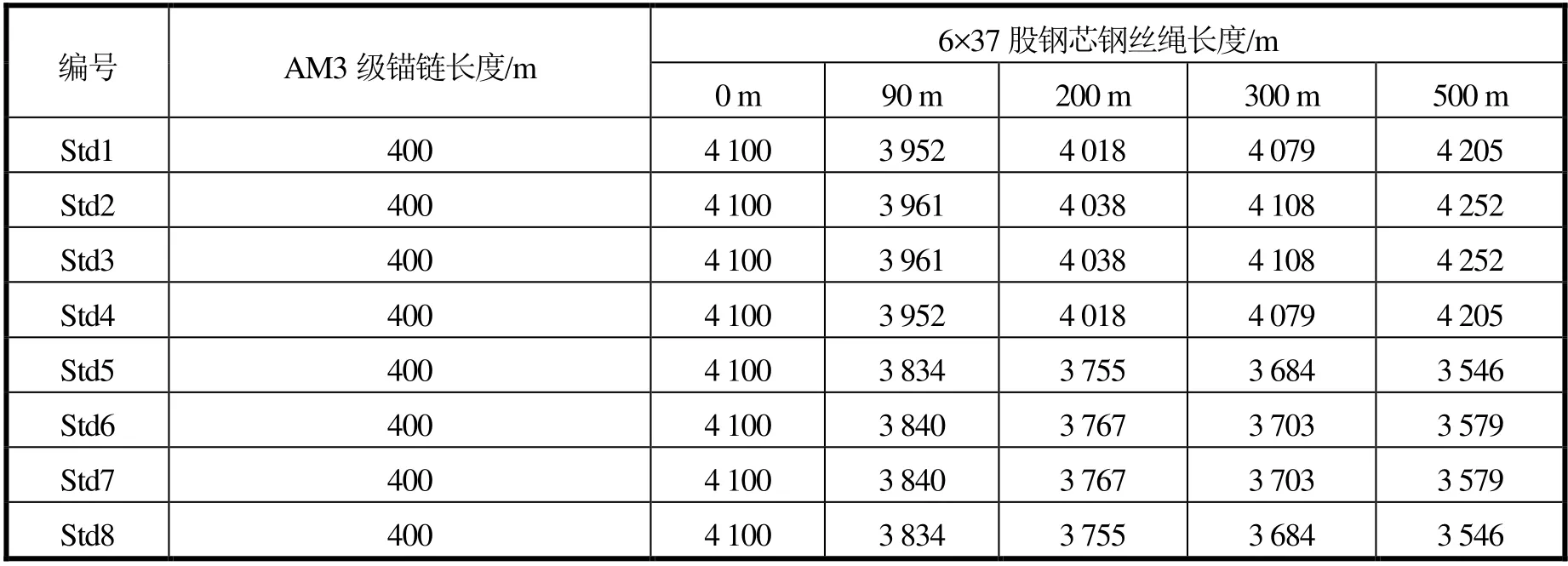
表9 标准型支持平台系泊缆不同位置下的长度（全水深）

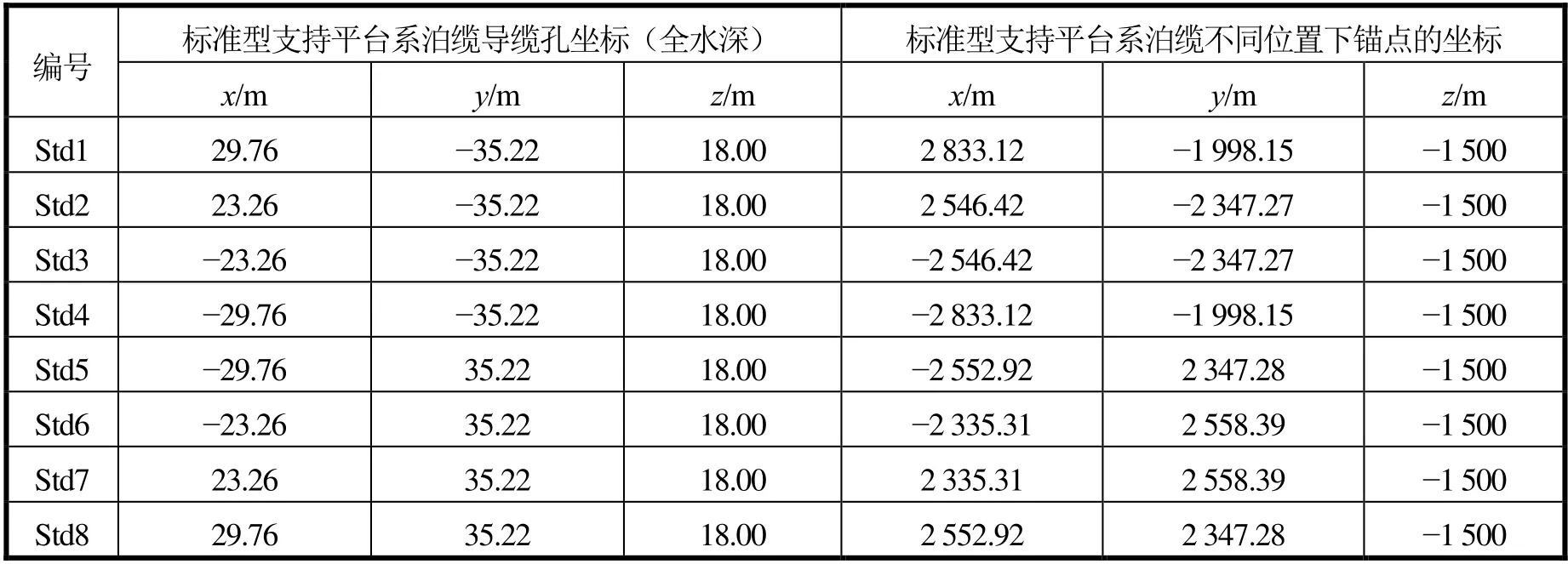
表10 导缆孔坐标和锚点坐标

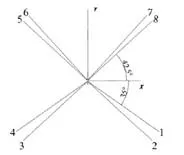
图2 标准型支持平台非对称系泊系统

3 标准型半潜生活平台锚泊系统数值计算

3.1 锚泊系统整体工况

标准型平台中心初始位置位于原点，平台沿着

y

轴正方向逐渐移动，改变平台的位置，而其他条件不变，研究平台非对称系泊方式的特点。。

在非对称系泊系统状态下，对平台锚链张力和平台响应进行研究。位置变化取3种不同变化量，分别计算平台各运动情况（见表11）。

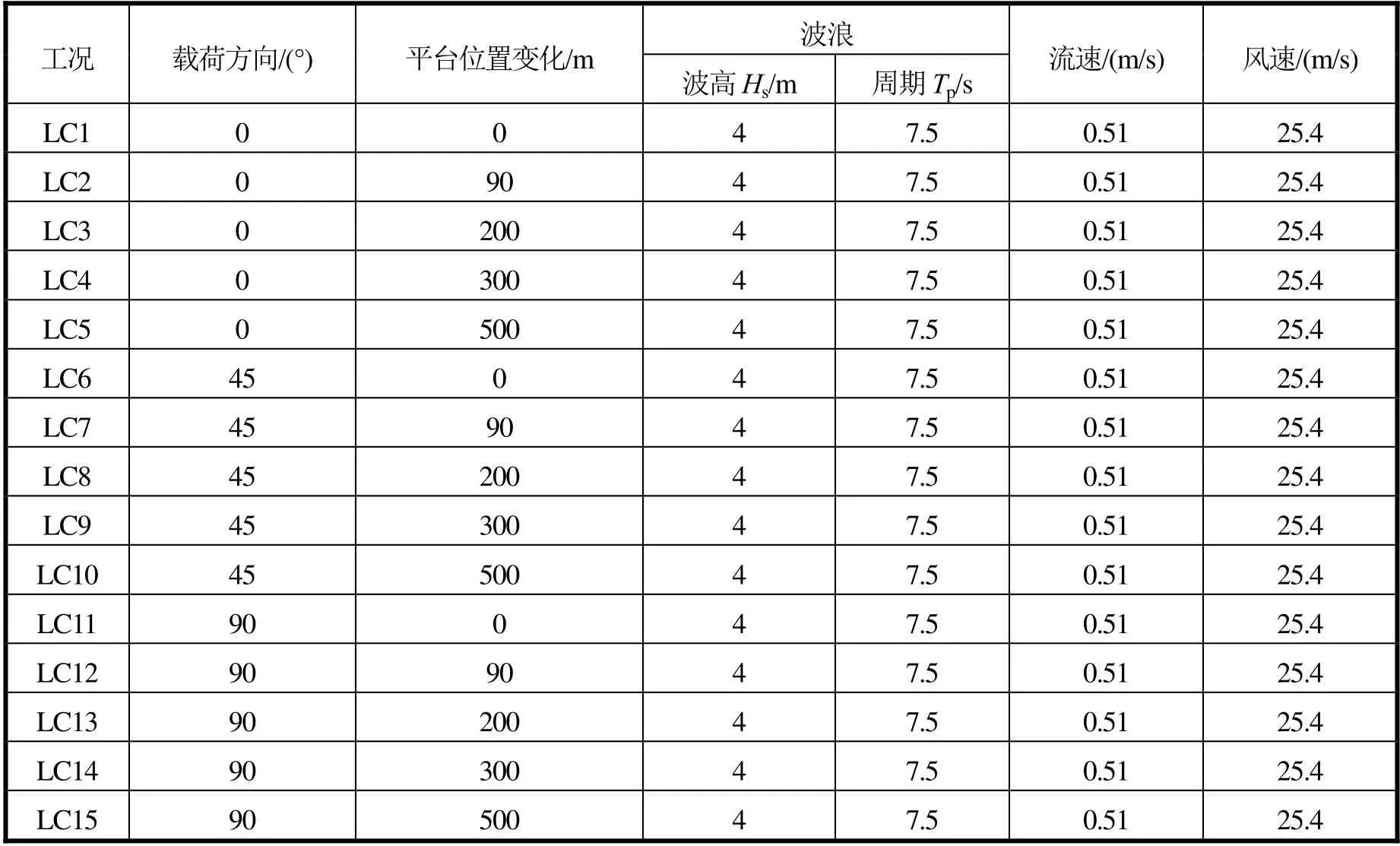
表11 深水半潜式支持平台工况表

3.2 锚泊系统计算

3.2.1 锚链张力分析与计算

在0°浪向上，锚链3～锚链6主要受力；在45°浪向上，锚链3～锚链6为主要受力；在90°浪向上，锚链1～锚链4为主要受力。

1）对于 0°浪向下的较短锚链部分，锚链最大张力出现在位置移动500 m时的锚链5上，最大张力为4.21×10N，安全系数为1.53，满足设计要求；如表12所示，锚链逐渐增长的部分最大锚链拉力逐渐减少，最大值为4.16×10N。

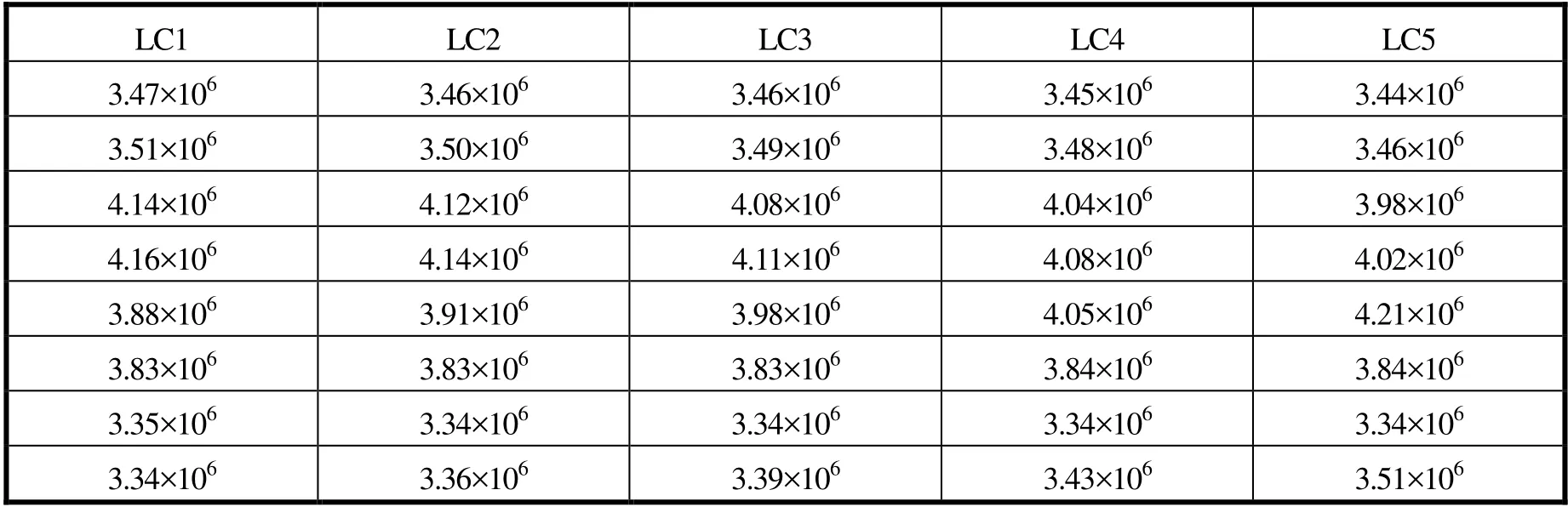
表12 0°浪向不同平台位置下标准型平台锚链最大张力（单位：N）

0°浪向下锚链最大张力随平台移动距离变化的情况如图3所示，在移动距离为300 m时达到最小值。

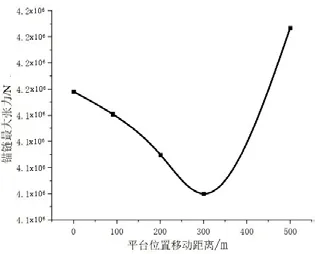
图3 0°浪向最大锚链张力随平台移动距离变化情况

2）45°浪向下，对于较长锚链部分，锚链最大张力出现在位置移动0 m的锚链4上，最大张力为4.32×10N，安全系数为1.48，满足设计要求；锚链较短部分的锚链最大张力逐渐增加，最大值发生在5号锚链上，最大值为4.09×10N，具体见表13。45°浪向下锚链最大张力随平台移动距离变化的情况如图4所示，锚链最大张力随平台移动距离的增大逐渐变小。

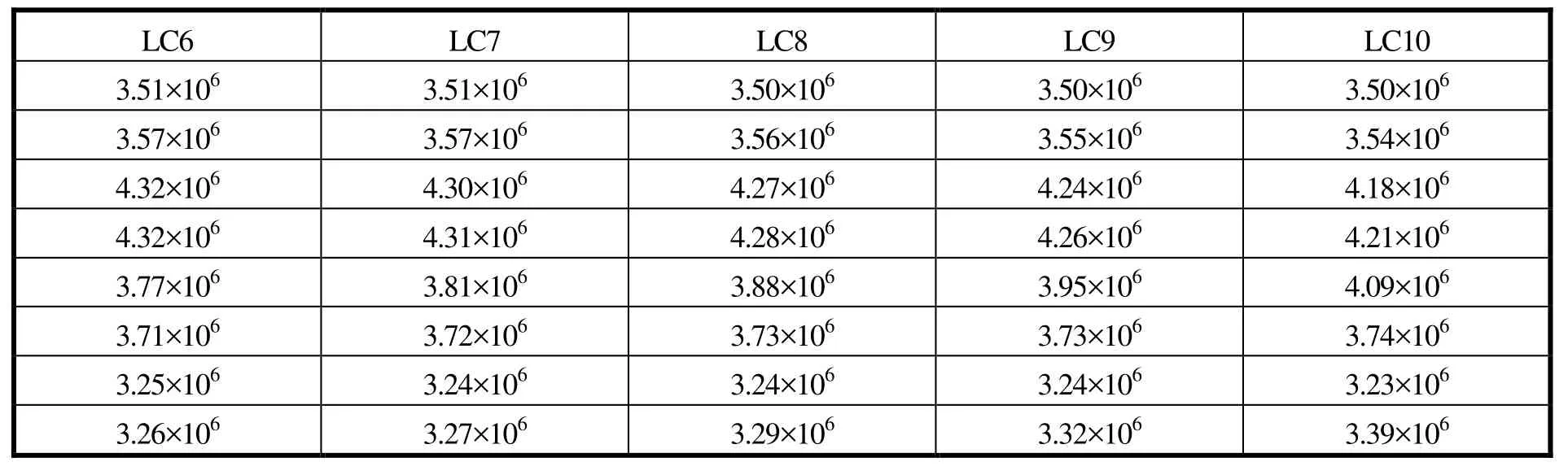
表13 45°浪向不同平台位置下标准型平台锚链最大张力（单位：N）

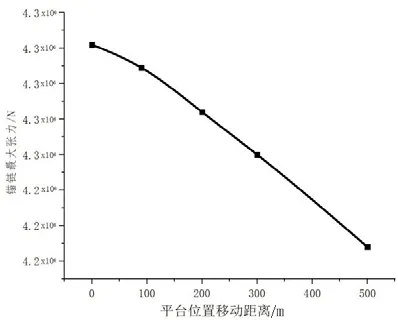
图4 45°浪向最大锚链张力随平台移动距离变化情况

3）90°浪向下，对于较长锚链部分，锚链最大张力出现在位置改变90 m的锚链3上，最大张力为3.86×10N，安全系数为1.67，满足设计要求；而对于较短锚链部分，最大值出现在锚链5上，锚链张力逐渐增加，最大值为3.80×10N，见表14。

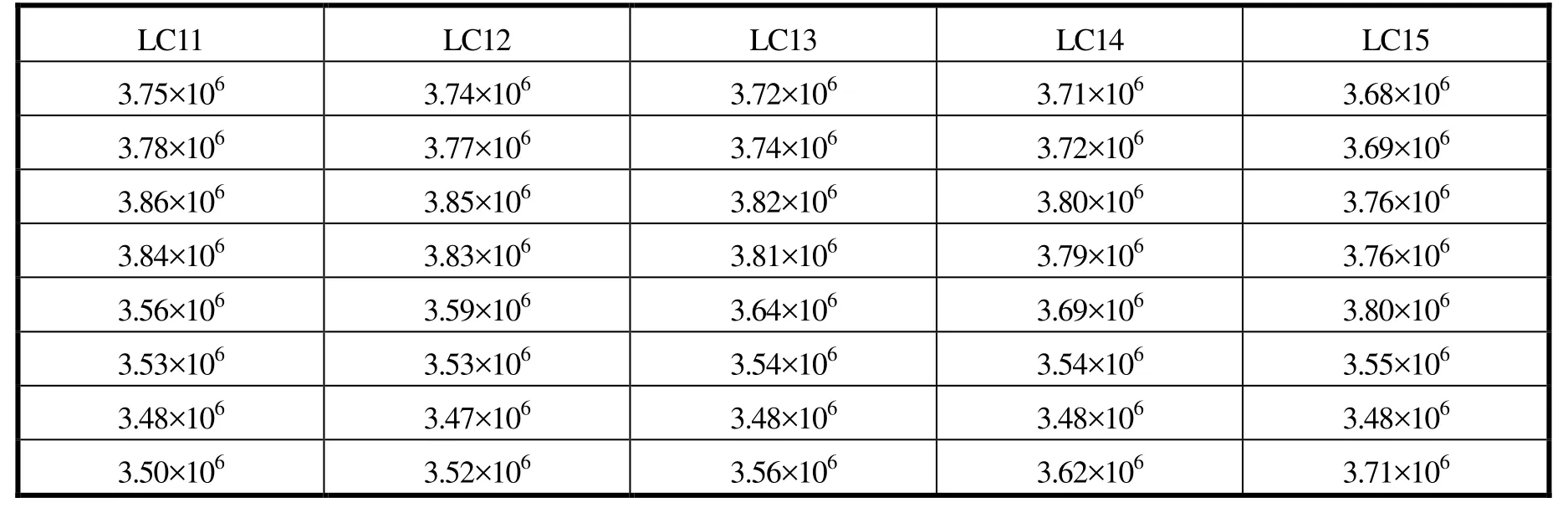
表14 90°浪向不同平台间隔下标准型平台锚链最大张力（单位：N）

90°浪向下锚链最大张力随平台移动距离变化的情况如图5所示，锚链最大张力在平台移动距离为400 m时达到最小值。

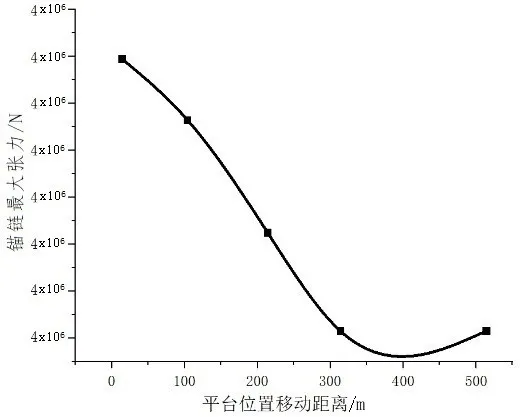
图5 90°浪向下不同平台位置最大锚链张力变化图

3.2.2 6自由度运动响应

1）0°浪向

横荡（Sway）的最大值出现在LC1，最大值为73.54 m，最小值为72.94 m。横摇（Roll）的最大值出现在LC1，最大值为1.112 m，最小值为1.044 m，而其余的自由度变化较小，具体见表15。0°浪向下横荡（Sway）和横摇（Roll）最大值呈不断下降的趋势，具体见图6。

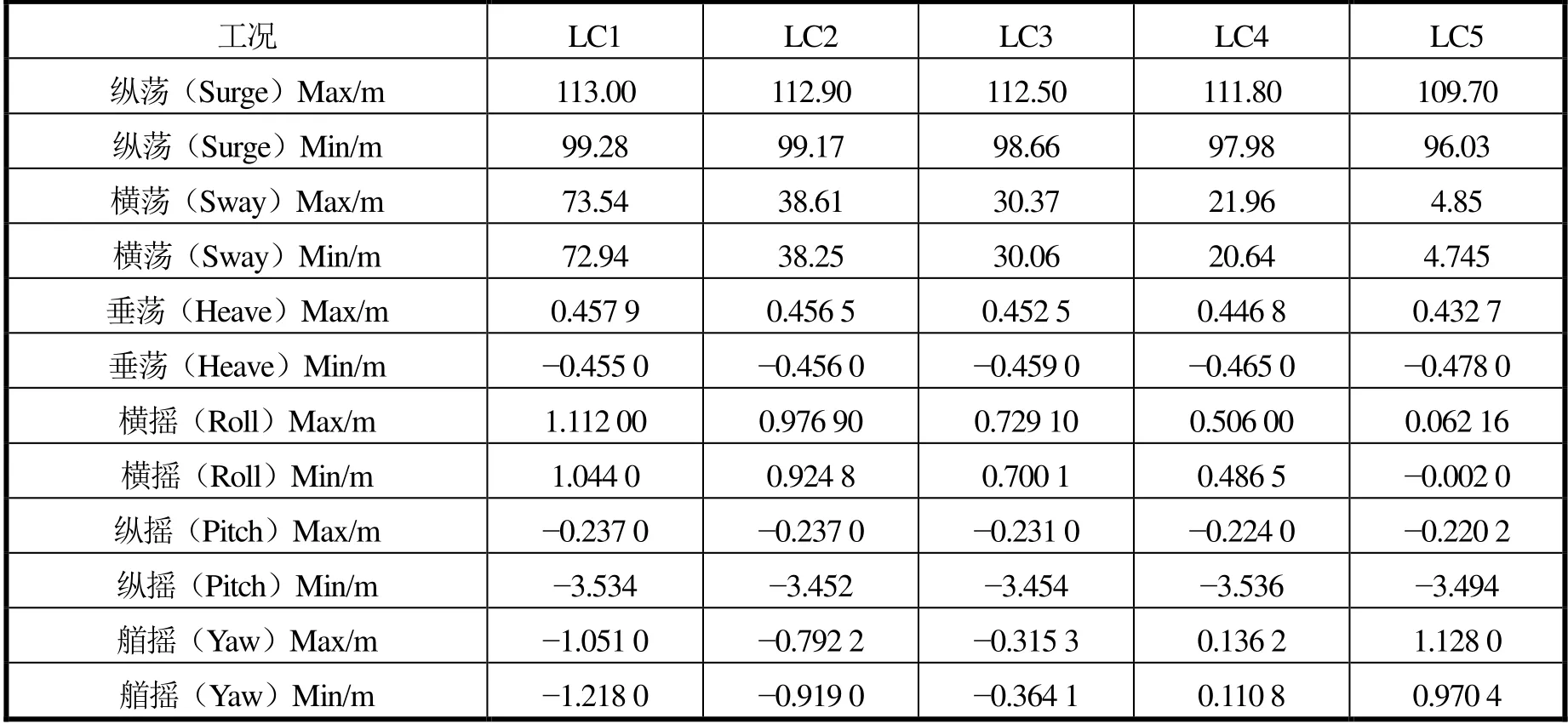
表15 标准型平台6自由度响应

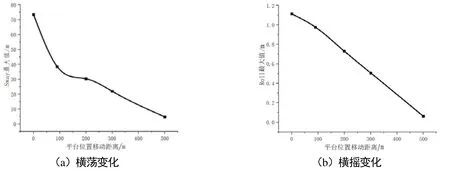
图6 0°浪向下不同平台位置横荡和横摇最大值变化图

2）45°浪向

横荡（Sway）的最大值出现在LC6，最大值为117.8 m，最小值为100.4 m。横摇（Roll）的最大值出现在LC6，最大值为3.107 m，最小值为0.756 7 m，而其余的自由度变化较小，具体见表16。

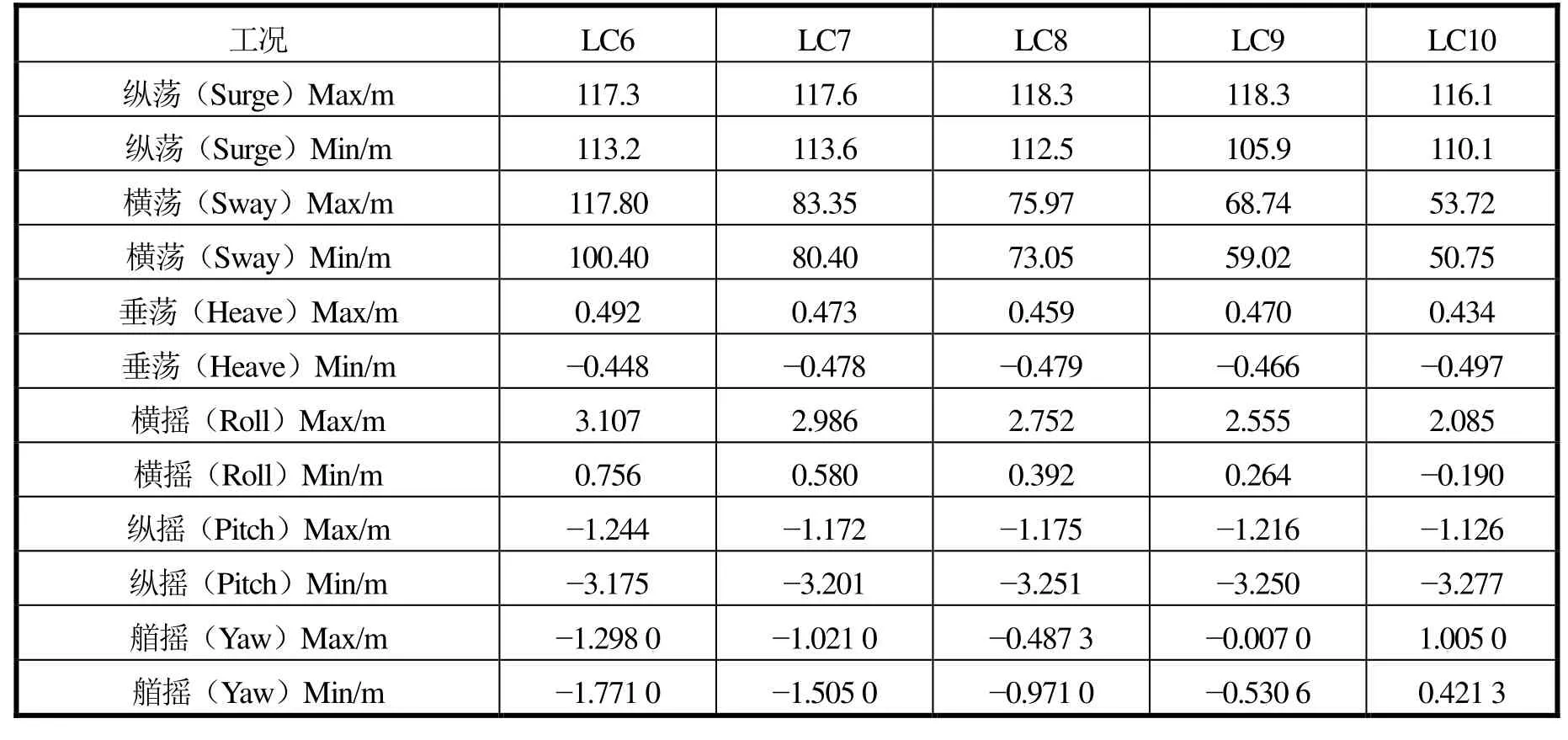
表16 标准型平台6自由度响应

45°浪向下横荡（Sway）和横摇（Roll）最大值呈不断下降的趋势，具体见图7。

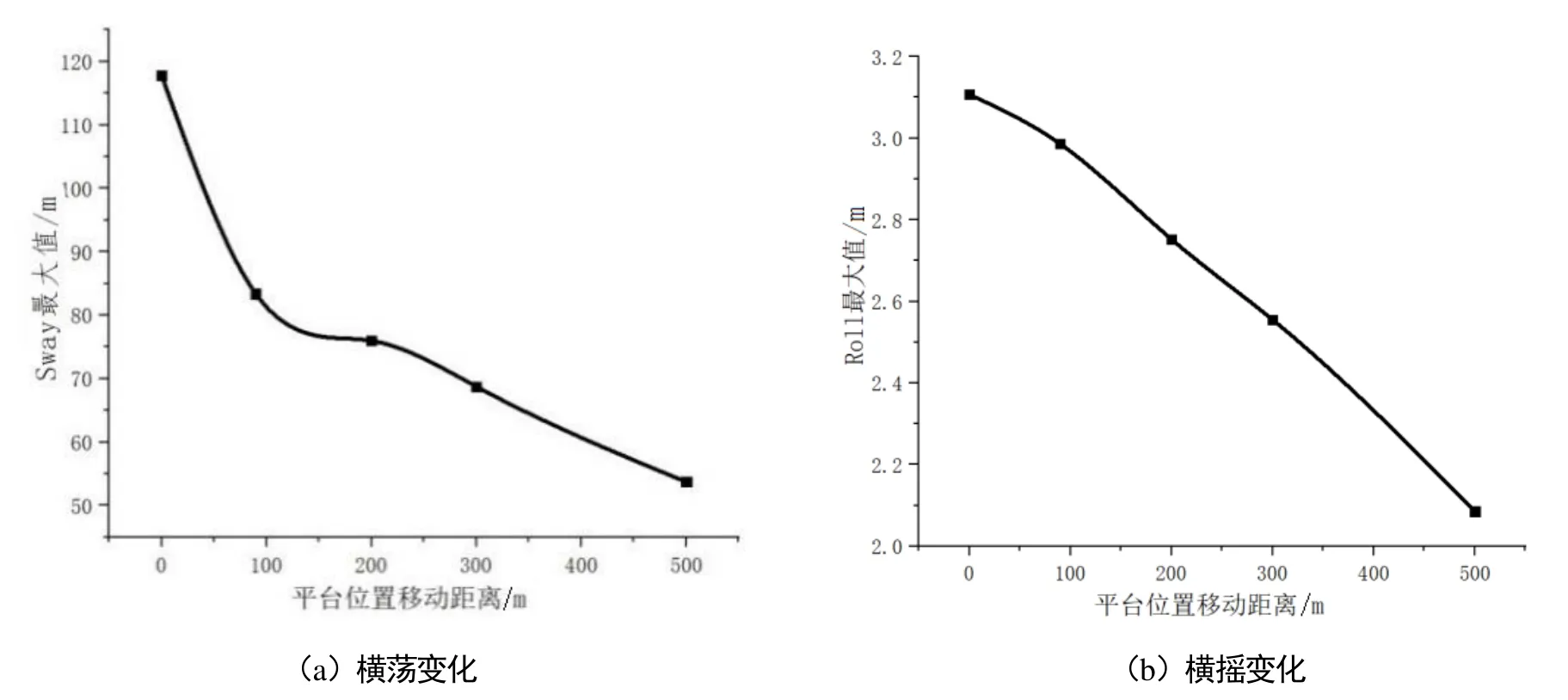
图7 45°浪向不同平台位置横荡和横摇最大值变化图

3）90°浪向

横荡（Sway）的最大值出现在 LC11，最大值为95.82 m，最小值为86.77 m。横摇（Roll）的最大值出现在 LC12，最大值为 3.464 m，最小值为1.107 m，而其余的自由度变化较小，具体见表18。

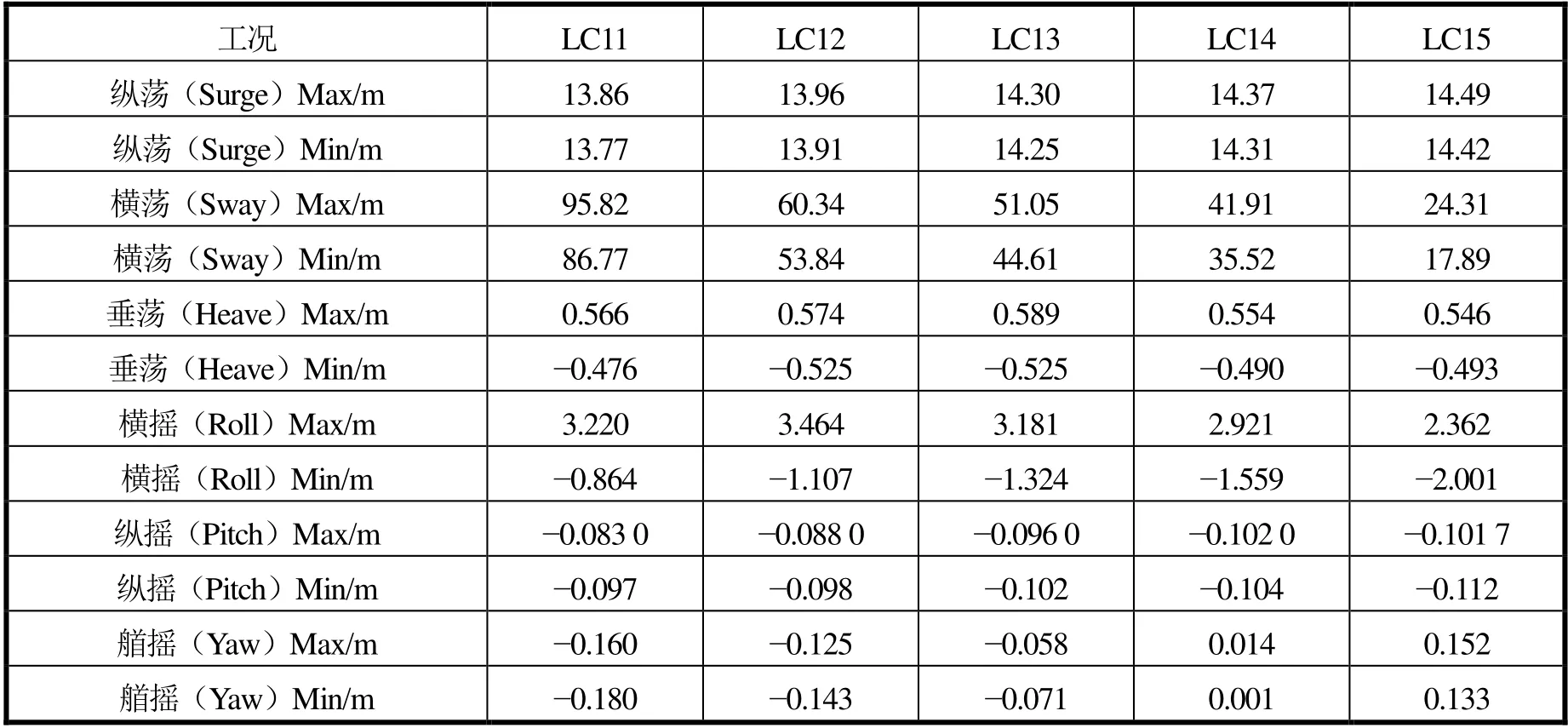
表18 标准型平台6自由度响应

90°浪向下横荡最大值呈不断下降的趋势，横摇最大值在平台位置移动90 m以下时呈增大的趋势，90 m处有最大值，在90 m以上处于不断减小趋势，具体见图8。

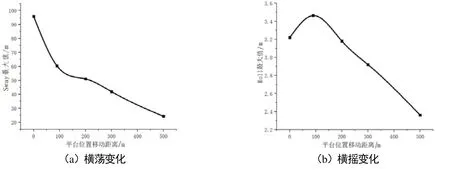
图8 90°浪向不同平台位置横荡和横摇最大值变化图

4 结论

通过对标准型半潜生活平台非对称锚泊系统进行时域分析，得出标准型平台在不同非对称系泊状态下，各个工况的锚链最大张力均能够满足设计要求的结论；锚链最大张力为4.32×10N。经过上述分析可以发现，随着锚链布置的非对称性突出，锚链的张力变化较为明显，特别是锚链的较短部分，锚链张力明显增加，而随着锚链增长锚链的最大张力增加，由于工作环境条件较柔和，锚链张力变化幅度不是太明显，变化量约为10%。此外，在不同的非对称形锚泊系统工况中，平台的运动变化非常明显，变化量可达60%～80%，由此可见，非对称系泊对平台的运动性能影响非常显著。希望本研究结果能对标准型半潜生活平台非对称系泊系统的设计有一定的指导意义。