高倍率工况下锂离子电池的建模

高 原,黄荣杰,秦东晨,王婷婷

(1.郑州大学机械与动力工程学院,河南 郑州 450001;2.郑州轻工业大学机电工程学院,河南 郑州 450001)

电池剩余电量、寿命、温度等状态的准确估算是保证电动汽车安全、高效运行的前提[1],并且都依赖于准确的电池模型。等效电路模型能很好地反映锂离子电池的外部特性,被人们广泛采用。等效电路模型的内部参数通常可以认为是关于温度[2]和荷电状态(SOC)[3]的函数,但是没有考虑电流引起的参数变化。电动汽车的行驶工况复杂多变,在高速行驶、爬坡等阶段,锂离子电池的放电电流通常会达到3C,而在一些特种电动车辆中,峰值放电电流甚至可达到10C。一方面,电池容量、电阻等参数在高倍率放电时会发生改变;另一方面,电流的增大会导致电池温度明显上升,影响电池模型的精度。

基于以上分析,本文作者提出一种综合考虑电流和温度影响的锂离子电池电热耦合模型,以追踪高倍率电流工况下电池参数的变化和温度的改变;通过混合功率脉冲特性(HPPC)实验,获取不同倍率电流工况、温度以及SOC区间的阻抗参数;最后,对电热耦合模型在高倍率电流工况和不同温度下的动态工况进行验证。

1 电池模型

1.1 考虑电流和温度影响的锂离子电池电模型

对传统等效电路模型进行改进,将电池参数设置为电流、温度和SOC相关的变量,以模拟锂离子电池在不同负载电流、电池温度和放电区间下参数的变化。改进后的模型如图1所示。

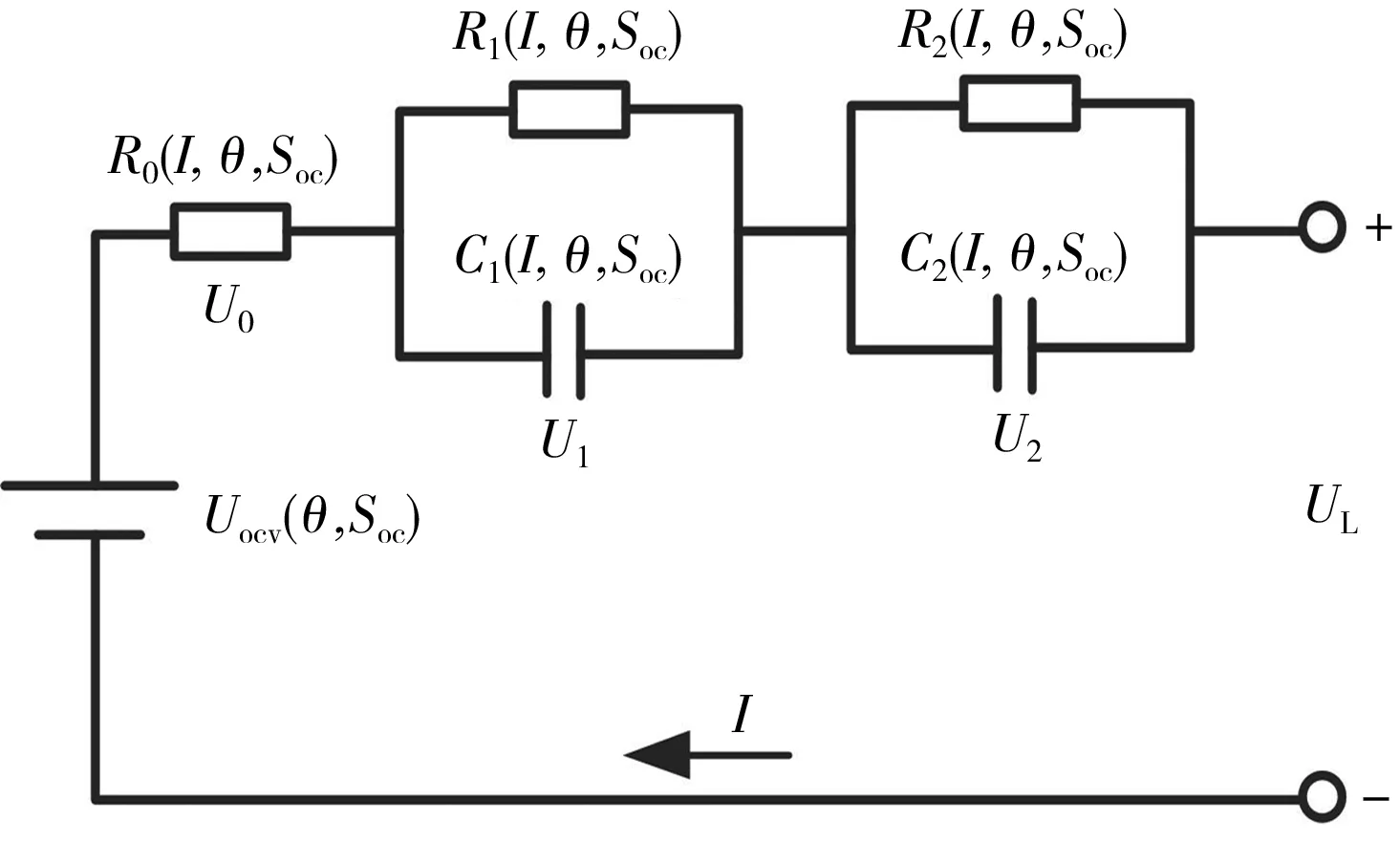
图1 考虑电流和温度影响的等效电路模型Fig.1 Equivalent circuitmodel considering the effect of current and temperature

图1中:R0为欧姆内阻;R1、C1分别为电化学极化电阻和电容;R2、C2分别为浓度差极化电阻和电容;I为负载电流;θ为温度;Uocv为开路电压;Soc为电池的SOC;U0为欧姆内阻的端电压;U1、U2分别为两个RC网络的端电压;UL为电池的端电压。R0、R1、C1、R2和C2均为关于电流、温度和SOC的变量。

根据基尔霍夫定律,改进后等效电路的数学模型可以表示为:

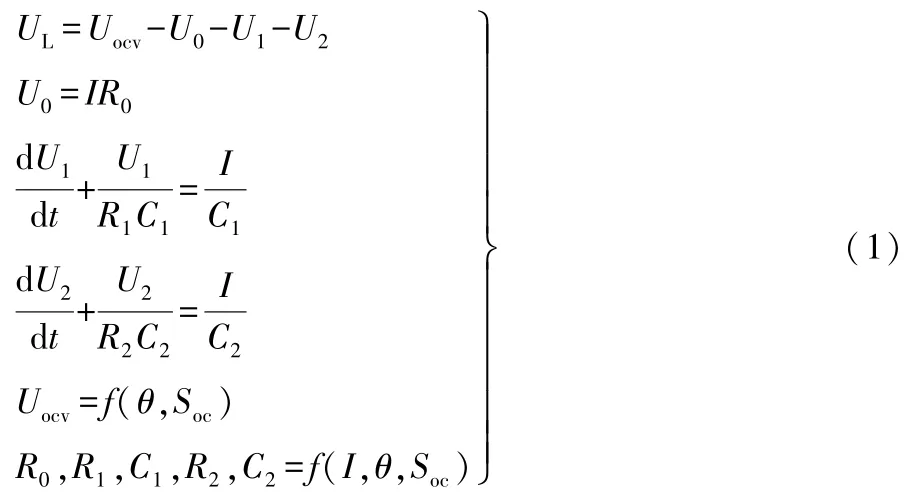
1.2 锂离子电池热模型

锂离子电池热量来自于自身内部产生的化学热和与外界的交换热。假设锂离子电池外表面各处的温度是一致的,电池与外界环境的热交换也是稳定的,结合热力学第一定律,锂离子电池热模型可以表示为:

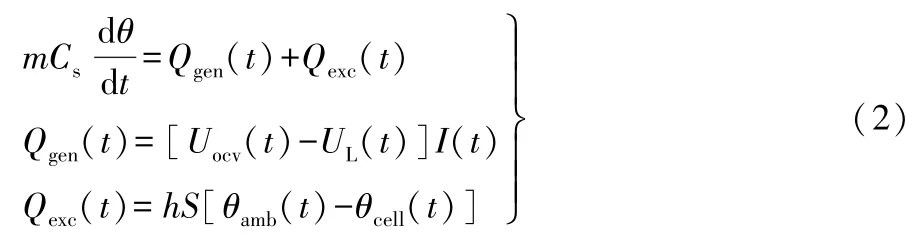
式(2)中:Qgen为电池产生的化学热;Qexc为电池的交换热;m为电池质量;Cs为电池的比热容;h为电池的热交换系数;S为电池的表面积;θamb为环境温度;θcell为电池的表面温度;t为时刻。

1.3 锂离子电池电热耦合模型

电模型输出的电池参数是热模型的输入量,同时,热模型输出的电池温度也是电模型的输入量,两者相互耦合,最终输出电池的端电压。

根据式(1)、(2)建立的锂离子电池电热耦合框架如图2所示。

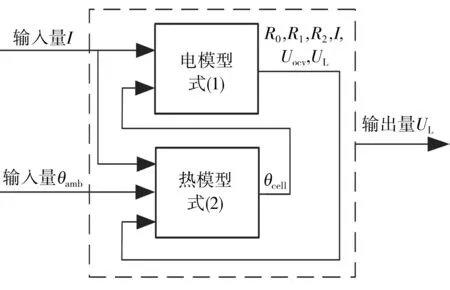
图2 电热耦合框架图Fig.2 Frame diagram of the electro-thermal coupling

该模型需要识别的参数有:阻抗参数R0、R1、C1、R2和C2,以及热交换系数h等。

2 高倍率电流工况下电池参数识别

2.1 电池实验平台

实验对象为电动汽车用20 Ah磷酸铁锂正极锂离子电池(广东产),主要参数为:标称电压3.2 V,工作电压2.50～3.65 V,比热容1.06 J/(g·K)。

电池测试平台所用仪器包括:控制充放电和监控电池状态的CT-6001A电池测试系统(武汉产),控制电池环境温度的BLC-300温控箱(上海产),监控电池表面温度的UTi-380H热成像仪(东莞产),以及用于数据处理的主机。

2.2 阻抗参数识别和分析

分别在5℃、15℃、25℃、35℃和45℃下,在100%～0 SOC范围内,每隔10% SOC,分别以0.5C、1.0C、2.0C和3.0C的电流在2.50～3.65 V进行HPPC测试[4],识别电池阻抗参数。

锂离子电池的欧姆内阻R0可以根据放电脉冲开始和结束时的电压下降量来计算,极化参数R1、C1、R2和C2可以通过拟合HPPC实验中的电压曲线获得,具体的计算步骤参见文献[5]。

最终识别出的阻抗参数与电流倍率、温度和SOC的关系如图3和图4所示。

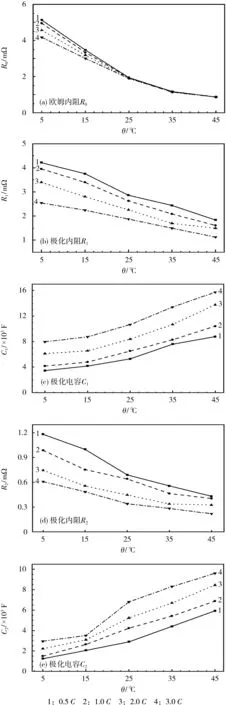
图3 不同电流倍率下锂离子电池阻抗参数与温度的关系Fig.3 Relation between the impedance parameters and temperatures of battery at different current rates

图4 不同温度下锂离子电池阻抗参数与SOC的关系Fig.4 Relation between the impedance parameters and state of charge(SOC)of battery at different temperatures

从图3、4可知,R0、R1和R2受电流影响的趋势相同,均随着放电电流的增大而减小。巴特勒-福尔默方程表明,电池的电荷转移内阻随着放电电流的增大而减小,同时,电流较小时,Li+的能量较低,跃过界面壁垒能力较差,因此,极化电阻更大。欧姆内阻R0及极化内阻R1、R2都随着温度的下降而升高,原因是低温环境下,活性物质的扩散能力、电解液的导电率都会急剧下降,造成电阻下降。

2.3 热特性参数识别

热模型中的热交换系数h可通过电池高倍率电流放电,温度急剧升高后,静置阶段的冷却温度曲线获得[6]。实验记录的电池中心温度为38.5℃,最高温度点为39.1℃,两者仅相差0.6℃。为方便计算,假设电池表面各处温度一致,在无负载电流状态下,电池的密度、比热容和热交换系数h及所处的环境温度是恒定的。

静置阶段电池的发热量Qgen(t)=0,求解式(2),可得到表面温度随时间变化的方程。

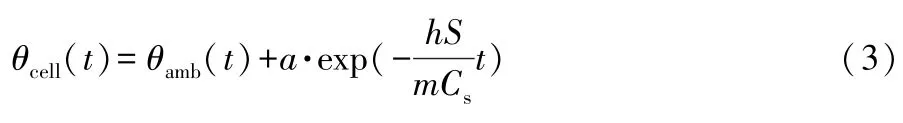
式(3)中:a为拟合系数;exp是以自然常数e为底的指数函数。

根据在25℃环境下进行的电池冷却实验及式(3),拟合得到的热交换系数h=16.04W/(m2·℃ )。

3 模型验证与分析

根据电热耦合模型和识别的参数,在MATLAB/Simulink环境下搭建锂离子电池仿真模型。

为验证电热耦合模型的准确性,分别对模型在不同倍率恒流放电工况和不同温度下进行4个连续的新欧洲行驶循环(NEDC)工况(电流曲线见图5)仿真,并将得到的端电压、电池温度与实验数据进行对比。

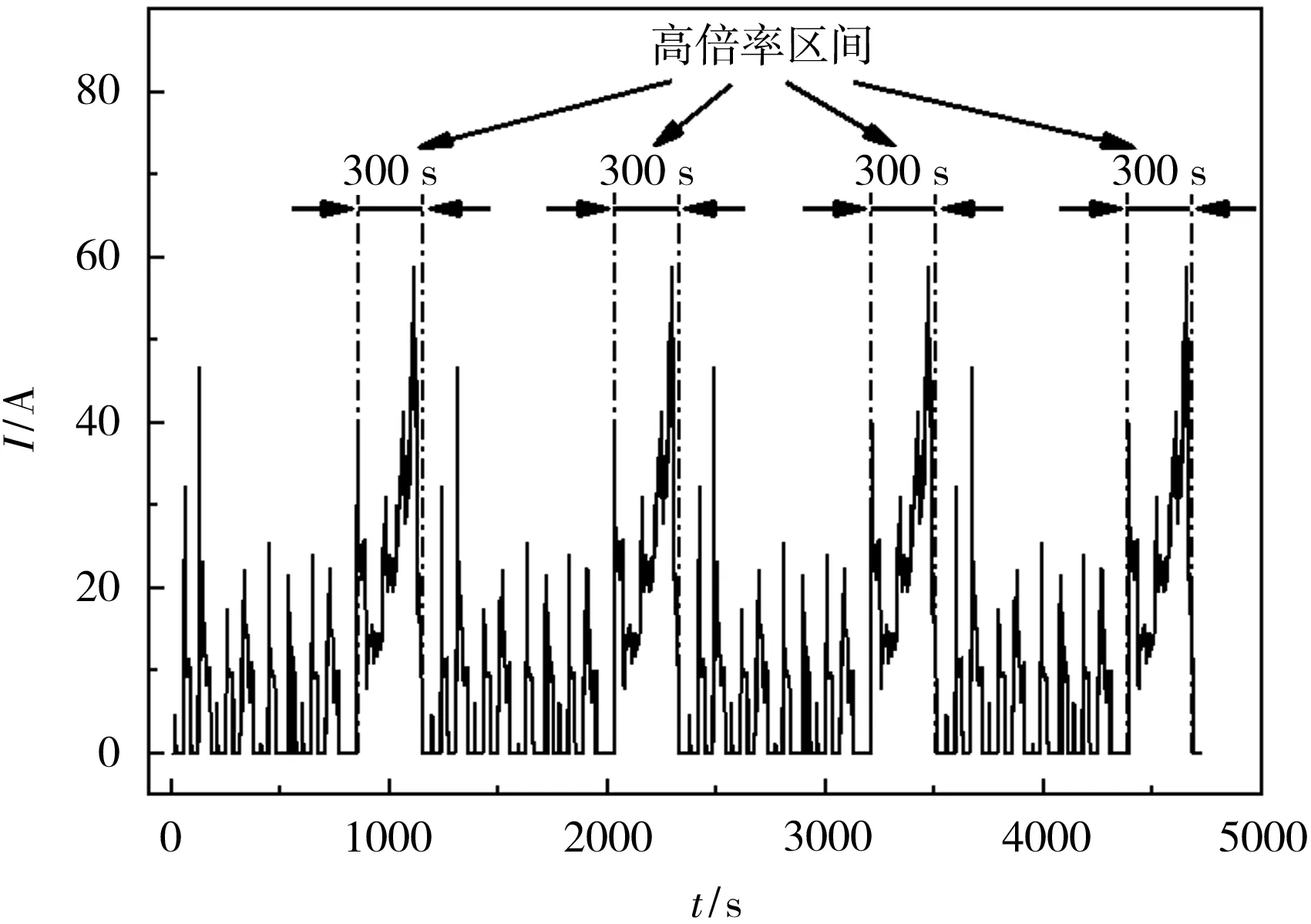
图5 NEDC工况的电流曲线Fig.5 Current curve of new European driving cycle(NEDC)condition

搭建不考虑电流影响的电池模型作为对比。该电池模型的参数是在与电热耦合模型相同的条件下,以0.5C倍率实验得到的。

采用如式(4)所示的均方根误差(RMSE,ERMSE)和平均绝对误差(MAE,EMAE)来评价模型的准确性。

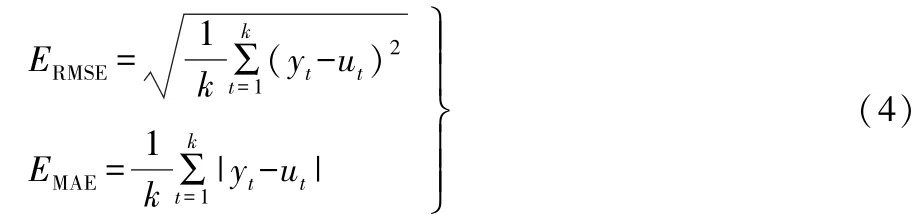
式(4)中:y t为仿真值;u t为实验数据;k为样点个数。

3.1 高倍率恒流放电工况验证

锂离子电池在高倍率恒流放电工况下仿真和实验所得温度和端电压数据如图6所示。

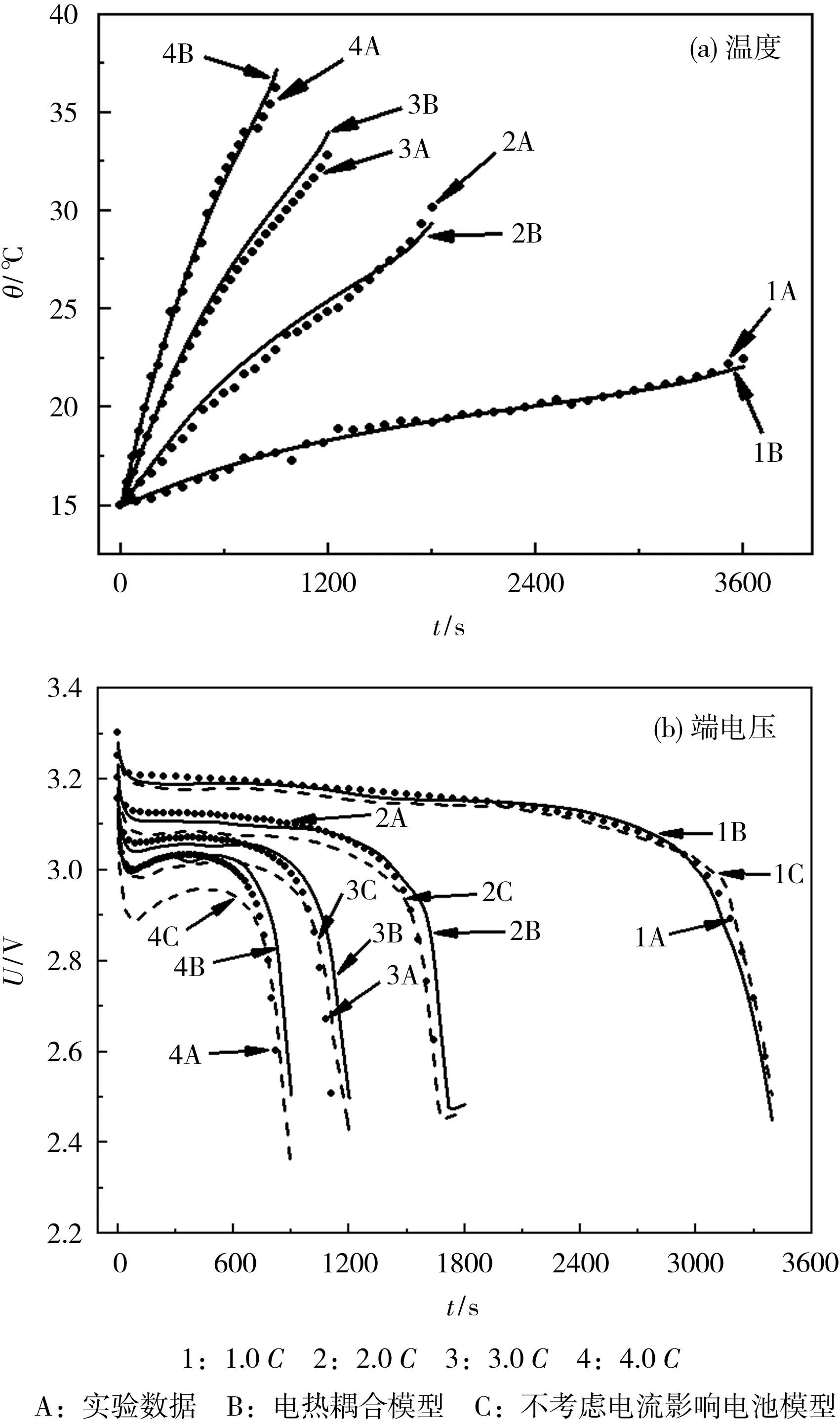
图6 15℃下高倍率恒流放电工况验证结果Fig.6 Verification results under high rate constant current discharge conditions at 15℃

从图6可知,电热耦合模型在1.0～4.0C电流倍率下的仿真结果均与实验数据吻合良好。在1.0C电流倍率下,是否考虑电流影响的端电压相差不多,但当电流加大时,两者发生明显偏离。电池内阻随着放电倍率的增大而减小,因此在2.0～4.0C电流倍率下,不考虑电流影响的对比模型(参数识别电流为0.5C)所得的仿真电压,低于实验数据和电热耦合模型仿真电压。以3.0C、4.0C倍率放电时,实验和仿真的电池端电压都出现了反弹,而不是随着放电时间延长而持续减小。这是由于电池在高倍率放电工况下,温度明显升高,如图6(a)所示,在3.0C和4.0C倍率下,电池的温升分别为17.8℃和21.2℃。电池温度升高,内阻显著降低,因此端电压会升高反弹。

3.2 NEDC工况验证

在15℃下,NEDC工况仿真得到的电池端电压、实验数据及误差如图7所示。

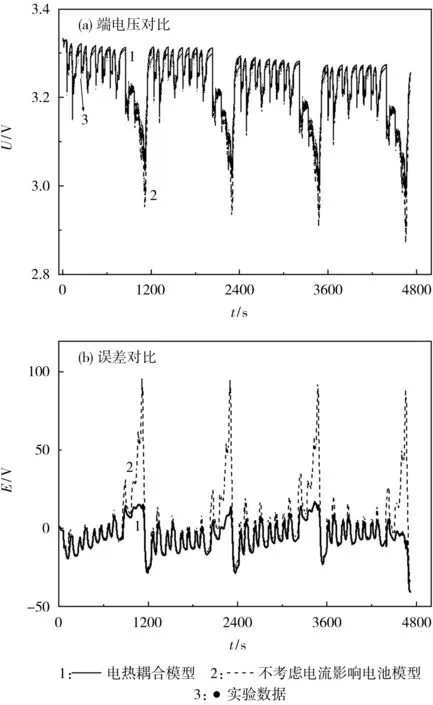
图7 15℃下NEDC工况验证结果Fig.7 Verification results under NEDC condition at 15℃

从图7可知,电热耦合模型仿真结果与实验数据高度吻合,模型表现整体稳定,没有随温度和电流的改变而出现较大的误差。仿真结果的最大误差为17.1 mV,相比不考虑电流影响的电池模型减少了82.2%。两种模型与实验数据的走势基本相同,所得端电压都随着时间和放电电流的增大而减小,但不同区间两种模型的误差略有不同。在NEDC工况的低倍率电流区间,电池负载电流较小,电流的小范围波动不会引起电池参数的明显变化,因此两种模型的仿真结果均与实验数据接近。在NEDC工况的高倍率电流区间,电流的急剧增大引起电池容量的减小和电阻的降低,此时,电流倍率成为影响电池参数的重要因素,若忽略电流的影响,会增大仿真误差。

两种模型在5～45℃内NEDC工况下的RMSE和MAE见表1。

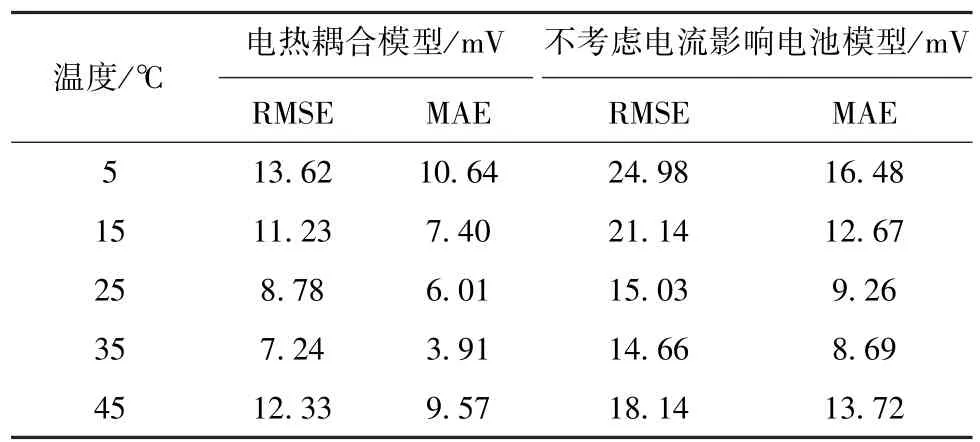
表1 不同模型的端电压误差Table 1 Terminal voltage errors of differentmodels

从表1可知,在所有的测试温度范围之内,电热耦合模型的精度均有明显改善。相比不考虑电流影响的电池模型,在5℃、15℃、25℃、35℃和45℃下,RMSE分别减少了45.5%、46.9%、41.6%、50.6%和 32.1%;MAE分别减少了35.4%、41.5%、35.1%、55.0%和30.2%。

综上所述,考虑电流影响的电热耦合模型,可以很好地模拟出宽温度和电流倍率范围内锂离子电池的电压响应。改进后的锂离子电池模型适用于电动汽车,尤其是高倍率电流运行场景。

4 结论

为提升高倍率工况下锂离子电池模型的精度,本文作者构建了一种考虑电流和温度影响的锂离子电池电热耦合模型,主要结论如下:

高倍率电流会引起锂离子电池内部参数的改变,造成电池温度的急剧上升;同时,温度也会影响锂离子电池的内部参数。在搭建电池模型时,应考虑两者的电热耦合关系。

验证结果表明,与现有模型相比,考虑电流影响的电热耦合模型可以大幅减小高倍率放电工况下的误差,在NEDC工况5℃、15℃、25℃、35℃和45℃下的MAE分别减小了35.4%、41.5%、35.1%、55.0%和30.2%,具有更好的模型精度和稳定性。