机器学习模型在滑坡易发性评价中的应用
刘福臻,王 灵,肖东升
(西南石油大学土木工程与测绘学院,四川 成都 610500)
0 引言
滑坡是我国西南地区最为常见的地质灾害,由于滑坡发育的复杂性和非线性,目前还没有一套完全成熟的理论能对其进行有效的防治。而我国西南片区受地形地貌、地质构造等复杂环境的影响,更是为滑坡的发育提供了有利条件。为加强对西南片区滑坡的防治和管理,对该区域进行精确的滑坡易发性评价具有重要的现实意义。
滑坡易发性评价主要研究内容是:在区域范围内,某一确定位置在确定条件下发生滑坡的空间概率[1]。作为判断滑坡危险性和风险性的基础,易发性评价是防灾减灾中不可缺少的工作[2]。国内外学者对滑坡的易发性评价开展了一定程度的研究,这些研究大多集中在易发性模型的选择以及量化方法上,而少有学者对其非滑坡样本的选择进行研究。对于回归性和预测性模型而言,样本的选择通常决定了整个模型的精确性和稳定性,若将一些高易发区的点位作为了非滑坡的样本,模型的适用性会大打折扣。为了更加精准的表达滑坡的易发性分区,有必要对样本的选择进行一定程度的研究。
一般认为,滑坡的易发性评价体系包含评价指标的量化和评价模型的选择这两个过程。常用的量化方法有专家打分法[3]、信息量法[4]、证据权法[5]、确定性系数法[6]和频率比法[7]等。在评价模型上,常用的模型有层次分析法[8]、模糊综合评判法[9]、灰色理论[10]、粗集理论[11]、分形理论[12]以及近年来发展迅速的机器学习法[13]。实验选择频率比法作为滑坡易发性的指标量化方法,该方法从数据本身的结构信息出发,打破了人为主观给分的限制,从而实现了滑坡因子二级属性的客观量化。评价模型上,由于机器学习能够更为准确的反应滑坡易发性与各评价因子之间的非线性关系[14],实验选择了机器学习中的聚类模型和回归模型,利用两个模型的有机结合,不仅解决了回归模型中训练样本的选择问题,同时实现了滑坡易发性指数与各评价因子之间的非线性回归。
1 研究区概况及数据源
1.1 研究区概况
南江县位于我国四川省巴中市西北部,是巴中连接汉中市的重要交通枢纽。全县幅员辽阔,总面积3 382.8 km2,是巴中市海拔最高的一个县,巴中市海拔高度大于1 800 m 的山体90%以上分布在南江县,且地形起伏大,最高地段海拔达2 493 m,而最低为332 m。复杂多变的地质、地貌条件为南江县带来了丰富的矿产资源,同时也为地质灾害的孕育提供了有利条件,其中地质灾害以滑坡为主。南江县在巴中市的地理位置及其1958—2009年的历史滑坡点位置如图1所示。

图1 研究区地理位置及历史滑坡点分布图Fig.1 Geographical location of the study area and historical landslide distribution map
1.2 数据源
实验用到的数据有南江县1958—2009年地质灾害详查汇总表、南江县DEM、南江县 1∶25 万地质图(表1)。通过DEM 提取出坡度、坡向、坡型、水系和高程的初始状态因子。将地质图矢量化后转为栅格数据,从而获取地层岩组因子。以上因子全部投影到同一坐标系下,并重采样为30 m×30 m 的栅格,全区共分为3 784 091 个栅格,其中滑坡占了359 个。

表1 数据源Table 1 Data source
2 模型介绍
2.1 频率比法
评价因子的量化一直以来都是评价模型中最为重要的一环,通常情况下因子的量化值都是采用专家经验打分,该方法虽然操作简单快捷,但存在的主观性太大。文章选择频率比法作为量化模型,该模型从统计学原理出发,将历史滑坡点数据和评价因子二级属性进行叠加分析,从而实现了评价因子的客观量化,见式(1)。

式中:Xi——因子X在二级属性i下的频率比值;
ni——因子X在二级属性i下的滑坡个数;
si——研究区内因子X在二级属性i下的栅格个数;
N——研究区总滑坡个数;
S——研究区总栅格数。
2.2 机器学习
机器学习的应用主要包含回归、分类、聚类和数据降维四大领域。各模块的相互结合更能突出机器学习的优势。本次实验将聚类思想和回归思想相结合,用于南江县的滑坡易发性评价。实验的算法和数据分析通过Python 编程平台实现,空间分析模型和出图模块由ArcGIS 平台完成。通过Python 和ArcGIS 的结合,可以方便且快速的对地理空间数据进行分析。
2.2.1 k 均值聚类
k 均值聚类算法能在没有先验数据的情况下,对原始数据进行初步分类,分类结果通过后续的信息补充加以验证。其思想是,随机选择k 个样本数据作为聚类中心,计算出每个样本与聚类中心的距离,并把相近的样本作为一类。每分配一个样本时,聚类中心会根据当前类中出现的样本重新计算,反复迭代这一过程,直到聚类中心不再发生变化为止[15]。
2.2.2 神经网络
神经网络算法通过模仿生物神经网络的结构和功能,创建出用于连接输入端和输出端的神经元。每个神经元节点作为一个激励函数,传达不同数据之间的交流信息。节点之间的权重可类比于生物的记忆功能,通过不断的学习进而不断的更新,从而实现类似人一样的判断能力[16]。在样本数据足够完善的情况下,通过神经网络的训练学习可以很好的表达出一些复杂的、非线性的模型,因此可将神经网络模型用于滑坡易发性指数的回归。
2.2.3 支持向量机
支持向量机模型的思想是:将输入向量根据一定的法则映射到更高维数的特征空间,并在该特征空间构造一个最优分类面,利用最优分类面对数据进行分类或者回归,从而实现学习和预测的功能[17]。将支持向量机模型作为神经网络的对照模型,对比两个模型在相同训练集情况下的学习效果,筛选出合适的模型并计算评价结果。
3 滑坡评价因子量化结果
滑坡是一个复杂且非线性的系统,实验从滑坡的易发性角度出发[1],结合研究区概况和专家建议,选择了坡度、坡向、坡型、水系、岩组、高程和地形起伏共7 个因子。对于连续数据,首先通过自然断点法将数据分级,再利用频率比实现量化,而对于分类数据则直接利用频率比实现量化。量化结果如表2。

表2 因子量化结果Table 2 Results of factor quantification
考虑到各因子之间可能存在的相关性会对结果产生不利影响,在评价之前对量化的因子进行相关性分析,结果见表3。其中地形起伏因子和坡度、岩组、高程的相关性分别达到了0.61,0.25 和0.27,相关性过高。而剩余的六个因子之间相关性都低于0.2,所以实验选择剔除地形起伏因子,保留剩余的6 个因子作为南江县滑坡易发性的评价因子。

表3 因子相关性分析结果Table 3 Results of factor correlation analysis
为方便ArcGIS 成图,实验将每个因子的量化值扩大1 000 倍后取整,为每个等级因子配上不同的颜色以区分,结果见图2。

图2 因子量化结果Fig.2 Results of factor quantification
4 机器学习的应用
4.1 数据预处理
为消除数据之间的量纲不一致性,利用标准化操作对数据进行特征缩放,使其值落在[0,1]之间。实践证明,处理后的数据不仅能加快机器学习的收敛速度,同时还能提高模型整体精度,保障模型的稳定性和可行性。标准化公式如式(2)。
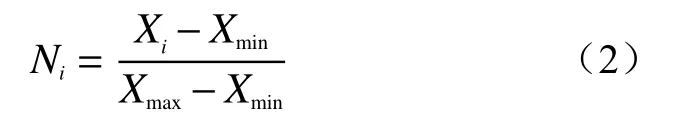
式中:Ni——Xi标 准化后的值;
Xi——因子X在二级属性i下的频率比值;
Xmin——Xi量化的最小值;
Xmax——Xi量 化的最大值。
4.2 样本选取
训练样本的质量决定着模型整体的稳定性,因此,在滑坡样本的选取上,实验将359 个滑坡点全部作为样本数据,以此来外推出符合滑坡性质的栅格点。在非滑坡样本的选取上,实验通过随机选择和通过k 均值聚类两种方法筛选非滑坡点。再将非滑坡点和滑坡点的数据整合到一起,以此获得完整的样本数据。
4.2.1 随机选取非滑坡点
实验通过随机选择研究区的点位作为非滑坡点,以此来和聚类的结果作为对照。将随机选择的1 000 个非滑坡点和359 个滑坡点整合,再打乱顺序,按照7∶3的比例分配训练集和测试集。
4.2.2 K 均值聚类选取非滑坡点
将因子标准化结果作为聚类的输入数据,采用k 均值聚类算法将原始数据分为五大类。为了挑选出非滑坡的样本点,将聚类结果和历史滑坡点进行叠加分析,结果如表4。统计聚类结果中滑坡所占的个数和滑坡所占的相对比例。选择滑坡所占个数最少且滑坡所占相对比例最低的聚类结果作为非滑坡的样本,由表中可知,聚类结果为2 的栅格满足要求,因此从该类中随机采样1 000 个点作为非滑坡点。同样将筛选出来的1 000个非滑坡样本和359 个滑坡样本整合,随机打乱顺序,按照7∶3 的比例分配训练集和测试集。

表4 k 均值聚类统计分析结果Table 4 Results of k-means clustering statistical analysis
4.3 神经网络模型的构建
通过反复对比实验,神经网络模型在构建时选择一个隐含层,且隐含层中设置13 个神经节点的效果较好。每个神经元的激活函数选择Logistic 函数,权重迭代器选择了基于随机梯度的优化器。将随机模型和k均值聚类模型生成的数据集分别作为神经网络模型的输入,保存训练好的两个模型以及相应的训练结果参数。
4.4 支持向量机模型的构建
支持向量机在模型构建时,在核函数上选择了能处理非线性特征的多项式核函数。同时将误差项的惩罚参数设置为1,通过验证该值能很好的提高模型的预测能力和泛化能力。同理,将随机模型和k 均值聚类模型生成的数据集分别作为支持向量机模型的输入,保存训练好的两个模型以及相应的训练结果参数。
4.5 模型精度验证及模型选择
上述的对照实验,一共保存了4 个模型,对应4 组精度验证曲线,分别为:(1)通过k 均值聚类算法筛选非滑坡点,以神经网络为训练模型,训练结果的ROC 曲线ANN_km。(2)通过k 均值聚类算法筛选非滑坡点,以支持向量机为训练模型,训练结果的ROC 曲线SVR_km。(3)通过随机筛选非滑坡点,以神经网络为训练模型,训练结果的ROC 曲线ANN_sj。(4)通过随机筛选非滑坡点,以支持向量为训练机模型,训练结果的ROC 曲线SVR_sj(图3)。
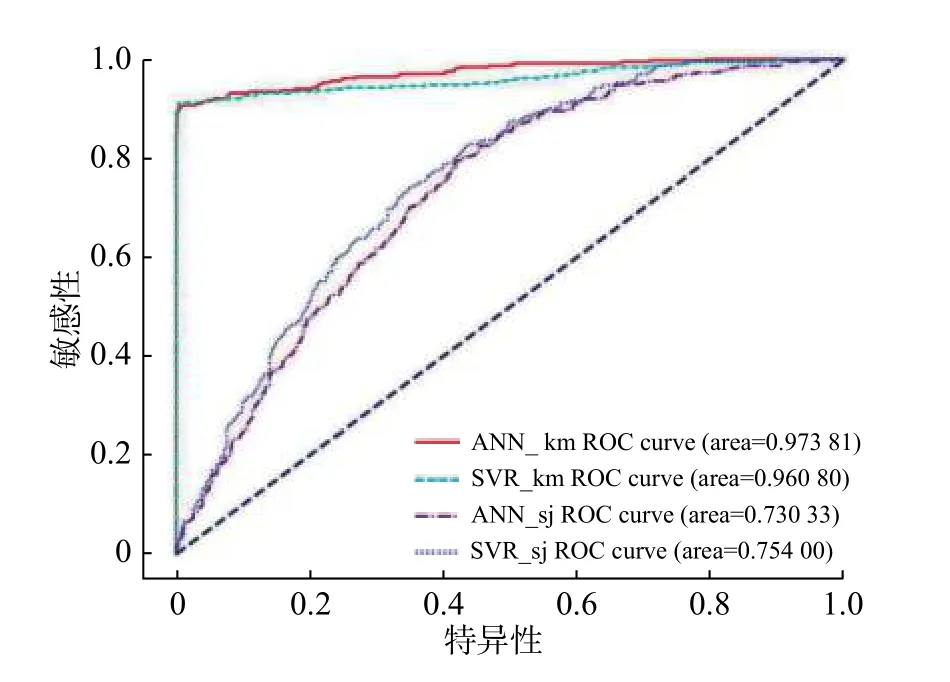
图3 训练集ROCFig.3 Training set ROC
为检验模型的稳定性和可靠性,将相应的测试集输入到训练好的4 个模型,同样也获得了对应的4 条ROC 曲线。分别为:ANN_km_t,SVR_km_t ,ANN_sj_t,SVR_sj_t(图4)。

图4 测试集ROCFig.4 Test set ROC
由结果可知,在随机筛选非滑坡样本的前提下,神经网络和支持向量机的训练精度约为70%,表明两个模型在一定程度上能反映滑坡的易发性指数。在k 均值聚类筛选非滑坡样本的前提下,神经网络和支持向量机的训练精度约为97%和96%,远高于随机模型下的训练精度,由此可知,k 均值聚类和两个回归模型的结合能够更好的反映滑坡的易发性指数。
对比训练集和测试集的ROC 曲线面积,在相同前提和模型下,训练集和测试集的精度基本相同,说明以上4 个模型都拥有稳定的预测和外推能力。其中在k 均值聚类的前提下,神经网络及支持向量机的训练集和测试集精度都高于95%,表明k 均值聚类和两个回归模型的结合不仅能很好的反映滑坡易发性指数,而且模型具有很好的稳定性、泛化性和外推性。实验最终选择了训练精度和稳定性都较高的k 均值聚类和神经网络的结合模型及k 均值聚类和支持向量机的结合模型作为评价的基础。
4.6 易发性分区
将研究区的所有栅格点数据分别输入到保存好的k 均值聚类—神经网络模型和k 均值聚类—支持向量机模型,以此获取不同模型下的易发性指数,再利用自然断点法根据易发性指数将南江县分为五个区域,分别为不易发、低易发、中易发、高易发和极高易发(图5)。其中图5(a)为在k 均值聚类结合神经网络模型得到的结果;图5(b)为k 均值聚类结合支持向量机模型获得的结果。两个模型所得到的分区结果在大体上相似,其中不易发和低易发区域集中出现在南江县北部区域。高易发和极高易发集中出现在南江县中部。

图5 易发性分区图Fig.5 Susceptibility zone map
为验证两个模型在南江县整个范围内的适用性,实验将两个模型得到的易发性分区图与历史灾害点叠加分析,通过相对滑坡频率比来验证模型精度,计算公式如式(3)。

式中:Ai——易发性分区i的相对滑坡频率比;
mi——易发性分区i下的滑坡个数;
si——易发性分区i的栅格个数;
N——研究区总滑坡个数;
S——研究区总栅格数。
神经网络模型的精度验证结果见表5,支持向量机模型的精度验证结果见表6。从结果中我们可以看出,不管是神经网络还是支持向量机,两个模型所得结果的滑坡点在不易发到极高易发的个数都是递增的,相应的相对滑坡比也是递增的。说明两个模型在研究区范围内具有稳定的适用性。其中神经网络在极高易发区的相对滑坡比高于支持向量机,在不易发的相对滑坡比低于支持向量机,这表明神经网络在全局上的精度高于支持向量机。

表5 神经网络分区统计结果Table 5 Partition statistics results of neural network

表6 支持向量机分区统计结果Table 6 Partition statistical results of support vector machines
从数据的直观性上我们可初步判定神经网络的精度优于支持向量机,为了更准确的反应两个模型的精度,实验用成功率验证曲线[18]来量化两个模型在全局的精度,其中横轴为根据易发性指数从高到低的累计栅格百分比,纵轴为历史滑坡累计发生频率(图6)。实验表明神经网络在全局的精度约为76%,支持向量机的精度约为74%。这也验证了上述由相对滑坡比所得到的结论。

图6 模型全局精度验证曲线Fig.6 Model's global accuracy verification curve
5 结论
(1)利用k 均值聚类筛选非滑坡样本,得到的结果用于神经网络和支持向量机两个模型的训练,其训练结果精度分别为97%和96%,远高于利用随机模型筛选滑坡时获得的训练精度。
(2)将k 均值聚类算法同神经网络结合,得到南江县的易发性分区图,其中从不易发到高易发分区所占的比例分别为35.24%、17.29%,19.51%,16.56%,11.39%。将k 均值聚类算法同支持向量机结合,得到了另一份南江县易发性分区图,其中从不易发到高易发分区所占的比例分别为29.74%,24.93%,21.96%,12.56%,11.11%。两个模型所得到的分区结果在大体上相似,其中不易发和低易发区域集中出现在南江县北部区域。高易发和极高易发集中出现在南江县中部。
(3)利用相对滑坡比作为模型的评价指标,其中神经网络在极高易发区的相对滑坡比高于支持向量机,在不易发的相对滑坡比低于支持向量机,这表明神经网络在全局上的精度高于支持向量机。为了量化模型的全局精度,采用成功率验证曲线,结果表明神经网络在全局的精度约为76%,支持向量机在全局的精度约为74%。

