基于Mein-Larson入渗模型的凹形边坡稳定性分析
胡 庆,吴益平,苗发盛,张龙飞,李麟玮
(中国地质大学(武汉)工程学院,湖北 武汉 430074)
0 引言
我国是一个地质灾害频发的国家,其中滑坡占地质灾害总数的51%以上[1]。研究表明,降雨与边坡失稳破坏紧密相关。降雨入渗会导致湿润锋下移,进而降低坡体的基质吸力,弱化岩土体参数,使坡体下滑力增大,抗滑力减小[2]。所以研究降雨作用下边坡的湿润锋分布规律,并在此基础上进行边坡稳定性分析是很有必要的。
国内外对于降雨入渗模型的研究,都是在1911年GREEN 等[3]提出Green-Ampt 模型的基础上改进的。例如,MEIN 等[4]考虑了降雨强度小于土体渗水能力情况下的GA 模型,即ML 模型。CHU[5]分析了地表有积水和无积水的降雨入渗情况。PHILIP[6]对于具有初始水头的均匀各向同性的均质土壤的平面斜坡渗透问题,给出了非线性不饱和渗流方程的解。MUNTOHAR 等[7]考虑了土体的非饱和特性。饶鸿等[8]提出了以含水率为变量的抗剪强度公式。常金源等[9]研究了考虑动水压力的浅层滑坡的Green-Ampt 模型,提出了边坡饱和的临界时间。李秀珍等[10-11]改进了原有的Mein-Larson 模型,研究了考虑饱和土、非饱和土等边坡的稳定性以及失稳破坏概率。孟庆成等[12]分析了水力滞回性对边坡稳定性的影响。王进等[13]考虑了水对岩土参数的弱化作用,提出了坡面供水强度以及入渗能力的概念。唐扬等[14]考虑了初始含水率与深度呈线性关系的情况。然而这些模型都是基于直线形态的边坡进行分析的,没有考虑边坡为曲线形态的情况。事实上对于实际的边坡,曲线形态的边坡占88%左右[15],而边坡表面的应力分布情况很大程度上受坡面形态的影响[16]。所以开展曲线形态的边坡降雨入渗规律研究和稳定性分析是十分必要的。
鉴于此,文章基于降雨入渗基本理论,将Mein-Larson入渗模型和坡形函数相结合,探究凹形边坡在高强度和低强度两种降雨条件下的入渗规律,并结合极限平衡分析方法,推导凹形边坡稳定性计算方法。按照坡形拟合以及坡形简化的思路,将实际边坡考虑成凹形边坡和直线坡进行稳定性计算,并与数值模拟分析对比,对上述模型进行验证。
1 凹形边坡降雨入渗模型
1.1 坡形函数
目前主要通过指数、对数和双曲线三类函数来描述坡面形态。为了研究方便,假定边坡几何满足指数函数,建立以坡形中点为原点的全局坐标系,则坡形函数可表示为[17]:
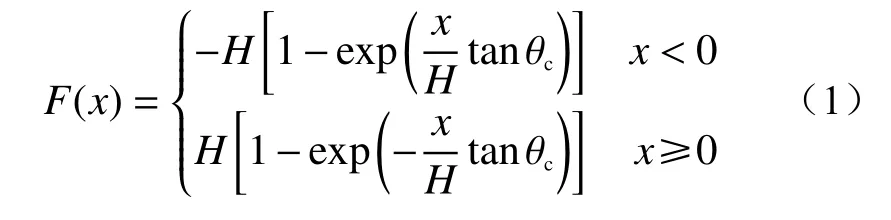
式中:θc——最大等效坡角;
H——边坡等效高度。
边坡表面曲线如图1所示。
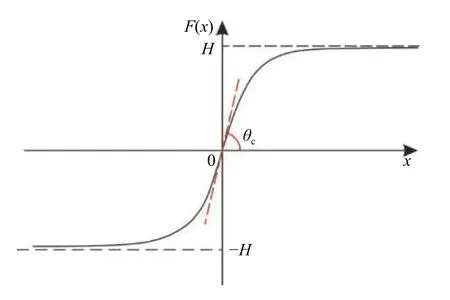
图1 坡面函数曲线Fig.1 Slope function curve
对于任意一点P(x,y),可以得到该点的切线斜率f(x)为:
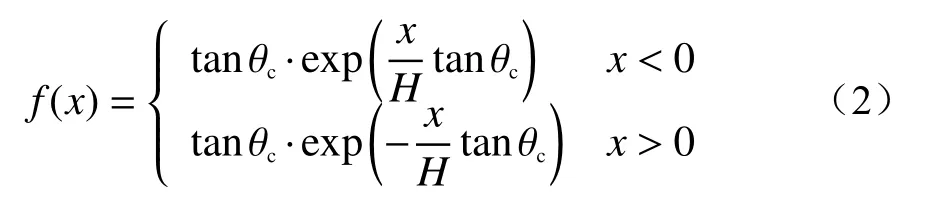
将点P的切线和水平方向间的角度记作β,即点P的等效坡角,则

因此对于坡面任何一点P,可以根据数学关系确定该点的等效坡角β。
1.2 凹形边坡降雨入渗模型
针对已提出的Mein-Larson 模型,可以总结出降雨入渗的规律曲线如图2所示。
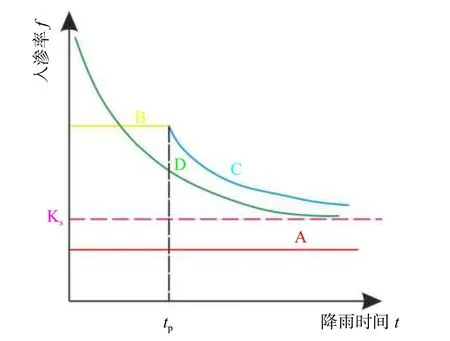
图2 降雨入渗规律曲线Fig.2 Rainfall infiltration law curve
假定降雨强度为p,饱和渗透系数为Ks,土体渗水能力为fp。
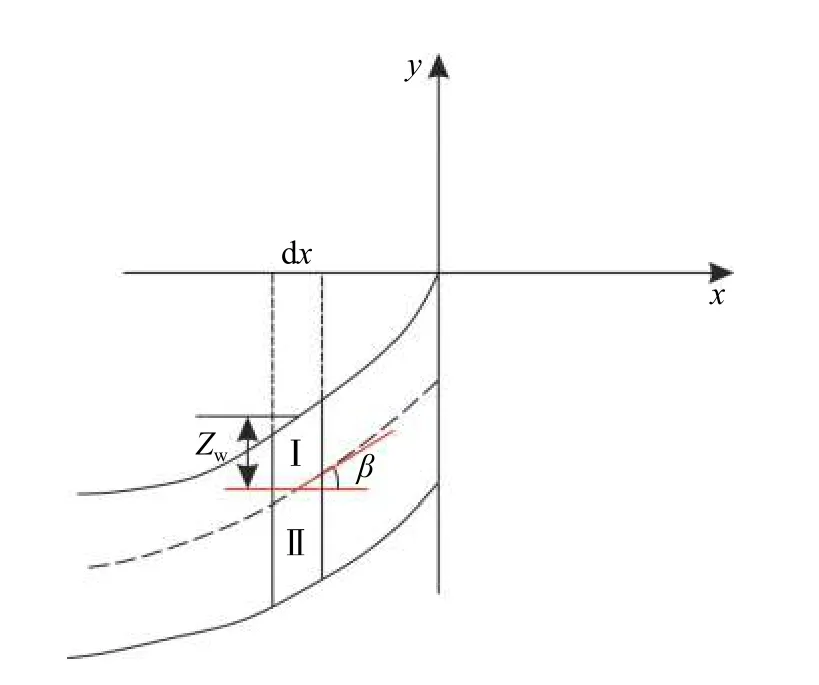
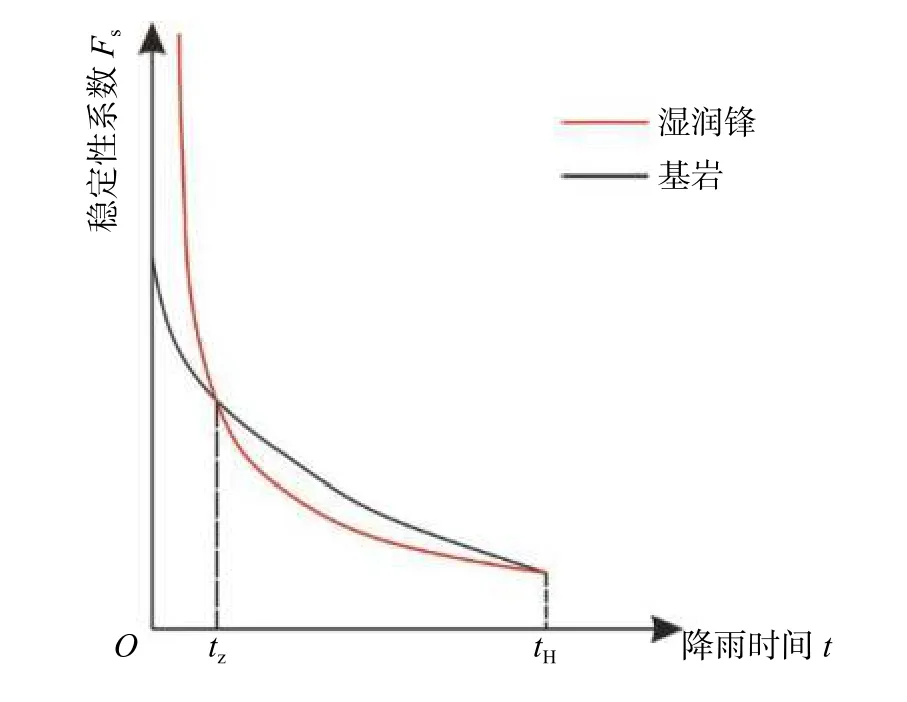
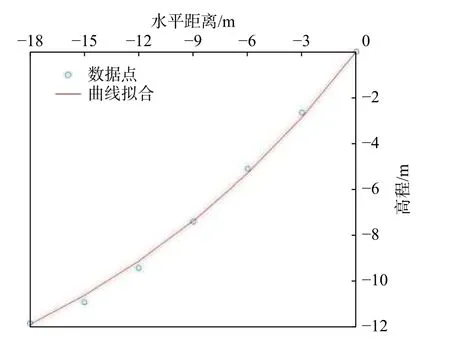
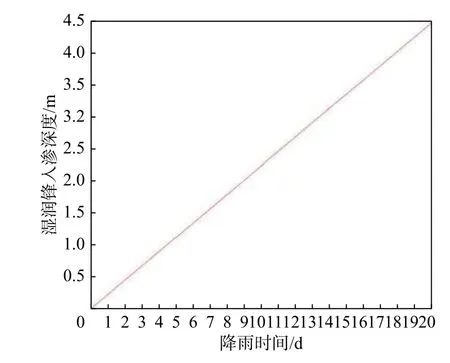
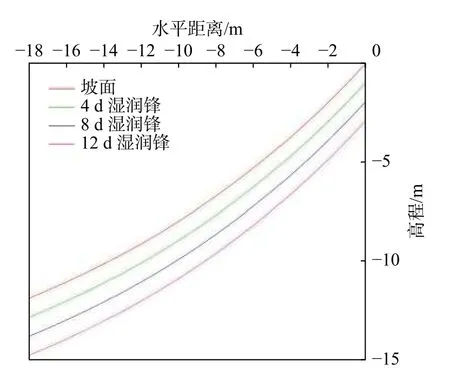
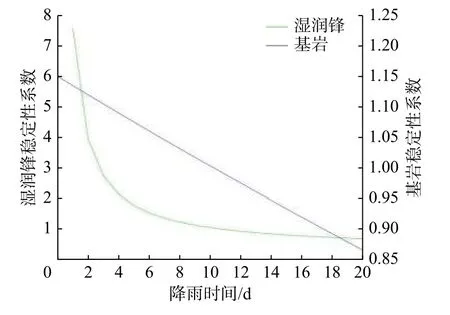
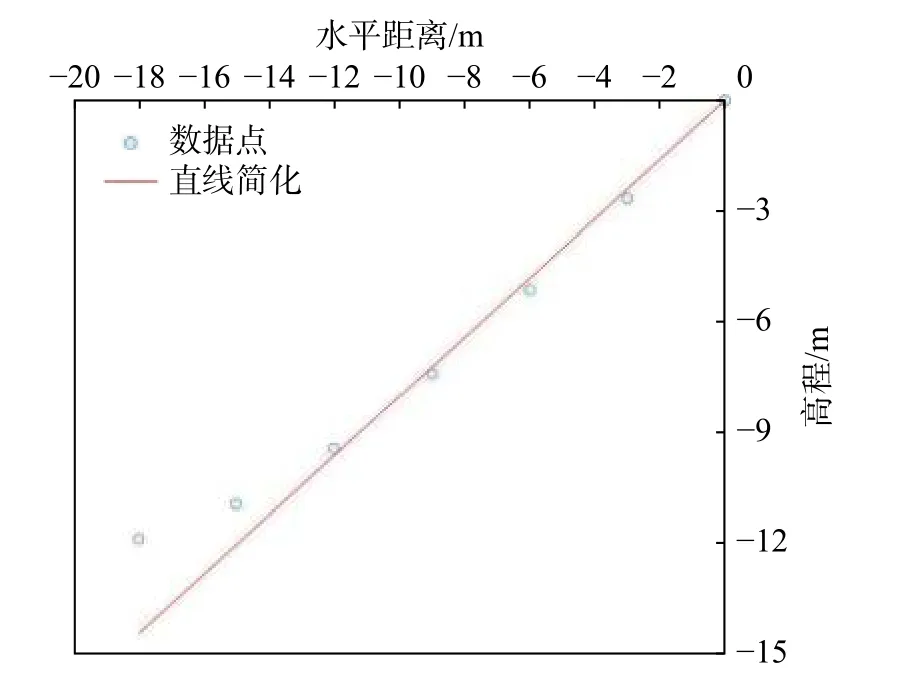
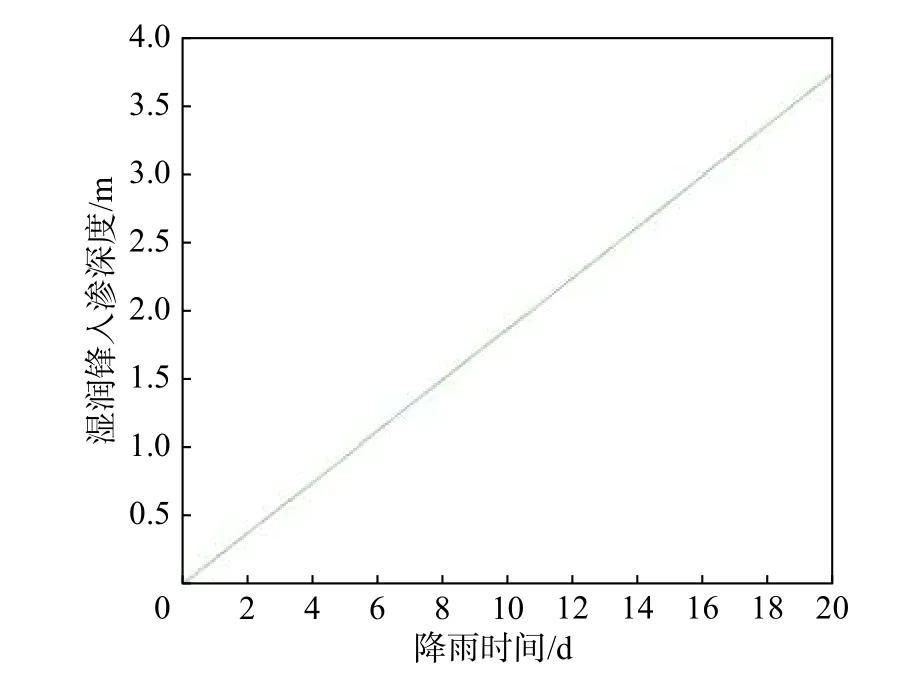
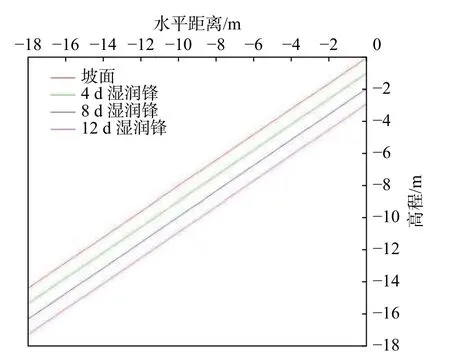
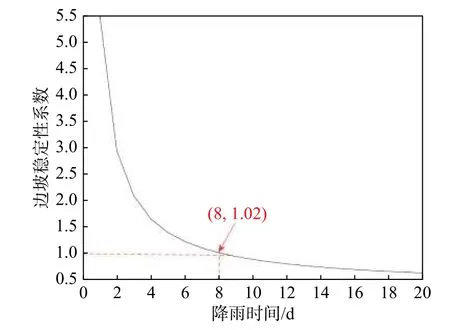
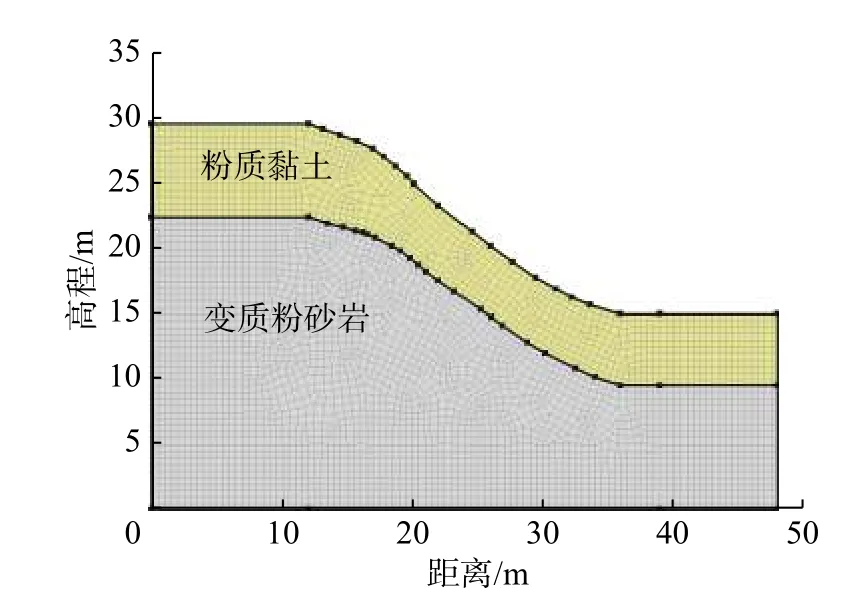
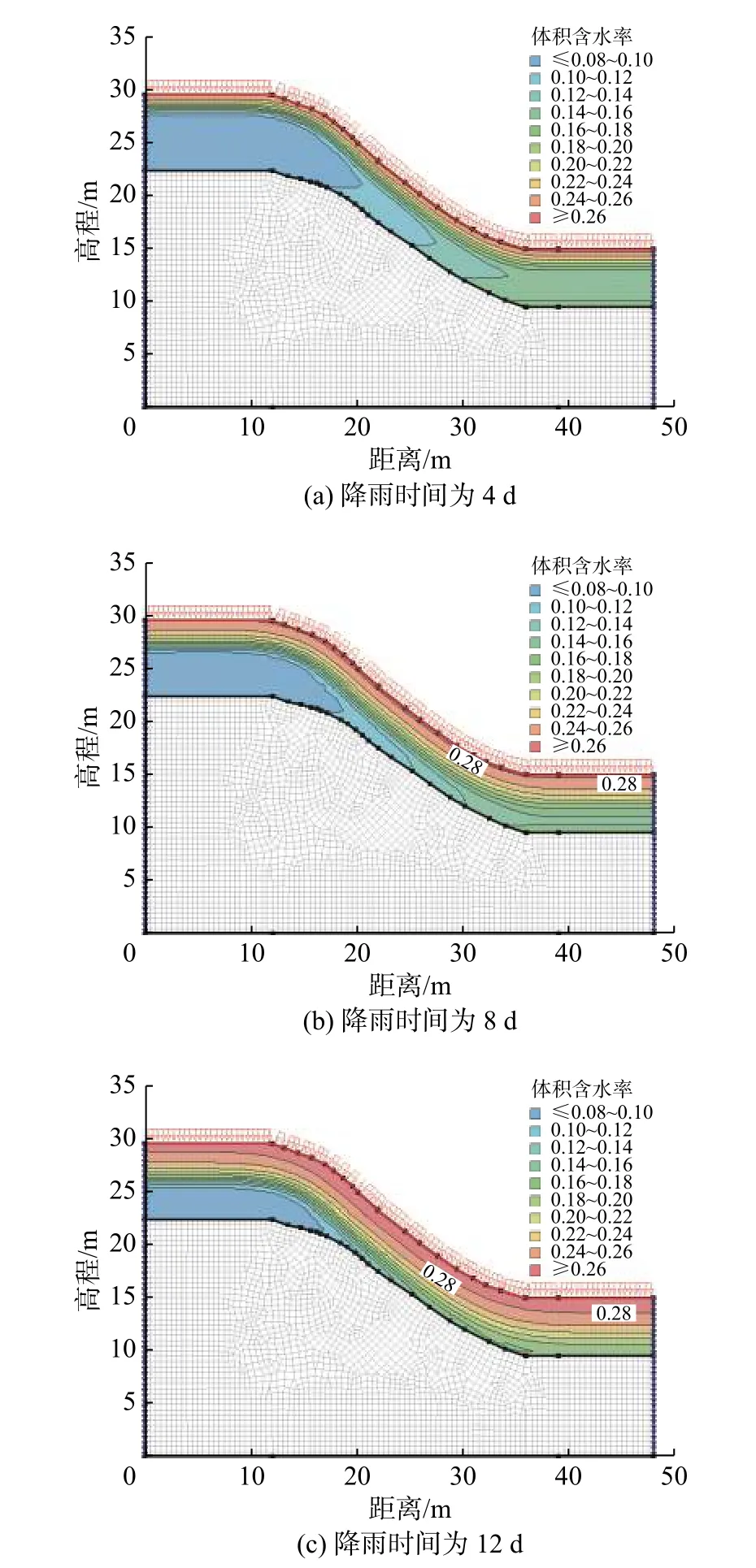
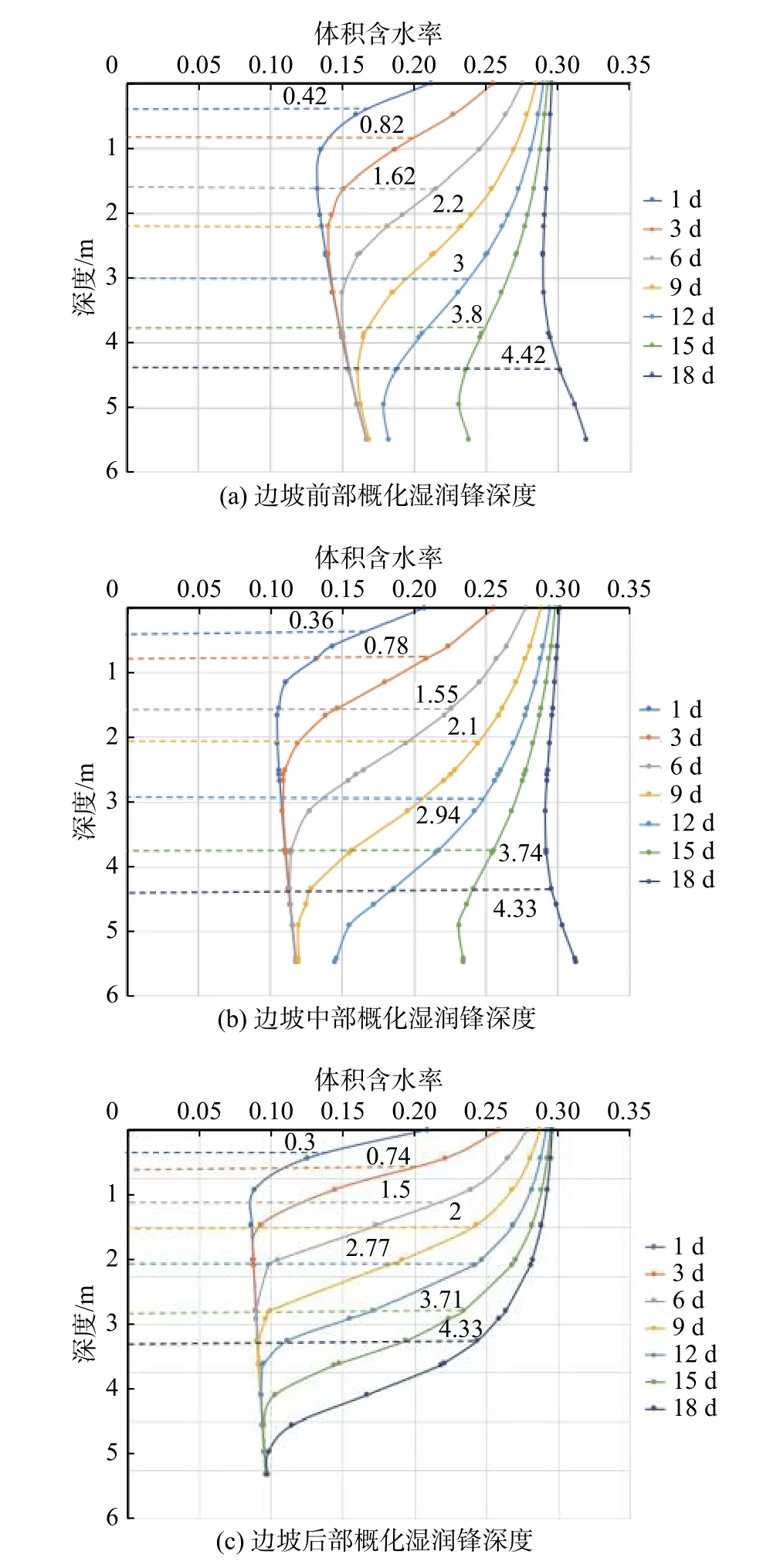
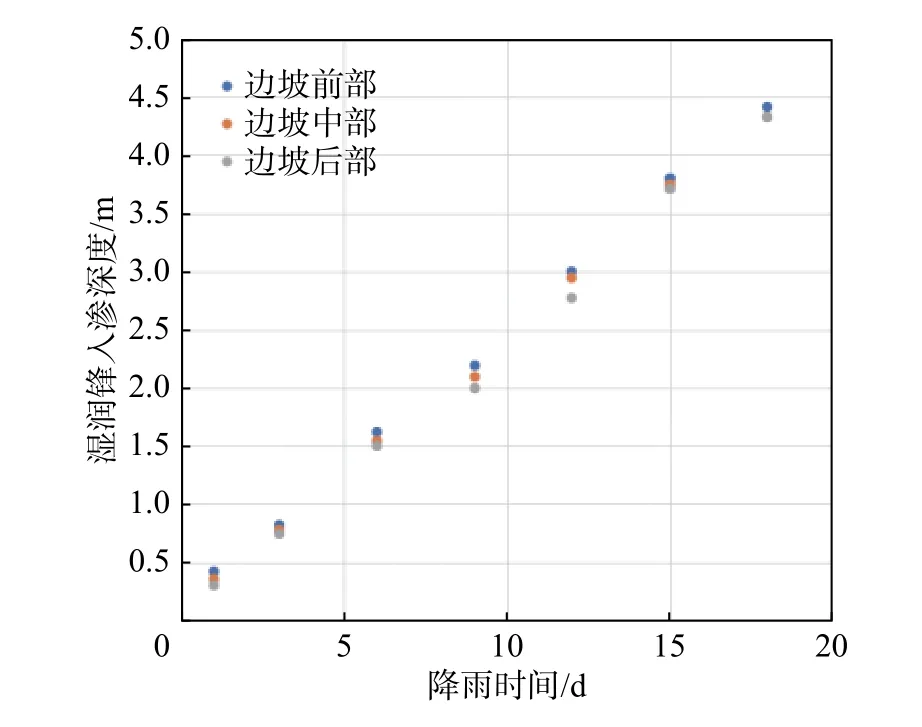
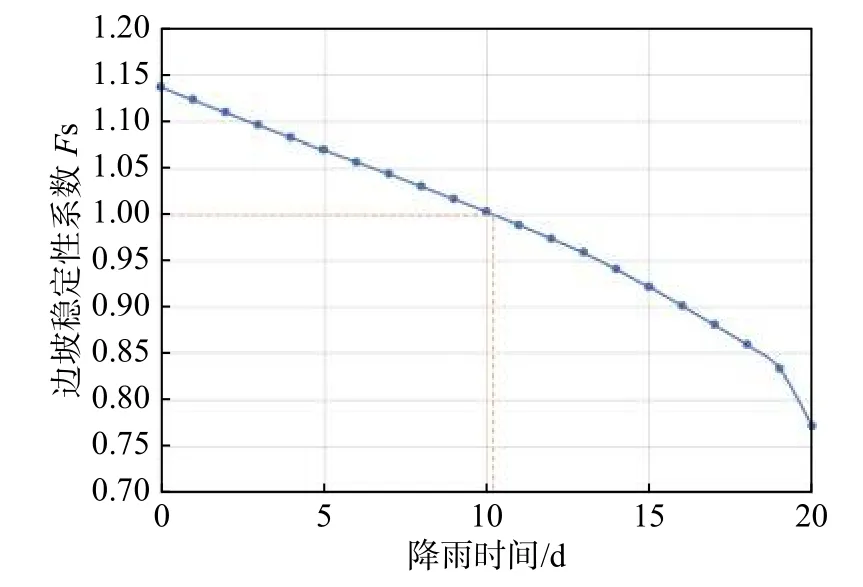
事件A:低强度降雨条件下,p 事件B:p 事件C:Ks 大多数的降雨情况可能是在积水状态下的恒定降雨强度的降雨入渗,如曲线D 所示,其中ts表示初始状态为积水时的降雨入渗下,其累积的降雨量达到Ip所用的时间。 因此针对于凹形边坡降雨入渗模型,本文根据降雨入渗规律,主要从恒定降雨条件下的两种情况来进行介绍。 对于凹形边坡,先考虑边坡上任意的一点P(x,y)的降雨入渗,做出其降雨入渗的计算简图(图3)。 图3 降雨入渗模型计算简图Fig.3 Calculation diagram of rainfall infiltration model 图中:p——降雨强度; X*——点 P 沿边坡向下的切线方向; Z*——点P垂直切线指向坡体内部的方向; θs——P点处土体饱和体积含水率; θi——P点的初始体积含水率; β——点P的等效坡角。 (1)高强度降雨时(p>Ks) 当t小于积水时间tp时,即图2中的线段B。此时降雨累积入渗量Ip为: 积水时间tp为: 当时间t大于积水时间tp时,此时降雨累积入渗量I为: ts是初始状态为积水的降雨情况下,总入渗量I=Ip花费的时间,则ts为: 综上所述,可以得到各时段Z*方向湿润锋的入渗深度为: (2)低强度降雨时(p 此时雨水都进入土体中,累积入渗量I为: 同理可以求得Z*方向湿润锋的入渗深度为: 值得注意的是,当等效坡角不变时,以上公式即为坡面形态为直线的Mein-Larson 模型。 当点P变化时,P点的等效坡角也在变化,其湿润锋深度也随之变化。当坡面某入渗点确定时,其湿润锋深度也唯一确定。因此可以通过具体坡形函数来确定任意一点的等效坡角,并根据以上公式得到任意一点湿润锋的入渗深度,从而探究凹形边坡的降雨入渗规律,计算过程可以通过Matlab 编程来实现。 在进行稳定性公式推导前,对该凹形坡作如下假设: (1)边坡下部基岩为微透水或不透水,且基岩面近似与坡面平行; (2)边坡物质为均质体,满足各向同性; (3)地表无积水产生,即地表水头h=0。 为了求出凹形边坡在恒定降雨条件下的稳定性计算公式,将边坡等分成n块,每块间距为dx。任取某块边坡进行分析(图4),湿润锋以上部分为区域Ⅰ,湿润锋以下部分为区域Ⅱ。区域Ⅰ的坡体已经全部饱和,区域Ⅱ的坡体仍处于天然状态。 图4 边坡稳定性计算示意图Fig.4 Schematic diagram of slope stability calculation 计算边坡的稳定性系数时,对于任意一块坡体的湿润锋竖直入渗深度,取该块坡体两端点湿润锋竖直入渗深度的平均值,记为ZW,其坡角为两端点等效坡角的平均值,记为β。对于区域Ⅰ的坡体,采用浮重度γ´进行计算,对于区域Ⅱ的坡体,采用天然重度γt进行计算。 对所取块体进行力学分析,区域Ⅰ的抗滑力、下滑力和渗透力分别为: 区域Ⅱ的抗滑力和下滑力分别为: 式中:dW1——区域Ⅰ的重力; dW2——区域Ⅱ的重力。 其分别为: 式中:c´,φ´——饱和状态下的黏聚力和内摩擦角; c,φ——天然状态下的黏聚力和内摩擦角; γw——水的重度; Zw——该块坡体竖直方向上的湿润锋深度,且Zw=Z*f/cosβ; 其他参数意义同上。 因此区域Ⅰ整体的抗滑力、渗透力以及下滑力可以通过条块求和获得,记为: 区域Ⅱ整体的抗滑力以及下滑力可以通过条块求和获得,记为: 对于本文研究的凹形边坡,其潜在滑移面的确定应该分别从湿润锋与基岩面两处展开分析,通过比较两者稳定性系数大小来判断滑移面可能存在的位置。 下面讨论凹形边坡滑移面的两种形式: (1)当在湿润锋面发生滑移: 式中:FS1——湿润锋处的稳定性系数。 (2)当在基岩面发生滑移: 式中:FS2——基岩处的稳定性系数。 做出凹形边坡两种稳定性的关系图如图5所示。当降雨时间小于tz时,湿润锋的入渗深度接近于0,因此湿润锋处稳定性系数接近于无穷大,而此时基岩稳定性系数是某一定值,此时边坡稳定性系数以基岩为主;当降雨时间大于tz时,边坡稳定性系数以湿润锋为主。随着降雨时间的增加,湿润锋入渗深度不断增大,直到几乎接近基岩面(t=tH时),此时两者的稳定性系数相同。 图5 稳定性系数变化曲线Fig.5 Variation curve of stability coefficient (1)高强度降雨时(p>Ks) 此时湿润锋的深度由公式(14)确定,在确定了湿润锋的深度后,结合上文提出的凹形边坡稳定性计算公式,运用Matlab 编程得出基岩和湿润锋的稳定性与降雨时间的关系,从而实现凹形边坡的稳定性评价。 (2)低强度降雨时(p 此时湿润锋的深度由式(16)确定,在确定了湿润锋的深度后,结合上文提出的凹形边坡的稳定性计算公式,运用Matlab 编程得出基岩和湿润锋的稳定性与降雨时间的关系,从而实现凹形边坡的稳定性评价。 选取四川省阿坝州松潘县某工程边坡为例[18],对边坡的稳定性进行理论探讨。边坡所在区域为岷山山脉中部,地形以高中山为主,气候呈现地域性变化的特点,而且该区域降雨分布不均匀,夏季的降雨量占全年的80%,日最大降水量为50 mm,持续时间最长为22 d。因此假定降雨强度为0.048 m/d,持续降雨20 d。边坡岩土体相关参数主要来源于参考文献[18](表1)。 表1 边坡岩土及水文参数表Table 1 Geotechnical and hydrological parameters of slope 按照坡形拟合以及坡形简化的思路,将实际边坡分别考虑成凹形边坡与直线边坡进行降雨入渗规律研究与稳定性计算,对本文推导的凹形坡稳定性计算模型与传统斜坡稳定性计算模型进行分析对比。 3.1.1 凹形边坡稳定性计算 选取实际边坡(即边坡数值模型18~36 m 区段)表面的特征点,基于Matlab 软件,用坡形函数对坡面特征点进行拟合,拟合效果如图6所示。从图6可以看出,坡形函数能较好地拟合出实际边坡的坡面形态。 图6 坡面与水平距离关系曲线Fig.6 Relationship curve between slope and horizontal distance 基于上文的凹形边坡入渗模型,利用Matlab 编程软件,可以得到边坡湿润锋入渗深度与时间关系曲线(图7)、不同降雨时刻(取4 d、8 d、12 d)湿润锋与坡面相对位置(图8)、以及凹形坡稳定性系数和时间的关系(图9)。 图7 湿润锋入渗深度随时间变化曲线Fig.7 Variation curve of wetting front depth with time 图8 不同降雨时刻湿润锋面与坡面的关系图Fig.8 The relationship between wetting front and slope at different rainfall time 对图7、图8分析可知,湿润锋入渗深度与时间呈正比关系,最大入渗深度为4.47 m,而且湿润锋面为凹线形态,与坡面平行。 从图9可以看出,在降雨初期,湿润锋稳定性系数较基岩大,当降雨时间等于10 d 时,基岩稳定性系数为1.004,而湿润锋稳定性系数为1.07,稳定性以基岩为主,根据《滑坡防治工程勘查规范》 (GB/T32864—2016),此时凹形边坡为欠稳定状态;继续降雨,边坡稳定性系数小于1,会发生失稳破坏。 图9 边坡稳定性系数随时间变化曲线图Fig.9 Curve of slope stability coefficient with time 3.1.2 直线边坡稳定性计算 基于Matlab 软件,将实际边坡(即边坡数值模型18~36 m 区段)的坡面形态直接简化成直线坡,实际边坡简化效果如图10所示。从图10可以看出,单纯对坡面形态进行简化,会使得研究对象发生“失真”的情况,此时等效坡角的正切值恒为0.8。 图10 坡面与水平距离关系曲线Fig.10 Relationship curve between slope and horizontal distance 基于上文的凹形边坡入渗模型,当等效坡角恒定不变时,利用Matlab 编程软件,可以得到边坡湿润锋入渗深度与时间关系曲线(图11)、不同降雨时刻(取4 d、8 d、12 d)湿润锋与坡面相对位置(图12)。 图11 湿润锋入渗深度随时间变化曲线Fig.11 Variation curve of wetting front depth with time 图12 不同降雨时刻湿润锋面与坡面的关系图Fig.12 The relationship between wetting front and slope at different rainfall time 从图11可以看出,湿润锋入渗深度与时间呈正比关系,最大入渗深度为3.75 m,比凹形边坡的湿润锋最大入渗深度小。从图12可知,随着降雨的持续,边坡的湿润锋面为直线形,始终与坡面平行。 根据文献[9]中浅层斜坡滑动稳定计算模型,可以得到直线边坡的稳定性系数如图13所示。从图13可以看出,随着降雨时间的增加,边坡稳定性系数逐渐减小,当降雨时间等于8 天时,边坡的稳定性系数为1.02,根据《滑坡防治工程勘查规范》 (GB/T32864—2016),此时直线边坡为欠稳定状态;继续降雨,边坡稳定性系数小于1,会发生失稳破坏。其稳定性系数比实际边坡当作凹形边坡分析得到的稳定性系数小。 图13 边坡稳定性系数随时间变化曲线图Fig.13 Curve of slope stability coefficient with time 3.2.1 边坡数值模型建立 根据实际边坡,建立边坡数值模型(图14),其中上层为粉质黏土,下层为变质粉砂岩,地下水位线位于坡脚以下2.5 m 处,在模型两侧设置定水头边界,降雨边界设定参照文献[19]。 图14 边坡数值模型Fig.14 Numerical model of slope 3.2.2 数值模拟分析 运用GeoStudio 的SEEP/W 模块对边坡开展渗流模拟,首先设定边界条件,实现边坡稳态模拟,得到瞬态分析的初始状态,并在坡体上边界设定0.048 m/d 的单位流量,持续降雨20 d。 湿润锋入渗深度变化可以通过土体含水率梯度的变化来表征,因此可以通过含水率的等值线云图大致判断湿润锋的变化规律[20],取降雨4 d、8 d、12 d 的含水率等值线云图(图15)。 从图15可以看出,随着降雨的持续,土体含水率因为雨水的进入而不断增加,且含水率的等值线与坡面近似平行,根据湿润锋与含水率梯度的关系,可以推断出湿润锋面应该与坡面近似平行,且湿润锋面为凹线形态,更加符合将实际边坡当作凹形边坡分析时的降雨入渗规律。 图15 不同降雨时长下边坡的体积含水率等值线云图Fig.15 Contour nephogram of volume moisture content of slope under different rainfall duration 为了进一步得到湿润锋的深度随着降雨时间的变化,本文设置了边坡前部、中部、后部三个含水率的监测剖面,记录了降雨时间为1 d、3 d、6 d、9 d、12 d、15 d、18 d 时含水率随深度的变化曲线,并根据文献[20]中概化湿润锋深度的判定方法,得到了不同降雨时间下边坡前、中、后部概化湿润锋的深度(图16)。 从图16中可以发现,在降雨初期,边坡表面含水率急剧增加,而坡体内部含水率接近于初始含水率,随着降雨时间的增加,雨水不断下渗,坡体内部含水率不断增大。同一降雨时间下,边坡前部湿润锋深度最大,中部湿润锋深度其次,后部最小,这是因为在降雨时,水进入土体的同时,会因为重力势能的作用向坡体前部流动,这也符合实际情况。 图16 不同降雨时间下边坡不同部位的概化湿润锋深度Fig.16 Generalized wetting front depth at different parts of slope under different rainfall time 根据以上分析绘制出在边坡前、中、后部概化湿润锋深度与时间的关系见图17。湿润锋入渗深度和时间成正比关系,湿润锋最大入渗深度为4.35 m,这跟将实际边坡当作凹形边坡分析时的湿润锋入渗深度更接近,表明本文提出的改进Mein-Larson 模型能够较为准确地描述凹形边坡的降雨入渗规律。 图17 边坡不同部位的湿润锋入渗深度随时间的变化曲线Fig.17 Variation curve of infiltration depth of wetting front with time in different parts of slope 在上文SEEP/W 瞬态分析基础上,在边坡后部以及前部设置滑移面进出口,并输入边坡岩土数据,运用GeoStudio 的SLOPE/W 模块,并基于Morgenstern-Price方法对凹形边坡开展稳定性分析,得出降雨强度等于0.048 m/d 时凹形边坡稳定性系数和时间关系见图18。 图18 边坡稳定性系数随时间变化曲线Fig.18 Variation curve of slope stability coefficient with time 对图17分析得出,随着降雨的持续,实际边坡的稳定性系数逐渐减小。当连续降雨10 d 后,稳定性系数减小到1.003,这与凹形边坡的稳定性计算得出的结果(1.004)十分接近,相对误差不超过0.1%,而此时直线边坡的稳定性系数早已小于1,进一步佐证了将实际边坡当作凹形边坡进行分析时,其稳定性计算结果更符合实际。 综上所述,通过本文计算模型中的坡形函数来拟合实际边坡的坡面形态,所得到的研究对象更符合实际。同时相对于浅层斜坡模型的计算结果,本文推导的凹形坡降雨入渗与稳定性计算模型的分析结果与数值模拟的分析结果更接近,表明本文的模型计算结果更符合实际情况,可靠性更高。 (1)通过对实际边坡的湿润锋分布规律进行研究发现:采用坡形简化得到的湿润锋最大入渗深度为3.75 m,采用坡形拟合得到的湿润锋最大入渗深度为4.47 m,更接近于边坡数值模拟得到的最大概化湿润锋深度4.33 m。表明推导的凹形坡降雨入渗模型更贴合实际入渗情况。 (2)在低强度降雨条件下,相比浅层斜坡计算模型,文章采用凹形坡稳定性模型计算的结果与数值模拟分析的结果更接近,其相对误差不超过0.1%,表明该模型可靠度较高;同时该模型不仅考虑了边坡表面形态的影响,而且考虑了边坡可能发生的两种破坏模式,具有计算简便,应用范围更加广泛的特点。 (3)提出的降雨入渗模型,当等效坡角β 恒定时,该模型就变为一般的Mein-Larson 降雨入渗模型。表明一般的Mein-Larson 降雨入渗模型是本模型的一种特殊情况。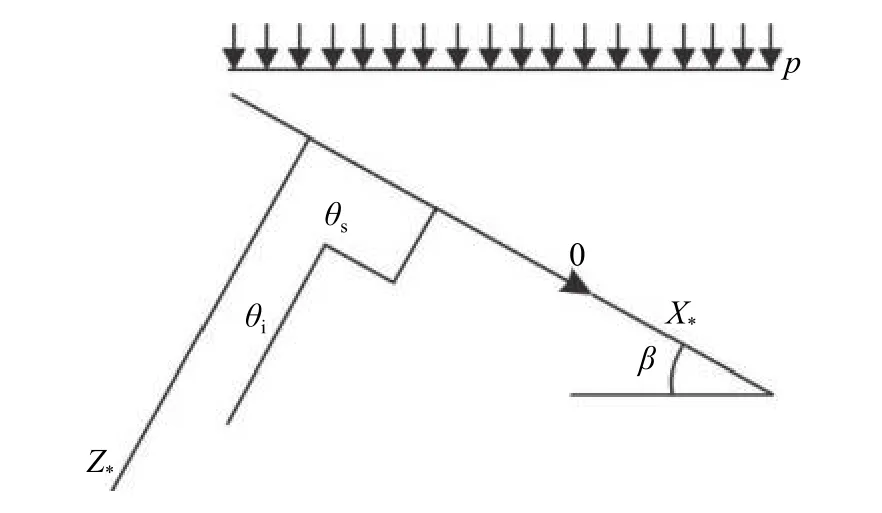
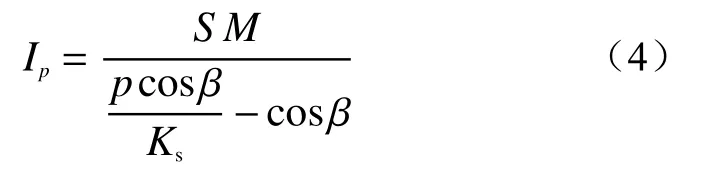

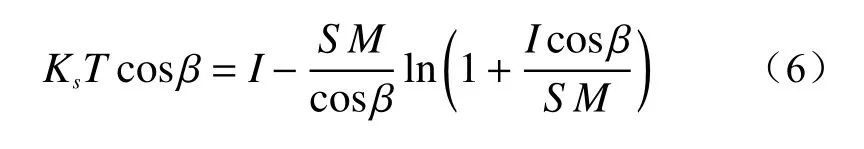
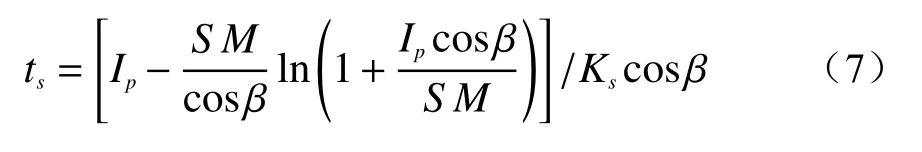
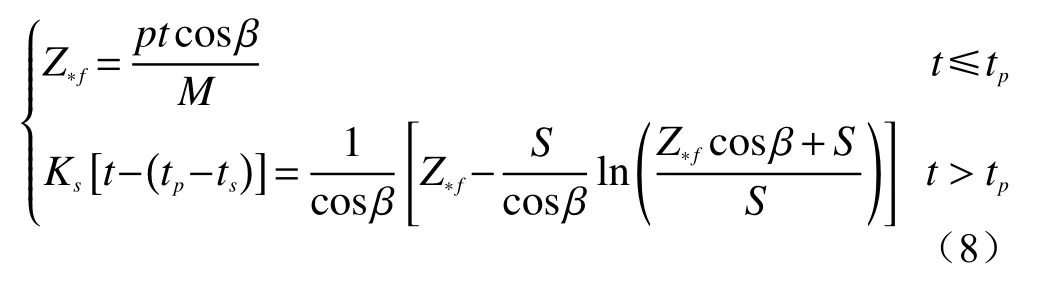


2 凹形边坡稳定性计算方法
2.1 凹形边坡稳定性计算公式
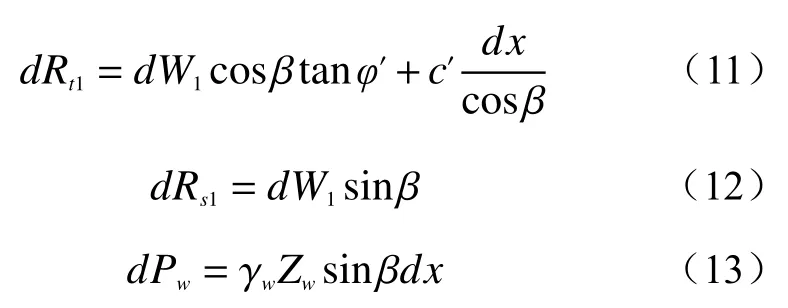
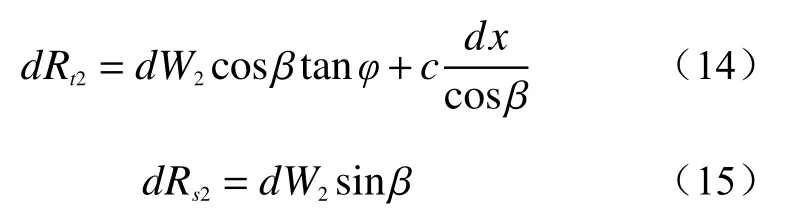
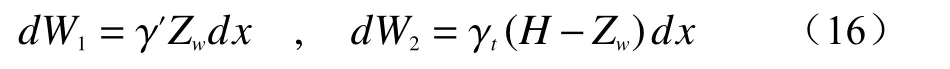
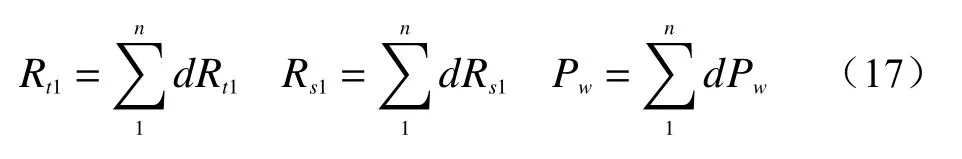
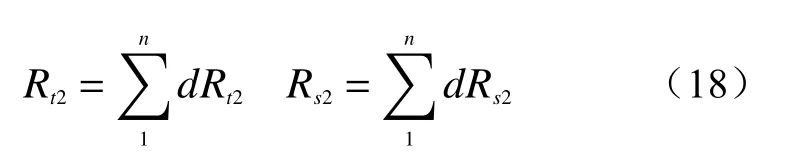
2.2 凹形边坡破坏模式分析

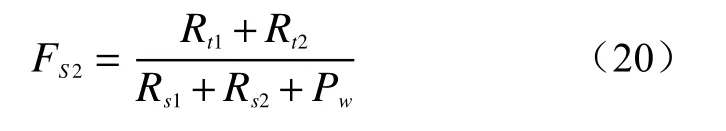
2.3 两种降雨条件下的稳定性分析
3 实际边坡降雨入渗规律与稳定性研究

3.1 实际边坡入渗规律研究以及稳定性分析
3.2 数值模拟分析
4 结论

