基于深度门控循环单元网络的转辙机健康状态评估

尹 航，梁玉琦，王成龙

(1.兰州交通大学 光电技术与智能控制教育部重点实验室，甘肃 兰州 730070；2.兰州交通大学 国家绿色镀膜技术与装备工程技术研究中心，甘肃 兰州 730070)

转辙机是铁路信号设备的关键部分，负责转换列车运行线路。但转辙机工作在室外，经常受到恶劣天气的影响，故障发生率较高。据我国某铁路局统计，近年来转辙设备故障约占全部铁路信号设备故障的39%[1]。因此，亟需对转辙机状态进行准确评估，利用从信号监测系统中得到的具有历史和持续退化趋势的数据，提取其单域或多域特征，构建健康指数HI，预测设备的健康状态。

健康指数HI最初被用于航空航天与军事系统的健康管理领域，对航天设备的健康状态进行实时估算。随着近年来铁路行业专注于设备的基于状态的维修，已经将HI应用于铁路基础设备的故障预测中[2]。本文亦用HI定义转辙机的健康状态，其范围为[0,1]。当HI值为0时，表明转辙机为最理想状态，能够正常完成转换铁路线路工作；当HI值逐渐增大时，设备损伤程度随之增大，进入退化过程；当HI值增加到1时发生故障，需要进行停机检修。HI值的构造在转辙机故障预测中起着至关重要的作用，不仅可以简化预测模型，而且能够产生比单一特征更好的预测结果，因此可以根据HI评估设备的健康状态，从而进行有计划的设备维护，降低安全隐患[3]。

文献[4]通过提取转辙机的时域特征并计算特征的单调性、趋势性、鲁棒性选择合适的特征，将最优特征子集作为自关联核回归的输入进行特征融合，得到HI，然后利用HI预测转辙机的剩余使用寿命。文献[5]通过对状态监控中的转辙机扳动力数据进行预处理，利用基于权值似然的混合特征评估和选择算法，以及基于最小特征散度权值的融合算法，构造了一个通用HI。文献[6]提出了一种基于支持向量描述(SSVD)的转辙机健康状态评估方法，利用SSVD建立健康指数实现对转辙设备的健康管理。文献[7]利用Kohonen神经网络对转辙机非故障功率数据进行聚类，然后利用隐马尔科夫模型识别出转辙机所处的健康状态。文献[8]利用自适应特征融合算法对筛选特征进行融合构建HI，并利用时间序列分割算法完成了对转辙机健康状态的划分。此外还有学者利用AdaBoost、SSBP、CCD、PCA等方法对转辙机进行状态监控及故障预测[9-12]。

上述文献主要针对于转辙机不同信号的时域特征进行处理。虽然时域特征能够从波动性、分散程度等方面反映转辙机的退化程度[13]，但是由于转辙机功率曲线具有非线性、非平稳的特点，所以处于不同状态时特征尺度也会有明显的差别。而集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)能够对非平稳信号进行分析，并且可以准确地提取特征时频域信息[14-15]。因此本文将时域特征与EEMD多尺度模糊熵相结合，利用不同域特征提取的方式对转辙机转动过程中产生的时序信号进行分析；然后通过局部加权回归LOESS获取特征重要趋势，并计算特征的单调性、相关性、鲁棒性，以选择合适的特征；最后输入深度门控循环单元(Gated Recurrent Unit, GRU)模型完成健康指数的构建，通过对比误差指标、预测准确率等验证该模型在转辙机健康状态评估上的有效性。

1 特征提取

1.1 时域特征提取

表1 时域特征表达式

1.2 EEMD分解

经验模态分解(EMD)是一种能够处理平稳和非平稳信号的自适应时频分析方法，它表明任何一个信号都是由多个IMF构成，每个IMF分量都包含了原始信号不同尺度的局部特征。在EMD分解过程中，每个IMF必须满足2个条件：①极值点数量和过零点数量应相等或相差最多1个；②在曲线上任意一点，局部极大值和局部极小值的包络均值为零。对于原始信号X(t)，其EMD表达式为

(1)

式中：Ci(t)为IMF分量；R(t)为残差。

由于信号极值点可能存在分布不均匀的现象，IMF分解时会发生模态混叠，即一个IMF会包含不同时间尺度的特征成分，因此HUANG等[16]提出了一种噪声辅助数据分析方法(NADA)，即向原始信号中加入频谱均匀分布、均值为零的高斯白噪声进行辅助分析，通过多次聚合添加噪声的IMF分量使噪声相互抵消、信号均匀分布到合适的参考尺度，并取聚合均值的结果作为最终结果。EEMD分解步骤如下：

Step1对于原始信号X(t)，初始化迭代次数m=1，聚合总次数为M，高斯白噪声幅值系数k∈[0.05σ,0.4σ]，σ为原始信号幅值的标准差。

Step2第m次聚合时，在原始信号中加入随机高斯白噪声wm(t) ，可得

Xm(t)=X(t)+kwm(t)

(2)

式中：Xm(t)为加入了M次白噪声的信号。

Step3对Xm(t)进行EEMD分解，得到n个IMF分量和一个剩余分量，即

(3)

式中：Ci,m(t)为第m次分解得到的第i个IMF；Rm(t)为剩余分量。

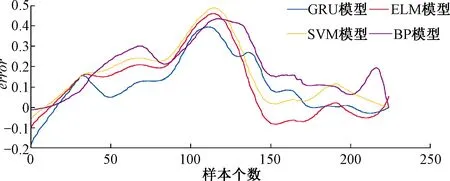
Step4当m

Step5计算M次聚合得到的各IMFs的均值Ci为

(4)

Step6取Ci作为最终的固有模态函数。

1.3 多尺度模糊熵特征提取

样本熵是衡量信号时间序列复杂度的物理量。但由于样本熵等特征提取方法对阈值参数具有很强的依赖性，模式距离在阈值附近出现微弱变化时误差较大，因此本文采用模糊熵方法进行特征分析。模糊熵和样本熵一样是衡量时间序列复杂度的物理量，但模糊熵利用模糊评价中的隶属度函数代替阈值，提高了算法的统计稳定性。当转辙机出现异常时，其功率信号在某个时间尺度上的复杂度就会发生变化，显示出与正常情况下不同的模糊熵。

模糊熵的具体计算方法[17]如下：

Step1对输入的时间序列[u(1),u(2),…,u(M)]，定义相空间维数n，根据原始序列重构一组n维向量Xn(i)为

Xn(i)=[u(i),u(i+1),…,u(i+n-1)]-u0(i)

i=1,2,…,M-n+1

(5)

Step2引入模糊隶属度函数A(x)为

(6)

式中：r为相似容限度，定义为原一维时间序列标准差的k倍，即r=k·SD，SD为原数据标准差。

i,j=1,2,…,M-n+1

(7)

|u(j+p-1)-u0(j)|]

(8)

Step4对每一维向量i，取平均值可得

(9)

定义

(10)

Step5模式维数加1，对1组n+1维向量重复Step1～Step4，可得

(11)

Step6原时间序列模糊熵FuzzyEn(n,r)为

FuzzyEn(n,r)=lnΦn(r)-lnΦn+1(r)

(12)

2 混合特征选择

2.1 归一化和平滑

由于每个特征的量纲不同，因此必须对特征进行归一化。本文选择的归一化公式为

(13)

由于传感器自身精度与工作环境的影响，原始数据中往往存在大量噪声，这些噪声在特征曲线上表现为局部小波动，很有可能影响表示退化过程的趋势，因此需要使用消除噪声的曲线平滑技术。本文采用LOESS[18]来平滑选取的6个时域特征曲线和每个IMF分量的模糊熵。LOESS不仅能够消除噪声，而且能够捕获特征的重要趋势。局部加权回归平滑后曲线中的每个值都是由其前后某一段的值共同决定的，这段数据中的每个值都有其特定的权重ωi，计算式为

(14)

式中：x为需要预测的特征点；xi为以特征点为中心的某一闭区间内的其他点；d(x)为该区域的半径。

对区域内的点进行加权线性回归，即利用加权最小二乘法找到附近的点与拟合直线的误差J(θ0,θ1,…,θn)最小时θ0～θn的值，计算式为

(15)

2.2 特征选择

提取特征的质量对转辙机状态的评估有着巨大的影响，选择能够表征转辙机退化状态的特征在减少数据维度、剔除无关数据、提高预测精度等方面有着重要的意义。一个好的特征要与退化过程单调相关，且具有更好的抗干扰能力。基于以上特性，本文选用单调性、相关性和鲁棒性作为评价特征[19]。

(1)单调性度量一个特征的单调递增或单调递减的趋势，一个良好的预测特征应该与退化过程单调相关，计算式为

(16)

(2)相关性表示特征与时间的相关关系，即特征如何随时间而变化。线性曲线与时间有很强的相关性，而非线性曲线会随着非线性的增加而降低其与时间的相关性，具体计算式为

(17)

式中：Corri为第i个特征的相关性；N为样本个数；fn为第i个特征的第n个特征点；tn为时间序列。

(3)鲁棒性反映特征面对外部扰动和内部精度等干扰时，仍能保持原有趋势的能力。把特征分解为趋势分量和剩余误差分量后，利用剩余误差分量评估特征的鲁棒性。

(18)

(19)

为了选择能够表示转辙机退化趋势的最优特征，利用上述3个内在属性构造综合指标CI，然后根据CI值的大小按照从高到低的顺序进行排列。

CIi=Moni+Corri+Robi

(20)

3 基于GRU的健康状态评估

3.1 GRU循环神经网络

由于每个特征都不能完整地描述转辙机的退化趋势，所以需要将选择的最优特征进行融合，构造一个综合健康指数HI，用以更好地描述故障进程。循环神经网络是一种用来处理时间序列的神经网络模型，能够获得时间序列中的时序变化规律，而转辙机在退化过程中功率信号存在时序关系。为了使模型能够更好地体现特征的长短时序依赖关系而不造成梯度消失等问题，本文采用GRU[20]作为转辙机的状态评估模型。

图1 GRU内部结构

rt=σ(Wrxxt+Wrhht-1+br)

(21)

zt=σ(Wzxxt+Wzhht-1+bz)

(22)

(23)

(24)

式中：Wrx、Wrh为xt、ht-1对应重置门权重矩阵；Wzx、Wzh为xt、ht-1对应更新门权重矩阵；Whx、Whh为候选隐藏状态权重矩阵；br、bz、bh为偏差参数；⊙为矩阵元素依次相乘。

3.2 健康指数构建

将表示转辙机健康指数的标签和筛选后的功率特征子集作为GRU预测模型的输入数据，转辙机健康指数的预测值作为输出。其中，标签被定义为该转辙机退化的百分率，如一个转辙机在转换500次后损坏，现在时刻工作的次数为200次，则此刻健康指数为0.4[21]。HI可以表示为

(25)

转辙机健康指数的构建分为训练过程和测试过程。在训练过程中，引入Nadam梯度优化算法和均方误差(MSE)损失函数对预测值进行修正。Nadam算法与其他的梯度下降算法(如Adam、RMSProp、AdaDelta等)不同，它不仅利用梯度的一阶矩估计和二阶矩估计动态地更新不同参数的学习率，而且将一阶动量的累积加入到了梯度的更新中。Nadam算法在每次迭代时，学习率都只能在指定范围内动态变化，更直观地影响了梯度的更新过程，能够取得比Adam等算法更好的优化效果。本文通过最小化MSE损失函数来训练模型，计算公式为

(26)

测试过程中，分别将转辙机在不同健康状态下的特征输入到已经训练完成的GRU预测模型中，得到的输出即是转辙机的健康指数，用来对转辙机的状态进行评估。完整的转辙机健康状态评估模型的预测流程见图2。

图2 GRU状态评估流程

4 实验论证

4.1 实验数据

以中国铁路广州局集团有限公司集中检测系统中采集的某S700K转辙机具有退化趋势的功率曲线作为原始样本。 该转辙机从正常状态逐步转变为故障状态的整个生命周期见图3，其中75%的数据用来制作训练集，剩余25%的数据用来制作测试集。故障严重程度：0为正常；1为故障。由图3中可以看出，随着转辙机性能的退化，功率曲线的幅值也会逐渐变化，显示出与正常状态不同的趋势。因此功率曲线可以很好地描述转辙机的健康状态。

图3 转辙机功率曲线

4.2 特征提取与特征选择

(1)对10个时域特征进行计算。其分别为：均方根、脉冲因子、标准差、方差、波形因子、偏度、峰值因子、均值、峰度和峰峰值。它们的CI值分别为1.858 6、1.787 1、1.739 5、1.705 2、1.654 2、1.650 7、1.631 9、1.623 3、1.597 2和0.774 2。为了与EEMD多尺度模糊熵进行对比，只选取其中6个作为时域特征子集进行展示。其中5个特征的属性较好，另外1个特征能够反映取值下限。因此选取的时域特征分别为均方根、脉冲因子、标准差、方差、波形因子和峰峰值。

(2)对功率曲线进行EEMD分解。其中，设定迭代次数M=100，高斯白噪声标准差为原始数据标准差的0.3倍。从中选取正常状态和异常状态的EEMD分解结果作为对照，见图4。由于本文样本曲线数据点长度为170，因此EEMD分解可得6个IMF分量。计算每个IMF的模糊熵，构成特征子集，FuzzyEn1～FuzzyEn6。其中，设定空间维数n=2，相似容限度r=0.2SD。将计算得到的模糊熵与表1的时域特征一起组成特征矩阵，进行LOESS平滑。在LOESS中，设定影响拟合点的区间为30%，距离拟合点越近的点权重越大，距离越远的点权重越小。原始特征曲线与平滑后特征曲线对比见图5。

图4 EEMD分解结果

图5 原始特征曲线与平滑后特征曲线对比

(3)计算特征矩阵的综合指标CI，以选择最优特征子集。各特征固有属性对比见表2,包括每个特征的单调性、相关性、鲁棒性和CI值，并对CI值进行了排序，CI值越大，说明该特征越能反映转辙机的健康状态。集合经验模态分解将原始非线性功率时间序列分解为复杂度区别明显的子序列，这些子序列的模糊熵相对于一些时域特征来说具有更好的局部特性，更适用于健康指数的预测。本文以综合指标CI值为1.80作为阈值选择最优特征子集，因此将FuzzyEn2、均方根、FuzzyEn1、FuzzyEn6四个特征作为GRU模型的输入。

表2 各特征固有属性对比

4.3 GRU模型实验结果

本文利用GRU模型对转辙机的状态进行评估。该预测模型建立在keras库的基础上，以Tensorflow为后端用python语言进行分析。实验将最优特征子集输入到深度学习神经网络模型中，通过GRU内部门结构输出预测值，计算预测值与实际值之间的误差距离，

并利用Nadam算法实时优化和更新各个门权重，使模型的训练误差最小化。本文的神经网络由3层GRU单元和1层全连接层构成，其中单一神经元的全连接层作为整个预测模型的输出层，输出结果为转辙机的健康指数HI。

为了探究GRU模型的预测结果与神经网络参数的关系，对不同网络层数与不同随机失活率Dropout的GRU模型进行平均绝对误差MAE与均方根误差RMSE分析，见图6。

图6 预测指标随网络参数变化

由图6可以得出，GRU模型在网络层数为3且Dropout为0.3时MAE与RMSE最小，达到最优预测结果。因此本文选用的GRU模型参数见表3。

由于转辙机功率曲线是由正常状态逐渐转变为故障状态，因此训练集得到的HI值随着转辙机状态的恶化而逐渐升高，见图7。

图7 训练集HI曲线

由图7得出，可以将转辙机健康状态划分为3个阶段。第1阶段是在第127个数据点之前，健康指数在一定范围内波动，表示目前转辙机正常运作。随着转动次数的增加，HI逐渐升高，到达第127个数据点后开始趋于稳定，进入第2阶段。第2阶段(第127～175个数据点)为早期故障阶段，表明转辙机已经开始退化，健康指数急剧增加。第3阶段(第176个数据点之后)为严重退化阶段，此时转辙机逐渐退化直到最后发生故障。

为了比较GRU模型生成HI的有效性以及该HI与实际转辙机健康状态的一致性，采用极限学习机、支持向量机和BP神经网络对相同条件下的数据构造HI曲线进行对比，各模型生成的HI曲线有效性见图8。同时计算训练集预测误差error。error为预测健康值HIestimated与实际健康值HIreal的差值，即error=HIreal-HIestimated。该值越接近于0说明模型的训练结果越接近转辙机真实健康状态。预测误差结果见图9。

图9 预测误差

由图8可以看出，在第1阶段时，健康因子的预测值在正常范围内波动，但是健康因子的实际值却是单调递增的。由图9可以看出，在此阶段本文提出的GRU模型在预测时会产生较大的误差，但是在第2阶段开始也就是早期故障发生之后，GRU的预测误差明显减小，最终维持在0值附近。

每条HI曲线的3个固有属性和综合指标CI见表4。由表4可以看出，每个模型的综合指数CI都比单个特征值高，说明模型的融合过程是有效的。而GRU的CI值最高，表明该模型能够比其他模型更能反映故障趋势。

表4 各模型属性值对比

本文选用平均绝对误差MAE和均方根误差RMSE作为各模型预测的评价指标对测试集的误差进行分析，同时计算各模型的阶段预测准确率，见表5。

表5 各模型总体指标评分及阶段预测准确率

在表5所示的预测指标方面，GRU模型具有最小的MAE与RMSE，说明该模型相对于其他模型的误差波动是最小的，即该模型具有更强的预测能力与鲁棒性。由于本文将转辙机健康指数划分为3个阶段，因此阶段预测准确率定义为测试集HI的预测值所对应的故障阶段是否为实际转辙机所处故障阶段的比例。在表5所示的准确率方面，GRU模型相对于其他模型具有最高的预测准确率，说明该模型可以较好地预测出测试集每个阶段数据点的HI值，并能够在整体上较好地反映转辙机的实际健康状态。

5 结论

(1)时域、时频域特征能全面反映集中监测系统中转辙机功率信号的退化过程。

(2)利用模糊熵重构IMF分量，得到一组不同复杂度的信号子序列，降低了建立预测模型的计算复杂性。局部加权回归能够避免特征平滑过程中过拟合的问题，特征选择过程能够筛选出最能代表退化趋势的特征子集。

(3)利用GRU具有的独特门结构以及处理时间序列的特性，构建3层深度GRU神经网络预测模型，与SVM及其他神经网络模型进行对比，结果表明GRU提高了转辙机健康指数预测的准确性，具有一定的工程利用价值。