基于退化数据和非线性伽马过程的光伏组件现场寿命评估
刘卫东,文 根,鄢伟安,罗 吉,姜小华
(1.南昌大学 机电工程学院,江西 南昌 330031;2.南昌航空大学 航空制造工程学院,江西 南昌 330063)
0 引言
受质量成本持续改进和可再生能源政策的推动,太阳能光伏发电技术得到快速发展和应用,已成为当今世界缓解能源危机和防治环境污染的有效举措[1-2]。光伏组件(也称太阳能电池板)作为光伏发电系统的核心部件,其成本占系统总成本高达60%左右,且其现场寿命期内的维护费用以及退出使用后的处理费用也是项目投资、设计和运维决策的重要依据[3-8],理论界和工程界均认为光伏组件现场寿命应达到25年左右方有商业价值[9-10]。因此,准确预测和评估光伏组件的现场寿命,对科学指导其工程应用极为重要。
当前的理论研究和工程应用均以光伏组件输出功率为其性能退化的评价指标,以输出功率或输出功率退化率达到某一预定阈值定义其现场寿命或现场可靠度[6,11]。在光伏组件服役过程中,受所处环境日照时长、日照强度、温湿度、粉尘、风速和降水等具有随机性的性能退化因素的影响[12],使得其性能退化过程和现场寿命存在一定的差异。由于基于回归分析的退化轨迹评估方法原理简单,拟合函数模型的选择方法成熟,目前光伏组件现场寿命评估研究主要集中在从基于性能退化量概率分布模型以及近年来提出的基于性能退化随机过程两个方面,提出更为合适的评估方法。
基于性能退化量概率分布模型的评估方法是根据光伏组件输出功率退化量的具体数据及其呈现的直观特征,经过分布检验确定其概率分布模型,再将该模型应用于寿命评估。NDIAYE等[13]综述了2013年之前关于光伏组件性能退化的研究文献,将采用的性能退化模型概括为Pan模型和正态分布退化量模型两个主要类型。Pan模型[14]假定性能退化量服从指数衰减规律,模型中的待定参数则通过实验室加速试验确定。VZQUEZ等[15]将基于Pan模型的可靠性评估结果应用于分布在美国、西班牙两国3个不同具体地理位置光伏电池的保修期分析,指出地理位置的差异性对保修结论具有显著影响。SUBRAMANIYAN等[16]将Pan模型与基于统计的数据建模方法相结合,量化动态变化的环境应力影响,以预测光伏组件在其现场寿命期的退化率。正态分布退化量模型由VZQUEZ等[17]提出,其假设光伏组件输出功率相比于初始时刻的分位数服从正态分布,且分布参数均值和方差均为服役时间的线性函数。GEORGIITSIOTIA等[18]应用该模型描述分别位于英国和印度的光伏组件的性能退化过程并评估其现场寿命,进而预测其在现场寿命期内可能产出的能源。GONZLEZ等[19]将该模型的均值分布参数设为服役时间的指数函数,应用于服役时间达7个月的光伏组件的现场寿命评估。QUANSHAD等[20]研究了安装在炎热潮湿气候环境下的光伏组件在其服役初始14个月的早期性能退化问题,指出线性退化模型无法描述早期的性能退化情况。此外,余荣斌等[21]提出依据β分布来拟合光伏组件各个时刻退化量的分布。刘桂雄等[22]提出基于四参数λ分布的光伏组件加速退化试验的伪失效寿命分布估算方法。LARONDE等[23-24]提出基于二参数威布尔分布的加速退化试验方法,分别应用于评价处于随机温度和随机辐照度、随机温度和随机相对湿度两种环境条件下的光伏组件的现场寿命。基于性能退化量概率分布的评估方法简单直观,且能满足一定的评估精度要求。但退化量概率分布模型及其参数需要通过拟合回归分析方法确定,其准确性不仅与数据量有关,还受不同监测时刻各组性能退化数据分布特征差异性的影响。此外,退化量概率分布模型没有反映两个不同时刻退化量之间的相关性,从而给后续的现场寿命评估造成一定的偏差。为此,有学者提出综合考虑退化过程具有的非线性、随机性和动态性特征,基于随机退化过程模型的评估方法。如CHARKI等[25]采用维纳过程描述光伏组件的性能退化过程,并与Pan模型相结合构建加速试验退化模型,应用于光伏组件的可靠性评估。而根据现场性能退化数据,基于退化随机过程的现场寿命评估,仅有PARK等[26]将Gamma过程应用于光伏组件现场寿命的评估,通过对线性和非线性确定性模型、威布尔统计分布模型和Gamma过程模型及其评估结果的比较分析,认为基于Gamma过程模型所得评估结果更适合于确定光伏组件的质保寿命。但其将光伏组件的个体退化过程进行统计平均后简化为线性退化过程,且未考虑因制造过程影响因素的变异、使用过程中维护维修质量的差异性等因素的综合作用,所导致的个体之间在性能退化过程存在的差异性,使得评估结果的准确性受到影响,且无法应用于指导制定更具针对性的维护维修策略。
为此,本文基于户外监测的光伏组件输出功率,即性能的现场退化数据,考虑其性能退化过程所具有的非线性特征,采用非线性Gamma过程描述其性能退化随机过程,进而构建光伏组件总体现场寿命的评估模型,以提升评估结果的准确性;对工程实际存在的一个或多个光伏组件的退化过程与光伏组件总体的退化过程差异较大即随机效应的情况,则通过将评估模型中参数的随机变量化来描述这一随机效应,从而表征个体退化数据与总体退化数据之间的差异性,并采用随机参数的共轭分布并用最大期望算法对参数进行求解;最后将模型应用于预测某实际场地的光伏组件的现场寿命,以验证模型的适用性和有效性。
1 基于非线性Gamma退化过程的寿命评估模型
光伏组件输出功率的性能退化是严格单调的,即其退化增量是非负的,退化过程是递增的。Gamma过程是非负的、严格单调的随机过程,具有单调平稳独立的高斯增量,故可以很好地描述光伏组件的退化规律,其具体定义如下:
设{y(t);t≥0}是一个满足形状参数μ>0,尺度参数λ>0的Gamma过程,具有以下性质:
(1)y(0)=0;
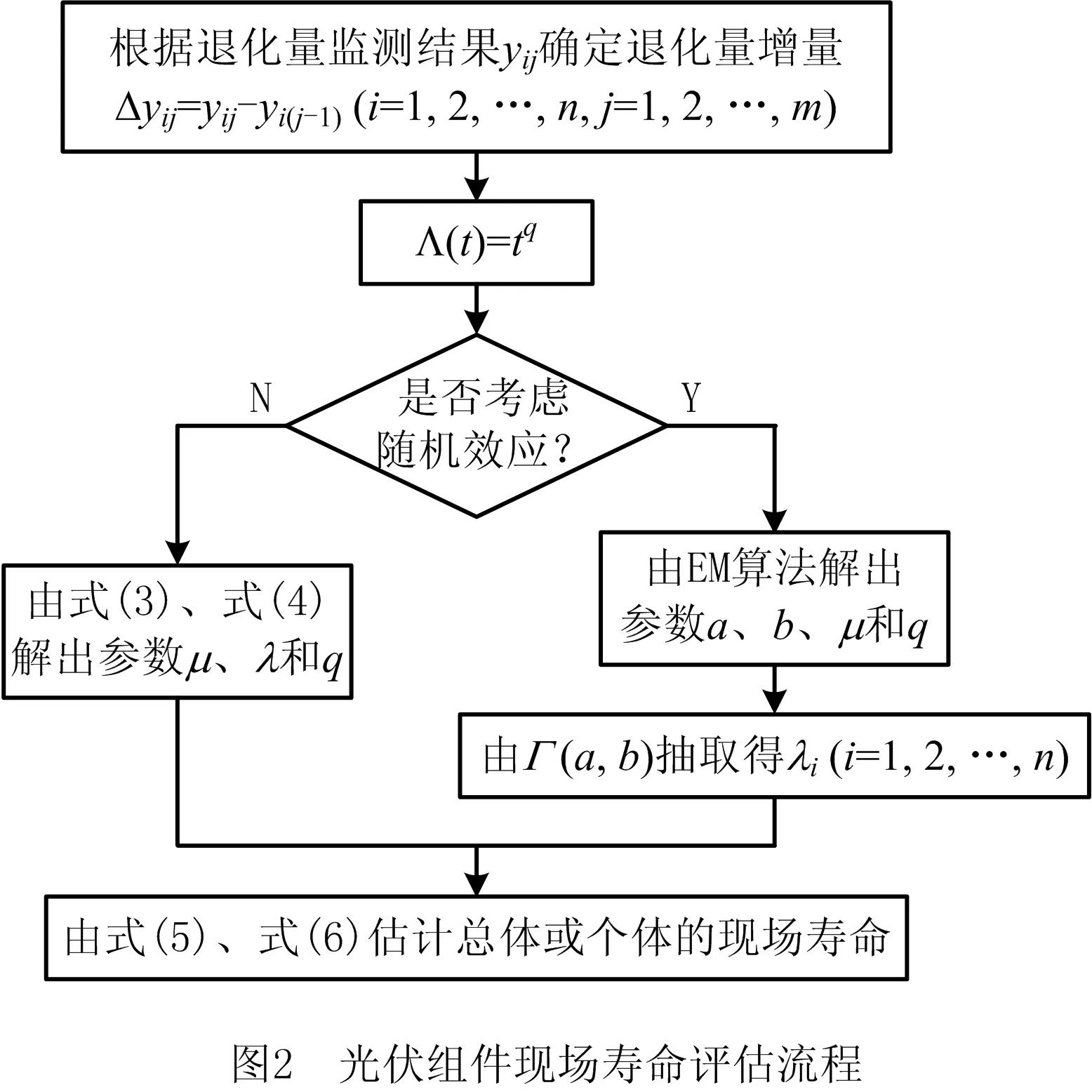
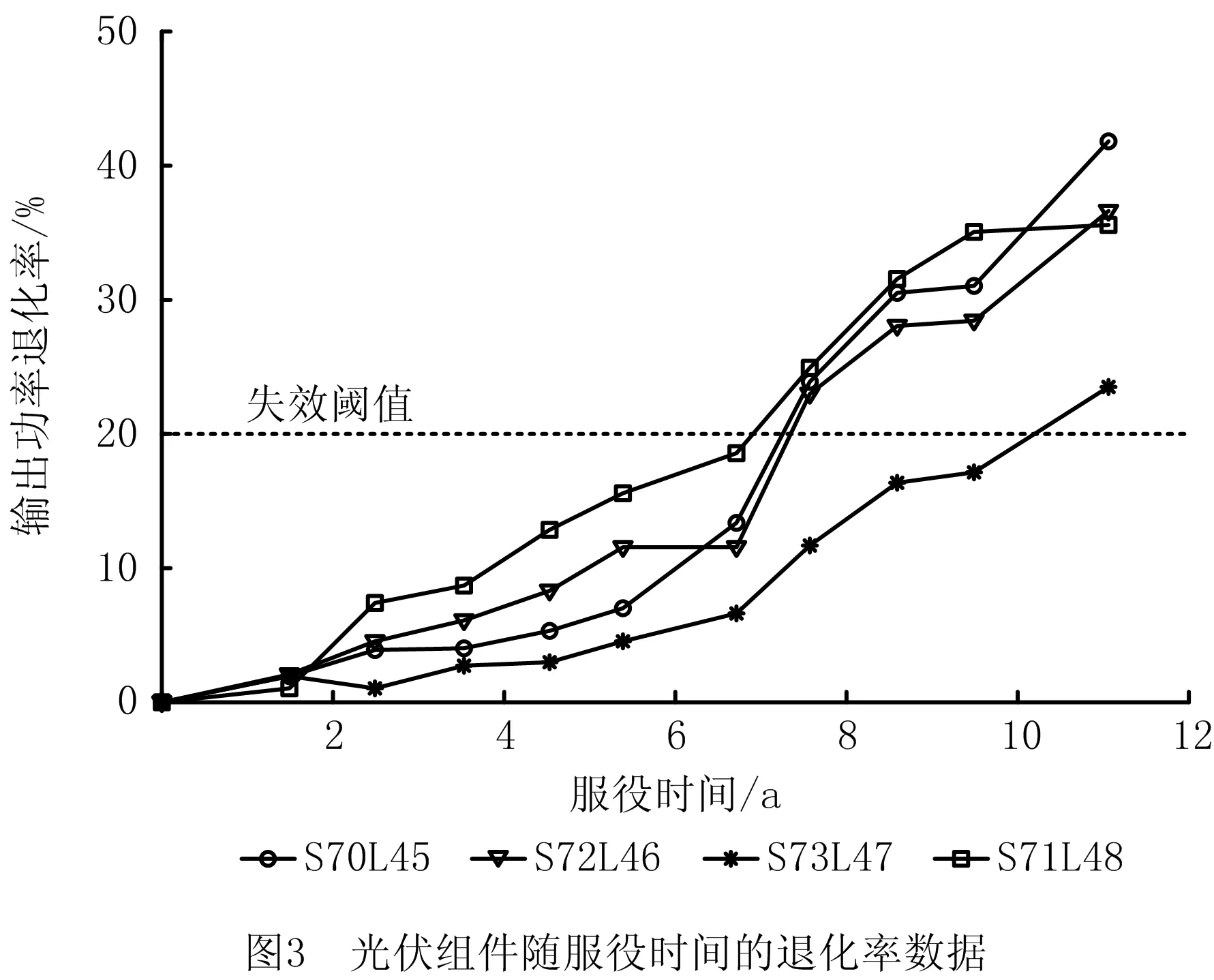
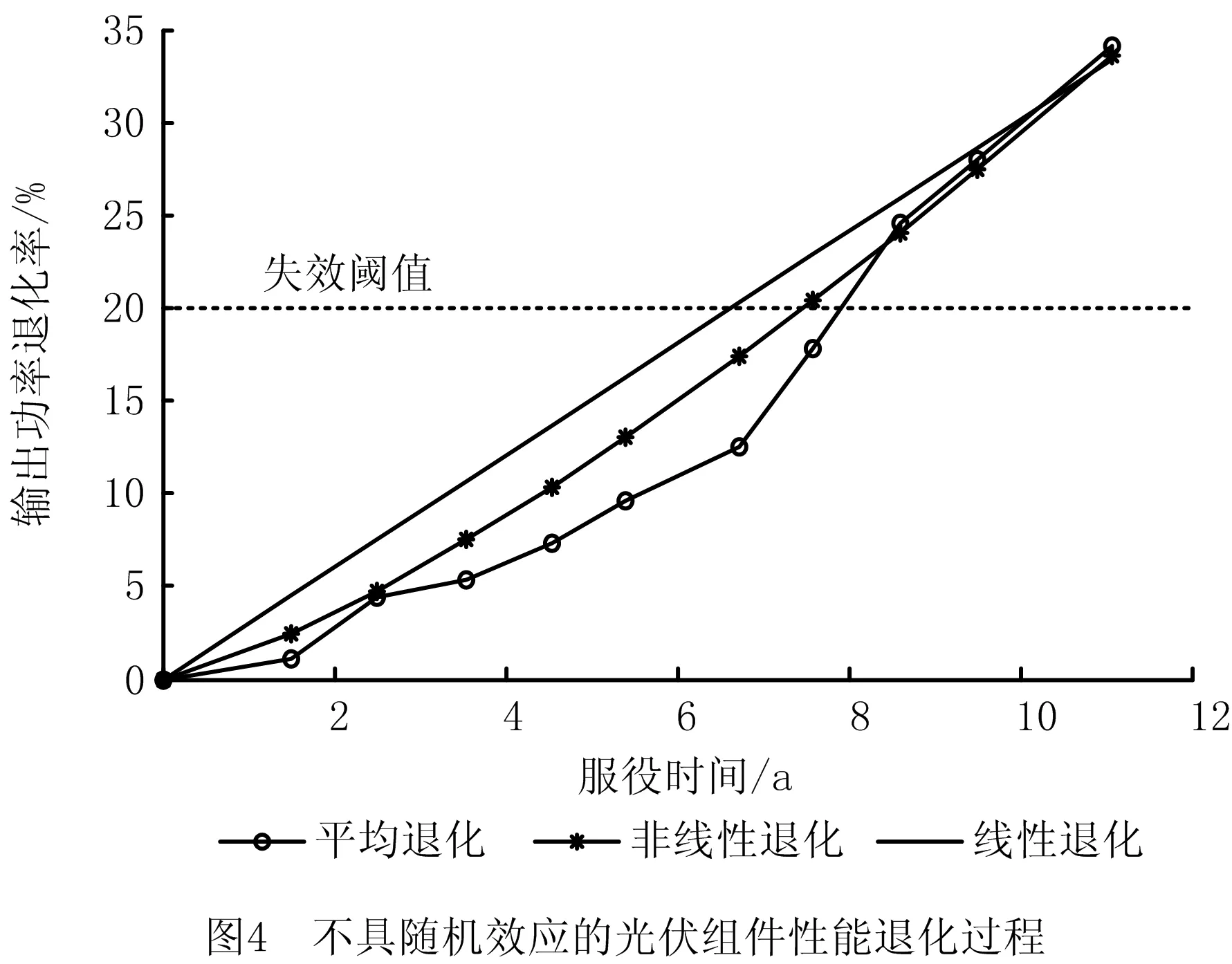
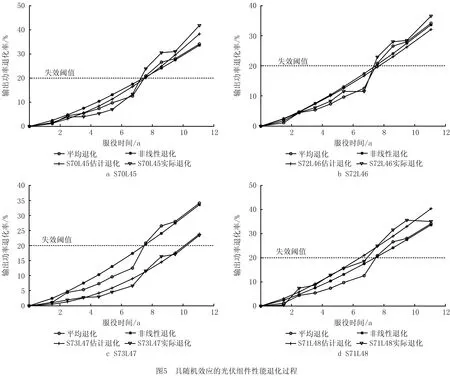
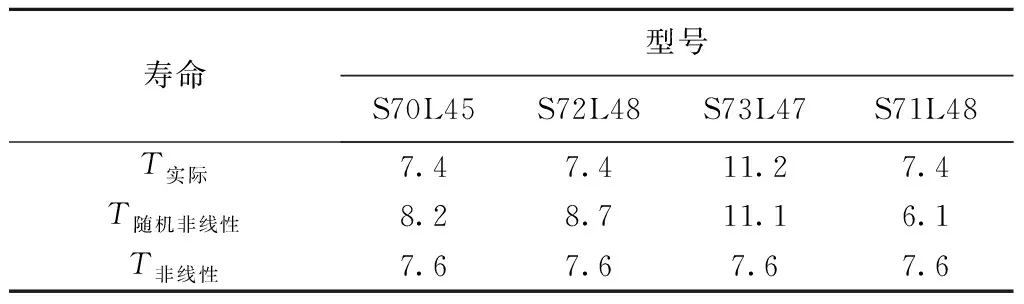
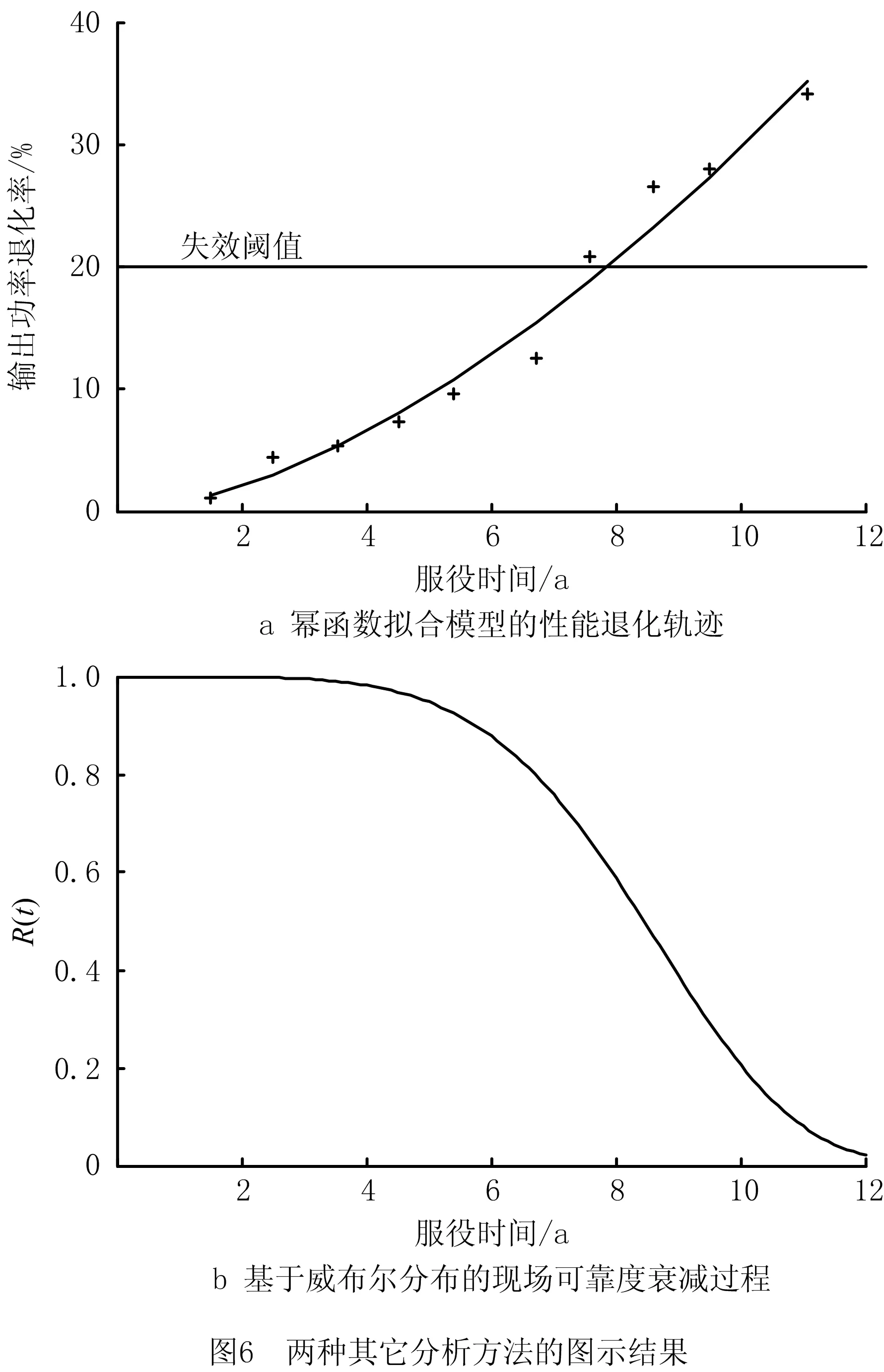
(2)y(t)具有独立的增量,即对于任意的0 (3)独立增量Δy(t)=y(t+Δt)-y(t)服从Δy(t)~Ga(μΛ(t),λ),Ga(·,·)表示Gamma分布,Λ(t)=tq为时间函数,当q=1,则为线性退化过程,且Λ(0)=0。 其中,Ga(x|μ,λ)是参数μ>0、λ>0的Gamma分布,其概率密度函数为: (1) 式中 为Gamma函数,且 假设对n个光伏组件进行性能退化试验,在时刻t1、t2、…、tm对其性能退化量进行测量并记录,其测量值为{yij,i=1,2,…,n,j=1,2,…,m},其中yij表示第i个光伏组件在第j次测量得到的累计退化量。退化量的增量Δyij=yij-yi(j-1)服从Gamma分布,即 Δyij~Gamma(μΔΛ(tij),λ)。 (2) 由式(1)可知Gamma过程含有μ、λ和q共3个未知参数,一般采用矩估计法或极大似然法[27-28]对其进行估计。考虑到在样本量较少的情况下,极大似然法的估计精度优于矩估计法,故在此采用极大似然法进行参数的估计。根据式(1)和式(2)可得Δyij的概率密度函数为 由于Δyij相互独立,故参数μ、λ和q的似然函数为 (3) 上式两边取对数后分别对μ、λ和q求导,可得 (4) 式中 (5) 由式(4)和式(5)可联立解出μ、λ和q,而光伏组件在时刻t的退化量期望可通过Gamma随机过程的期望得到 (6) 如已知光伏组件的失效阈值Df,则可求出其总体现场寿命 (7) 就单一光伏组件而言,其参数μ和λ是固定不变的;而因制造过程质量和使用过程维护维修质量影响因素的差异性,光伏组件个体之间的退化过程必然存在一定的差异,即存在随机效应。对于随机效应显著的光伏组件个体,则其现场寿命的评估需要考虑随机效应的影响,可通过将参数μ和λ分别随机变量化或同时随机变量化的方式来反映随机效应的影响。在此,仅将参数λ视为服从Gamma分布的随机变量,即λ~Γ(a,b)。通过贝叶斯公式可推导得出λ的后验分布 (8) 整理上式得 对参数λ进行随机变量化处理之后,其似然函数为 (9) 式中参数向量Θ=(a,b,μ,q)。 对式(9)进行求解时,由于增加了参数a、b,使得求解的运算量剧增并导致求解困难。在此采用最大期望(Expectation-Maximization,EM)算法[29]对其进行求解,具体求解流程如图1所示。 初始参数向量Θ(0)=(a(0),b(0),μ(0),q(0))中的元素μ(0)、q(0)通过式(4)和式(5)联立解出,元素a(0)和b(0)则由下式解出 (10) 式中λi(i=1,2,…,n)为第i个光伏组件的尺度参数。 图1中E步各期望的求解公式为 (11) 上式中E(LC)分别对a、b、μ、q进行求导,可得 (12) 图1中M步为联立式(5)、式(11)和式(12),解出参数a、b、μ和q的值,且 a(k+1)=a,b(k+1)=b,μ(k+1)=μ,q(k+1)=q;Θ(k+1)=[a(k+1),b(k+1),μ(k+1),q(k+1)]。 当不满足收敛条件时,则重新进行迭代计算。当满足收敛条件时,获得最终参数向量Θ(k+1)即a、b、μ和q的最终值,λi(i=1,2,…,n)的值则由Γ(a,b)随机抽取得到,再由式(6)和式(7)即可估计考虑随机效应的光伏组件个体的现场寿命。 根据前述基于非线性Gamma退化过程寿命评估模型和含随机效应的寿命评估模型,可以建立图2所示光伏组件现场寿命的评估流程。 为便于模型或方法之间的验证比较,在此以文献[30]给出的4个光伏组件为应用研究对象,对文献给出数据进行处理后,得其从1998年~2009年共12年服役时间的输出功率退化率数据,如图3所示。 由图3可知,光伏组件输出功率的退化增量具有非负性,满足Gamma过程的定义,且其退化轨迹呈现出非线性的特征,应采用非线性Gamma过程拟合其退化量的分布。以光伏组件的输出功率为其性能退化的评价指标,以实际输出功率等于初始输出功率P0的80%为其报废阈值[6],可定义光伏组件的现场寿命或现场可靠性,光伏组件的输出功率失效阈值 Df=0.2×P0。 初始功率的退化率为0,当功率退化率达到20%时,其对应的服役时间即为光伏组件的现场寿命。 当光伏组件的非线性Gamma退化过程不具有随机效应时,联立式(4)和式(5)可求得其参数μ=0.695 8,q=1.316 2,λ=0.490 6。 据此,可以绘出其退化量随时间变化的非线性退化曲线,如图4所示。为便于比较各模型的准确性,以4个光伏组件的平均退化寿命作为光伏组件的实际寿命,即基于4个光伏组件每年输出功率退化率平均值的平均退化曲线,以及根据文献[26]给出的线性Gamma过程得到的线性退化轨迹一并在图4中给出,而基于两种退化模型评估所得的现场寿命及相对误差如表1所示。 表1 基于两种退化模型的不具随机效应的现场寿命评估结果 由图4可知,在光伏组件服役时间达到现场寿命之前,非线性退化曲线介于线性退化曲线和平均退化曲线之间,非线性模型对实际数据的拟合程度比线型模型要好。表1结果进一步表明基于非线性Gamma退化过程的寿命评估结果相对误差远小于基于线性Gamma退化过程的寿命评估结果相对误差,前者的寿命评估结果更贴近真实值。 由图3给出的各光伏组件随服役时间的退化量数据波动情况可知,各光伏组件的性能退化过程具有一定程度的差异性,即存在随机效应,其中编号为S73L47的光伏组件具有的随机效应较其他3个光伏组件更为显著。由具有随机效应的评价模型和EM算法,可求得各参数分别为a=57.8,b=175.37,q=1.21,μ=0.709。 由Γ(a,b)抽取得到λ1=0.452,λ2=0.485,λ3=0.652,λ4=0.396。 根据计算出的参数可获得各个光伏组件具有随机效应的退化轨迹,分别与其实际退化轨迹进行对比,如图5所示。3.1节分析所得的总体平均退化轨迹和非线性退化轨迹也一并呈现在图5中。 由图5可以看出,单个光伏组件具有随机效应的退化轨迹与平均退化轨迹、非线性退化轨迹存在一定差异,其中编号为S73L47的光伏组件的差异性表现的尤为明显,且与实际退化曲线较为吻合,表明考虑随机效应的非线性退化模型对其进行现场寿命评估更为合适。为进一步分析模型的适用性和有效性,将考虑随机效应的非线性模型计算所得各个光伏组件现场寿命T随机非线性与实际现场寿命T实际、不考虑随机效应非线性模型所得现场寿命T非线性进行对比,对比结果如表2所示。 表2 随机效应对现场寿命评估结果的影响 a 由表2结果可知:对于具有显著随机效应的光伏组件S73L47而言,采用具有随机效应的非线性Gamma退化过程评估模型所得评估结果11.1a和实际值11.2a基本一致,而不具随机效应的非线性Gamma退化过程评估模型所得评估结果7.6a则与实际值11.2a存在较大程度的误差;而对于随机效应并不显著的光伏组件S70L45、S72L48、S71L48而言,采用不具随机效应的非线性Gamma退化过程评估模型所得评估结果7.6a与实际值7.4a更为吻合。 为进一步比较基于非线性Gamma退化过程的评估方法与其他常用评估方法的差异性,分别给出前述研究对象基于性能退化轨迹和基于性能退化量概率分布模型的总体寿命评估结果。 基于性能退化轨迹的评估,通过分析y=a+bt、y=aebt和y=atb;即线性函数、指数函数和幂函数3种常用的退化量随服役时间变化的回归拟合模型,经计算各模型的相关系数和误差平方和,确定幂函数拟合模型 y=0.668 4t1.6479。 该模型拟合效果最优,图6a给出了该幂函数拟合模型的性能退化轨迹。将Df=0.2即y=20代入上式解得光伏组件总体的现场寿命为T退化轨迹=7.9a,此评估结果较基于非线性或线性Gamma退化过程所得评估结果7.6a、6.8a,更接近总体现场寿命的实际值8.3a。 基于性能退化量概率分布模型的评估,首先根据各个光伏组件的退化量数据,应用线性回归模型计算得到各个光伏组件的伪失效现场寿命;其次,对正态分布、指数分布和威布尔分布3种常用的分布模型,经K-S优度拟合检验,确定最佳的现场寿命分布模型为威布尔分布,其对应的现场可靠度函数为 其随服役时间的衰减规律如图6b所示。由上式可求出光伏组件总体的中位现场寿命T0.5=8.6a,较基于非线性或线性Gamma退化过程和基于性能退化轨迹的总体寿命评估结果,与4个光伏组件的平均退化寿命作为实际寿命的8.3a更为接近。 为提升光伏组件现场寿命的评估精度,本文根据光伏组件输出功率的现场退化数据具有的非线性特征,或因制造过程质量变异、使用维护过程的系统性影响因素等所导致的个别或部分光伏组件的退化数据或规律呈现出与总体光伏组件的显著差异性,分别构建基于非线性Gamma退化过程的总体现场寿命评估模型和含随机效应的个体现场寿命评估模型。通过应用案例的评估结果表明:就总体现场寿命评估结果而言,非线性Gamma退化过程比线性Gamma退化过程的评估结果更符合实际,但评估精度不如基于退化轨迹和威布尔寿命概率分布模型的评估结果;而只有具有随机效应的个体现场寿命评估模型能够有效反映个体与总体退化过程的差异性,其现场寿命的评估结果也更为精确,有助于指导制定更具针对性的维修更换策略。 需要指出的是,本文研究目的是探讨非线性Gamma过程在光伏组件,尤其是具有随机效应光伏组件的现场寿命评估的适用性和有效性,但给出的评估模型与现有其他评估模型或方法一样存在不确定性,这一不确定性不仅受到样本数据量和数据质量的影响,还受到模型参数μ和λ随机变量化的方式及具体概率分布模型选择的影响,这也是后续需要深入开展的研究工作。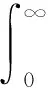

2 含随机效应的寿命评估模型
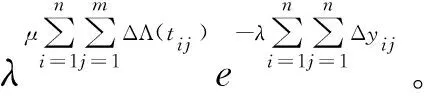

3 应用实例
3.1 不具随机退化效应的寿命评估

3.2 具有随机退化效应的寿命评估
3.3 与其他评估方法的分析比较
4 结束语

