电力系统故障下行波提取仿真实验方法设计

孙晓明， 秦 亮

（1.重庆水利电力职业技术学院电力工程学院，重庆402160；2.武汉大学电气工程学院，武汉430072）

0 引 言

传统继电保护装置的保护判据主要基于工频电气量［1-2］（即额定频率的三相电压/电流相量及由计算得到的有功/无功功率、阻抗和相角或经对称分量变换［3］得到的正、负、零序分量），故广泛采用“单片机/ARM微处理器+8 bit A/D”的嵌入式形式［4］，以500 Hz采样频率对三相电压/电流进行采样，再经离散傅里叶变换［5］或数字滤波［6］得到工频电气量。其优点是快速高效、通用性好。随着现代电力系统对继电保护的要求越来越高，基于工频电气量的继电保护的局限性逐渐暴露出来：工频电气量的测量易受短路点非线性过渡阻抗［7］、CT饱和［8］、PT铁磁谐振［9］、联络线低频功率振荡［10］、小电流接地系统不平衡电流［11］的影响，误动、拒动或错误选相的可能性增加，故障测距的误差也增大。

当电力系统发生短路故障时，短路点会产生分别向输电线路正、反向传输的电压/电流行波且行波仅会在短路故障过程中产生，故行波携带了丰富的可描述故障特征、故障方向和故障距离的信息［12］。较之工频电气量，行波电气量不受短路点非线性过渡阻抗和联络线低频功率振荡的影响，与CT饱和或PT铁磁谐振及小电流接地系统不平衡电流无关［13］，故精度高、可靠性好。行波的概念和物理意义十分抽象，其提取方法与传统工频电气量的提取方法差异很大，对实验教学和工程应用造成极大困难。本文从实验和应用的角度出发，基于业界广泛使用的Matlab/Simulink，设计了电力系统故障下行波提取仿真实验方法，所设计的实验步骤和程序可供应用型本科和高职院校直接用于科研和实验教学，易于学生掌握和转化为基本技能，还可用于实际工程，提高研发效率。

1 电力系统故障下行波提取的基本原理

为清晰，从单相输电线路入手分析。假设在单相等值双电源系统联络线f点发生接地短路故障，如图1（a）所示。图1（a）可等值为图1（b）中2个大小相等方向相反的故障电压源（即故障电压分量uf和-uf的叠加。由叠加原理，图1（b）的电气量又可等值为图1（c）、（d）的电气量的叠加。图1（d）相当于将正常运行时的等值双电源置0，并在f点施加反向电压源-uf，这时若考虑输电线路的分布参数，则将产生分别向输电线路两端传输的正、反向电压/电流行波（令+x方向为正方向）。再假设输电线路无损耗，则图1（d）中输电线路f点的故障电压分量-uf与故障电流分量if的关系可用偏微分方程表示为：

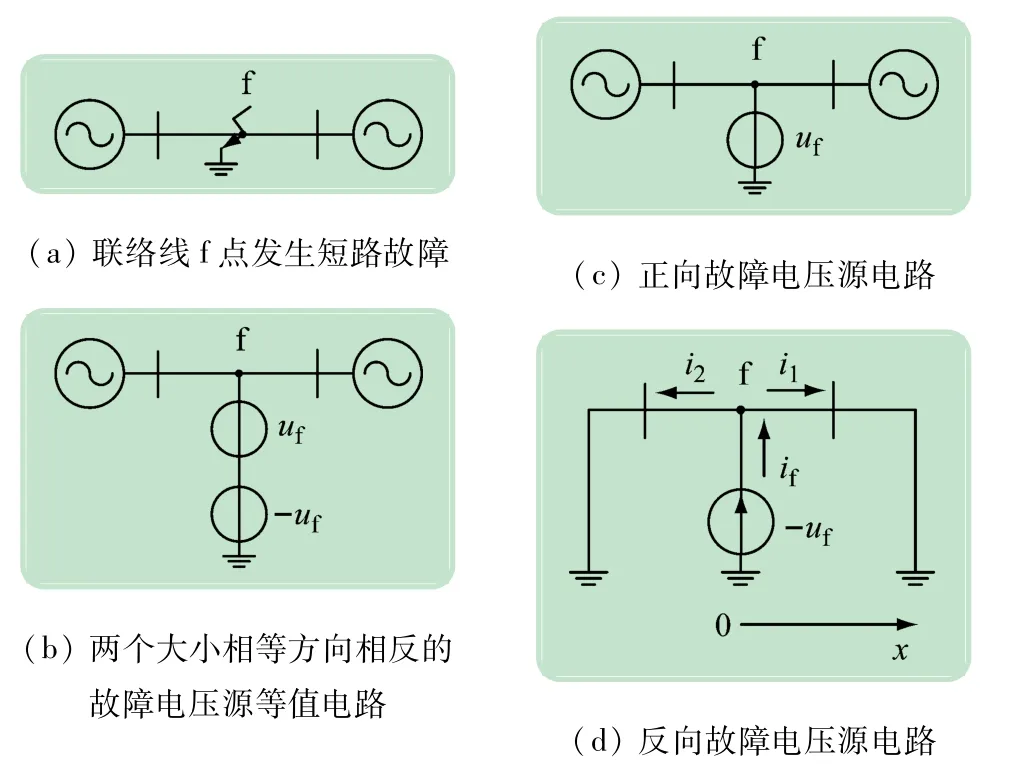
图1 行波分析用单相等值双电源系统

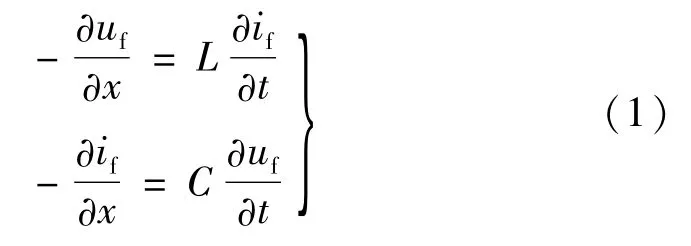
式中：x为位置变量（起始点0设在f点）；t为时间变量；L、C分别为输电线路单位长度的等值电感和等值对地电容。对式（1）两方程的两端分别对x和t再次求偏微分，经整理后可得到齐次波动方程：

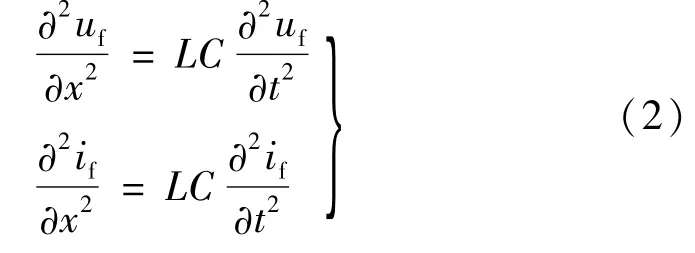
方程（2）具有D′Alembert通解：

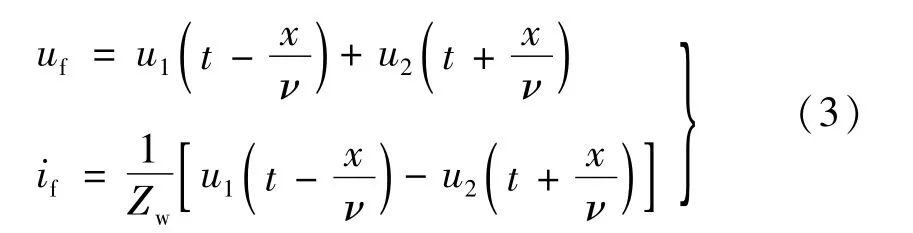
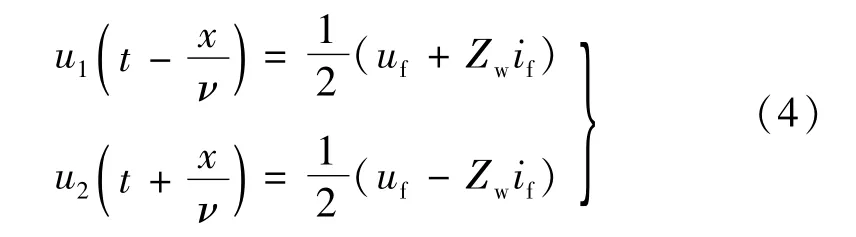
相应的正、反向行波电流为：

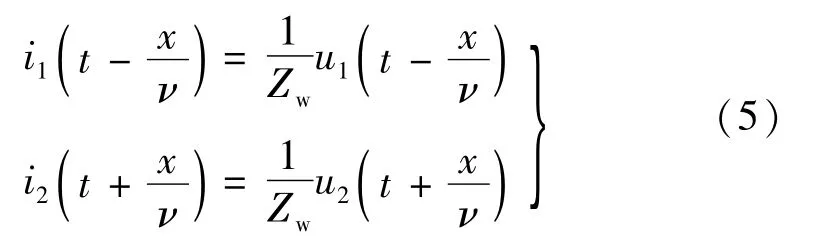
i1、i2与if的关系如图1（d）。综上，正、反向电压/电流行波可由uf、if和Zw按式（4）和（5）求得，并不需要知晓u1（t-x/v）、u2（t+x/v）、i1（t-x/v）、i2（t+x/v）的具体表达式，故式（4）、（5）是行波提取的实用公式。应指出：①若f点两侧的负载阻抗等于Zw，则正、反向电压/电流行波的反射波将不存在，但此属于极特殊的情况，实际上几乎不可能发生；②在纯金属性短路即短路电阻为0的理想状态下，f点的所有电压为0，正、反向电压/电流行波也将为0（即变为驻波，f点成为电压波节、电流波腹），出现无法检测的情况，鉴于实际中短路电阻不可能为0，仿真中未设短路电阻为0，故不会出现无法检测的情况。

注意，式（4）、（5）是由单相输电线路导出的。考虑到广泛采用的是三相输电线路，而三相电压/电流是相互耦合的，故须将其经解耦合运算，变换为相互独立的分量后才能运用式（4）、（5）。可选的解耦合运算有对称分量变换［3］、Clarke变换［14］和Karenbauer变换［15］。因3种变换大同小异，故仅以Clarke变换为例展开后续分析。设三相故障电压/电流分量分别为ufa、ufb、ufc和ifa、ifb、ifc，则其Clarke变换为：

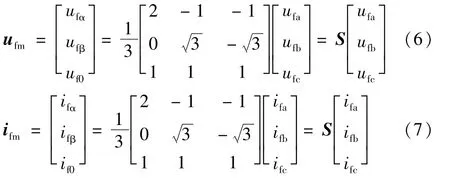
式中：ufm和ifm为故障电压/电流矩阵；ufα、ufβ、uf0和ifα、ifβ、if0为相互独立的故障电压/电流的α、β、0模分量；S为Clarke变换矩阵。将式（6）、（7）代入式（4），即可得到正、反向电压行波的α、β、0分量：

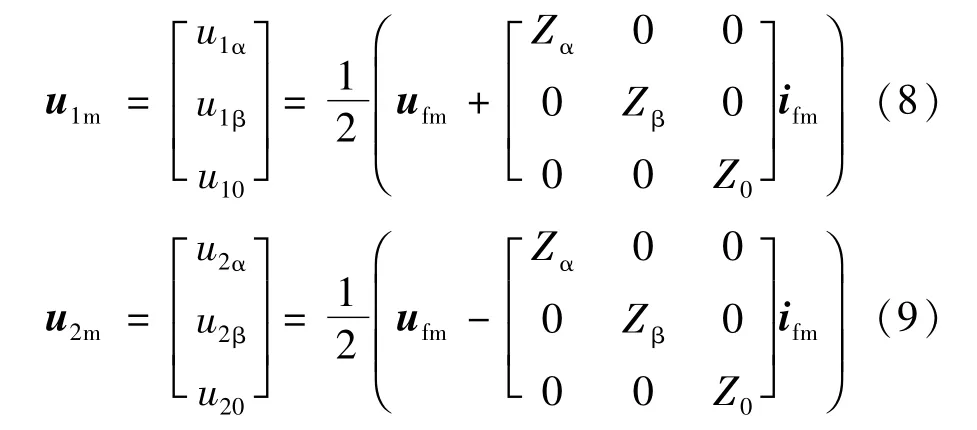
式中：u1m和u2m为正、反向电压行波的矩阵；u1α、u1β、u10和u2α、u2β、u20为正、反向电压行波的α、β、0分量，为简明略去了时间和位置变量（t-x/v）、（t+x/v）；Zα、Zβ、Z0为α、β、0模波阻抗，其与三相输电线路正、负、零序参数的关系为：

式中：L1、L0和C1、C0分别为三相输电线路单位长度的正序、零序等值电感和正序、零序等值对地电容。再将式（8）、（9）代入式（5），即得到正、反向电流行波的α、β、0分量：

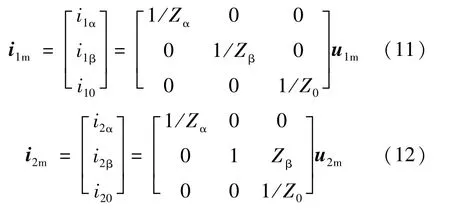
式中：i1m、i2m为正、反向电流行波的矩阵；i1α、i1β、i10和i2α、i2β、i20为正、反向电流行波的α、β、0分量，同样为简明，略去了时间和位置变量。

由式（8）、（9）还可按以下两式分别计算出电压、电流行波α、β、0模分量的反射系数（ρuα、ρuβ、ρu0和ρiα、ρiβ、ρi0）和折射系数（γuα、γuβ、γu0和γiα、γiβ、γi0），是实时或自适应行波保护的重要参数：

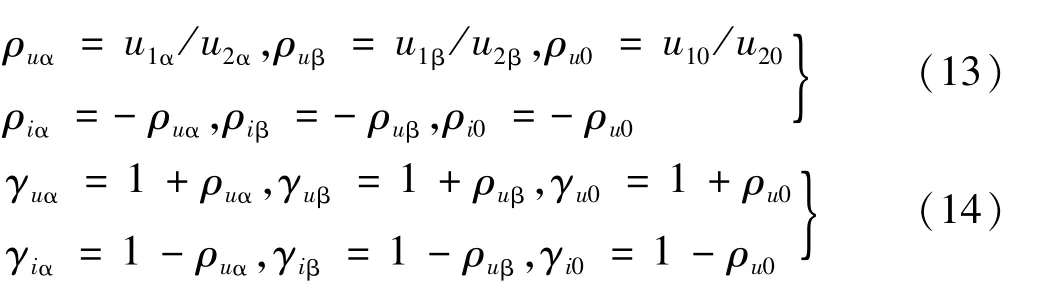
由式（6）～（9）可知，行波提取的关键在于获取三相故障电压/电流分量ufa、ufb、ufc和ifa、ifb、ifc，其基本方法是根据图1（c）、（d）所示叠加原理，用故障后的三相电压/电流减去故障前（正常状态下）的三相电压/电流。该方法简单直观，故多数文献均对此一笔带过。在实施时这些文献一般用固定时间窗截取故障后的三相电压/电流，并用同样的时间窗截取故障前的三相电压/电流，因无法准确判断故障起始时刻，故在时间窗起始时刻的选择上带有任意性，这会因基波相位差引入计算误差，造成行波信息分析的滞后性。本文对此进行了改进，用固定时间窗截取包含故障前半个周波三相电压/电流在内的三相故障电压/电流作为计算对象，既回避了判断故障起始时刻，又方便了在故障前无畸变的三相电压/电流的过零点校准相位，使计算误差最小。

2 电力系统仿真模型的建立

通过建立电力系统的SIMULINK仿真模型来产生故障前后的三相电压/电流，用于行波提取。用图2所示具有3个等值电源和4段分布参数输电线路的环形电网作为仿真案例。图中，3个等值电源均采用“Three-phase source”模型，Source1的参数设置见表1，Source2和Source3的参数“Phase angle of phase A”分别为30和60，其余参数同Source1；4段分布参数输电线路均采用“Distributed Parameters Line”模型，Line1的参数设置见表2（因实际中三相输电线路会进行空间换位以保持参数对称，故不填零序互电阻r0m、零序互电感l0m和零序互电容c0m），Line2、Line3和Line4的参数“Line length”分别为100、150和250，其余参数同Line1；三相电压-电流测量模块“Three-Phase V-I Measurement”的参数“Voltage measurement”选phaseto-ground、“Current measure-ment”选yes，其余参数用默认值，该模块将测量到的三相输电线路故障前后的电压/电流分别送到电压、电流示波器模块“Scope V”、“Scope I”进行显示，并经母线模块“Mux”合并后送至文件接口模块“To File”转换为Matlab的.mat二进制标准数据文件，以供后续处理；“To File”模块的参数设置见表3，参数“Sample time”设置为0.1 μs（即采样频率为100 kHz），这是行波采样的最低要求。

表1 Source1的参数设置

表2 Line1的参数设置

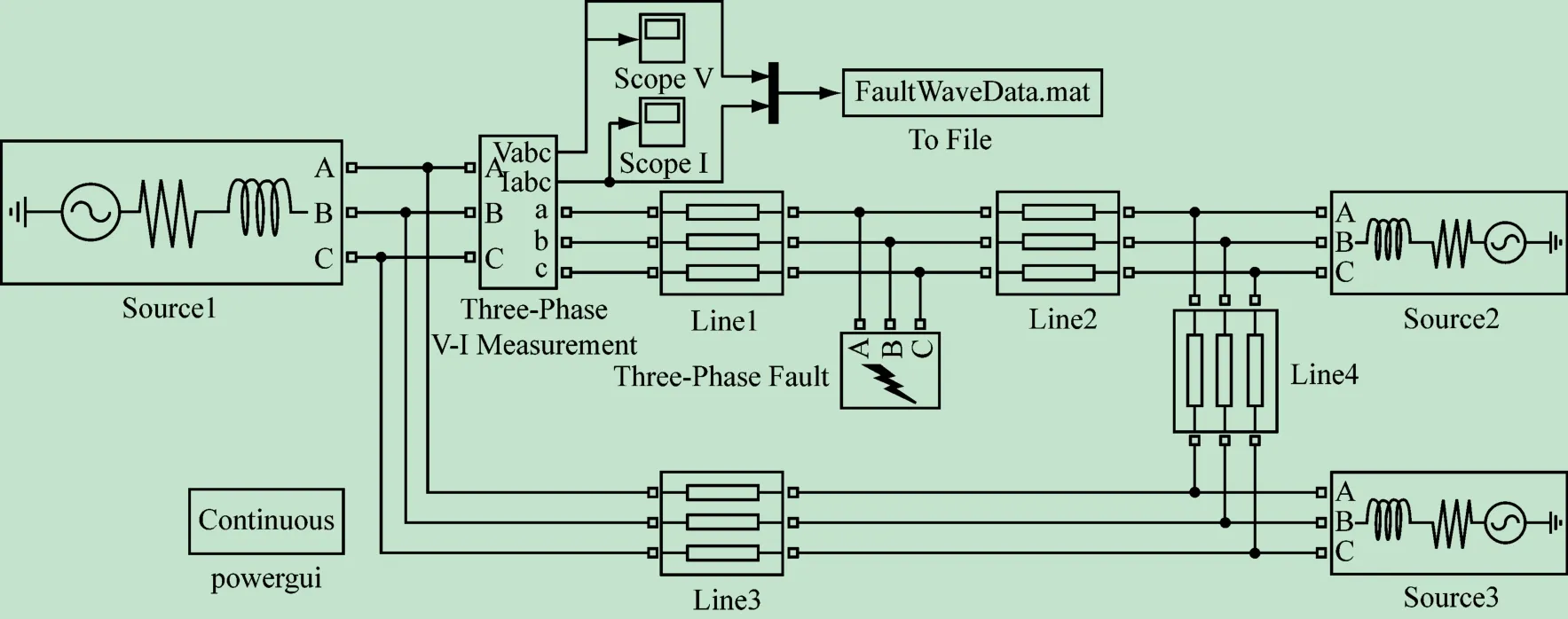
图2 用于行波提取的电力系统SIMULINK仿真实验案例

3 行波提取仿真方法的步骤和程序

利用所建立的电力系统仿真模型对输电线路的短路故障仿真后，根据表3所示的“To File”模块参数，Simulink将在工作目录下产生一个三相输电线路故障前后电压/电流的二进制标准数据文件FaultWaveData.mat。用Matlab语言编写.m程序可读取该文件中的波形数据，提取正、反向行波并计算反射系数/折射系数。按1节所述基本原理，行波提取仿真的步骤和程序如下：

表3 “To File”模块的参数设置

步骤1载入FaultWaveData.mat文件。程序为：

load FaultWaveData.mat；

用load函数将波形数据载入并以名为dat（见表3）的变量存入Workspace中。

步骤2分解dat中的电压/电流波形数据。因dat的存储格式“Save format”（见表3）选的是适宜存储非复数型数据的“Array”类型，其实质是一个矩阵：

式中：N为采样点总数；tn为采样时刻；uxn为电压采样值；ixn为电流采样值；n=1，2，…，N，x=a，b，c。式（15）说明，Simulink每次将各信号同一采样时刻的采样值写入矩阵的一列，每一列的第一个元素为采样时刻，其余元素为各信号相应的采样值。据此，分别读取dat的7行数据，即可将采样时刻与三相电压/电流的采样值分解开来。程序为：

t=dat（1，：）；

ua=dat（2，：）；ub=dat（3，：）；uc=dat（4，：）；

ia=dat（5，：）；ib=dat（6，：）；ic=dat（7，：）；

步骤3提取三相故障电压/电流分量。设故障起始时刻为tfs（如前所述tfs在现实中不能精确测定，但用本文所提改进方法，仅需判断三相电压/电流的突变量做近似估计），设所截取故障后波形的时长为Tw（时间窗），设系统额定周期为T=20 ms，则所截取故障后波形的末端时刻为tfe=tfs+Tw，故障前1个周期的正常波形的起始时刻为tns=tfs-T，故所截取的故障前正常波形的末端时刻为tne=tns+Tw。再设采样周期为Ts=0.1 μs（见表3），则所截取故障后波形始末端时刻对应的采样点序号为nfs=int（tfs/Ts）、nfe=int（tfe/Ts），所截取故障前正常波形始末端时刻对应的采样点序号为nns=int（tns/Ts）、nne=int（tne/Ts），其中int为取整函数，用于将浮点型序号转化为整型序号（程序中用round函数实现）。用所截取的故障后波形减去所截取的故障前波形，即得到三相故障电压/电流分量ufa、ufb、ufc和ifa、ifb、ifc。程序为：

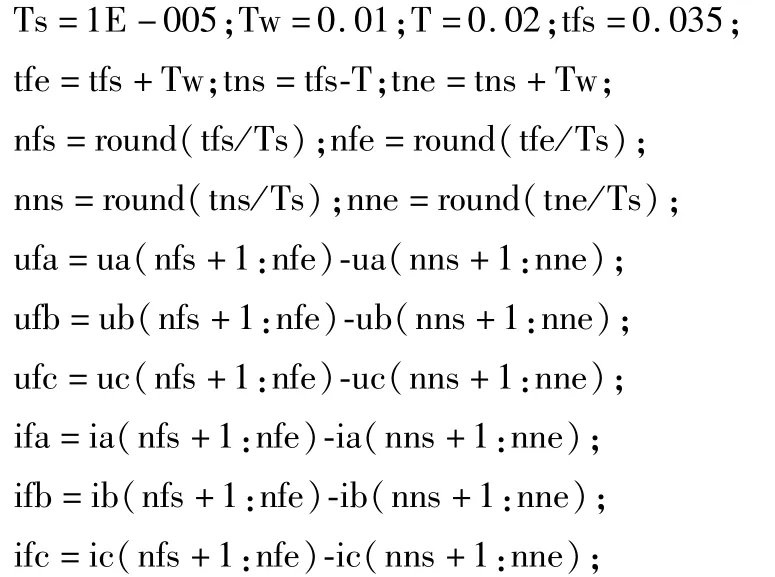
步骤4解耦合运算。采用式（6）、（7）对ufa、ufb、ufc和ifa、ifb、ifc进行Clarke变换，得到相互独立的故障电压/电流的α、β、0模分量ufα、ufβ、uf0和ifα、ifβ、if0。程序为：

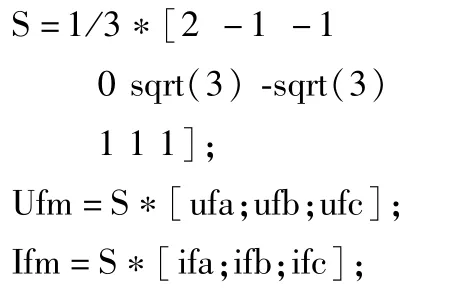
步骤5提取电压行波。采用式（8）、（9）计算正、反向电压行波的α、β、0模分量。程序为：

其中，α、β、0模波阻抗按式（10）计算，三相输电线路的正、负、零序参数见表2。

步骤6提取电流行波。采用式（11）、（12）计算正、反向电流行波的α、β、0模分量。程序为：

I1m=［1/Zalfa 0 0；0 1/Zbeta 0；0 0 1/Z0］*U1m；

i1alfa=I1m（1，：）；i1beta=I1m（2，：）；i10=I1m（3，：）；

I2m=［1/Zalfa 0 0；0 1/Zbeta 0；0 0 1/Z0］*U2m；

i2alfa=I2m（1，：）；i2beta=I2m（2，：）；i20=I2m（3，：）；

步骤7计算反射系数和折射系数。采用式（13）、（14）计算电压/电流行波α、β、0分量的反射系数（ρuα、ρuβ、ρu0，ρiα、ρiβ、ρi0）和折射系数（γuα、γuβ、γu0；γiα、γiβ、γi0）。程序为：

4 仿真结果

按表4、5设置好三相故障模块“Three-Phase Fault”的参数和标签“Simulation”的“Configuration Parameters”菜单参数。

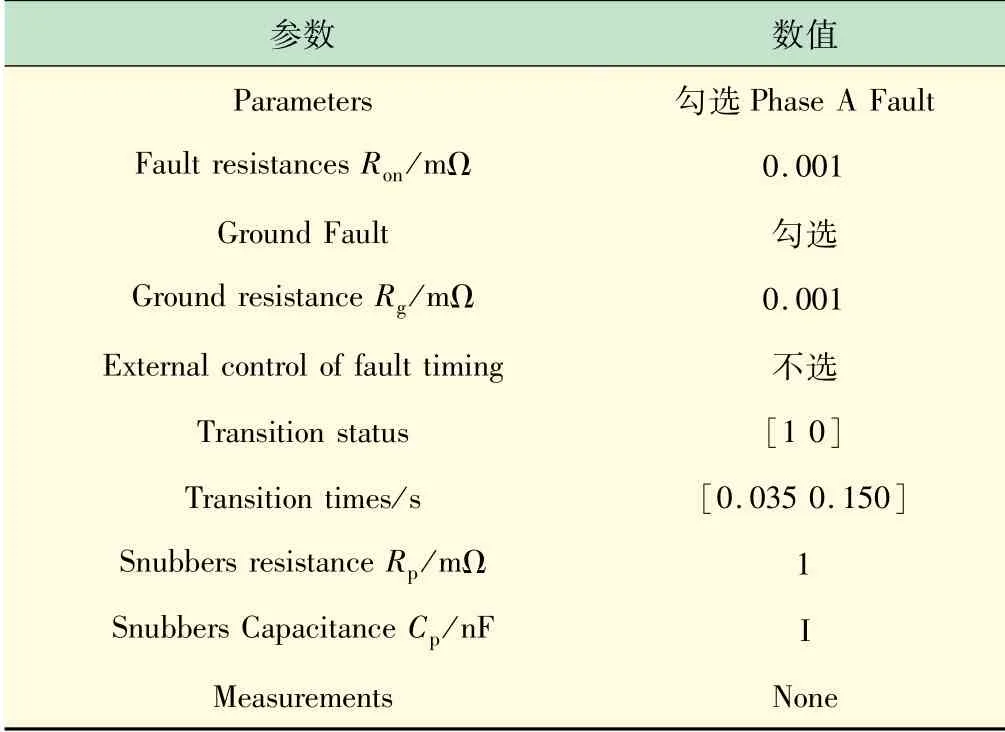
表4 三相故障模块的参数设置

表5 “Configuration Parameters”菜单的参数设置

点击“Start simulation”按钮启动仿真。仿真结束后，得到三相输电线路Line1右侧、Line2左侧A相接地故障前后的三相电压/电流波形，如图3所示。

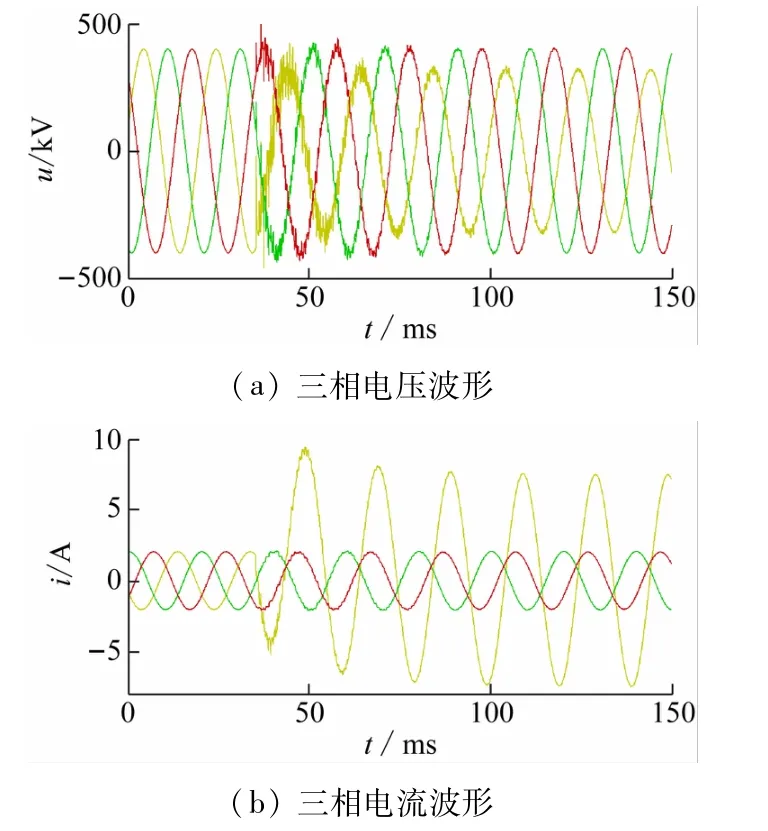
图3 A相接地故障前后的电压、电流波形（黄、绿、红—A、B、C）

执行3节所述.m程序，将提取的正、反向电压行波的α、β、0分量绘制为曲线，如图4所示。

因正、反向电流行波的α、β、0分量与电压行波的仅相差一个比例系数（波阻抗），两者波形特征相同，故不再给出图形。图4表明，正、反向行波仅是一个相对概念，经过一段时间后，两行波的方向均会发生改变，只是始终保持方向相反。再将计算出的电压行波α、β、0模分量的反射系数绘制为曲线，如图5所示。

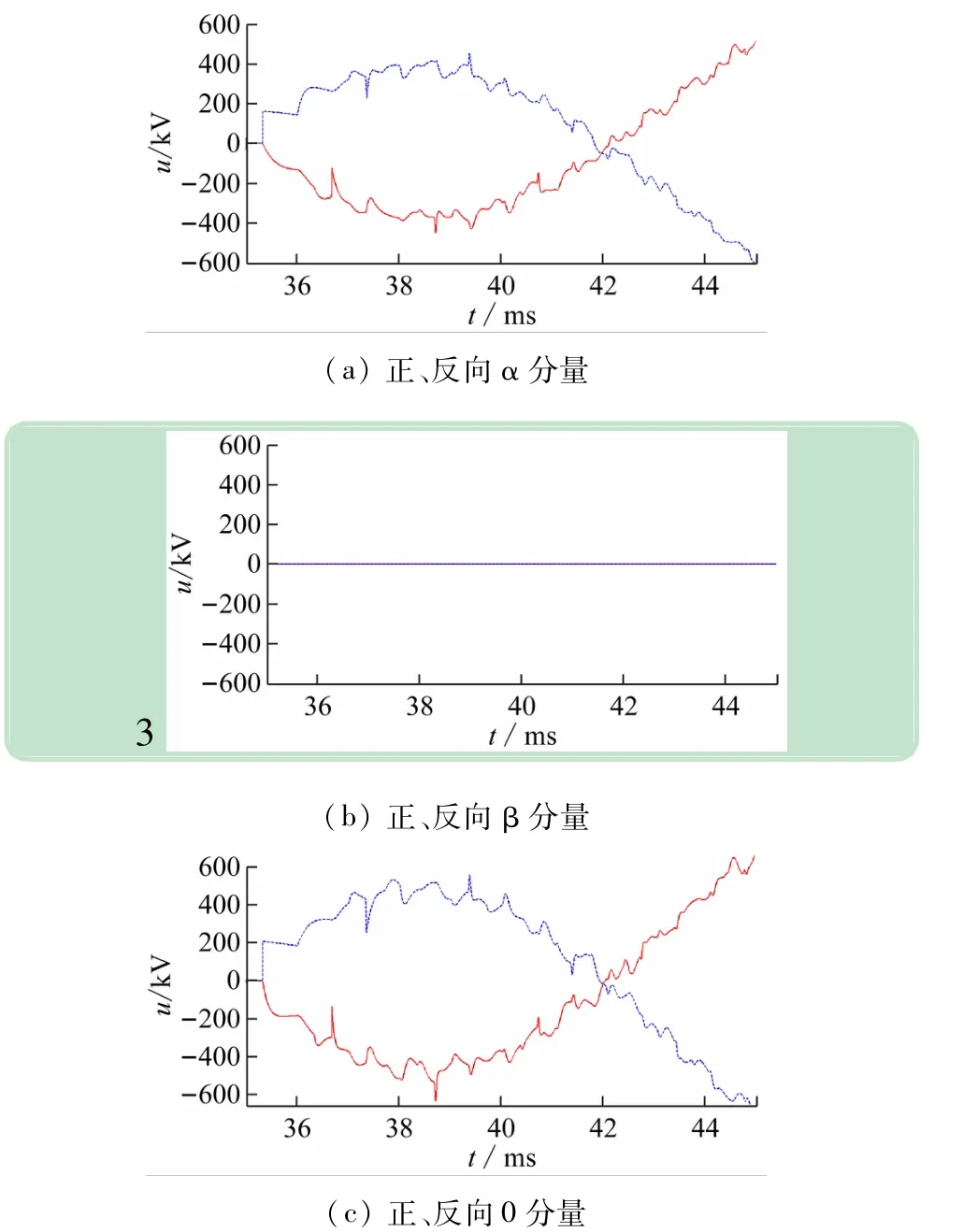
图4 A相接地故障下的电压行波分量（红、蓝、线-正、反、向）

因电压行波α、β、0分量的折射系数远大于1，其数值与反射系数很接近，故不再给出折射系数的图形。其次，因电流行波α、β、0分量的反射系数和折射系数仅与电压行波的相差一个负号，波形特征相同，故也不再给出图形。由图5可见，电压行波分量的反射系数在整个故障过程中多数时间保持相对稳定，仅在特定时刻发生突变，具有优良的故障指示功能。

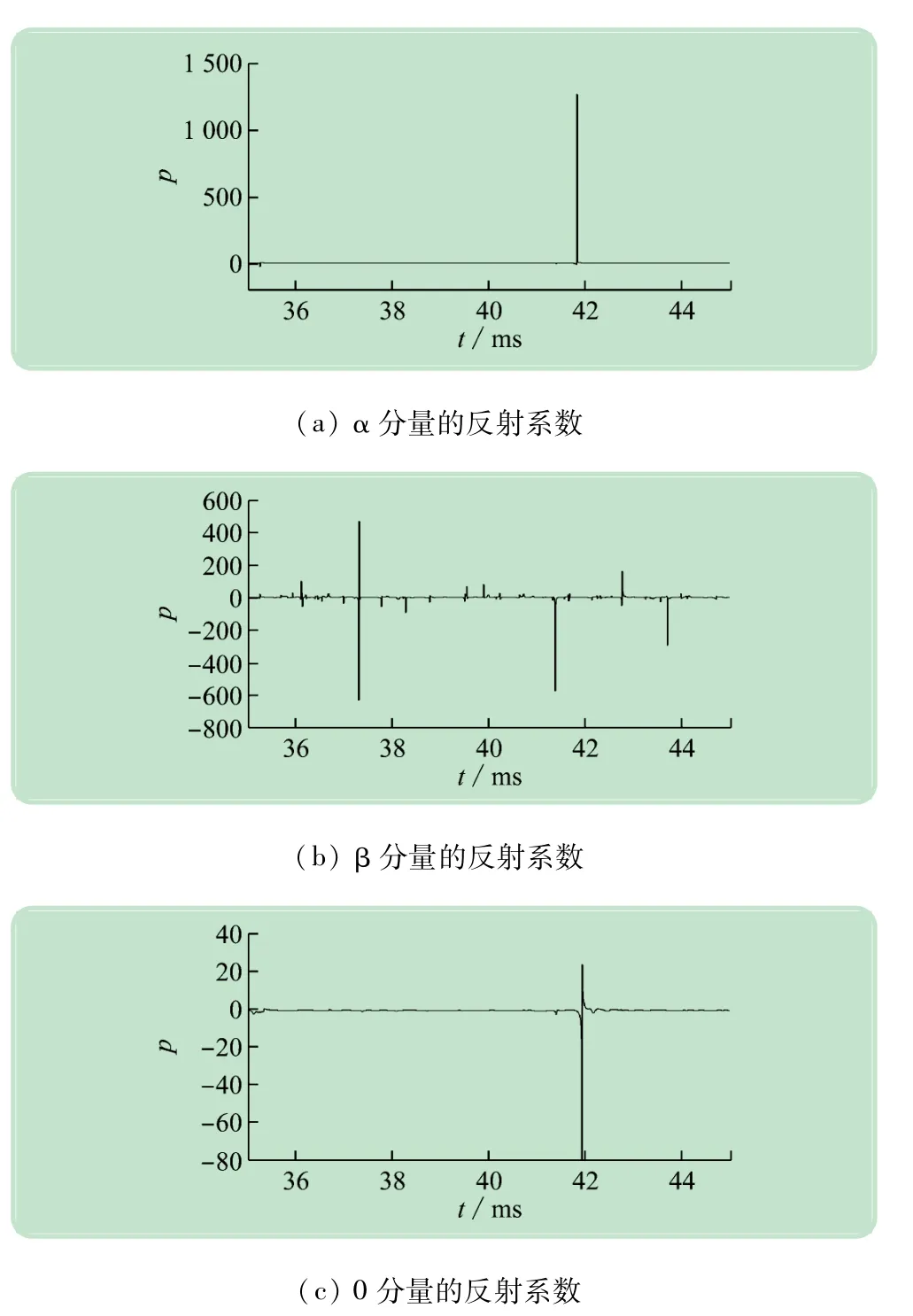
图5 A相接地故障下的电压行波分量的反射系数

为进一步显示行波的特点，再给出短路故障点不变A、B两相发生不接地短路时，正、反向电压行波α、β、0分量的曲线，如图6所示。

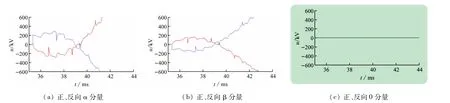
图6 A、B两相短路下的电压行波分量（红蓝线-正反向）

仿真时，仅需在三相故障模块的“Parameters”区域同时勾选“Phase A Fault”、“Phase B Fault”而不勾选“Ground Fault”，其余参数保持不变，然后依次运行仿真和.m程序即可。对比图4、6可见，不同故障类型的电压行波模分量波形不同，故可用于故障类型识别。

5 结 语

（1）所述行波提取的仿真方法，原理步骤科学严谨，程序流程简便易行，适宜教师用于科研、学生用于实验。

（2）所设计的行波提取程序可通过Matlab Coder转换为C/C++子程序，供嵌入式系统或纯软件系统的应用程序直接调用，避开复杂的矩阵变换和矩阵运算编程，提高工程技术人员的开发效率。

（3）仿真结果以直观的波形图而非抽象的理论分析，展示了正、反向行波的模分量及其反射系数/折射系数在短路故障过程中的变化特征，说明其携带着重要的故障信息，不仅可用作行波保护的判据，还可辅以模式识别算法用于故障类型识别。