基于滑模观测器的一阶系统时滞识别方法的仿真研究
强海燕, 解 思, 李万莉, 孙友刚, 董达善
(1.上海海事大学a.物流工程学院;b.离岸工程研究院,上海201306;2.同济大学a.机械与能源工程学院;b.铁道与城市轨道交通研究院,上海201804)
0 引 言
时滞现象在工程实际中普遍存在,针对时滞问题的研究层出不穷,特别是在生物学[1-2]、化学[3]、机械工程学[4]、电力学[5]等领域。时滞问题常常由于控制系统中作为反馈的执行器、传感器、局域网络、无线通信等被引入系统之中。人们为控制和设计的便利常常会直接忽略时滞,对时滞的忽略可能会降低控制系统的控制效率,甚至会致使控制系统的失稳。针对时滞系统中的时滞量识别至关重要,诸多学者对此展开了相关研究。
文献[6-9]中分别针对离散时滞问题和外部信号及控制时滞问题,设计了时滞预测算法和时滞预估辨识控制器。文献[10-11]中针对时滞参数不确定性和时滞系统线性化问题,分别提出了时滞线性化控制和系统自适应时滞辨识控制器。文献[12-16]中分别基于时滞系统不确定性、时滞预估和时滞系统抗干扰问题,分别提出了基于滑模变结构的时滞辨识自适应控制器。
综上所述,现有时滞识别方法在特定领域虽有其优势,但是在通用性、高效性方面仍然存在不足。本文针对一阶系统的时滞识别问题,建立一阶系统的离散时滞线性模型。证明所建立系统模型的可识别性,并确定系统所需的时滞识别条件。设计滑模观测器用于时滞量预测。通过典型一阶注水系统的实例进行仿真验证。
1 一阶系统的离散时滞线性模型
假设时滞模型为一阶离散时滞线性模型:
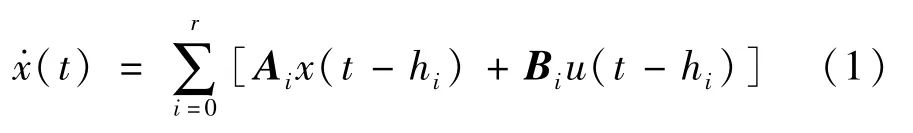
式中:0=h0<h1<…<hr≤hi为时滞量;Ai和Bi分别为适当维数的矩阵。在一般情况下,假设有两个连续的初始函数x0(t)、u0(t),并且x(t)=x0(t),u(t)=u0(t),t∈[-h,0]。
2 一阶系统的时滞可识别性
系统识别的标准方法在系统结构中已知,需要解决的问题是找到隐含在描述过程方程中的参数,即参数识别。最早的识别是针对时滞微分方程的识别,仅适用于均匀的包含无限维频谱的频谱法。本文使用的识别方法可扩展到更多通用系统,则参考模型描述如下:
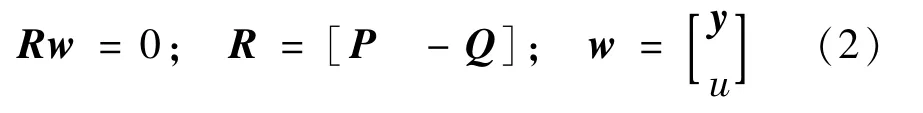
式中:P为空间上n×n的矩阵;Q为空间上n×q的矩阵。
系统的可识别性是将原始系统与式(2)进行比较,将P、Q、R、y分别由P^、Q^、R^、y^替代。式(2)表达的系统中若存在一个控制量u,使得y^=y,R^=R;即存在唯一的系数矩阵,则称式(2)表达的系统可识别。若存在一个满足条件的输入信号,则式(2)的识别性可简化为:

式中:conv R为包含R的最小闭区间,det P为卷积的行列式。
3 时滞识别条件
根据离散时滞定义及其参数可识别性定义,式(1)为离散时滞的特殊情况。则定义如下表达式:
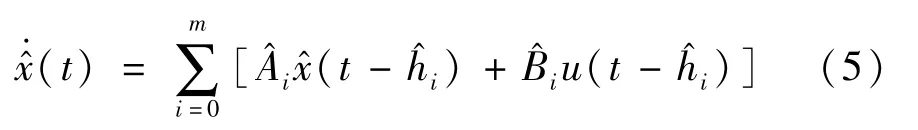
若Ai和Bi已知,则式(1)中引入H=[h1,…,hr]T,则:
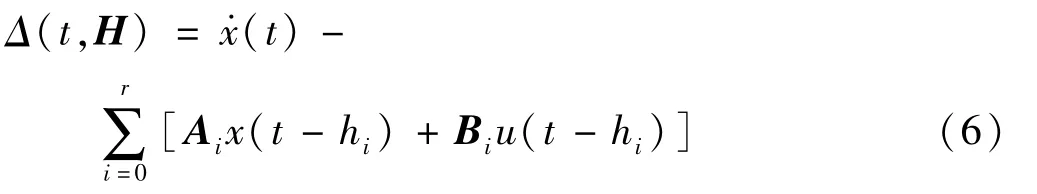
如果时滞量H不是时变的,局部可辨识性可以表示为方程解的唯一性,即通过Δ(t,H)=0求得H,对于所有t≥0。
4 观测器原理
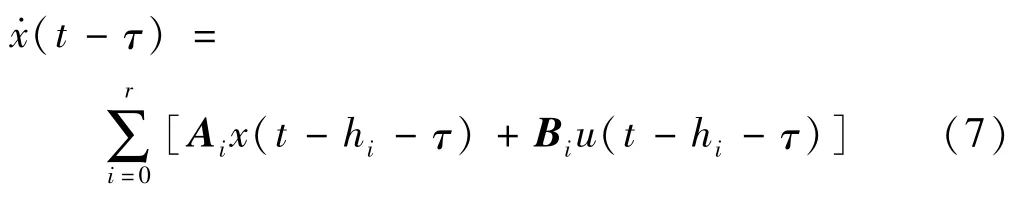
假定参数Ai和Bi已知,仅有时滞hi需要估测。接着假设已知时滞的上界h,max[h1,…,hr]≤h。
引入时滞向量H=[h1,…,hr]T,设计算法用以观测,令:

将式(9)代入式(8),并求其对时间t的一阶导数,则:
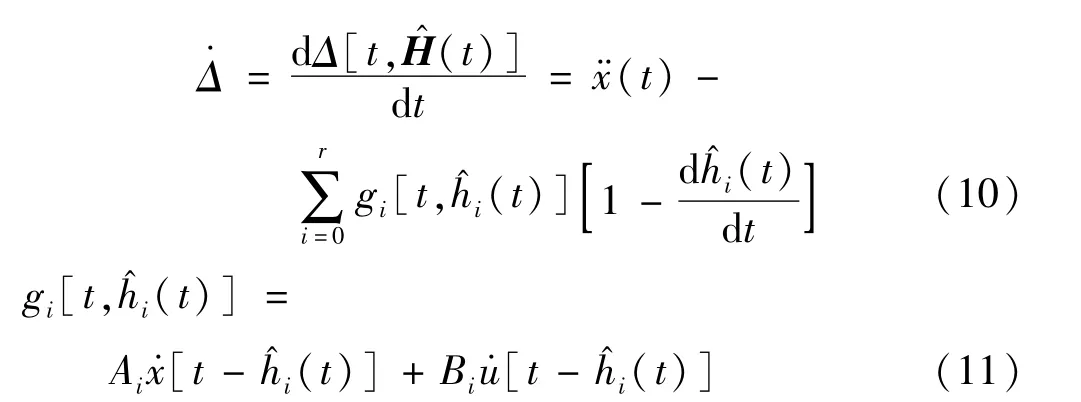
当i=1,…,r时,提出如下时滞预测器:
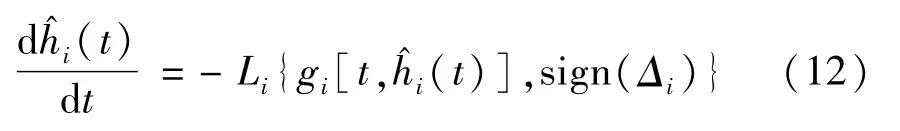
式中,sign(Δi)为符号函数,则
5 一阶系统实例仿真
5.1 仿真实例建模
根据流体力学经典一阶注水模型,建立模型并进行仿真(见图1、图2)。假设注水系统中的液体为均质、不可压缩的。图中:qin为进口处流量;R为出口流阻;he为流体液面高度;qout为出口处流量;Ae为横截面积。
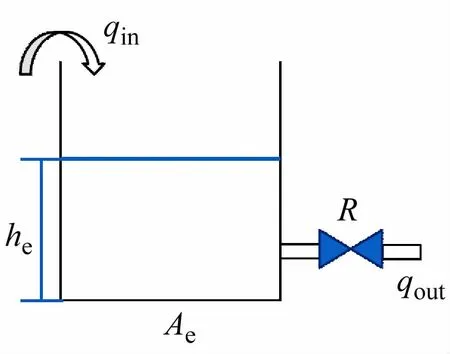
图1 注水流体系统
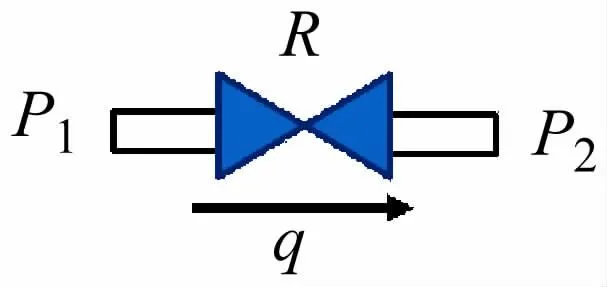
图2 流阻示意图
分别根据静压方程、绝对压强方程、表压方程和流阻方程,建立一阶注水系统控制方程:
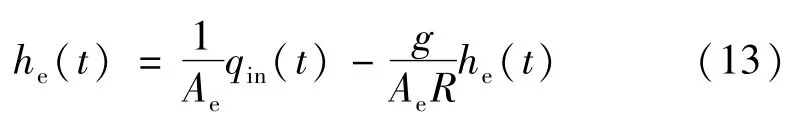
式中:Ae=1 m2;g=9.8 m/s2;R=98 Pa·s;进口处流量qin为系统输入,流体液面高度he为系统输出。
5.2 时滞识别仿真及分析
(1)一阶注水系统无输入且有未知时滞情况。其输出表达式为:
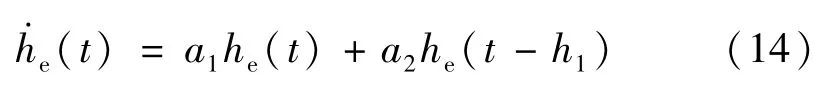
式中:a1=-0.1;a2=1;假设未知时滞量h1=1 s。
根据观测器原理可得一阶系统无输入且有未知时滞下的时滞识别仿真图,如图3所示。图3(a)~(d)分别为未知时滞预估量h^数值分别为0.8和1.2时的仿真预估曲线。如图3(a)、(c)所示,若时滞预估值与实际时滞量不匹配,则时滞辨识算法会根据规则快速调整时滞量图像的趋势并进行识别,时滞识别的图像会根据预估值和实际值向上或向下变化。由图3(c)、(d)所示,Δ根据辨识算法必须趋向于0,在1~3 s时,由于输出时滞的影响,Δ图线波动后收敛于0,则表示输出时滞量已被识别。
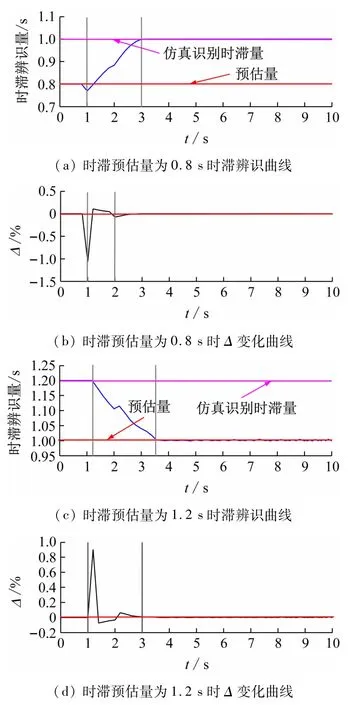
图3 无输入且有未知时滞的情况分析
(2)输入无时滞,输出含有时滞的情况。这种工况模拟在注水过程中输入无时滞,输出有时滞:
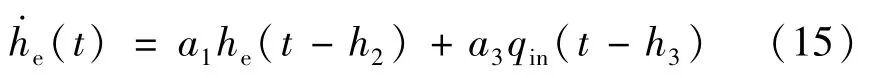
式中:a1=-0.1;a3=1。假设输出时滞量h2=2 s;输入时滞量h3=0 s。
图4所示为一阶注水系统输入无时滞而输出有2 s时滞量的仿真图。由图4(a)可见,该系统时滞量从初始时到仿真识别值,在该情况下识别算法效果较好。图4(b)表示判定函数Δ的变化,由图可知,在0~3 s的时间内,Δ有非常明显的变化趋势,而3 s以后趋于稳定,则输出时滞量被辨识出。
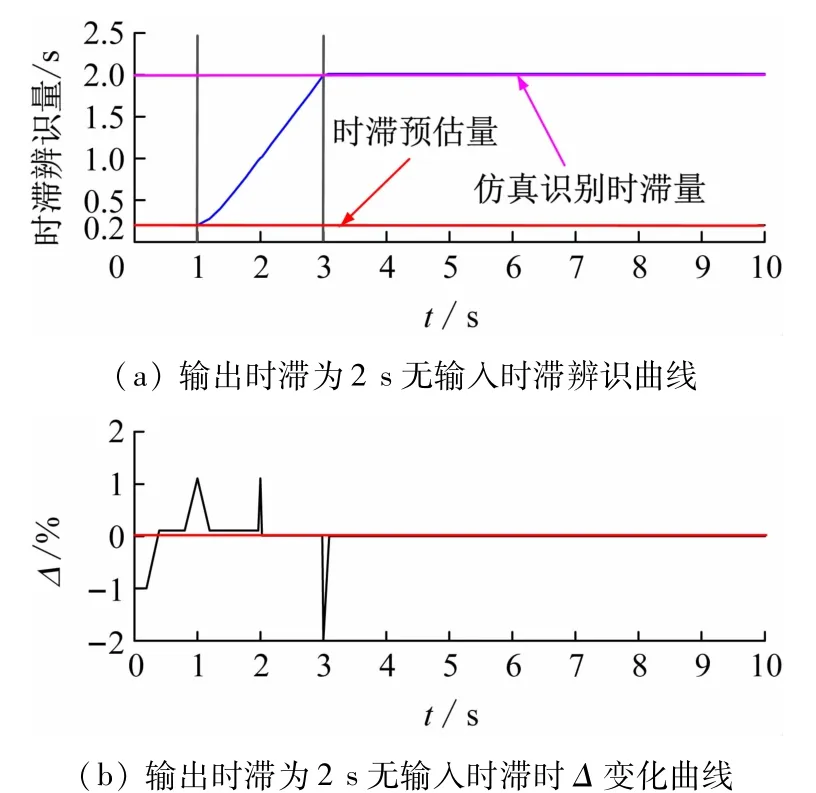
图4 输入无时滞输出有时滞的情况分析
(3)输入含有时滞,输出无时滞的情况。通过一阶注水系统输入有时滞,输出无时滞,其数学表达式如式(15),其中:a1=-0.1;a3=1。假设输出时滞量h2=0 s,输入时滞量h3=2.5 s,其表达式为:
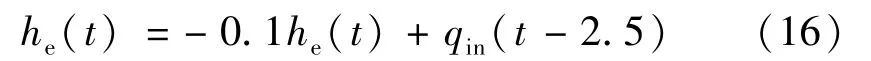
图5为一阶注水系统在输入含有2.5 s时滞量而无输出时滞的仿真图。由图5(a)易见,所识别出的输入时滞大于实际给定的时滞。图5(b)表示了判定函数Δ的变化,从图可知,在0~4 s的时间内,Δ有非常明显的变化趋势,而4 s以后趋于相对稳定,则输入时滞被辨识出。
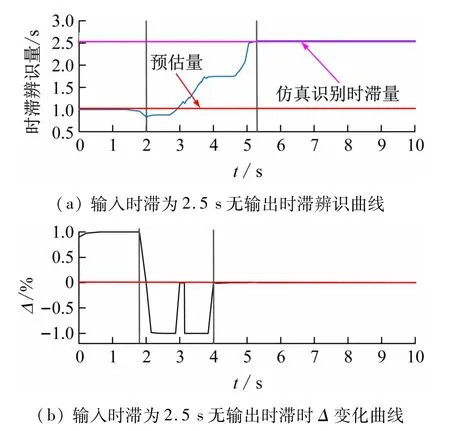
图5 输入有时滞输出无时滞的情况分析
(4)输入、输出均有时滞的情况。一阶注水系统输入输出同时有时滞的情况,其数学表达式如式(15),参数a1=-0.1;a3=1。假设输出时滞量h2=2 s,输入时滞量h3=2 s,其表达式为:
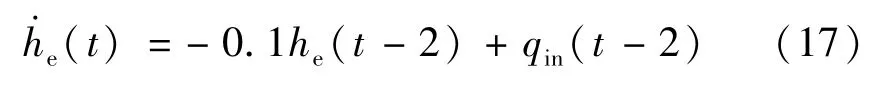
图6为一阶注水系统输入输出同时有时滞量的仿真图。由图6(a)可知,1~3 s之间仿真预测值与实际值波动较大,3 s过后,输出时滞量趋于稳定,则系统输出时滞已被识别。由图6(b)易见,所识别出的输入时滞大于实际给定的预估时滞,1~3 s之间预测值与实际值变化较大,3 s过后,输入时滞量变化趋于稳定,则系统输入时滞已被识别。图6(c)表示判定函数Δ的变化,由图可知,在0~3 s的时间内,由于预测时滞量和实际时滞量的数值变化,Δ变化趋势明显,而3 s以后趋于相对稳定,则表明时滞量已被辨识。
图6 输入、输出均有时滞的情况分析
6 结 语
本文运用变结构识别算法对时滞系统中的时滞量进行了参数预估达到识别效果。该算法将系统模型置于滑模面(用以代替未知参数或者时滞),以此替代相应的预估值。通过仿真和理论分析,本文运用的算法仍存在局限性:其时滞量必须是小时滞量才能被识别,在时滞识别过程中会出现识别出来的时滞量大于实际时滞量的情况(主要是由于预测参数Li的选择问题);时滞识别的时间较长。针对仿真和理论分析得出的结果,本文的未来工作将着重对判别预测参数Li(一阶系统主要考虑L1和L2)的最优配置问题和缩短时滞识别时间上进行展开。

