改进型并联混合有源滤波器设计研究

何克成， 温 润， 李 璐， 武学伟， 田铭兴

（1.兰州交通大学a.新能源与动力工程学院；b.自动化与电气工程学院；c.甘肃省轨道交通电气自动化工程实验室，兰州730070；2.西北民族大学电气工程学院，兰州730109；3.国网兰州供电公司，兰州730070）

0 引 言

随着电力市场开放和各种用电需求的出现，大功率二极管和晶闸管整流器、周波变流器、电弧炉等非线性负载，以及大量低功率二极管整流器、分布式电源、电动汽车等设备不断接入电网，使得谐波的产生机理和传播特性变得更加复杂，且更易引发谐振、谐波扩散以及稳定性问题［1-2］。

无源滤波器（Passive Power Filter，PPF）是常用的谐波治理装置，其结构简单、成本较低，但存在只能补偿特定次谐波、易受电网参数影响等缺点；有源电力滤波器（Active Power Filter，APF）能够准确、快速地对谐波进行跟踪补偿，但其缺点是成本过高。为实现微电网电能质量的改善和优化配置，由PPF和APF组成的并联混合有源滤波器（Shunt Hybrid Active Power Filter，SHAPF）补偿系统成为一种可行的解决方案，该系统能以较低的成本对非线性负载进行较好的补偿。面对大容量、高效率的补偿要求，SHAPF需要进一步降低成本和系统复杂度［3-5］。文献［6］中针对电流源典型负载进行SHAPF控制系统设计和仿真。文献［7］中将单周控制方法应用于SHAPF的电流控制，仿真效果良好。文献［8］中研究了一种SHAPF的复合控制策略，综合性能更优。文献［9］中针对一种SHAPF结构进行了设计和仿真分析，但对参数设计过程未作详细讨论。

为进一步降低补偿非线性负载时系统的容量和成本，改善SHAPF的补偿性能，针对两种改进的SHAPF补偿系统进行了研究，建立补偿系统等效电路，探讨系统关键参数设计方法，减小SHAPF系统有源部分的容量和体积，提出一种双闭环控制系统，能够有效提升系统稳态精度和动态性能。Malab仿真表明，该SHAPF系统均具有优良的滤波效果，综合成本低，是适用微电网电能质量治理的理想补偿系统。

1 SHAPF的工作原理及等效电路

PPF单相电路结构如图1（a）所示，可将其直接并联在谐波源两端，利用RLC元器件的谐振特性对系统中的某一特定频率形成一个低阻通道，该通道与系统阻抗形成并联分流关系，使谐波成份从滤波系统中流过。因其结构简单、运行稳定得到了广泛应用。

并联型APF基本结构和工作原理如图1（b）所示。APF实时监测负载电流iL并生成补偿电流的指令信号，由脉冲宽度调制（Pulse Width Modulation，PWM）电路控制变流器产生补偿电流ic并注入电网，减小电源电流中的谐波含量ish，使电源电流is趋于正弦。APF可以动态检测系统谐波电流并进行实时补偿，但在大容量补偿时造价也相对更高。

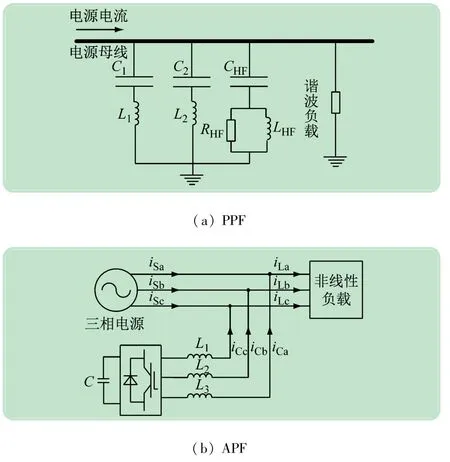
图1 PPF和APF工作原理图

单一有源元件和单一无源元件的电气连接方式有8种，如图2所示。考虑有源元件的容量、能否补偿无功、终端电压是否畸变、元件是否冗余等，SHAPF仅有3种结构是理想的，分别是图2（b）、（e）和（f），通常使用的只有后两种，故本文对图2（e）、2（f）两种结构进行研究［10-12］。

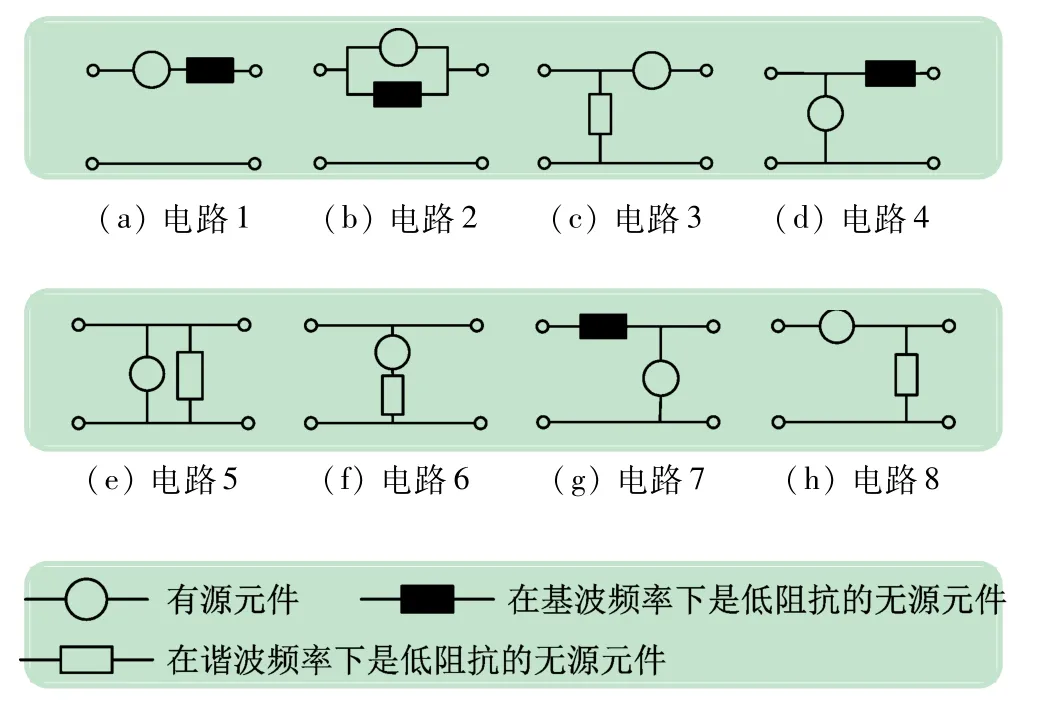
图2 单一有源和单一无源元件构成的电路结构

1.1 第1种SHAPF结构

第1种SHAPF结构如图2（e）所示，对应的单相谐波补偿等效电路如图3所示，其中iLh为负载电流中的谐波成分，ish为电源电流中的残余谐波。正常工作时，由PPF补偿谐波电流中的低频和高频部分，APF仅对中频段谐波电流进行补偿，因此有源部分容量较小。该结构适宜补偿大容量电流源型非线性负载。

由图3可得：

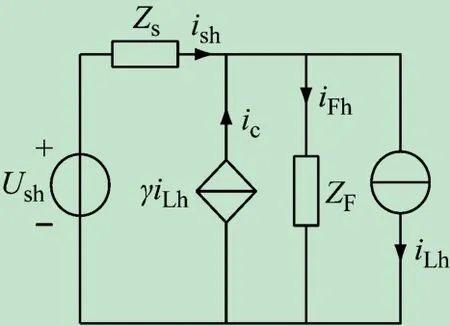
图3 第1种并联混合型APF的单相等效电路

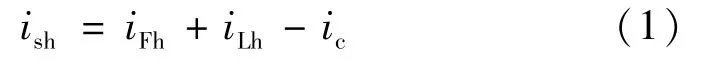
n次谐波电压：

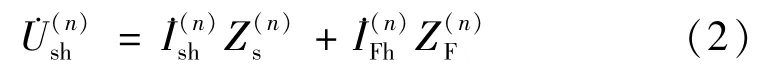
由于

由式（1）～（3）可得n次谐波电流：

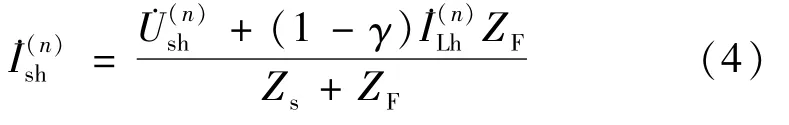
由式（4）可知，谐波电流的大小与γ的取值和PPF支路的等效谐波阻抗ZF有关。

1.2 第2种SHAPF结构

第2种SHAPF结构如图2（f）所示，对应的单相等效电路如图4所示，APF与PPF串联可有效减小滤波支路的谐波阻抗，将负载中的谐波电流引入滤波器支路，消除电源电流中的谐波含量ish。该电路结构还可避免PPF与微网系统产生谐振，且APF不承受基波电压，适用于高压系统。

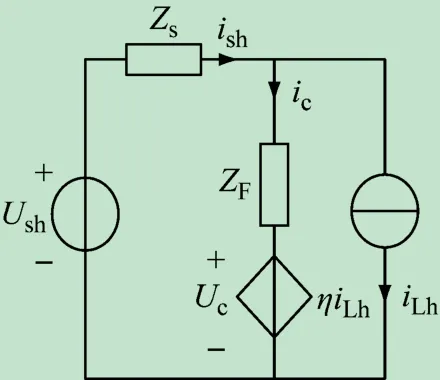
图4 第2种并联混合型APF的单相等效电路

分析图（4）可得：

n次谐波电压：

而

由式（5）～（7）可得n次谐波电流：

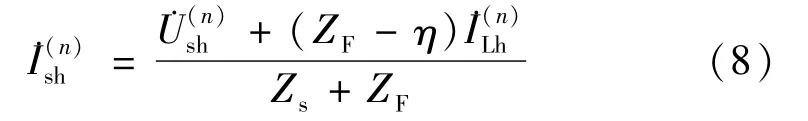
由式（8）可知，谐波电流的大小与η的取值以及PPF的谐波阻抗ZF有关。

2 主电路关键参数设计

2.1 并网耦合电感设计

并网耦合电感L对SHAPF系统的补偿效果有直接影响。若电感取值过大将直接影响SHAPF补偿电流的响应速度和输出效果，且增加系统体积和成本；取值过小将导致补偿电流变化速度过快，增加高次谐波的含有量。SHAPF功率单元在前述补偿目标下需满足［13］：

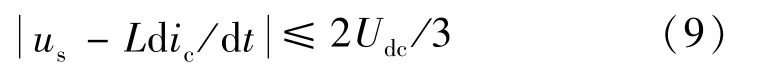
式中，Udc为SHAPF直流电压平均值，令补偿电流各次谐波幅值之和：

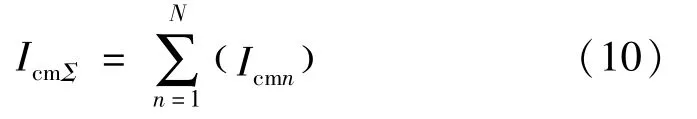
一般取电压波动率ε=ΔUmax/Udc，（0＜ε＜1）其中ΔUmax为最大纹波电压。由式（9）、（10）可得［14］：

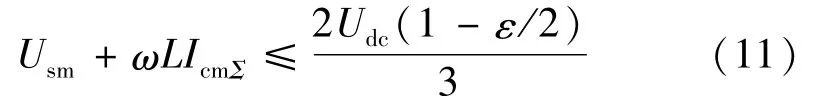
式中，Usm为电源电压峰值。由式（11）可得：

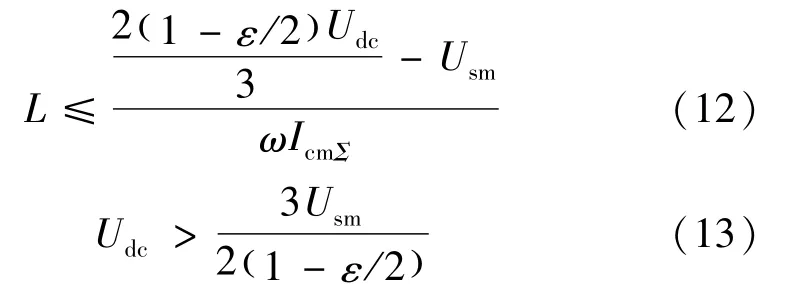
并网耦合电感需要同时考虑电流脉动幅度和开关频率。设SHAPF开关频率最大值为fsmax，对应的补偿电流脉动频率的最大值fcmax；该谐波电流的幅值为Itm，其与基波电流幅值I1m之比设为δ，相位为θc，对应的电感压降为：

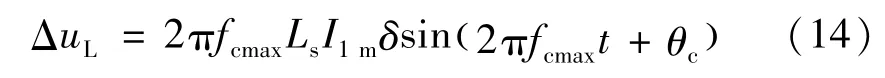
对应fcmax次谐波电流由PWM调制产生，其调制电压：

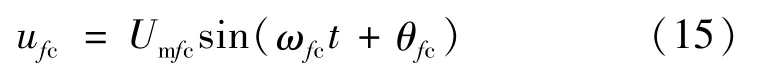
式中，调制电压幅值和相位分别为Umfc和θfc。因此Δuc与ufc的幅值及频率应相等：

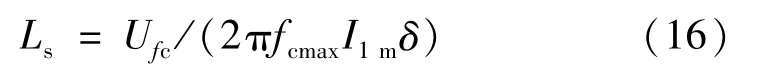
利用Fourier级数可求出Ufc=Udc/π，fcmax=3fsmax/2［13-15］。设补偿电流脉动量最大值hmax=δI1m，将以上代入式（16），结合式（12）可得：

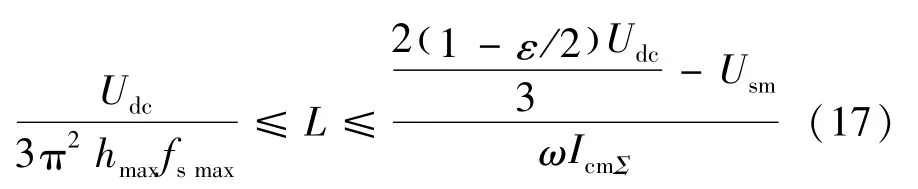
因此交流耦合电感额定值：

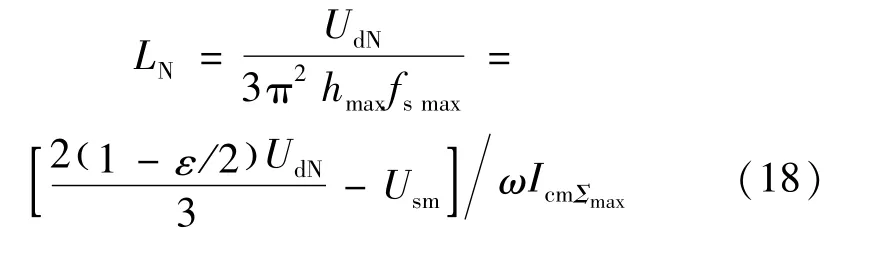
文献［16-20］中针对整流型谐波负载给出了APF电感取值的计算范围，相比而言式（18）的设计方法简单易行，不会存在无解的情况，减少了功率单元设计时的盲目性。文献［16］中给出的电感上限计算公式为：

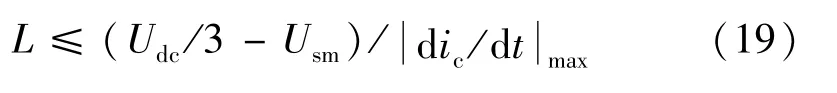
事实上，设常数Q=Udc/3（Q＞0），结合式（11）可推得式（19）。文献［16］中的算例中给出了由式（19）解得的电感值的仿真结果，其开关纹波过大，未能满足补偿要求。这说明Q=Udc/3的取值过小，本文在分析中取，所导出的式（18）取值范围更加合理。

2.2 无源滤波器设计

SHAPF中的PPF补偿谐波电流中的低频和高频部分，可使有源部分容量进一步减小。PPF的设计原则是，结合系统当前的功率因数和最终想要达到的功率因数，算出需要产生的总基波无功功率；再依据需补偿的无功功率和各滤波器支路参数间的关系计算电容和电感值；由品质因数计算出电阻值。

2.2.1 单调谐滤波器设计

需要补偿的基波无功功率为：

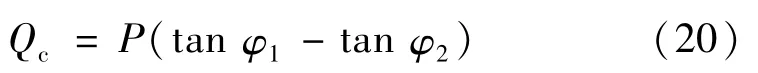
式中：φ1为当前功率因数角；φ2为目标功率因数角。根据n次谐波电流占总谐波电流的比率求取无功功率。故各PPF支路需要补偿的无功功率为：

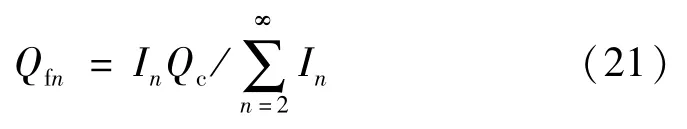
电容器的增值系数：

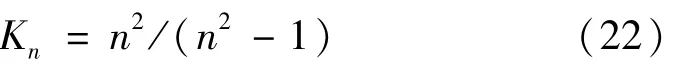
故电容值：

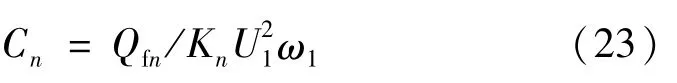
式中，Cn、Qfn分别为n次滤波器支路电容值及无功功率。故电感、电阻值分别为：

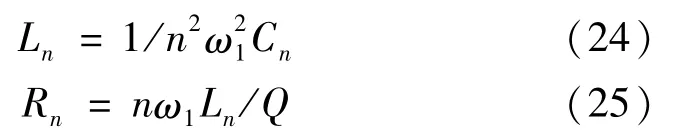
式中，Q为品质因数，本文取Q=40。

2.2.2 高通滤波器设计

高通滤波器产生的基波无功功率为：

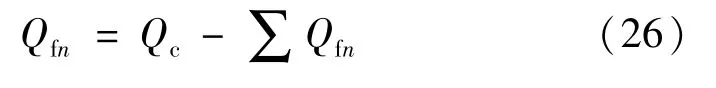
式中，∑Qfn为单调谐滤波器组产生的总基波无功功率。故电容值：

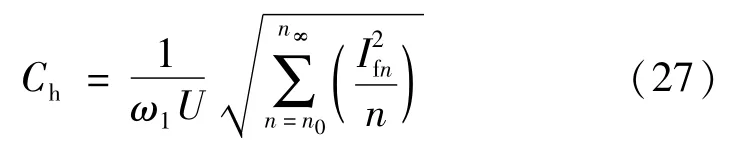
式中：Ifn为流过n次谐波电流的有效值。故电阻值、电感值分别为：

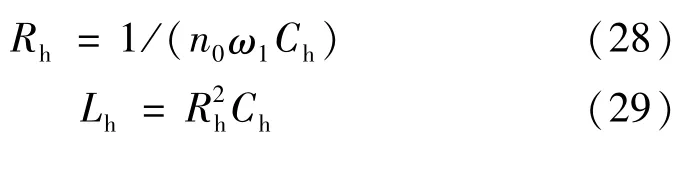
3 谐波补偿系统设计

3.1 谐波检测环节

SHAPF在稳态补偿时，其有源部分的直流侧只需要吸收负载谐波电流所引起的功率波动，在负载投入/切除等暂态过程中，负载的突变可能导致SHAPF直流电压的剧烈波动，严重时甚至会触发直流电压保护而使设备停机。

引起该问题的原因是负载突变时SHAPF检测环节输出的电流指令信号含有瞬态检测延迟引起的误差ei，检测环节的改进原则是设法消除ei，以减少SHAPF交直流侧非必要的能量流动，抑制直流电容电压的波动。本文采用文献［21］中所提方法，在检测环节加入二阶补偿器，其控制框图如图5所示。

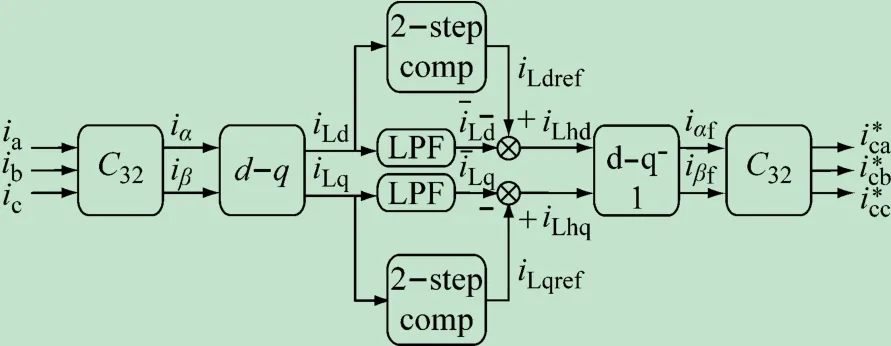
图5 含有二阶补偿器的谐波电流综合检测模块

图中，二阶补偿器的输出为：

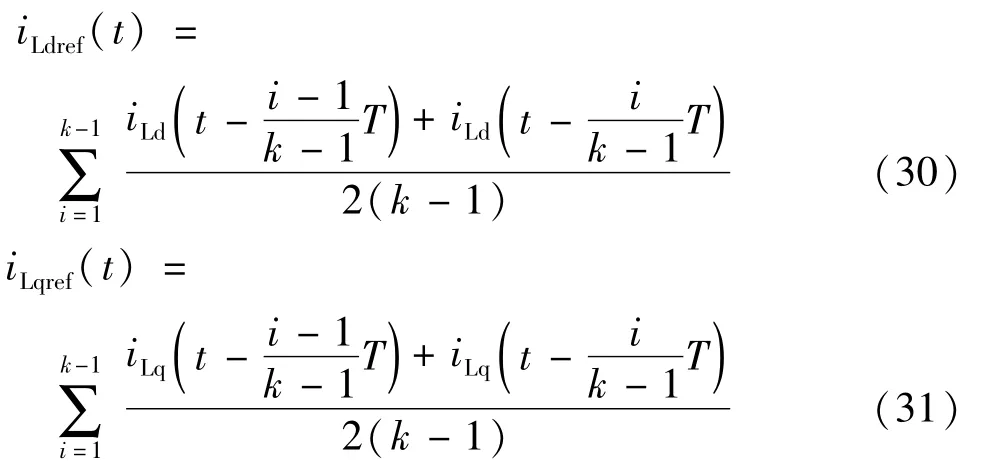
式（30）、（31）中取k=2。二阶补偿器使负载电流iLd，iLq的检测延迟与由滑动平均滤波器所引起的基波电流检测延迟保持一致，从而消除误差ei。由于负载突变所引起的直流电压波动小于稳态时的电压纹波，进一步提升了系统动态性能。

3.2 电流内环设计

SHAPF目前通常采用的滞环控制算法，由于定环宽设置容易造成控制变流器开关器件损耗较大，且输出电流中高次谐波含量较多，降低了电流的跟踪精度，在微网系统复杂谐波环境下补偿效果不理想［22-23］。

在传统滞环控制中加入动态控制环节，实时接收已有的三相电流传感器检测的补偿电流指令值和实际补偿电流ic，并根据其大小动态调节环宽阈值。

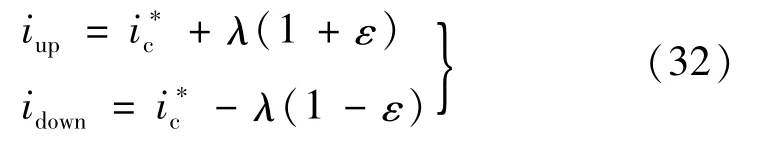
式中：iup为电流上阈值；idown为电流下阈值；λ为常数，大小为滞环宽度的一半。

故指令电流：

电流跟踪控制波形如图6所示。恒定开关频率的补偿电流控制器在不降低电流跟踪性能的同时解决了高次谐波问题，同时提高了开关器件的使用寿命，使变流器接收到的开关信号更加准确稳定。

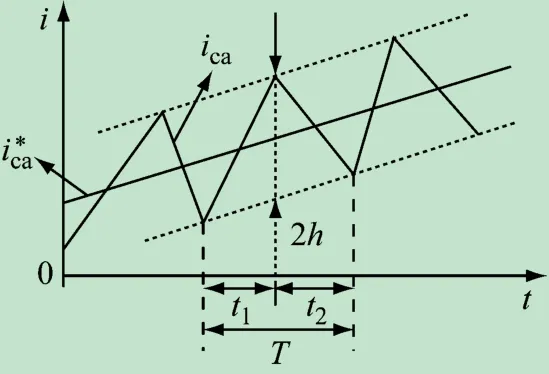
图6 放大后跟踪控制波形的几何关系

3.3 电压外环设计

由于微网系统的强非线性特征，存在谐波谐振和背景谐波放大问题，要求补偿系统具有更优的动态响应特性［24］。传统的直流侧电压控制方法是采用PI调节，但是PI调节参数范围较小，参数整定困难。自整定模糊PI调节能够使参数的整定时间大大缩短，动态性能优良，本文采用自整定模糊PI控制方法。将参考电压ucr和反馈电压ucf的差值Δudc作为模糊控制器的输入量e，将电压差值的变化率dΔudc作为输入量ec，并将PI调节器中比例系数的变化量ΔKp和积分系数的变化量ΔKi作为输出量，上述输入量和输出量的模糊论域均是［-6-4-2 0 2 4 6］，模糊集均是［NB NM NS ZO PS PM PB］。模糊子集中各元素的含义见表1。

表1 模糊子集中的元素含义

三角形隶属函数灵敏性较强，且易于实现，采用如图7所示的三角形作为输入、输出量隶属函数的形状。

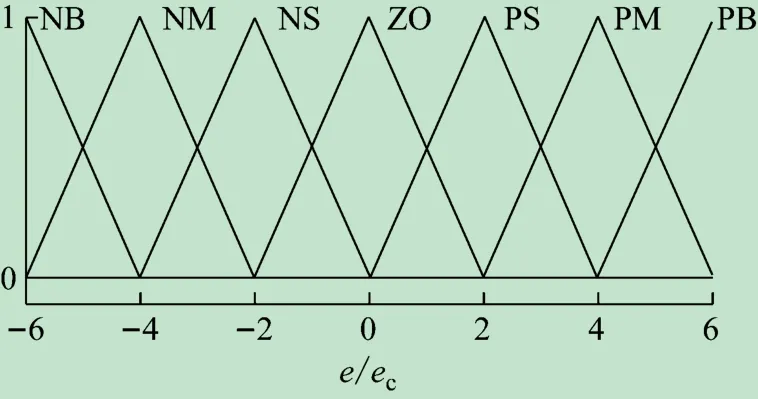
图7 输入输出量的隶属函数

电压差值e和电压差值变化率ec与PI调节器中参数Kp和Ki之间有如下关系：

（1）当e×ec＞0时，表明电压差值|e|在增大，为了使|e|减小，Kp应取更大的值，此时若Kp的值取得过大，为避免超调过大，Ki应取更小的值；

（2）当e×ec＜0时，表明电压差值|e|在减小，此时保持原来的控制作用即可；

（3）当e×ec=0时，如果电压差值e=0，保持原来的控制作用即可，如果电压差值e≠0，则说明直流侧电压反馈值的曲线和电压参考值的曲线平行，此时控制器应取更大的Kp和Ki，以使系统获得优良的静态特性。综上可得PI控制器的参数模糊规则控制表分别见表2、3。

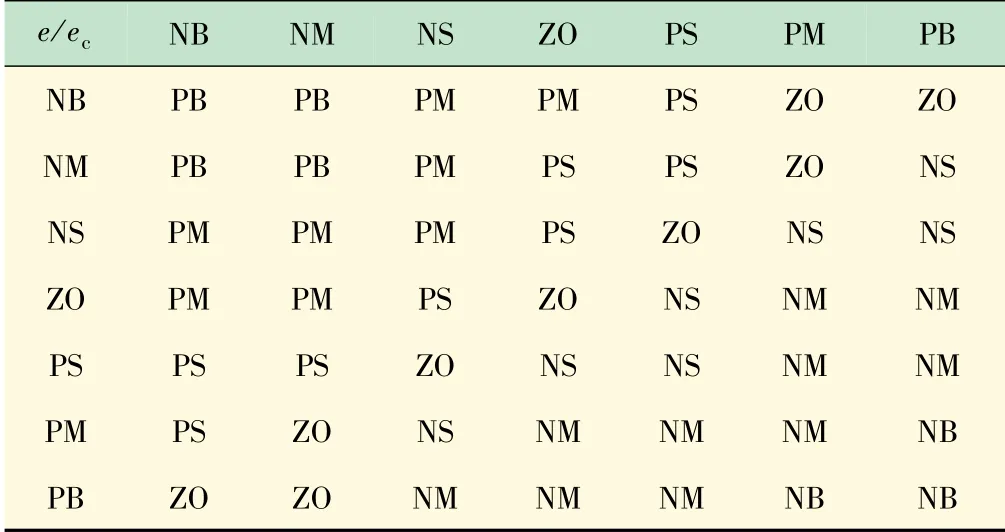
表2 ΔKp的模糊规则控制表

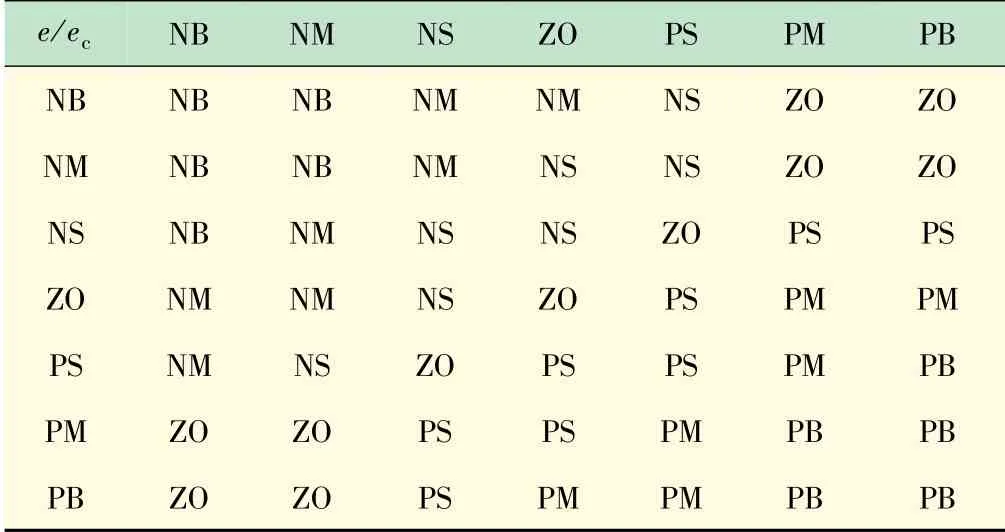
表3 ΔKi的模糊规则控制表

4 结果验证

为了验证前述方法的正确性，在Matlab/Simulink环境下建立两种SHAPF补偿系统的仿真模型。具体模型参数按表4～6设置，其中电容采用文献［25］中所提方法设计。

表4 系统参数

表5 APF参数

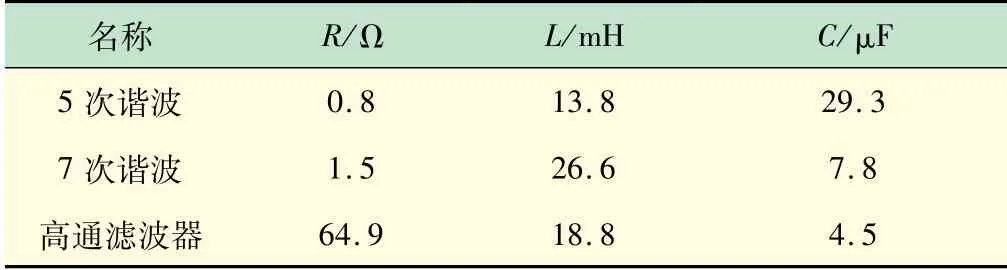
表6 PPF参数

系统在0.05 s时投入PPF后的补偿效果如图8（a）～（c）所示，由于PPF有效补偿了部分谐波电流，使电源电流畸变程度减小。

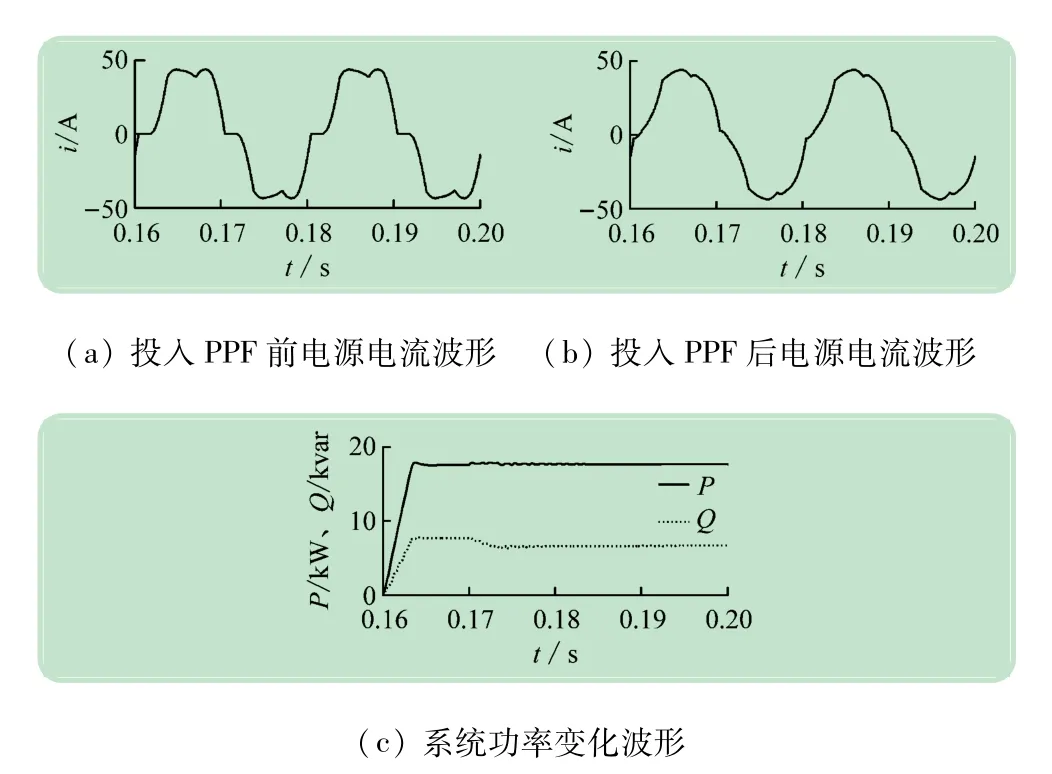
图8 电源电流波形及功率变化波形

投入PPF后电源电流总谐波畸变率（Total harmonic distortion rate，THD）从17.62%减小至9.08%，证明了PPF等效电路的有效性。PPF同时对无功功率进行了补偿，承担了大部分的补偿容量。

若投入单一的SAPF后补偿效果如图9所示，电源电流THD降至1.48%，显然SAPF具有比PPF更好的滤波特性，能够对系统进行快速准确的动态谐波补偿。传统的SAPF多用作低压系统的补偿，且这种单一SAPF的容量很大，成本较高，若还需补偿无功、负序等其他电能质量问题，将进一步增加系统容量和成本，这些问题制约了其在微网中的推广应用。

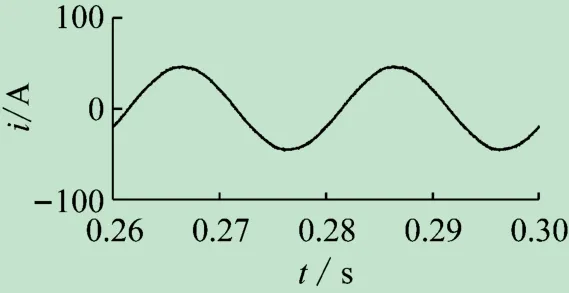
图9 投入单一SAPF后电源电流波形

投入改进的第1种SHAPF，结果如图10（a）所示，电源电流THD降至1.31%。由于这种混合型APF中有源元件需要补偿的电流很小，容量很小，该补偿系统比单一APF补偿系统更节约成本，适宜补偿大容量电流源型非线性负载。

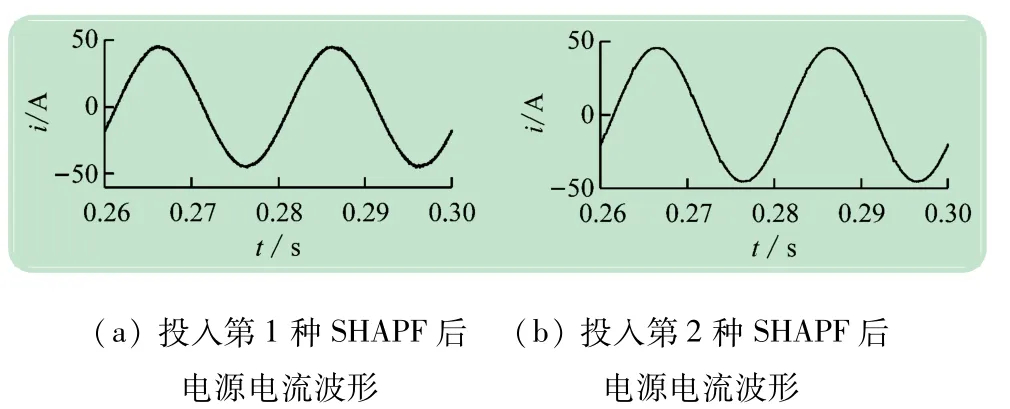
图10 投入两种SHAPF后的补偿效果

类似地，投入改进的第2种SHAPF，结果如图10（b）所示，电源电流THD减小至1.02%，补偿效果同样比单一PPF或并联APF的效果更好。这种结构中有源部分不承受基波电压、容量更小，因此适用于微网系统的谐波治理。

图11所示为投入两种SHAPF后的直流电压控制效果，可见本文对直流侧电压控制系统设计的正确性。为验证改进后系统的暂态性能，在t=0.16 s时突加负载，图12所示为系统a相电流波形，可见系统动态性能良好，没有出现电压电流的剧烈波动，补偿后电源电流THD=2.36%。

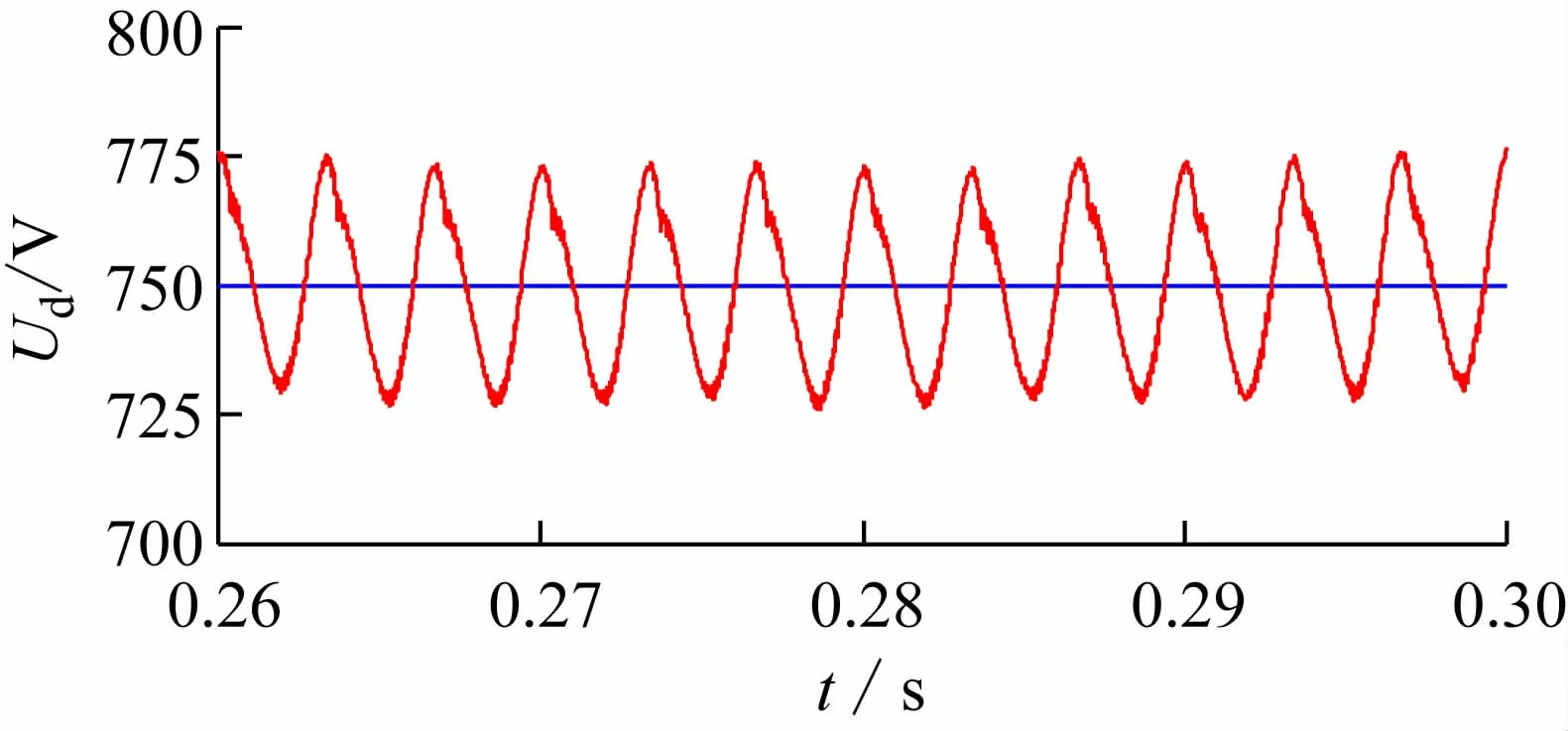
图11 投入两种SHAPF后的直流电压波形

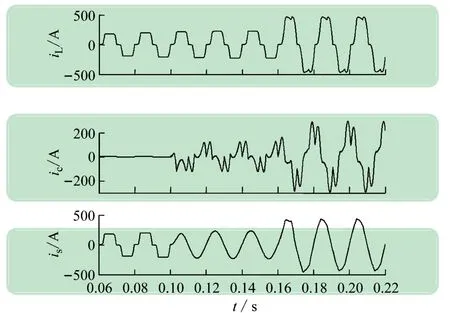
图12 负载突变时iLa、ica和isa的波形

5 结 语

本文建立了两种SHAPF补偿系统的等效电路，对主电路关键参数设计问题进行了详细探讨，使PPF承担了大部分的补偿容量，有效减小了有源功率单元的容量和成本。改进型双闭环控制系统动静态性能良好，仿真结果表明两种SHAPF补偿系统等效电路的有效性。第1种SHAPF结构适于大容量等效电流源型谐波负载的补偿；第2种SHAPF结构适用于高压系统，能够避免与系统间可能引起的谐振，适宜在微电网中推广应用。