检测钱德勒摆动周期和Q值的一种新方法
胥灿灿,方 明,许雪晴,周永宏,4,段鹏硕
(1.中国科学院 上海天文台,上海200030;2.麻省理工学院 地球、大气和行星科学系,美国02139;3.中国科学院大学 天文与空间科学学院,北京100049;4.中国科学院 行星科学重点实验室,上海200030)
1 引言
钱德勒摆动是地球自转的一个本征模。自1891年首次被发现以来,引起钱德勒摆动的物理机制和描述它的两个关键参数(周期和品质因子)一直是科学界关注的热点问题。空间大地测量技术为检测钱德勒摆动提供了丰富、高精度和高时空分辨率的观测资料,人们利用这些高精度的观测资料,在引起钱德勒摆动的物理机制有关领域的研究取得了很大进展,例如Smith和Dahlen[1]、朱耀仲[2−4]、Mathews等人[5],以及Chen等人[6,7]在理论上阐述了各种地球物理因素(如海洋、地幔粘弹性、核幔耦合等)对钱德勒摆动的贡献;Wahr[8]、Eubanks[9]、Barnes等人[10]、Gross[11,12]、Liao等人[13],以及Fang等人[14]研究了大气、海洋等地表流体激发钱德勒摆动的物理机制。尽管如此,由于理论假设的局限性[6]、部分观测数据的不确定性[15],以及观测数据的不完备性[8]等原因,到目前为止,引起钱德勒摆动的物理机制,摆动周期和品质因子的取值也一直没有明确的结论[16]。
由于钱德勒摆动与很多地球物理因素有关,因此,对其精确的检测具有很重要的科学价值。目前,关于钱德勒摆动周期和品质因子的计算和估计方法主要分为如下四类:
(1)谱分析方法。直接对极移观测序列进行谱分析,从而获得钱德勒摆动周期和品质因子[17−19]。
(2)随机激发假设方法。假设钱德勒摆动的激发机制是随机的,采用统计方法来估计钱德勒摆动周期和品质因子[20−24]。
(3)地球物理激发理论方法。采用实际观测数据,研究大气、海洋以及陆地水等地球物理机制对钱德勒摆动的影响[16,25−28]。
(4)半解析方法。基于一定的理论模型和实际观测资料,例如海洋、地幔、核幔耦合和三轴椭球等等,给出钱德勒摆动周期和品质因子的解析表达式[1,2−5,29]。
本文将前三类方法获得的周期和品质因子称之为观测值,将最后一类方法获得的称之为理论值。表1统计了现有方法对钱德勒摆动周期和品质因子的计算和估计结果。从表1可以看出,品质因子的参数估值具有极大的取值范围(36,1 000),尽管最新研究已经将其置信区间缩小至(56,255)[16],但仍然比较大。
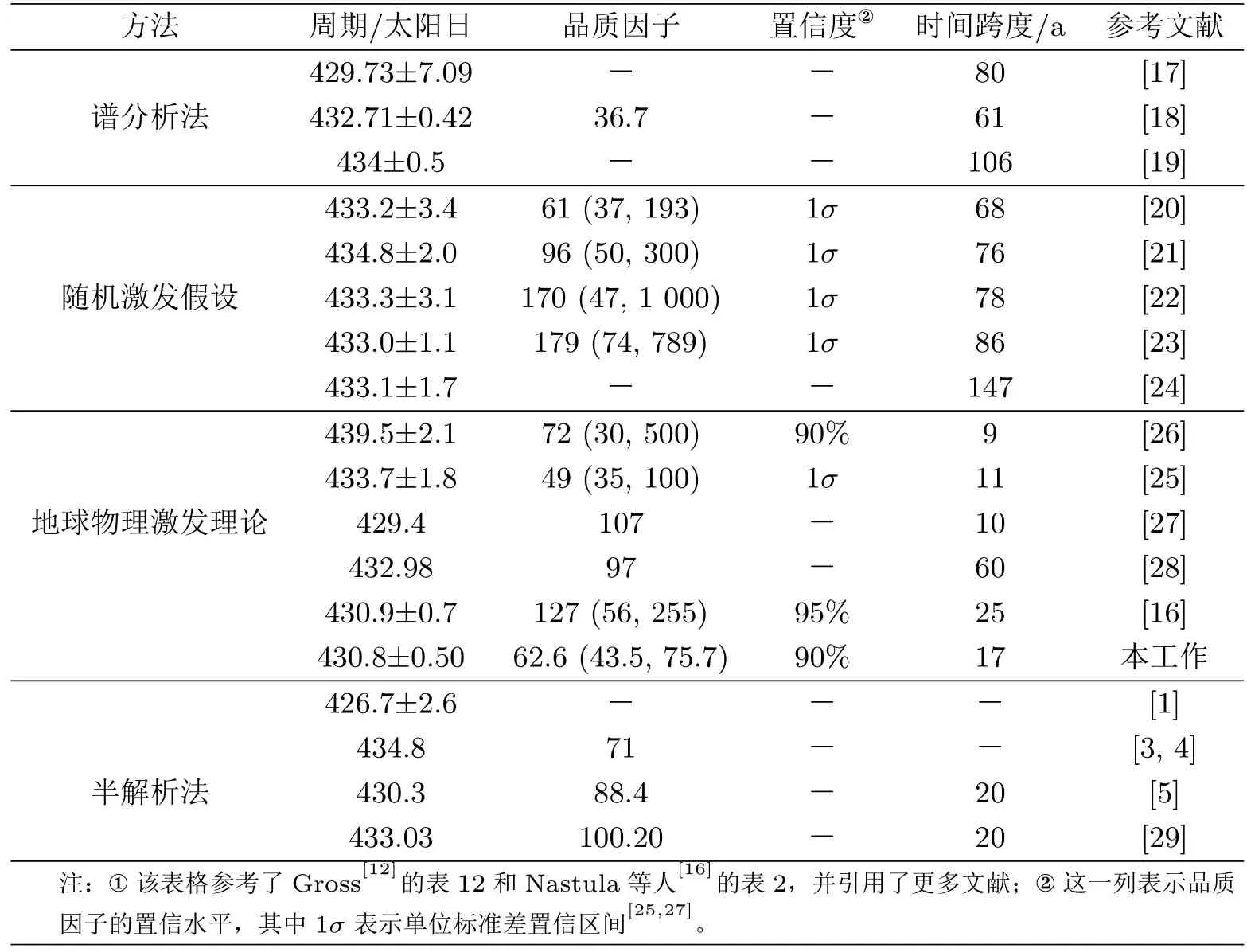
表1 钱德勒摆动周期和品质因子的点估计和区间估计的现有结论①
在前人工作基础上,本文创新性地提出了一种用于估计钱德勒摆动周期和品质因子的数学模型和快速算法。新方法对模型误差的假设更弱,估计结果的统计性质更优,新方法还采用了机制明确的优化算法,计算效率更高。
2 极移理论
假设地球不受外部天体的引力作用,在地固坐标系下,角动量定理可以写成刘维尔方程,即:

其中,ω是地固系相对惯性系的转动角速度。用Ω表示地球自转的平均角速度,则ω可以进一步表示为:

L是地球自转角动量,在地固系下,其表达式是

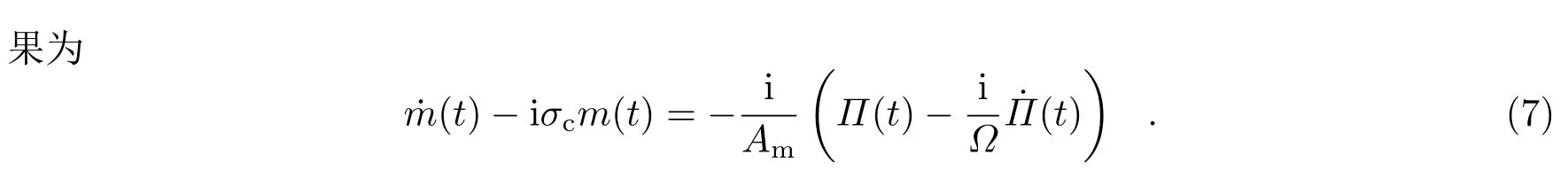
这里对式(7)做一点说明,传统处理方法是先对式(5)化简,再将其中的σcw替换为σc,即先化简再替换,如文献[31]中的式(13)和(14),而本工作则是先替换再化简。由于这两种处理方法对m(t)的影响不超过1%[8],并且观测数据的测量精度有限,所以可以认为这两种做法一致。考虑极移m(t)与观测极移p(t)的关系,可得[31]:

其中,p(t)=x(t)-iy(t),x(t)和y(t)就是由国际地球自转服务(International Earth Rotation and Reference Systems Service,IERS)或其他组织和机构提供的极移观测序列,其中y(t)以指向90°W为正。将式(8)代入到式(7)中,可得

对这个微分方程进行求解,其中p(t)的自由项在经过很长一段时间后逐渐衰减消失,只剩下受迫激发项,因此p(t)的解析表达式为:
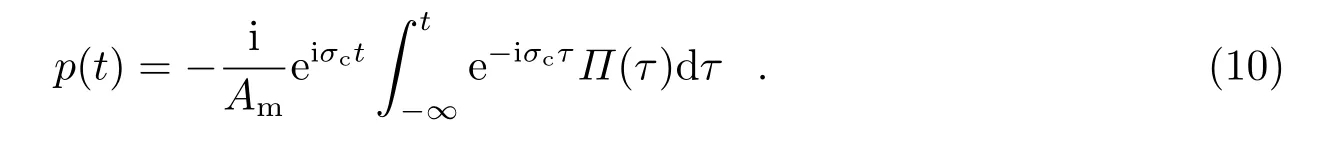
3 估计算法
基于式(10),本章对误差进行基本假设,提出用于估计Tc和Qc的数学模型;同时,基于这些误差假设和新的数学模型,引入Tc和Qc的区间估计方法——自助法。
3.1 估计T c和Q c的快速算法
假设数据是等间隔采样的,采样间隔为δt,数据长度为N,初始历元为t0。根据式(10)可以给出离散数据满足如下一阶自回归形式:
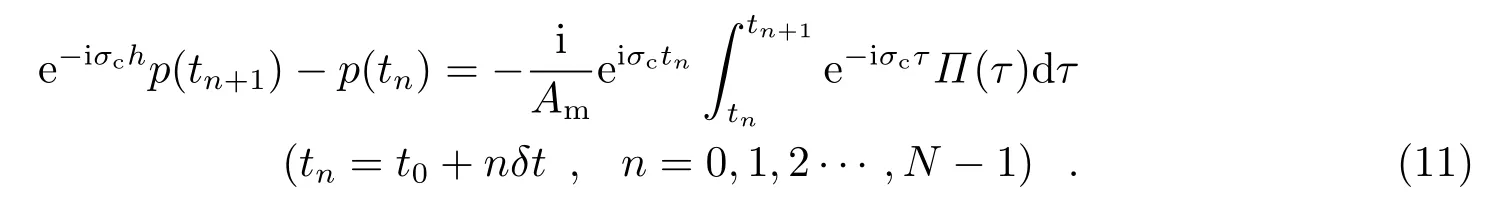
考虑到Π(t)不完全是大气和海洋的角动量,可能还包含了不可观测的和未知的因素,如在式(6)的h(t)和ΔI(t)中,它们不仅包含了地表流体的作用,还包括了地球内部的作用(如地磁急变[19]),而后者不可直接观测[8]。所以,可以将Π(t)分解为如下三个部分:

其中,Πobv(t)+Πerr(t)是可观测部分的真值,Πobv(t)是与之对应的实际观测数据,Πerr(t)是观测数据的测量误差(即观测误差);Πres(t)是上面提到的其他不可观测的或未知的激发源。这里将式(12)的后两项合并,记为Πmer(t),简称模型误差。最后,假设模型误差对应的离散序列Πmer(tn)是一个均值函数为0、一阶自相关函数为0的随机噪声。
将Π(t)=Πobv(t)+Πmer(t)代入式(11)中,对关于Πobv(t)的积分用辛普森公式展开,而对关于Πmer(t)的积分用梯形公式展开,并引入以下表达式:
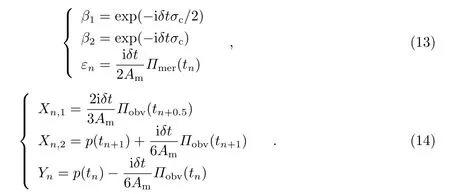
利用式(13)和(14)将式(11)展开并化简为:
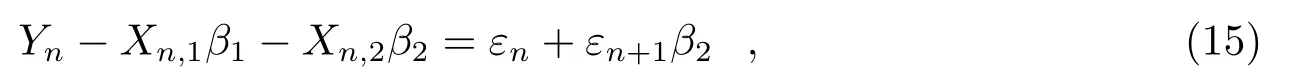
其中,n=0,1,2,···,N-2。引入矢量Y,X1,X2,ε和˜ε,式(15)可以被改写为回归方程的形式:

考虑到序列Πmer(tn)的一阶自相关函数为零,因此εH˜ε=0成立(上标H代表矢量的共轭转置),可以获得残差平方和的解析表达式:


总之,该方法采用了一种机制明确的算法来直接获得最优的ˆTc和ˆQc,而不用在某个特定区域内比较每个网格点上的结果,例如Nastula和Gross[16]采取的方法(下面将其简称为网格搜索法),因此本方法具有更高的计算效率。
3.2 区间估计的方法——自助法
目前关于钱德勒摆动周期和品质因子的区间估计都是基于蒙特卡洛方法开展的[16,25],这种方法需要事先获取模型误差Πmer(t)的理论分布。根据式(12)可知:Πres(t)是未知的或不可观测的,假设它服从任何一种分布可能都不合理;此外,随着观测水平的提高,观测数据的测量精度也在逐渐提高,因此观测误差Πerr(t)具有异方差性。综合这两个因素可以发现,理论模型难以描述Πmer(t)的分布函数,因此蒙特卡洛方法的区间估计结果可能不够精确。
基于此,本工作采用自助法(Bootstrapping)做区间估计,该方法的优势是不需要知道Πmer(t)的分布函数。自助法是一种现代的非参数统计方法,最早由Efron[32]提出,经过近几十年的发展,它已经具备了扎实的理论背景并拥有广泛的应用范围[33]。自助法的操作流程简捷,具体为:(1)将包含K个样品的初始数据集当做总体,每次从中有放回地抽取K个样品,如此重复B次,就得到了B个新样本;(2)对每个再抽样的样本分别做参数估计,可以得到每个参数的B个估值;(3)基于这B组估值,可以给出基于初始数据集的区间估计,甚至研究参数估值的有效性。
本工作采用自助法来对Tc和Qc进行区间估计,按照以上步骤将式(15)中的N-1个方程当成总体(这一做法在参考文献[33]中有详细的描述),每次从中有放回地抽取N-1个样品,然后根据式(16)―(21)对再抽样的样本做参数估计,如此重复多次,可以获取多组Tc和Qc的参数估值,据此给出Tc和Qc的区间估计结果。
4 数据及预处理
对于极移观测序列,我们采用Ratcliff和Gross[34]解算的COMB2018数据集,该数据集在1990年后的时间段具有非常高的精度。大气角动量(atmospheric angular momentum,AAM)数据来自美国国家环境预报中心/大气研究中心(National Centers for Environmental Prediction/National Center for Atmospheric Research,NCEP/NCAR)数据集[35],该数据集考虑了地形因素的影响,精度更高[36]。海洋角动量(oceanic angular momentum,OAM)数据来自IERS特殊海洋局(Special Bureau for Ocean)的ECCO-kf080i数据集。这三个数据集的采样间隔都是1 d,选取的公共时间跨度为1993/01―2018/12。在参数估计之前,对这些数据做如下预处理[16,25]:
(1)扣除三个序列中的周年项、季节项和线性趋势项。采用最小二乘法从原始序列中扣除频率为1,2,3,4,5,6,7,8 cpy的谐波信号,两个周期分别为13.661 d和13.633 d的潮汐项,一个一阶多项式函数。
(2)扣除低频项。除线性趋势项外,极移序列中的低频信号一般被认为来自地球内部,而这些激发源不能被直接观测,据此设计一个高通滤波器,过滤掉三个序列中周期大于2 a的频段。
预处理后的数据展示在图1中,从该图可以看出:钱德勒摆动的振幅一直处于调制中,总体在减小,而在2010―2019年期间,钱德勒摆动的振幅已经减小到非常显著的程度(这也可以在Wang等人[37]的图8中得到验证);对于预处理后的角动量序列,与平稳随机噪声非常相似,并且实部振幅比虚部振幅稍小。
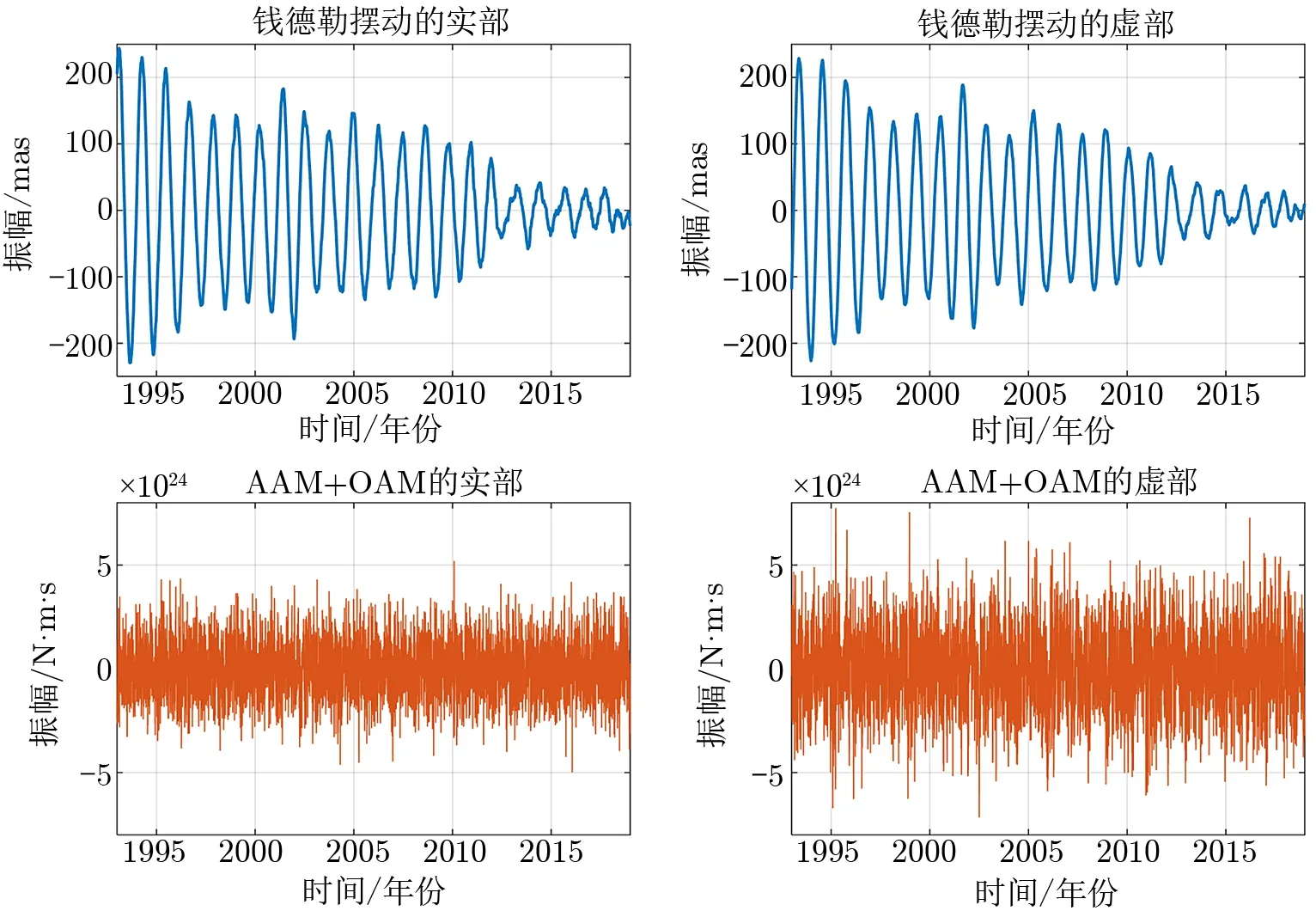
图1 预处理后的数据序列图
5 结果
为了更全面地评估新方法的稳定性和可靠性,本工作选用三个不同的时间段对研究结果进行分析和讨论,分别是1993―2010年、2000―2019年和1993―2019年。在每个时间段都使用自助法做1 000次再抽样,每个时间段都得到1 000组ˆTc和ˆQc。这3 000组估计值的统计直方图如图2所示,它们的均值、方差和90%置信区间如表2所示。
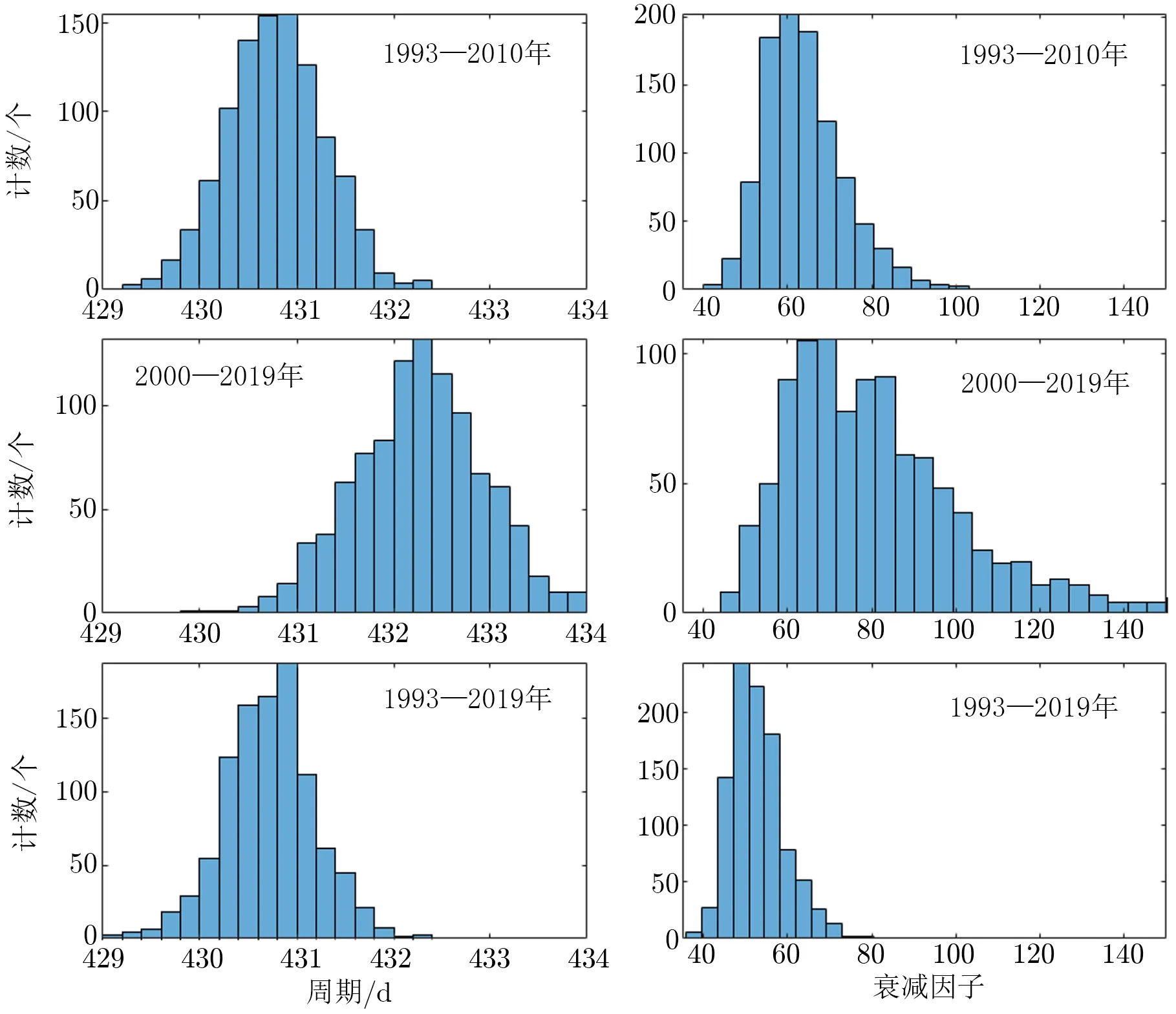
图2 3 000组周期和品质因子的参数估计值的统计直方图

表2 3 000组周期和品质因子的参数估计的均值、方差和90%置信区间
从图2和表2的统计结果可以看出,第一个时间段(1993―2010年)和第三个时间段(1993―2019年)给出的Tc和Qc的区间估计几乎是重合的,并且ˆTc的方差很小;对于Qc的估计,其对数据的选择比较敏感,这也是现有估计方法共同的问题(如表1所示)。对比表1和表2可以看出,新方法对Qc的估计具有更小的方差,显示了更优的统计有效性。
从图2和表2的统计结果还可以发现,第二个时间段(2000―2019年)与其他两个时间段的参数估计结果差距较大。这可能与近年来钱德勒摆动的振幅逐渐减小有关,该时间段的估计结果可能具有一定的系统性偏差,我们将在未来的研究中进一步探讨。
综合以上结果,可以确定第一个时间段(1993―2010年)的参数估计更加合理,即Tc和Qc的点估计为430.8 d和62.6,两者的90%置信区间分别为(430.0,431.6)d和(43.5,75.7)。在该时间段内的参数置信区间更宽,具有更大的概率包含Qc的真值,是一个比较保守的估计。此外,这一结果与Mathews等人[5]及Nastula和Gross[16]的结果很接近,再一次验证了新方法的可靠性。
6 总结与讨论
本文从经典的极移理论出发,给出了一种用于估计钱德勒摆动周期和品质因子的新方法。新方法对于误差的假设较弱,并采用更加合理的自助法进行区间估计,参数估计的结果具有更优的统计性质。此外,新的点估计算法采用了机制明确的双点割线法来直接获取最优解,与传统的网格搜索法相比具有更高的计算效率。
对地球钱德勒摆动周期和品质因子的最优点估计结果分别为:430.8 d和62.6,两者的标准差为0.50 d和9.63,最优的区间估计分别为(430.0,431.6)d和(43.5,75.7)。这一结果与Mathews等人[5]及Nastula和Gross[16]的结果很接近,且我们的参数估值具有更小的方差,再次验证了新方法的可靠性和优越性。
由于目前只采用了大气和海洋的角动量数据,对地球钱德勒摆动周期和品质因子的最优估计可能还存在一定偏差。未来我们将考虑陆地水或全球水文角动量的影响,进一步提高钱德勒摆动周期和品质因子的估计精度。此外,随着对钱德勒摆动认识的逐步提高以及观测数据的精度提升,本工作提出的新方法将对地球钱德勒摆动的精准预报提供可能。
致谢
感谢两位审稿人对本文的肯定,他们提出的意见和建议也十分宝贵,这大大提高了文章的质量和可读性。与上海天文台廖新浩老师的交流讨论让我们受益匪浅,感谢廖老师在这个过程中提出的建设性意见,这促使新方法改进得更加完善。

