基于熵权-GRA-TOPSIS的组合评价模型在黑龙江省城市经济发展综合评价中的应用研究*

祖培福，姚 尧，马 妍

(牡丹江师范学院)

0 引言

区域经济发展的不平衡、不协调作为一个世界范围内普遍存在的现象，对地区的经济发展、民族团结及人民生活水平都会产生较为不利的影响.因此若对一个地区城市的整体经济发展水平能给出尽可能客观定量的综合评价，以了解每个城市的经济发展水平在整个地区的位置，对于促进整个地区经济的协调发展都具有重大的现实意义与应用价值.

近年来，对区域经济发展的综合评价这一问题的研究，许多学者用各种不同的方法对特定区域的评价取得了较为丰厚的成果[1-5]，而随着对系统评价方法研究的深入，学者们发现运用不同的单一方法对同一系统做评价时，评价结果有时会存在着一定差异，且每种方法都有自己的优缺点.虽然在实际评价时很难指出哪种方法最好，但学者们能基本达成共识的是进行评价时若只用单一方法会使结论具有一定的片面性，并认为多种单一方法的组合应用能够有一定的优势互补会使得评价结论会更加全面客观[6].所以利用组合评价模型在经济、管理、工业及教育等各个领域的许多方面的评价研究都取得了更为丰硕的成果[7-11].该文也是考虑到组合评价模型在多指标评价系统中的优势，将能客观确定指标权重的熵权法，单一评价方法的理想点法(TOPSIS)及灰色关联分析法(GRA)进行有机结合构建出灰色理想值逼近模型，并利用该模型对黑龙江省的12个主要城市的宏观经济发展水平进行综合评价，可为政府等相关决策部门制定相应的发展规划政策提供定量的参考资料.

1 组合评价模型的建立

1.1 预备知识

考虑具有m个评价对象，n个评价指标的待评价系统，记Xm×n=(xij)m×n，其中xij(i=1,2,…,m;j=1,2,…,n)为第i个评价对象的第j项指标值，而由于不同评价指标量纲的不同，可由式(1)作标准化处理：

(1)

从而可得到对数据标准化处理的决策矩阵：

Zm×n=(zij)m×n.

1.2 评价指标权重的确定

熵值法[6]是通过对各项指标自身所提供的信息量大小的比较来确定指标权重大小的一种客观赋权法，不同评价对象指标间差异越大则指标区分评价对象的能力就越强，可用熵值来衡量指标信息量大小所引起的差异，用熵权法确定指标的权重具体如下：

(1)求出第j项指标下第i个评价对象的特征比重pij：

(2)

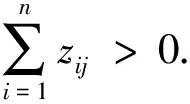
(2)求出第j项指标的熵值ej:

(3)

(3)计算第j项指标的差异系数hj:

hj=1-ej

(4)

hj越大越应重视该指标，对应的指标权重也就越大.

(4)计算指标权重系数wj:

(5)

1.3 GRA-TOPSIS的灰色理想值逼近模型

理想点法(TOPSIS)是通过对有限多个评价指标的评价对象与正负理想目标(也可称作最优与最劣参考目标)距离的接近程度排序进行相对优劣的评价.该方法计算较为简便，结果客观，但有一定的局限性，如可能会出现评价对象与正负理想点都接近的情况，这样就不能很好的反映评价对象的优劣性；而灰色关联法(GRA)以灰理论为基础，通过寻找最优指标数据作为理想解，然后通过比较各评价对象与理想解的关联程度来反映评价对象的优劣.该方法对数据分布规律与样本量不作限制，但结论不够精确且容易受到评价对象全局极值的变化影响.从而通过分析上述两种单一评价方法的优缺点并同时发挥两种评价模型的优势，考虑将两种评价方法进行结合来构建以计算各评价对象的灰色关联贴进度的灰理想值逼近模型.具体如下：

(1)通过决策矩阵Zm×n=(zij)m×n找出其正负理想评价对象(最优与最劣参考目标)，分别标记为：

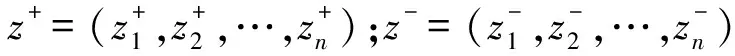
(6)

(2)分别计算各评价对象与正负理想目标的灰关联系数矩阵，分别记为：

(7)

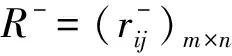
(8)

式中ρ为分辨系数，0<ρ<1，一般取ρ=0.5.

(3)计算各评价对象与正负理想目标的熵权灰色关联度如下：

(9)

(4)计算各评价对象的灰关联贴进度Qi:

(10)

灰关联贴进度Qi越大表示评价对象越优，反之显示评价对象越劣.

2 黑龙江城市经济发展水平综合评价的实证分析

2.1 评价指标体系的建立与数据的标准化处理

该文选取黑龙江省的包括哈尔滨市、齐齐哈尔市及牡丹江市等在内的12个主要城市为评价分析对象，经济发展评价指标的选取依据科学发展观的要求及能反映系统性、科学性及可测性原则基础上并根据现有文献资料中对该问题研究使用频率较高的指标为主，并进一步考虑到指标数据的实际可得性，选取了城市人均GDP(元)、固定资产投资额(亿元)、国内贸易额(亿元)、对外经济总额(亿元)、第一产业增加值(亿元)、城镇家庭年人均可支配收入(元)、第二产业增加值(亿元)、财政收入(亿元)、金融机构本外币各项存款余额(亿元)及第三产业增加值(亿元)并将这些指标依次标记为：X1、X2、X3、X4、X5、X6、X7、X8、X9、X10，原始数据主要来自统计年鉴及各城市经济与社会发展统计公报.将原始数据依据公式(1)进行标准化处理，结果见表1.

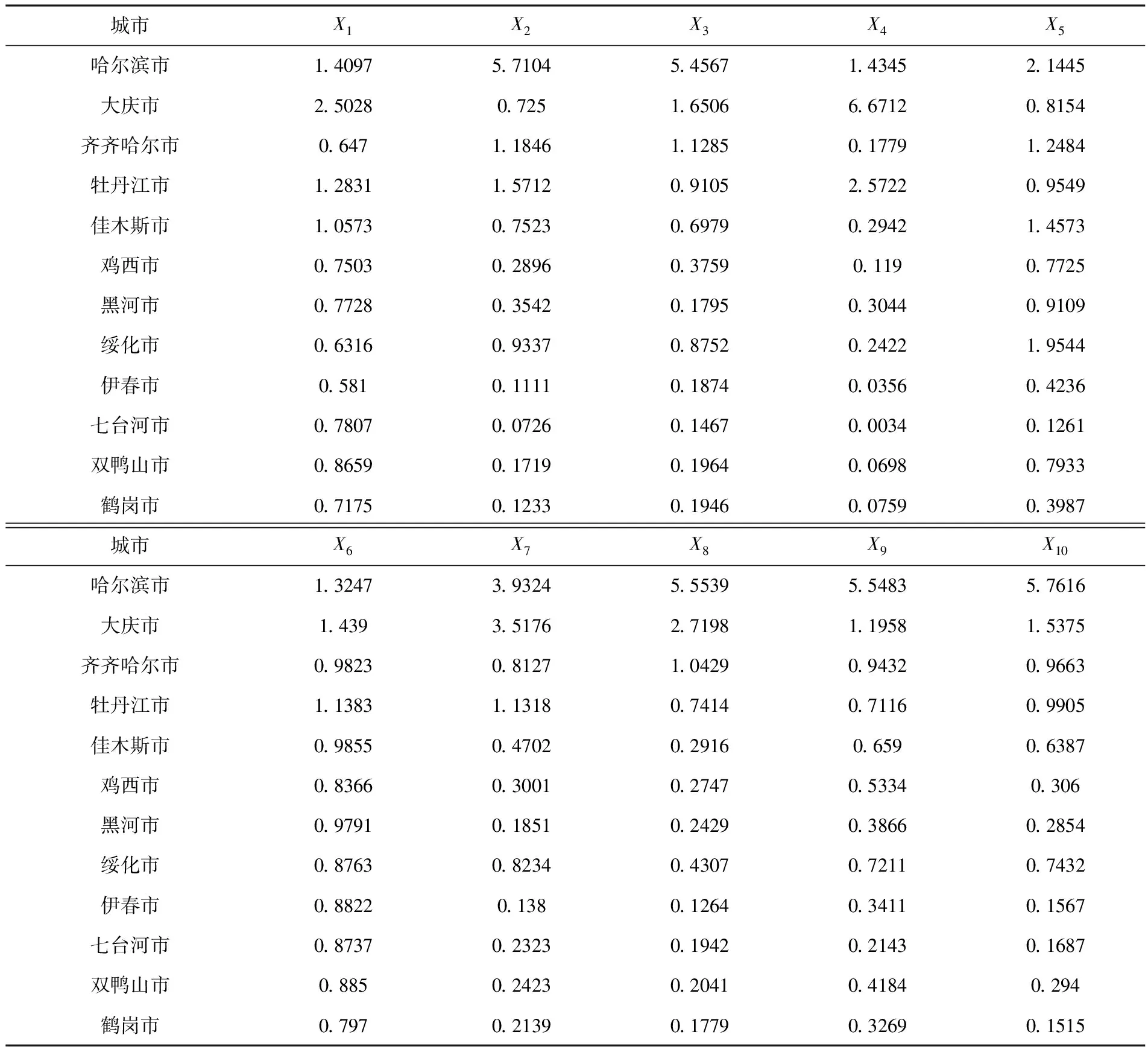
表1 黑龙江省12个城市宏观经济发展水平指标数据的标准化结果

2.2 确定各经济发展评价指标的熵权系数

将表1中数据带入公式(2)、(3)，(4)及(5)计算出各指标相应的熵值、差异系数及指标权重，结果见表2.

表2 十项城市经济发展的宏观经济指标熵权系数

2.3 计算各城市与最优及最劣参考序列的关联系数

首先通过表1中的指标数据并利用公式(6)得出指标数据的最优与最劣参考序列，见表3，然后将表1中各评价对象与表3的最优与最劣参考序列通过公式(7)与(8)得到优关联系数见表4及劣关联系数见表5.

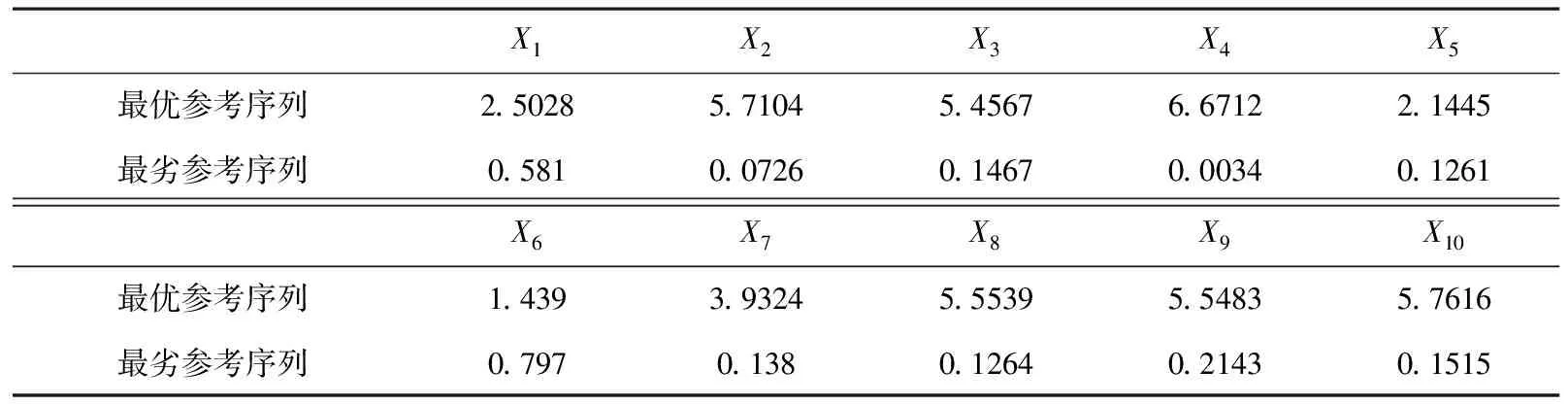
表3 指标数据的最优与最劣参考序列

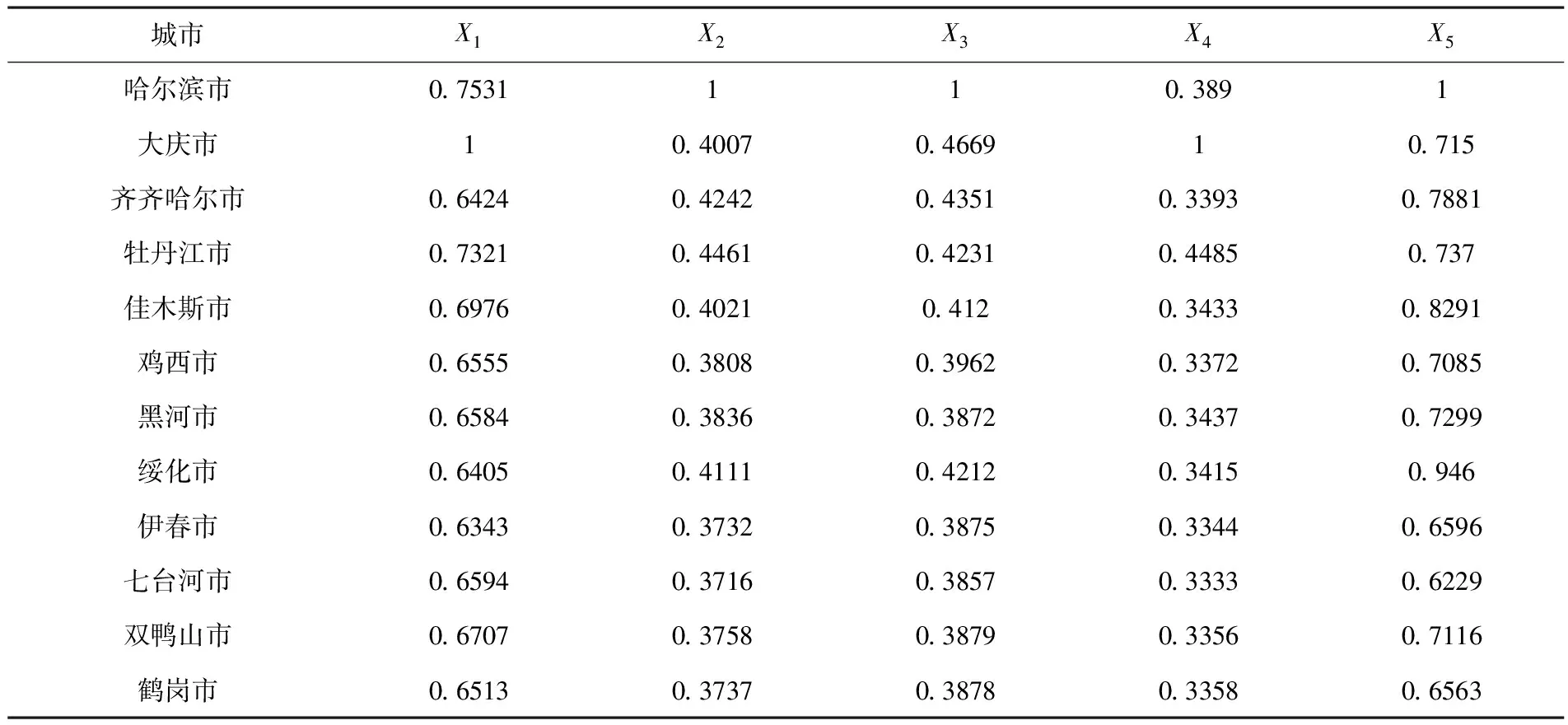
表4 黑龙江省12个城市与最优参考序列的优关联系数

续表4

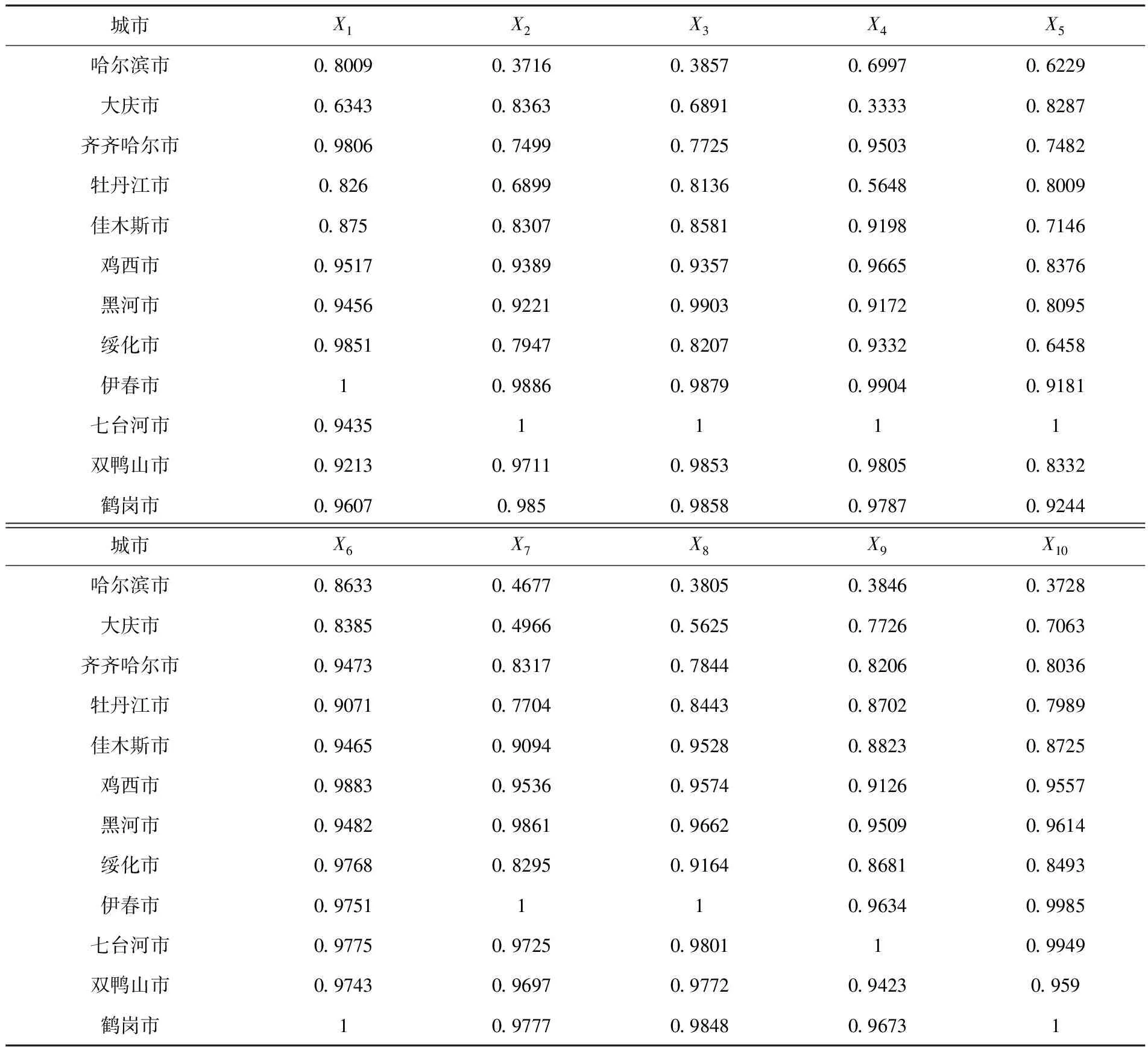
表5 黑龙江省12个城市与最劣参考序列的劣关联系数

2.4 计算各城市经济发展的灰关联贴进度

通过表2中各指标熵权系数及表4、表5中优劣灰关联系数利用公式(9)、公式(10)得到黑龙江省各城市与最优及最劣目标的优劣关联度得分及最终的灰关联贴进度，结果见表6.

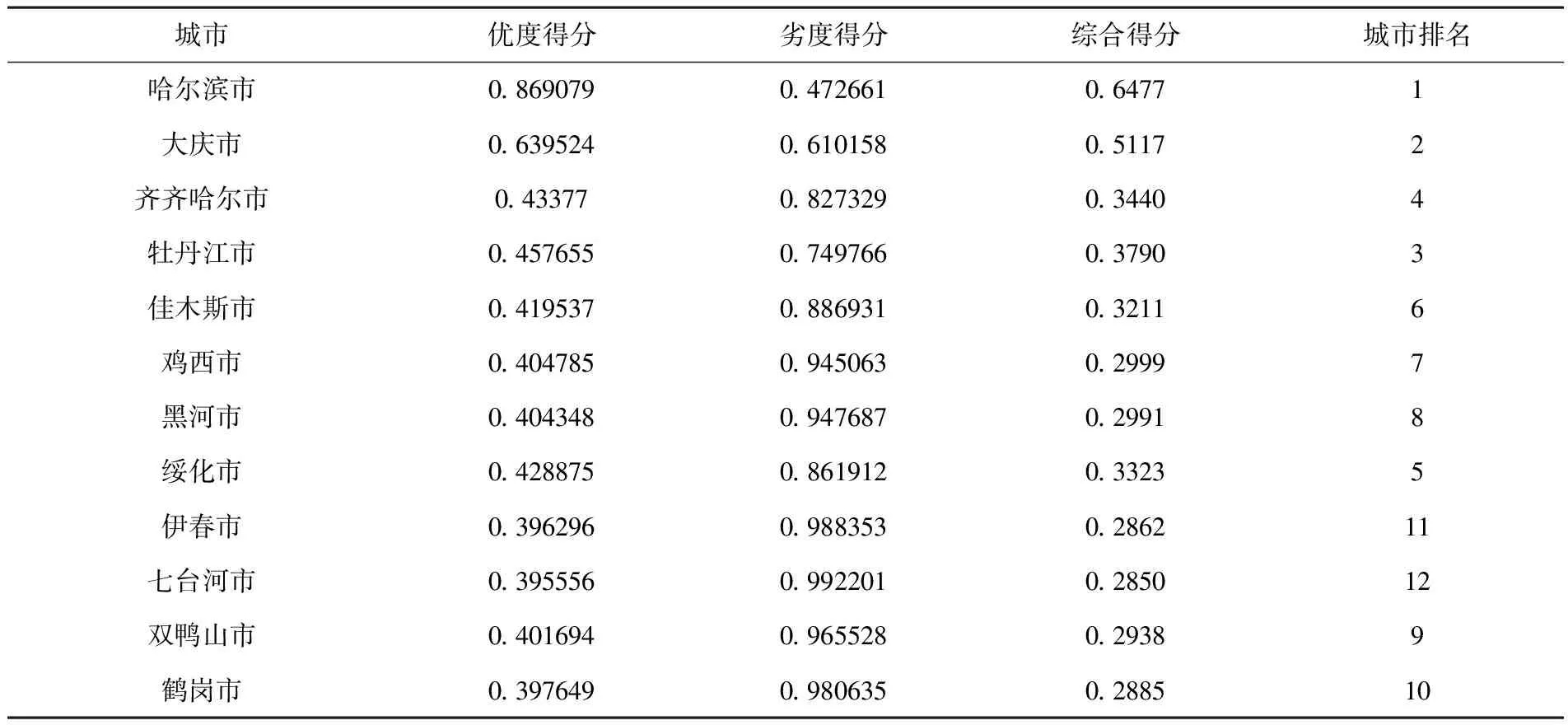
表6 黑龙江省12个城市经济发展水平的综合实力排名

依据表6各城市经济发展的灰色关联贴近度得分得出黑龙江省12个城市经济发展的综合实力排名顺序依次为：哈尔滨市>大庆市>牡丹江市>齐齐哈尔市>绥化市>佳木斯市>鸡西市>黑河市>双鸭山市>鹤岗市>伊春市>七台河市，从而可以看出哈尔滨市、牡丹江市、齐齐哈尔市及大庆市的经济发展水平在黑龙江所有城市中排名上等，而哈尔滨市作为省会城市其经济实力最强，从最终评价值也能看出其发展速度远远高于其他城市；绥化市、佳木斯市、鸡西市及黑河市的经济发展水平处于中等位置，说明这几个城市在全省来看是相对平稳的发展；而双鸭山市、伊春市、鹤岗市及七台河市这几个城市的经济发展水平在黑龙江所有城市中排名处于落后位置，显示这几个城市的经济发展较为缓慢，其中七台河市的经济发展水平最低，处于上述12个城市的最后一名.

3 总结

该文针对区域城市经济发展水平的综合评价问题为切入点，考虑到单一评价模型在评价时可能出现不足及理想点法与灰色关联分析法各自的优势，将二者结合起来构建了基于熵权下的组合评价模型，并以黑龙江省城市经济发展水平的综合评价为例进行了实证分析.该方法亦可推广到公司企业的员工评优、晋职及全面的绩效考核等方面，具有较强的应用价值.