基于克里金代理模型与子集模拟的边坡高效可靠度分析

雷世平，李京泽，刘磊磊*，李云青

（1.湖南省有色地质勘查局一总队，湖南 郴州 423099；2.有色金属成矿预测与地质环境监测教育部重点实验室（中南大学），湖南 长沙 410083；3.湖南省有色资源与地质灾害探查湖南省重点实验室，湖南 长沙 410083；4.中南大学地球科学与信息物理学院，湖南 长沙 410083）

0 引言

近年来，基于概率论与统计学的可靠度分析方法在边坡稳定性分析中得到了广泛的应用［1-6］。可靠度分析方法将岩土体中客观存在的不确定性纳入边坡稳定性分析框架当中，提高了对边坡安全性与可靠性评估的准确性与全面性［7］。传统可靠度分析方法一般通过蒙特卡洛模拟对边坡失效概率进行计算，但该方法由于需要反复进行大量的边坡稳定性分析，从而存在计算效率低下、计算资源占用过大的问题。针对该问题，代理模型作为提高计算效率、节省计算资源的方法逐渐受到了关注，该类方法一般采用简单的显式函数或模型代替复杂的边坡稳定性分析，避免了蒙特卡洛模拟中复杂且高度非线性的边坡稳定性分析模型的重复计算，从而极大地提高了可靠度分析的计算效率［8］。

目前常用的代理模型方法有传统响应面法［9］、多重响应面法［10］和克里金法［11］等。其中，克里金代理模型由于其在计算灵活性和准确性方面的优势而在可靠度分析方法中得到了广泛的应用［12-14］。例如，GASPAR等［14］提出该方法不仅可以提供未采样点的估计值，而且可对未采样点的估计误差进行量化，进而推动其在边坡可靠性分析与不确定性量化中的应用。LIU等［15］提出了一种自适应克里金模型，通过在大多数不确定点逐一选取训练样本，达到用最少的样本拟合边坡稳定性分析的目的，克服了其它模型随机选取训练样本而计算耗时的不足。同时，为了提高克里金模型在边坡可靠度分析中的适用性与准确性，多种全局优化算法如人工蜂群算法［16］、遗传算法［11］和粒子群优化算法［17］近年来亦被用于优化克里金模型参数。总之，虽然克里金方法可以有效地用于边坡可靠度分析，但当边坡处于小失效概率水平（如失效概率＜10-7）时，传统蒙特卡洛模拟处理高维矩阵时可能导致计算机内存溢出，造成可靠度计算求解困难，从而限制了克里金模型在边坡可靠度分析中的适用性。

为解决上述问题，本文在建立边坡稳定性克里金代理模型的基础上，提出结合子集模拟方法开展高效的边坡可靠度分析。在该方法中，子集模拟被用于替代传统克里金可靠度分析中的蒙特卡洛模拟，使得计算矩阵维度大大降低，从而提高计算效率。

1 高效边坡可靠度分析方法

克里金方法是一种利用邻近已知位置观测数据进行空间最优线性预测的方法，可对区域化变量求最优、无偏内插估计值［18-19］。该方法通过假设已知点与未知点之间的距离或方向来反映已知点和未知点之间的空间相关性，并通过高斯过程建模对于插值点进行预测。在边坡可靠度分析中，克里金法以土体参数（如抗剪强度）及边坡响应（如安全系数）为输入变量进行参数建模，随后将所建立的克里金模型作为代理模型取代耗费计算资源与计算时间的传统确定性分析模型，进而估计边坡失效概率。本文中，克里金模型的建立是通过基于MATLAB的开源代码DACE工具箱进行实现［20］。

为降低输入变量的矩阵维度以解决小失效概率边坡的可靠度分析与计算效率问题，本文使用子集模拟代替直接蒙特卡洛模拟进行边坡失效概率的计算。子集模拟作为一种高效蒙特卡洛模拟方法通过一系列具有较高概率的中间失效事件的概率乘积来表达一个小概率的失效事件F。在边坡稳定性分析中，边坡的安全系数为临界滑面（即所有潜在滑面中安全系数最小的滑面）的安全系数。由此，边坡的功能函数如下：

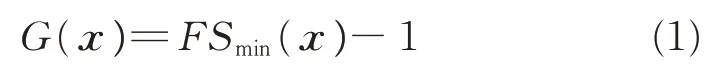
式中：x——随机变量，如土体抗剪强度（粘聚力c、内摩擦角φ）；FSmin(x)——边坡临界滑面的安全系数；G(x)——边坡功能函数，其反映了边坡的稳定状态，当G(x)≥0时，边坡保持稳定状态，反之当G(x)＜0时，则认为边坡失稳。

在边坡可靠度分析当中，边坡的失效概率Pf表述如下：

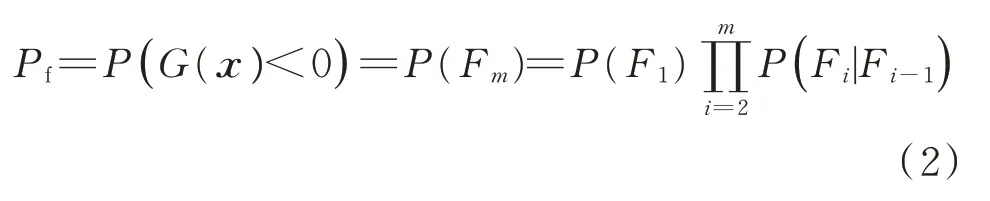
式 中：P(·)——事 件 的 概 率；Fi={G(x)＜gi(x)，i=1，2，…，m}——一组中间失效事件，这些事件由阈值FS值的递减序列g1(x)＞g2(x)＞…＞gm(x)定义；m——子集模拟的层数。

在计算过程中，gi(x)通过对前一个中间失效事件Fi-1=G(x)＜gi-1(x)的条件样本的统计分析来确定。其中，临界阈值gi(x)使得中间失效事件所对应的失效概率均为设定的特定的条件概率值p0。据LIU等［21］与LI等［22］，子集模拟中的初始蒙特卡洛样本数N0=500与条件概率p0=0.1可同时兼顾计算精度与计算效率，因此本文子集模拟中均按照此值进行设定。通过以上方法计算可得边坡失效概率，随后可参考《建筑结构可靠性设计统一标准》（GB 50068—2018）［23］（表1）根据边坡安全等级进一步确定边坡的加固与处理方法。

表1 建筑结构安全等级及相应可靠度指标与失效概率[21]Table 1 Building structure safety grade and corresponding reliability index and failure probability

2 计算流程

本文提出的边坡可靠度分析的计算流程如图1所示，主要步骤如下：

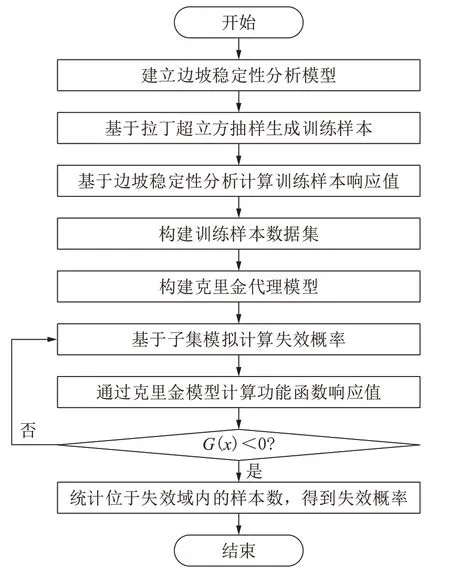
图1 基于子集模拟与克里金代理模型的边坡可靠度分析流程Fig.1 Flow chart of slope reliability analysis based on Subset simulation and the Kriging metamodel

（1）建立边坡稳定性分析模型：基于边坡几何参数和岩土体的物理力学参数建立边坡稳定性分析模型，可采用有限元法或极限平衡法进行建模。本文采用极限平衡分析软件SLOPE/W进行建模［24］。

（2）生成训练样本：基于土体参数统计特性，采用拉丁超立方抽样生成一定数量的训练样本。SILVESTRINI等［25］指 出 训 练 样 本 数 一 般 为10D～15D，其中D为随机变量个数［26］。

（3）计算样本响应值：将训练样本输入至步骤（1）边坡模型中，计算得到训练样本对应的边坡安全系数。

（4）构建训练样本数据集：将步骤（2）训练样本与步骤（3）计算得到的边坡安全系数进行组合，组成训练样本数据集。

（5）构建克里金代理模型：将训练样本数据集输入至克里金模型当中，计算模型中的未知参数，构建克里金模型。

（6）可靠度计算：基于步骤（5）建立的克里金代理模型，进行子集模拟，计算不同中间事件的条件概率，并利用公式（2）计算边坡失效概率。

3 算例

本节通过2个边坡算例说明所提出的方法的有效性。将直接蒙特卡洛模拟方法结果与本文方法结果进行对比，以验证本文所提方法对边坡可靠度计算的有效性。同时，探讨模型对训练样本数量和回归模型选择的敏感性。

3.1 算例I：单层粘性土质边坡

算例I为一单层粘性土质边坡，该边坡几何形状如图2所示，坡高为10 m，坡比为1∶1。土体重度γ=20 kN/m3，粘聚力c和摩擦角φ为服从对数正态分布的互相关随机变量，参数统计特征如表2所示。采用SLOPE/W模块中简化Bishop法进行极限平衡条分法边坡稳定性分析，模型共定义潜在滑面5985条。基于土体参数的均值，边坡的临界滑面如图2中所示，其安全系数为1.207，与文献中基本一致［11］。

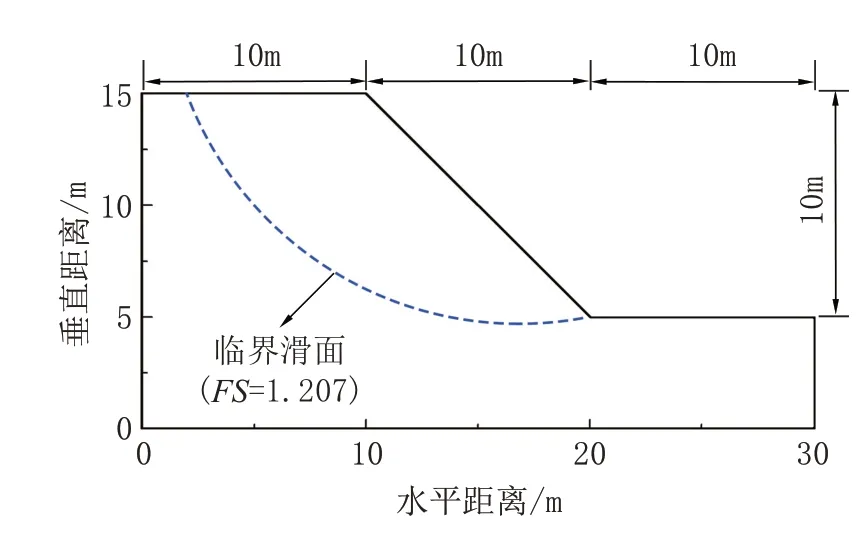
图2 算例I边坡几何结构与稳定性分析结果Fig.2 Slope geometry and slope stability analysis result for Example I

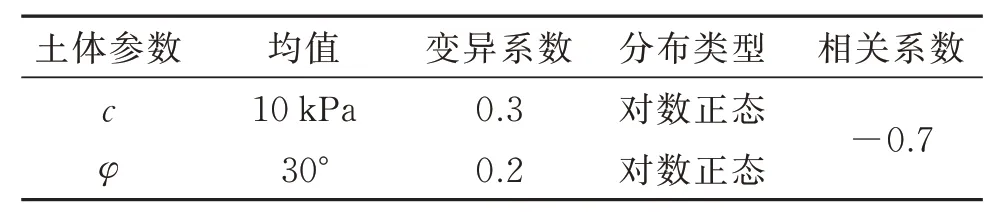
表2 算例I土体参数统计特性Table 2 Statistics of the soil parameters of Example I

在上述边坡确定性分析模型基础上，下面通过基于克里金的子集模拟法对该边坡开展可靠度分析。首先，根据10倍随机变量准则，利用拉丁超立方抽样技术生成20组标准正态随机样本，并将这些标准正态随机样本按照表2所示土体参数统计特性转换为对数正态随机样本，将其输入图2所示边坡稳定性分析模型，获得相应的边坡稳定性响应值，用于训练克里金模型。构建克里金代理模型时，回归模型选择二次多项式函数，相关函数模型选择高斯型。随后，将训练完毕的克里金代理模型接入子集模拟计算边坡失效概率，结果可得该边坡的失效概率为0.0530。

为验证本文方法的准确性与计算效率，将本文提出的方法与直接蒙特卡洛模拟、基于克里金的蒙特卡洛模拟的边坡可靠度计算结果进行对比，计算结果见表3。由表3可知，基于克里金模型的蒙特卡洛法与子集模拟方法均可对边坡失效概率开展高效分析，计算结果误差相较于蒙特卡洛模拟法均小于10%。同时，基于克里金模型的蒙特卡洛法与子集模拟方法计算时间相较于传统蒙特卡洛模拟法大幅度地降低。但需要指出的是，在基于克里金的蒙特卡洛模拟法中计算样本数设置为1×106，但若追求更高的计算精度，如当蒙特卡洛样本数达到或超过108时，模型内存占用将超出计算设备的内存容量（16 GB），从而导致内存溢出而无法进行计算。间接反应基于克里金的蒙特卡洛模拟在针对小概率失效事件的可靠度分析中存在一定的局限性。与之相比，基于克里金的子集模拟法在相近误差水平与计算时间的前提下，借助中间失效事件使得计算样本数仅1×103，大大降低了计算矩阵的维度，从而有效解决了基于克里金的蒙特卡洛模拟方法内存占用过大的问题。

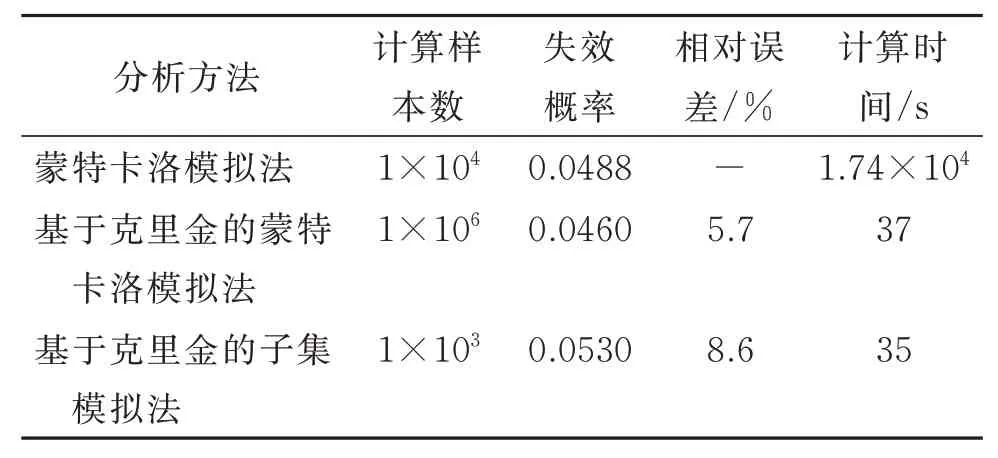
表3 不同分析方法计算的算例I边坡失效概率结果Table 3 Probability analysis results obtained by different methods for Example I

进一步地，为探究本文所提方法中训练样本数量对可靠度分析结果的影响，此处将不同训练样本数量下的计算结果与蒙特卡洛模拟结果进行对比。由图3可知，随着训练样本数量的增加，基于克里金的子集模拟的失效概率计算结果基本与蒙特卡洛模拟结果保持一致，同时计算结果的波动范围较小，说明采用10倍随机变量的样本数量已基本可满足该方法中训练模型精度需求。

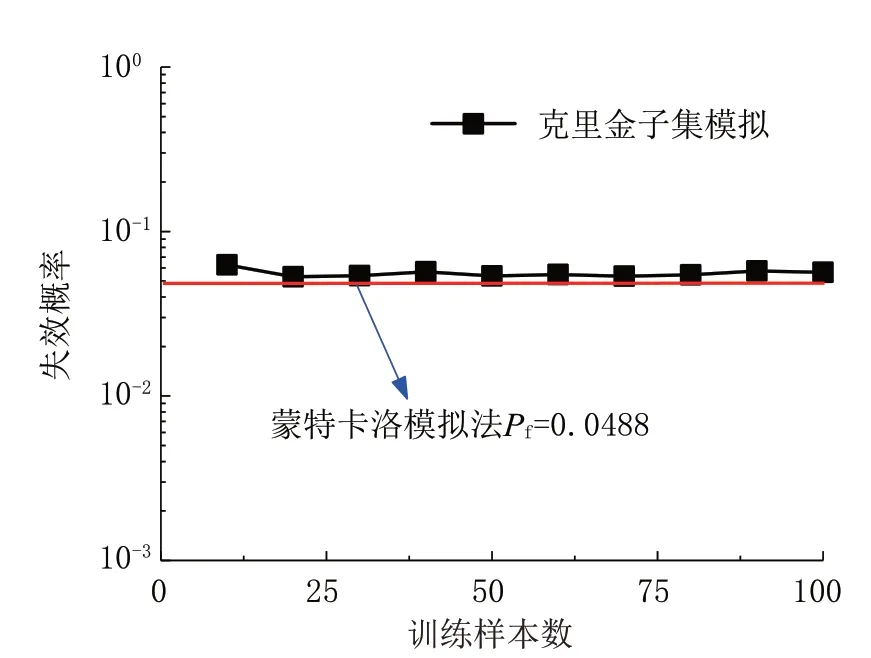
图3 算例I中失效概率与训练样本数关系Fig.3 Relationship between probability of failure and the number of training samples for Example I

为探究不同相关模型与回归模型对失效概率计算结果的影响，此处将不同模型的计算结果与蒙特卡洛模拟结果进行对比，计算结果更接近蒙特卡洛模拟则认为其计算精度更高。其中，训练样本数量均选择为20组。由表4可知，相较于常数型与一次函数回归模型，选取二次多项式的克里金模型对于失效概率的计算精度更高。在一次函数与二次多项式回归模型下的情况，不同相关模型对失效概率的计算结果影响较小。而在常数型回归模型下，高斯型与三次样条型相关模型的计算精度要显著高于其他3种相关模型。总的来说，上述结果表明二次型多项式回归模型与高斯型相关模型构建的克里金模型更适用于该边坡稳定性的失效概率计算。

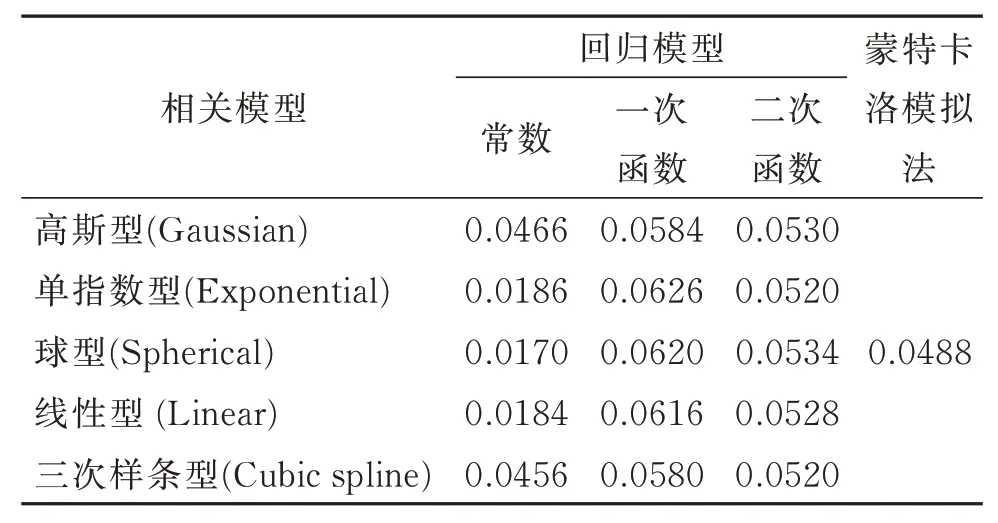
表4 算例I不同模型的边坡失效概率结果的比较Table 4 Probability analysis results obtained by different models for Example I

3.2 算例II：工程实例边坡

算例II为一工程实例边坡，该斜坡位于中国香港西贡区北部，由距坡顶9 m深的崩积层土体组成［27］。边坡根据不同倾角分为5个区段，边坡中部存有上覆物所致30 kN点荷载，地下水水位情况及相关工程地质情况如图4所示。土体重度γ=19 kN/m3，粘聚力c和摩擦角φ为服从对数正态分布的互相关随机变量，参数统计特征如表5所示。采用SLOPE/W模块中Morgenstern-Price法进行极限平衡条分法边坡稳定性分析，模型共定义潜在滑面5355条。基于土体参数的均值，边坡的临界滑面如图4中所示，其安全系数为1.330。

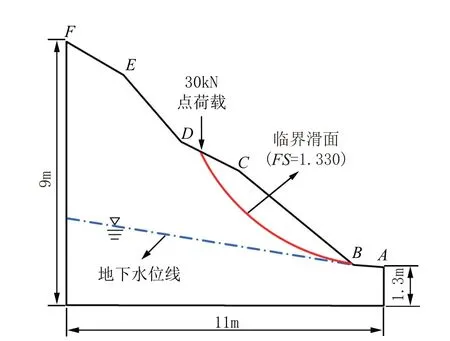
图4 算例II边坡几何结构与稳定性分析结果Fig.4 Slope geometry and slope stability analysis result for Example II

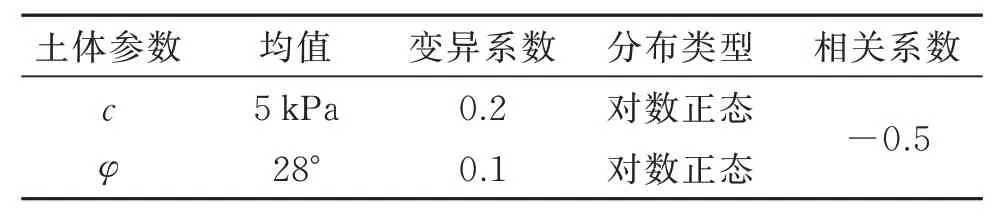
表5 算例II土体参数统计特性Table 5 Statistics of the soil parameters of Example II

通过基于克里金的子集模拟法对该边坡开展可靠度分析。首先通过拉丁超立方抽样生成一定数量（比如20）的训练样本，并输入至图5所示的边坡稳定性分析模型求解相应的安全系数值，进而组成一定数量的训练样本集，以此构建克里金代理模型。模型构建过程中，回归模型选择二次多项式函数，相关函数模型选择高斯型。然后，基于构建的克里金代理模型，开展子集模拟分析，计算得到该边坡的失效概率为0.0186。随后，将本文方法与直接蒙特卡洛模拟法以及基于克里金的蒙特卡洛法进行对比分析，结果如表6所示。由表6可得，基于克里金的子集模拟法在计算时间上大大低于蒙特卡洛模拟，同时计算精度也高于基于克里金的蒙特卡洛法。此外，在计算精度相近的情况下，基于克里金的子集模拟法（1×103）的计算样本数较基于克里金的蒙特卡洛法（1×106）降低了3个数量级，极大地降低了计算过程中计算资源的消耗，进一步证明了基于克里金的子集模拟法的计算效率更高。

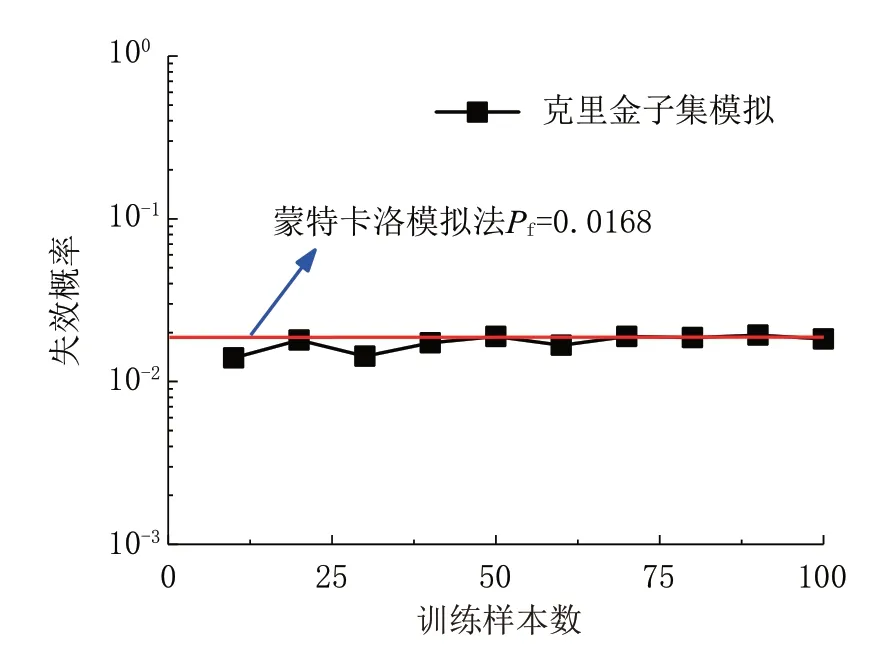
图5 算例II中失效概率与训练样本数关系Fig.5 Relationship between probability of failure and the number of training samples for Example II

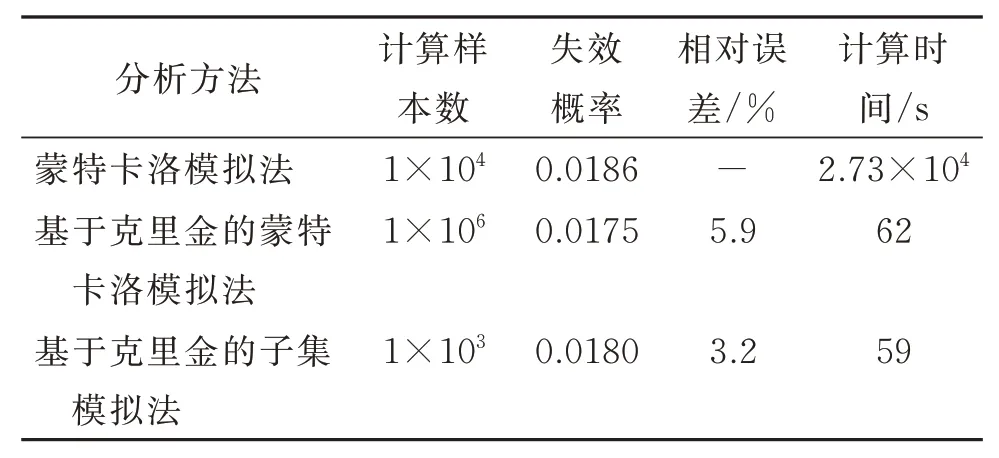
表6 不同分析方法计算的算例II边坡失效概率结果Table 6 Probability analysis results obtained by different methods for Example II

接下来，为了探究本文所提方法中训练样本数对可靠度分析结果的影响，此处将不同训练样本数量下的计算结果与蒙特卡洛模拟计算结果进行对比。由图5可知，随着训练样本数量的增加，基于克里金的子集模拟对于边坡失效概率围绕着蒙特卡洛模拟结果波动，但波动范围较小且基本与蒙特卡洛模拟法结果一致。与算例Ⅰ相同，采用10倍随机变量数的样本数量基本可满足该方法中构建模型的精度需求，并且随着训练样本的增加，边坡失效概率变化不显著。

4 结论

本文提出了一种基于克里金模型与子集模拟的边坡可靠度分析方法，并研究了不同回归模型和相关函数模型以及训练样本数对该方法精度的影响。该方法利用子集模拟估算边坡可靠度，可以有效用于高维小失效概率可靠度分析，提高边坡可靠度分析的计算效率与适用性。采用一个单层粘性土边坡与一个坚硬地层上的双层饱和不排水粘性土边坡验证了所提方法的有效性。得到的主要结论如下：

（1）基于克里金模型与子集模拟的边坡可靠度分析方法能够有效地替代传统蒙特卡洛模拟法，准确地估计边坡的失效概率。基于克里金的子集模拟法计算效率相较于传统蒙特卡洛方法显著提高。同时，该方法的计算精度可满足可靠度分析的需求。

（2）所提方法可有效解决边坡可靠度分析中的小概率失效事件。尤其在蒙特卡洛模拟法或耦合代理模型的蒙特卡洛模拟法中，过大的样本数可能造成计算内存占用过大甚至溢出，但子集模拟通过利用子集的概率乘积的方法可有效地降低计算矩阵维度，从而对小失效概率的边坡可靠度进行有效分析。

（3）构建克里金模型时，采用10倍随机变量数的训练样本即可得到满足计算精度需求的模型，而额外增加训练样本对计算结果影响较小。而回归模型与相关模型对克里金模型计算精度有着较大的影响。对比不同情形的计算结果与文献经验，本文建议采用二次型回归模型与高斯型相关模型进行边坡可靠度分析。