外骨骼膝关节构型设计与分析

崔心惠, 方 红, 朱山川

(1. 滁州职业技术学院 电气工程学院, 安徽 滁州 239000;2. 上海浦马机电工程技术有限公司, 上海 200333)

在工业生产过程中,人们常需保持半蹲姿势才能触碰到装配的工件所在的重要部位.长时间的半蹲姿势不仅加重膝关节的负担进而导致膝关节的退化,而且大大降低了工作的效率[1].

外骨骼在为穿戴者提供重力支撑时,其中膝关节的锁紧机构起着尤为重要的作用.即外骨骼的承重能力取决于膝关节锁紧机构的锁紧.同时,外骨骼膝关节还需满足不同转角的变化.文献[2]设计了一种棘轮棘爪锁紧机构,棘爪通过弹簧锁紧机构来保持与棘轮的接合和脱离从而实现关节的锁紧与松弛.文献[3-4]通过液压缸的伸缩来实现膝关节角度的调节,虽然液压缸能够提供较大载荷,但仍存在漏油以及不易调节的现象.文献[5-6]设计的机电控制方式可有效地实现膝关节的锁紧与放松,该方式控制精度高,易于调节,但体积较笨重且价格昂贵.文献[7]提出通过机械结构来实现膝关节的承重,具有结构简单,操作方便的特点,但只提供3个可使用位姿.

针对上述问题,本文提出一种新型的外骨骼膝关节构型,可用于膝关节任意转角的锁紧.

1 膝关节构型描述

1.1 膝关节运动分析

在设计膝关节外骨骼结构之前,需要对膝关节进行运动分析.膝关节是下肢中部关节,屈伸运动是其主要运动方式,此时膝关节可视为一种铰链式关节.如图1所示.

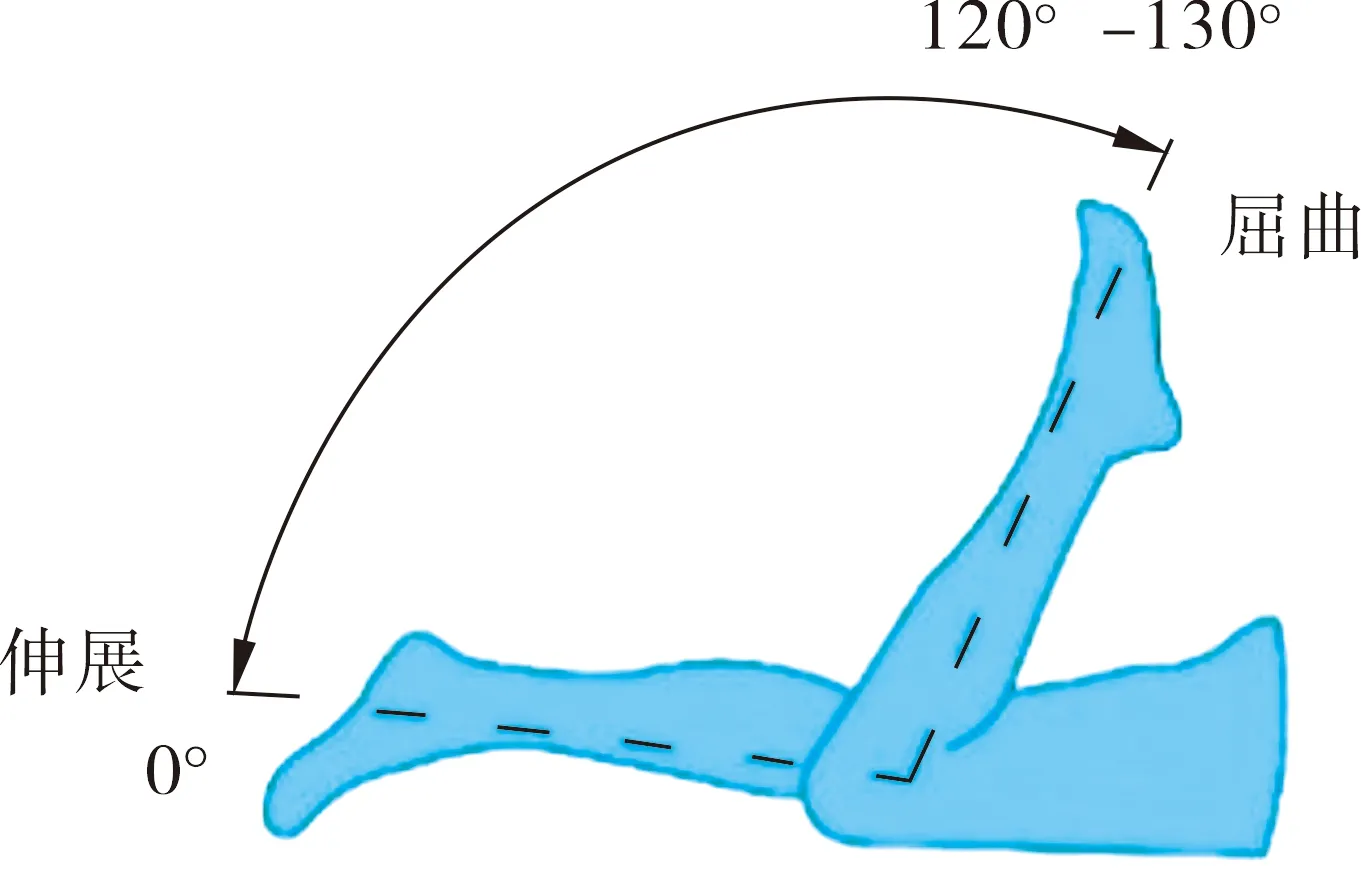
图1 膝关节的基本运动

1.2 关节设计

对于铰链关节来说,若仅含有1条支链,则应包含1个转动副,如图2(a)所示;若包含2条支链,那么为满足转动的需求,则应包含2个同轴的转动副如图2(b)所示;为保证该关节的刚度需求,本文所设计的关节采用并行支链结构.

(a)单支链 (b)并行支链 图2 铰链关节的支链形式

具体的关节设计步骤:

1) 求解机构约束螺旋系:关节具有1个转动自由度,通过机构的运动螺旋系,求解反螺旋得到关节机构的约束螺旋系为5系.

2) 分支链约束螺旋系:由机构的约束螺旋系可计算出分支的约束螺旋系,机构的约束螺旋系由2条并行支链提供,机构约束力为各支链的末端约束力的并集.右侧支链具有5个约束力,左侧分支的约束力不能超出该范围[8].

3) 右侧采用单转动副的固定约束支链,左侧采用多转动副的变约束力支链,以满足关节的使用需求.通过运动副的线性相关性来进行机构设计,左侧支链由3个空间平行力矢量和3个空间共点力矢量组成.通过改变左侧支链约束力来实现关节的转动与有效锁紧.

1.3 关节结构介绍

关节模型由上、下平台和2条支链共同组成,其中左支链由按顺序连接的6个转动副以及连杆组成.右支链由1个转动副以及连杆组成,左右两支链均有1个主动运动副,其余均为被动副,具体结构如图3所示.

1—上平台;2—左支链;3—下平台;4—主动转动副;5—右支链图3 关节结构

1.4 锁紧条件

锁紧的方式如图4所示.此处用Ri表示第i个转动副,在初始位姿时R1、R3和R63个转动副的轴线空间汇交于一点,且位于R7轴线的延长线上,左右2条支链等同于同轴转动,此时关节可动.在主动转动副R2驱动时,自然会改变转动副R3的轴线位置,此时轴线汇交的R1、R3和R6轴线不再汇交,故左右两支链不再同轴,由于约束力的变化和主动力做功的改变,关节可实现任意角度的锁紧.

图4 关节锁紧原理

2 机构的运动分析

2.1 可动性分析

为了简化问题,建立如图5所示的坐标系,其中坐标原点o为R1、R3和R6轴线的汇交点,x轴沿着R3轴线方向,y轴沿着R7轴线方向,z轴遵循右手定则.

图5 机构坐标系

假设R1、R3和R6转动副的轴线空间汇交时为姿态1,当R1、R3和R6转动副的轴线空间不再汇交时为姿态2.在姿态1时,左支链的运动螺旋系可表示为

(1)

动平台的速度为

(2)

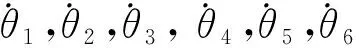
$p=0.

(3)

机构可动的充要条件是其支链上的所有旋量线性相关[10],其中R2可由R1、R3、R4、R5、R6线性表示.左支链的运动不会引起动平台的运动.由式(1)可知,左支链的运动螺旋系为5系,该分支对动平台的运动提供一个约束螺旋为

$ro=(0, 1, 0, 0, 0, 0).

(4)

式(4)表明,左支链的约束螺旋系仅包含沿y轴方向的约束力,该支链限制动平台沿y轴移动的自由度.右支链提供固定约束,运动螺旋系表示为

$7=(0, 1, 0, 0, 0, 0).

(5)

右支链的运动螺旋系为1系,那么约束螺旋系为5系,由互易积理论有

(6)

由式(6)可知,右支链的约束螺旋系包含3个轴线互相垂直的约束力和2个分别垂直于xoy面和yoz面的约束力偶,即该分支链约束了动平台空间内的3个移动自由度和2个垂直于xoy面和yoz面的转动自由度.并联机构的自由度可利用修正Grubler-Kutzbach公式进行计算[11]，即

(7)

式中:M为机构自由度数;λ为机构阶数;n为机构的构件总数;g为机构运动副总数;fi为第i个运动副的自由度数;μ为冗余约束数;ξ为局部自由度数.

M=6(7-7-1)+7+0=1.

(8)

此时,M=1表明人体膝关节自由度为1,达到膝关节一个方向的转动,满足实际应用需求.

动平台的约束为2条支链的交集,在姿态1时,机构的动平台仅含有1个沿y轴转动的自由度.姿态2,即在R2的驱动后,R3的轴线发生变化,此时R1、R3和R6的轴线不再汇交.R3对应的运动螺旋可表示为

$3=(x3,y3,z3,a,b,c).

(9)

此时,提供固定约束的R7与R1,R3,R4,R5,R6线性无关,左侧支链不参与运动,故当R2和R7同时驱动时,即R3转动副的轴线发生变化,此时关节不满足转动要求,可进行关节的锁紧.

2.2 ADAMS仿真

为了更好地分析关节运动的实际过程,上下关节均简化为相同的圆柱体并利用转动副将各连杆进行连接.在此过程中,各连杆所处位置及相互之间的几何关系均符合上文表述.R2和R7主动副分别对应驱动函数为STEP(time, 0, 0 d, 2, 0 d)-STEP(time, 2, 0 d, 3, 30 d)和30.0 d * time.通过ADAMS建立仿真模型,如图6所示.

图6 ADAMS仿真模型

在位姿1,此时仅有R7主动副驱动.此处关节存在一个绕y轴方向的转动自由度,则可直接对上关节在x轴方向的运动进行分析.分别测量了质心点在x轴方向的运动变化曲线,如图7所示.

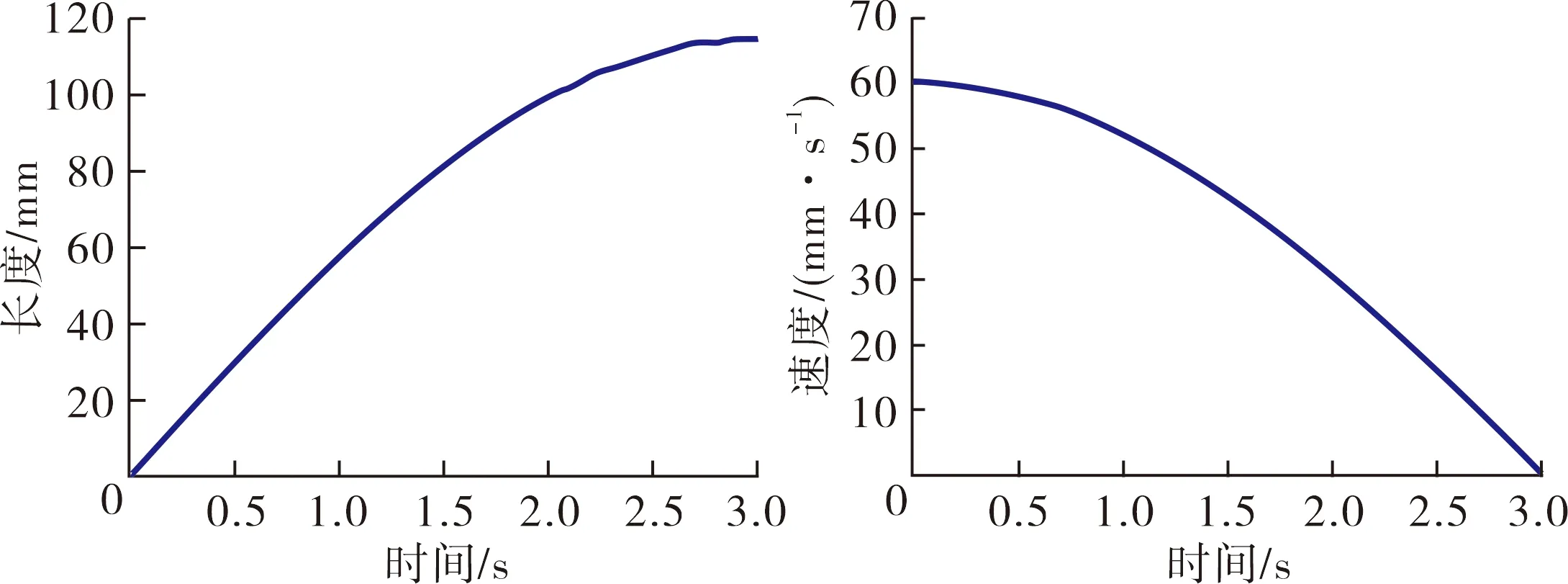
(a) 位移曲线 (b) 速度曲线图7 R7驱动时质心点在x轴方向的运动变化曲线

在0～2 s,即R2和R7主动副共同驱动,第三转动副的轴线并未发生变化.一旦超过2 s第三转动副的轴线开始改变.上关节质心点在0～3 s内的运动变化曲线如图8所示.

(a) 位移曲线 (b) 速度曲线图8 R2和R7驱动时质心点在x轴方向的运动变化曲线

从运动变化曲线中可看出,当只存在R7驱动时,整个关节可在一定时间范围内发生转动.当R2和R7进行共同驱动时,仿真结果会在2 s后结束.

其实质是主动副R2在2 s内并未发挥作用,而实际发生转动变化是由R7主动副决定;R2主动副一旦驱动,R3的轴线立即随之发生变化,此时关节出现从位姿1转变到位姿2的现象,在此过程中机构不可动且仿真结束.ADAMS运动学仿真符合上文中的理论分析,表明该关节可有效实现相邻关节之间的锁紧.

3 静刚度建模

3.1 刚度矩阵的推导

施加在上平台中心点的外力(或力矩)相当于3种力Fx,Fy,Fz和3个转矩Mx,My,Mz的组合,矩阵的形式可表示为[12]

t=[FM]T=[FxFyFzMxMy,Mz]T.

(10)

上平台的位移和虚位移为

q=[xyzαβγ]T,

(11)

δq=[δxδyδzδαδβδγ]T.

(12)

由文献[10],每个分支中均提供1个主动力,由虚功原理可以推导出

tTδq=taTδqa+tcTδqc,

(13)

式中:ta为驱动器的驱动力;tc为分支中的约束力;δqa为驱动力传递到上平台所引起的虚位移;δqc为约束力传递到上平台所引起的虚位移.

δqa=Jaδq,

(14)

δqc=Jcδq,

(15)

式中:Ja为驱动力雅可比矩阵;Jc为约束力雅可比矩阵.

tTδq=taTJaδq+tcTJcδq,

(16)

将式(16)化简为

t=JaTta+JcTtc.

(17)

在小变形下,设关节的力和变形关系满足胡克定律,则有

2.5 疼痛护理 观察疼痛性质、持续时间。教会患者根据“长海痛尺”进行自我疼痛评分，小于4分时给予心理安慰和分散注意力，大于4分遵医嘱适当给止痛药，效果较好［3］。

(18)

式中:k为整个关节的整体刚度矩阵；ka和kc分别为驱动力和约束力的刚度矩阵,ka=diag[ka1ka2]，kc=diag[kc1kc2] ；kai和kci(i=1,2)分别是第i条分支链的驱动力刚度和约束力刚度.

kδq=JaTkaδqa+JcTkcδqc.

(19)

把(14)和(15)带入式(19)中化简后可得

k=JaTkaJa+JcTkcJc.

(20)

3.2 全雅克比矩阵的求解

3.2.1 约束雅克比矩阵

用l02,l04,l05表示第二,第四、第五转动副轴线相对于坐标系原点的矢径,第一支链均为单自由度运动副.上平台的速度可表示为

(21)

(22)

式中：

对于第一分支链,与所有第一分支链的螺旋相对应的约束螺旋可以表示为

(23)

由旋量理论可知,运动螺旋$m与约束螺旋$r1存在下式:

$m·$r1=0,

(24)

其中·表示2个旋量的互易积,上式可表示为

Jc1$m=0.

(25)

求得第二分支链的约束螺旋系Jc2,则整个关节的约束雅克比矩阵Jc可写为

(26)

3.2.2 驱动雅克比矩阵

如果锁定主动关节,在每一个分支链中都增加一个新的反螺旋[13],可以表示为

(27)

将式(21)与时(22)同时与$ai求互易积,结果可表示为

(28)

(29)

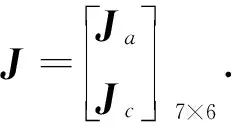
(30)

4 刚度分析

关节的结构参数如表1所示,其中aij为第i个转动副与第j个转动副之间连杆的长度.r为上、下关节的半径,h为上、下关节之间的高度.如果将各支链位移最小的位置作为初始位置,可以计算出关节在初始姿态的全刚度矩阵,如式(31)所示.

表1 关节的结构参数 mm

K=107×

(31)

其中k11、k22和k333项的单位是N/m;k44、k55和k663项的单位是N·m/rad.

根据各零部件刚度,由解析模型可求得坐标系下的下平台在其工作空间的平面各向刚度的分布情况.kx、ky、kz分别表示沿x、y、z轴的线刚度；kax、kay、kaz分别表示沿x、y、z轴的角刚度.

从图9中可看出:x、z轴的线刚度均呈现两侧对称分布,当z为一定值时,刚度会随着x、y位移量的增大而逐渐增大.kx、kz明显大于ky,同时kx、kz和kax、kaz也存在明显的相似变化趋势并且变化不大.而ky、kay具有相反的变化趋势.图10中可以看出关节上平台在z=0.1 m平面的最大、最小刚度特征值均是呈对称分布.

(a) x向线刚度 (b) y向线刚度

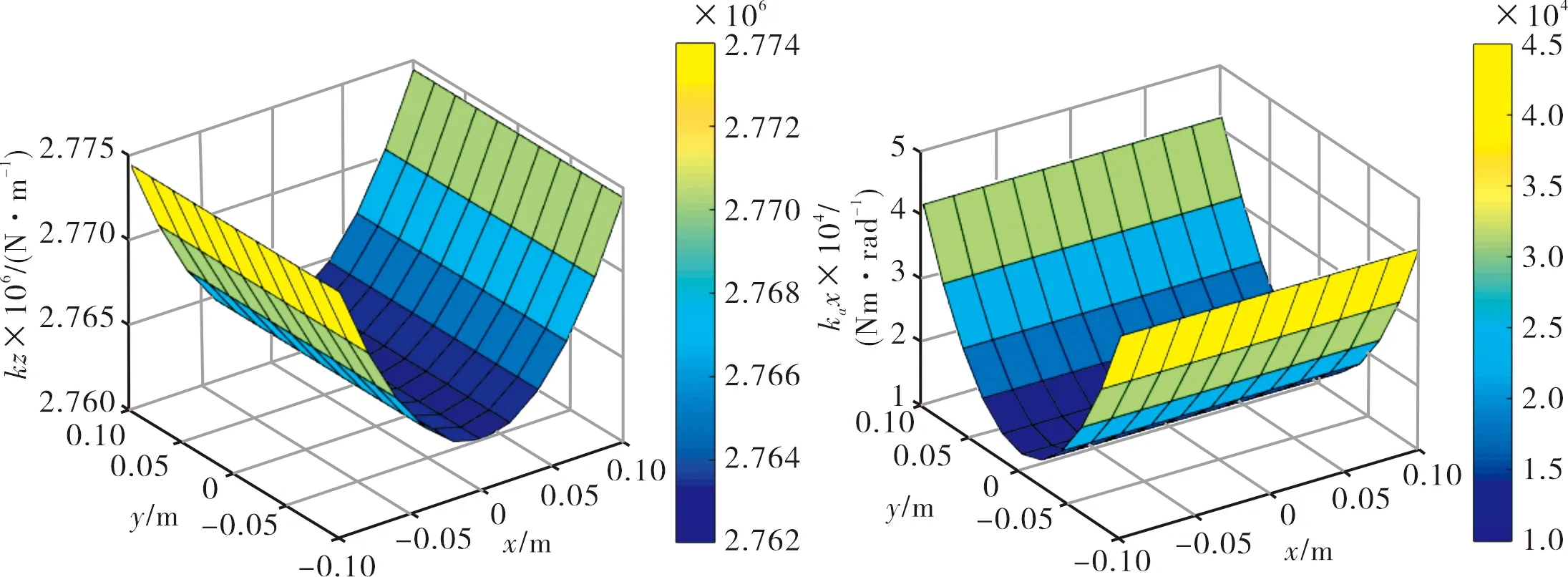
(c) z向线刚度 (d) x向角刚度

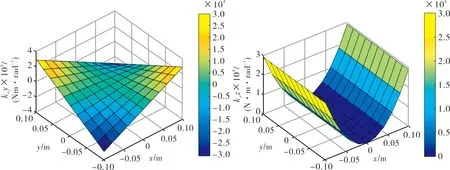
(e) y向角刚度 (f) z向角刚度图9 在工作区的x、y横截面上的刚度曲线

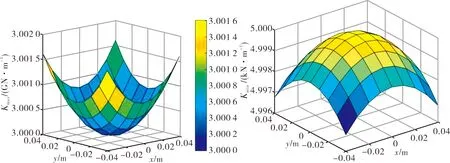
(a) 最大刚度 (b) 最小刚度图10 在工作区的x、y横截面的最大及最小刚度特征值分布图

5 结语

针对外骨骼膝关节承重问题,通过对膝关节运动形式进行分析,进而提出一种新型的外骨骼膝关节.采用旋量理论对所提出新型外骨骼膝关节进行可动性分析,在建立雅可比矩阵的基础上,利用虚功原理对关节的全刚度矩阵及刚度模型进行推导.结果表明,机构在静载荷下的变形情况具有一定的空间变形规律,与此同时关节的刚度性能指标呈对称分布,实现了膝关节在不同转角下的锁紧,具有一定的理论参考价值.