“双碳”背景下线间潮流控制器多目标协调控制策略

蔡 晖， 高伯阳， 祁万春， 吴 熙， 谢珍建， 黄俊辉

(1. 国网江苏省电力有限公司经济技术研究院，南京 210008；2. 东南大学 电气工程学院，南京 210096)

符号说明

A、B、C、D—系统状态矩阵

Cdc—直流电容

D—同步电机定常阻尼系数

Efd—同步电机励磁电动势

Eq—同步电机空载电动势

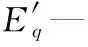
G1(s)、G2(s)—电力系统传递函数

H—机组惯性时间常数

Id、Iq—线路d轴电流、q轴电流

Iij、Iik—线路ij、ik间的电流

Iijd、Iijq—线路ij间电流的d轴分量、q轴分量

Iikd、Iikq—线路ik间电流的d轴分量、q轴分量

Iild、Iilq—线路il间电流的d轴分量、q轴分量

k—常规控制增益

K—放大环节增益

Ka—同步电机自动电压调节器增益

K1、K2、Kpd、Kpm1、Kpθ1、Kpm2、Kpθ2、K3、K4、Kqd、Kqm1、Kqθ1、Kqm2、Kqθ2、K5、K6、Kpd2、Kvd、Kpm3、Kpθ3、Kpm4、Kpθ4、K7、K8、K9、Kcm1、Kcθ1、Kcm2、Kcθ2、Kjp1、Kjp2、Kjp3、Kjpm1、Kjpθ1、Kjpm2、Kjpθ2、Kjq1、Kjq2、Kjq3、Kjqm1、Kjqθ1、Kjqm2、Kjqθ2、Kkp1、Kkp2、Kkp3、Kkpm1、Kkpθ1、Kkpm2、Kkpθ2—与系统参数和初始运行条件有关的常数

m1、m2—主控侧、辅控侧换流器调制比

M—惯性常数

Pe—同步电机输出瞬时功率

Pij—主控侧实时有功功率

Pijref—主控侧有功功率参考值

Pik—辅控侧实时有功功率

Pikref—辅控侧有功功率参考值

Pm—同步电机机械功率

Pn—发电机输出有功功率

Qij—主控侧实时无功功率

Qik—线路ik输送的无功功率

Qijref—主控侧无功功率参考值

T1、T2、T3、T4—超前滞后补偿环节时间常数

Ta—同步电机自动电压调节器时间常数

Tw—隔直环节时间常数

u—常规控制输出信号

u1、u2—闭环控制输入信号

Vdc—直流电容实时电压

Vdcref—直流电容电压参考值

VT—同步电机端电压

VT0—同步电机端电压参考值

Vi、Vj、Vk、Vl—节点i、j、k、l电压

VTd、VTq—同步电机端电压d轴分量、q轴分量

Vjd、Vjq—节点j电压d轴分量、q轴分量

Vkd、Vkq—节点k电压d轴分量、q轴分量

Vseij、Vseik—线路ij、ik上的换流器电压

Vseijq、Vseijd—主控侧等效电压源q轴分量、d轴分量

Vseikq、Vseikd—辅控侧等效电压源q轴分量、d轴分量

X11d、X21d、Xjd、Xe1d、X12d、X22d、Xkd、Xe2d、X13d、X23d、Xld、Xe3d、X11q、X21q、Xjq、X12q、X22q、Xkq、X13q、X23q、Xlq—与线路和发电机参数有关的阻抗值

Xd、Xq—定子d轴电抗、q轴电抗

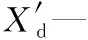
y1、y2—电力系统输出信号

θ1、θ2—主控侧、辅控侧换流器电压相角

δ—同步电机转子角

ω—转子角速度

ω0—基准角频率

在“碳达峰、碳中和”目标提出的背景下，新能源的战略地位进一步明确，清洁能源将迎来更加持续、高速的发展，我国电力系统深度脱碳已成为必经之路.这种能源转型为电网带来了强不确定性和低惯性等特征，对清洁能源的传输消纳与系统的安全稳定运行提出了新的挑战.

一方面，在“双碳”背景下，高比例清洁能源发电与并网技术不断发展，大规模水、风、光等清洁能源持续接入电网，各地新能源的开发力度逐渐加大，局部地区负荷密度迅速增长，恶化了潮流分布不均的情况，这不仅制约了交流输电系统的潮流输送能力，还增加了电网低碳运行的控制难度，使电力系统的柔性调节需求不断增强.

另一方面，考虑到新能源接入后的可控性相对较差，高比例新能源电力系统除了会引发能源传输消纳上的难题，还会在电网安全运行上带来挑战.作为世界上清洁能源并网规模最大的国家，我国有着复杂的地型和多样类型的气候，新能源日内最大功率波动较大.据相关资料[1]介绍，风电日波动最大幅度可达装机容量的80%，而光伏发电受昼夜变化、天气变化、移动云层的影响，同样存在间歇性和波动性.同时，高占比可再生能源电网存在惯性降低的问题，频率将更加不稳定，功角稳定特性将更加复杂，随机性波动现象将更加严重，给电力系统的低碳高效运行带来了安全隐患.

为了增强“碳达峰、碳中和”背景下电网的柔性调节能力、抗扰动能力和支撑新能源发展能力，需要有效手段来解决上述问题.综合型柔性交流输电系统(FACTS)设备在提高电网安全运行水平、优化已有资源配置等方面取得了较好的应用成果[2-4]，有利于建设适应高比例新能源广泛接入的新型电力系统.近年来，统一潮流控制器(UPFC)在我国得以应用[5]，大幅提升了所在电网的输电能力，但由于自身的拓扑限制，UPFC一般只能控制单输电通道潮流，无法同时对多输电通道潮流进行均衡，且UPFC所控过载部分潮流将通过自然分布的形式散布至其他输电通道，有可能使得其他邻近重载线路潮流越限.

线间潮流控制器同为第三代FACTS设备的典型代表[6-9]，能够大幅度提升电网输电能力与柔性控制水平，增加电网输电线路利用率和系统运行效率，从而节约廊道资源与新建通道投资[10].相较于 UPFC[11]，线间潮流控制器(IPFC)不仅能灵活、准确地调控不同输电通道的潮流，而且可以避免其他临近重载的线路出现潮流越限的情况[12-13].此外，这种新型装置能根据电力系统的运行状态，实时进行暂态稳定控制及阻尼振荡控制.因此，IPFC在负荷密集型的电力系统中有着广阔的应用前景[14-15].

然而，IPFC控制各目标的原理并不相同，被控量间也存在着交互影响与矛盾关系，控制目标会因为彼此间的针对性调节而产生波动.进一步地，IPFC在不同系统工况下也有着不同的主要关注对象，例如在稳态时着重优化线路潮流分布，受到暂态扰动的过程中则着重于抑制系统振荡[16].综上所述，作为一种建设成本较高的装置，IPFC应当考虑不同运行场景，兼顾各种系统约束条件，协调目标间的控制.为此，应当分析目标间的相互影响关系，加强IPFC潮流追踪，提高暂态稳定和小干扰稳定等多个要求，从而为IPFC适应不同运行工况、走向工程实用化提供一定的技术支撑.

鉴于此，提出了一种线间潮流控制器交互影响分析方法及多目标协调控制策略.基于改进相对增益矩阵(MRGA)理论对含IPFC的系统状态方程进行了线性化，量化了目标间的交互影响，定量分析了IPFC控制目标间的相互作用和排斥关系，选择了附加控制器的叠加位置，削弱了稳态调控与动态控制间的交互影响.进一步地，针对暂态过程，设计了多目标模糊逻辑控制器及基于模糊自适应控制的协调策略.结合粒子群算法优化了IPFC模糊控制器参数，在提高了暂态稳定和小干扰稳定的同时，减少了暂态过程中的潮流超调，挖掘了IPFC在不同系统运行工况下的协调控制潜力，有利于电力系统低碳运行的安全性与稳定性.

1 IPFC工作原理

IPFC是一种针对多条线路潮流控制功能更为强大的综合型FACTS装置，由多个共用直流母线的电压源换流器组成，通过串联耦合变压器接入不同的输电线路，灵活、准确地调控各通道潮流.

图1所示为IPFC的通用结构示意，其中VSC为换流器，n为换流器串联线路编号.各换流器通过换流变压器接入系统，在运行调控时对所处线路注入幅值和相角均可控的等效注入电压.

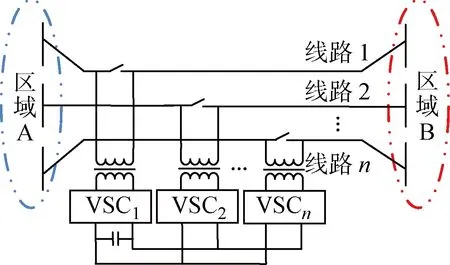
图1 IPFC结构示意图Fig.1 Schematic diagram of IPFC

可以选择一条或数条传输线路作为主控线路，并选择剩余的线路作为辅控线路，在确保主控线路潮流不越限的情况下，将过载潮流合理分配至其他线路.类似于其他的FACTS设备，IPFC本身相对于整个系统而言，在运行的过程中并不会对外部输送有功功率，也不会从外部吸收有功功率，这意味着各换流器间的有功交换始保持着动态平衡的状态.

IPFC动态模型控制框图如图2所示.主要包括主控侧有功、主控侧无功、辅控侧有功和直流侧电压4个比例积分(PI)控制器和Vdc计算模块.4个PI控制器的输入分别为主控侧有功功率参考值Pijref与主控侧实时有功功率Pij；主控侧无功功率参考值Qijref与主控侧实时无功功率Qij；辅控侧有功功率参考值Pikref与辅控侧实时有功功率Pik；直流电容电压参考值Vdcref与直流电容实时电压Vdc.PI控制器的输出分别为主控侧等效电压源q轴分量Vseijq、d轴分量Vseijd；辅控侧等效电压源q轴分量Vseikq、d轴分量Vseikd.

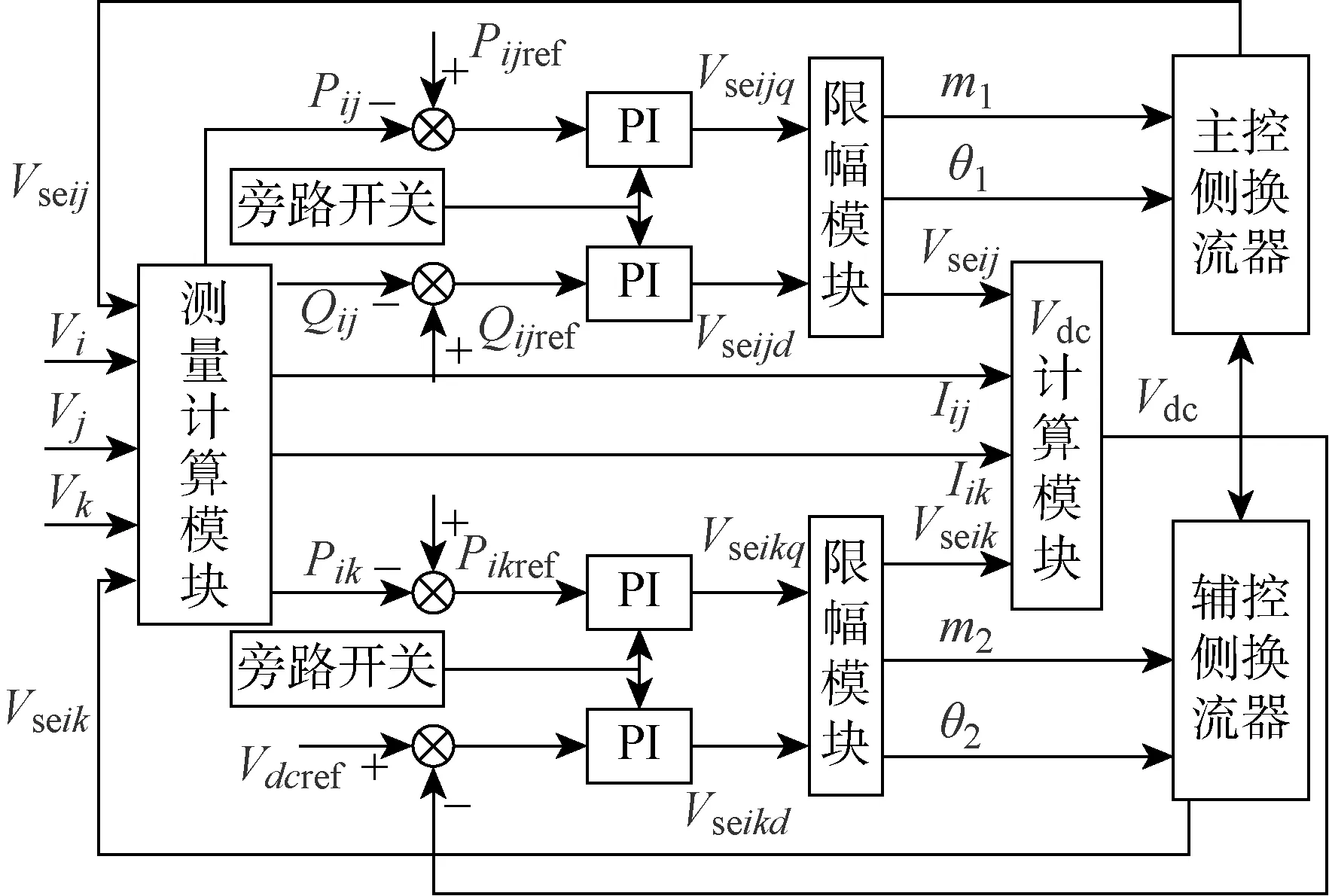
图2 IPFC动态模型控制框图Fig.2 Control diagram of IPFC dynamic model

换流器在运行调控的过程中，需保持主、辅控线路间的有功交换平衡约束.IPFC通过改变θ2平衡换流器间的有功动态交换，实现直流侧的稳压.动态模型中的直流电容充放电过程用下式反映：

(1)

式中：t为时间.

2 IPFC控制目标交互影响分析

2.1 改进相对增益矩阵(RGA)算法

为了削弱IPFC稳态调控与动态控制间的交互影响，通过MRGA理论量化分析IPFC各控制器的控制目标交互影响，选择附加控制器的叠加位置，如图3所示.

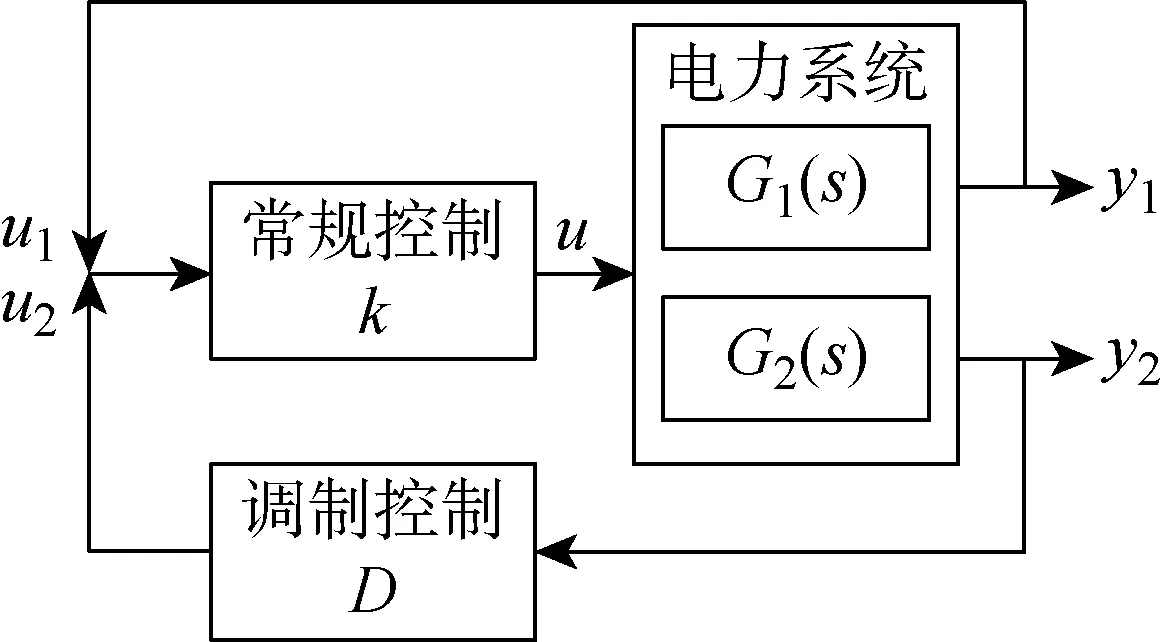
图3 控制目标的叠加示意图Fig.3 Schematic diagram for superposition of control targets

作为一种定量分析交互影响的有效方法，相对增益矩阵(RGA)理论常被用来寻找目标间的最小静态交互影响，并选择最佳控制变量配对.考虑到IPFC附加控制被叠加在常规控制上，此时若仍采用传统RGA计算，则会因式中系统传递函数G(s)矩阵稳态时的值G(0)为奇异矩阵而无法得到结果[17-18].鉴于此，基于RGA的基本原理引出MRGA理论.

根据RGA基本思想可知，输入u1对输出y2的交互影响为

(2)

式中：C1表示所有控制开环回路；C2表示y1-u1闭环回路.

同样，输入u2对输出y1的交互影响为

(3)

式中：C3表示y2-u2闭环回路.

根据相关推导有：

(4)

λ12与λ21即为求得的相对增益，可量化目标间的交互影响.若二者在数值上越接近1，则说明此时评估的通道间交互影响较小.反之，若二者取值较大，则表明此时评估的通道间交互影响很大[17].

定义好评估体系后，按以下步骤量化控制目标间的交互影响：

(1) 结合需要研究的电力系统，建立含IPFC控制器的状态方程，对模型线性化并转化为传递函数形式G(s).

采用Phillips-Heffron线性化模型[18]，将装有IPFC的系统表示为下式所示的状态空间方程形式：

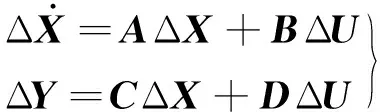
(5)

转化为频域传递函数的形式有：

(6)

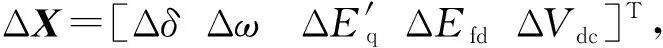
(2) 依次量化分析附加控制信号的各种选择方案.取s=0，得到系统稳态增益矩阵，并结合式(4)得出每种方案下λ12与λ21的计算结果.

(3) 结合MRGA的物理意义，分析不同控制方式下控制目标间的交互影响大小，选择相对增益最接近l的最佳控制配对.

2.2 装有IPFC电力系统的Phillips-Heffron模型

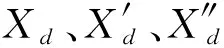
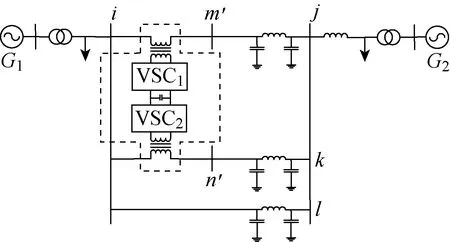
图4 IPFC安装场景Fig.4 Installation scene of IPFC

表1 发电机主要参数Tab.1 Main parameters of generator

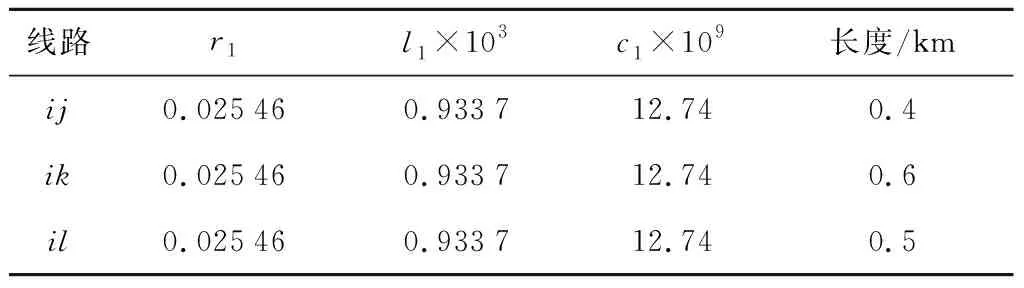
表2 线路主要参数Tab.2 Main parameters of line

首先线性化含IPFC控制器的状态方程模型，从而得到电力系统的传递函数模型G(s).系统采用一阶励磁系统模型，其动态模型为[18]

(7)

(8)

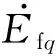
根据相关文献和推导可得所需研究的系统中机端电流方程为[19]

(9)

式中：

(10)

(11)

将式(9)～式(11)代入式(8)并线性化，可得：

(12)

进一步地，将式(12)代入式(7)并线性化，有：

(13)

将式(9)～式(11)代入式(1)并线性化可知：

Kcθ1Δθ1+Kcm2Δm2+Kcθ2Δθ2

(14)

由图4可知：

(15)

即可得到：

(16)

将式(16)代入式(14)～式(15)并线性化：

(17)

综合式(13)、式(14)和式(17)，可得式(5)中各矩阵A、B、C、D分别为

A=

(18)

B=

(19)

(20)

(21)

2.3 基于MRGA的控制目标交互影响分析

在量化交互影响的过程中，为了能更清楚地揭示交互影响的实质，取主控有功控制器m1=Kp1(Pijref-Pij)，主控无功控制器θ1=Kq1(Qijref-Qij)，辅控有功控制器m2=Kp2(Pikref-Pik)，直流电压控制器θ2=Kdc(Vdcref-Vdc)，其中Kp1、Kq1、Kp2、Kdc分别为线路ij有功功率、线路ij无功功率、线路ik有功功率及直流电压PI控制器比例系数.分别线性化后代入式(4)，得到调制控制附加于IPFC不同控制回路时的MRGA，具体计算结果如表3所示.

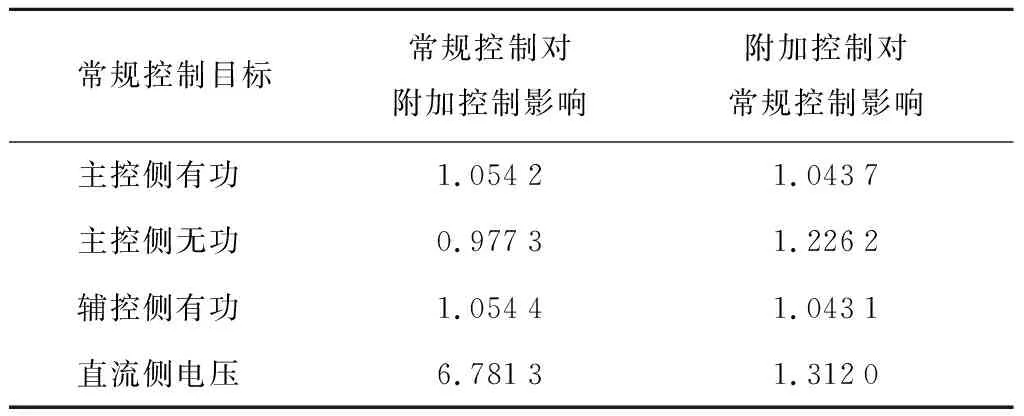
表3 IPFC交互影响的MRGA计算结果Tab.3 MRGA calculation results of interaction of IPFC

可知，当附加控制叠加于有功功率控制和无功功率控制时，该回路与各常规回路彼此间的影响相对较小；而叠加于直流电压的附加控制也没有对常规控制造成很大影响，但直流电压控制却与附加控制产生了比较明显的交互作用.为了提高IPFC协调控制的效果，不应将附加控制直接叠加于直流电压控制上.

以类电力系统静态稳定器(PSS)线性阻尼控制器作为附加控制器，验证直流侧电压控制与调制控制的交互影响.线性调制控制器设置参数设置为K=35，T1=0.2，T2=0.05，T3=0.3，T4=1.控制框图如图5所示.其中，阻尼控制器的输出信号与Pij和Pijref叠加在一起作为有功PI控制器的输入.在IPFC附近发电机中随机加入大小不等的扰动源，如图6所示.

图5 类PSS线性阻尼控制器Fig.5 Similar PSS linear damping controller

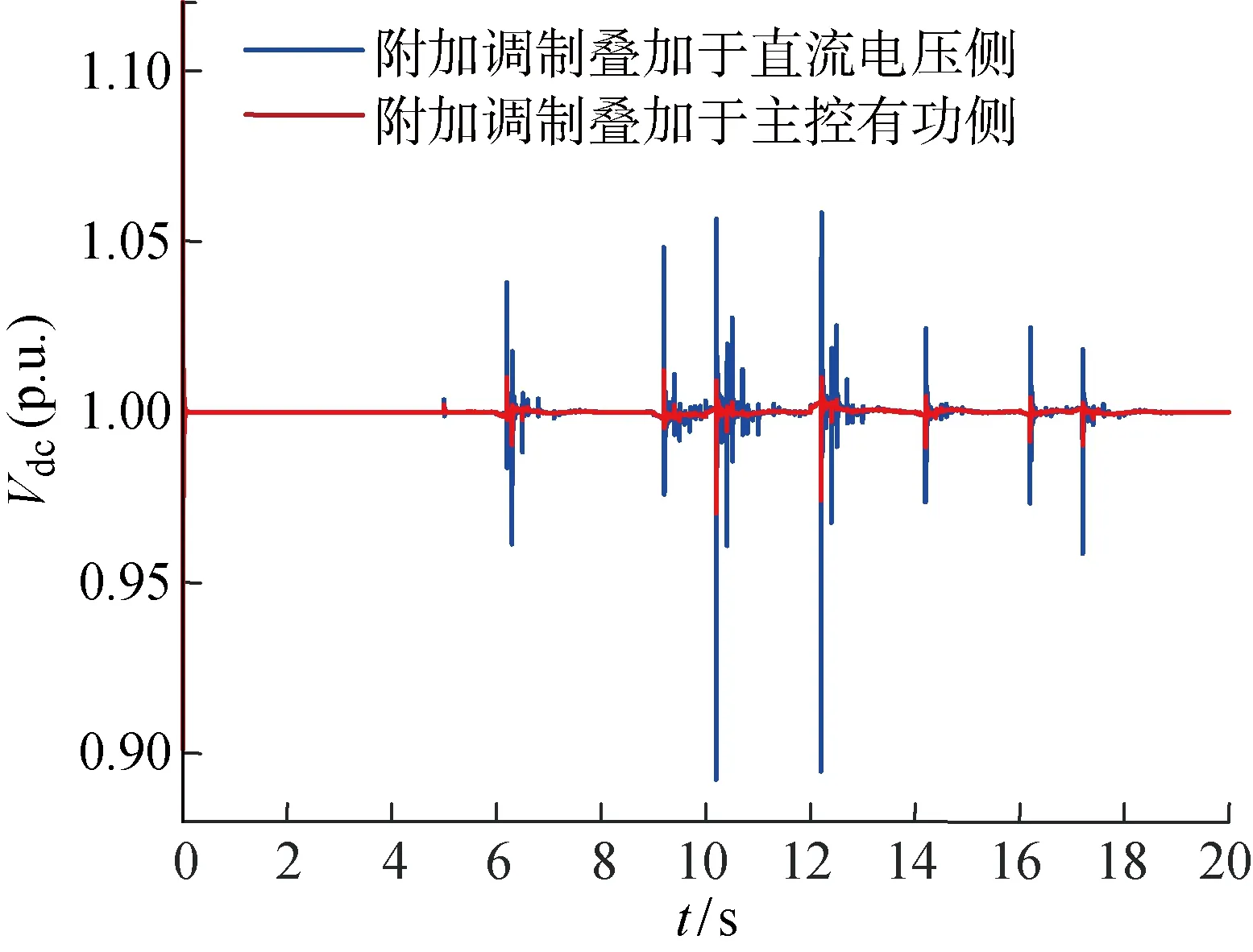
图6 交互影响验证Fig.6 Verification of interaction effect

从二者的对比可以看出，当附加控制叠加于有功侧时，直流电容电压波动范围更小，持续时间更短，与上述通过MRGA计算得出的结论相符.因此，将附加控制器叠加于Pij与Pik上，避免附加控制器在动态控制时与其他控制器之间的交互作用影响到各回路间的协调运作，从而削弱稳态调控与动态控制间的交互影响.

3 基于模糊逻辑的IPFC暂态协调控制

在削弱了IPFC稳态调控与动态控制间的交互影响之后，设计IPFC多目标协调控制策略，在提高暂态稳定和小干扰稳定的同时，减少暂态过程中的潮流超调.考虑到线性附加控制器的参数是基于系统某一运行点的线性化设计的，对系统工况变化的适应性差[20]，可基于模糊逻辑设计IPFC协调控制.

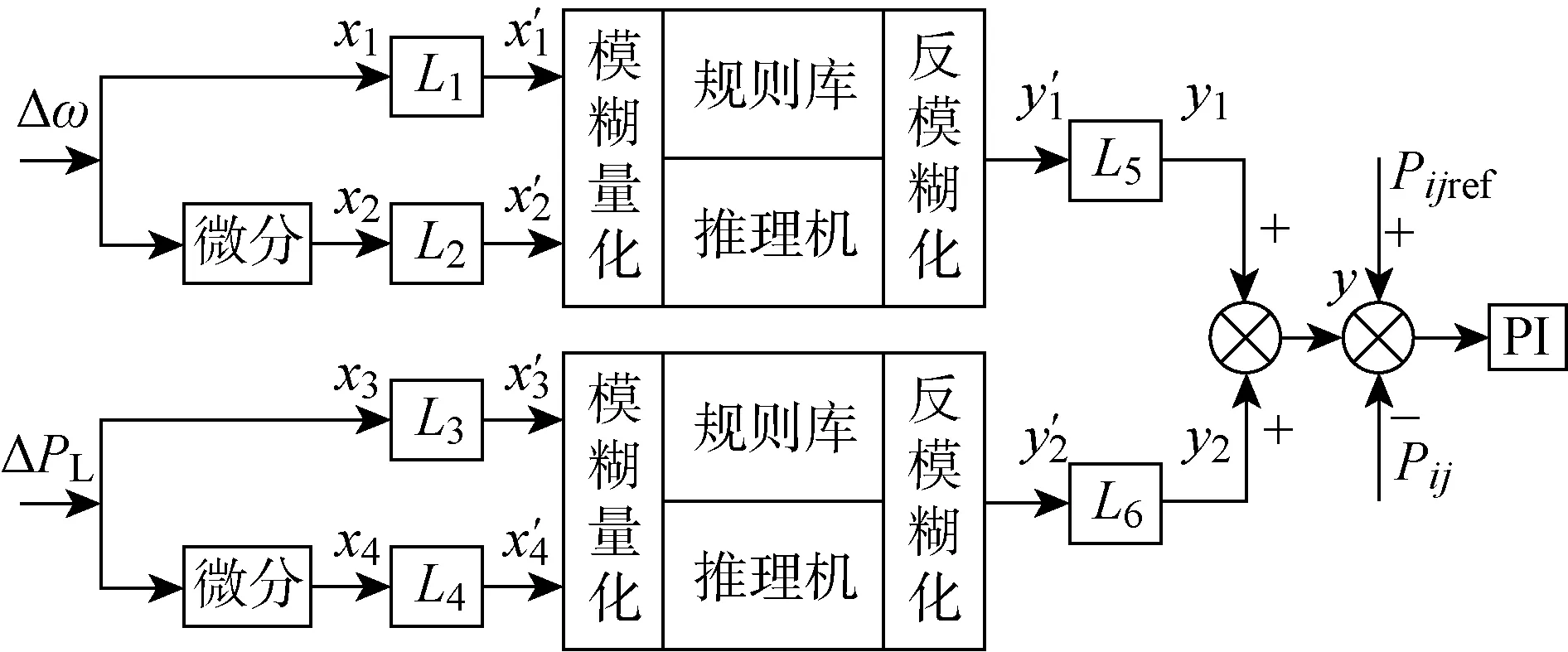
图7 IPFC模糊逻辑控制器结构图Fig.7 Structure diagram of IPFC fuzzy logic controller

接着确定控制规则表.将输入变量与输出变量均表述为“正大”(PB)、“正中”(PM)、“正小”(PS)、“零”(ZR)、“负小”(NS)、“负中”(NM)和“负大”(NB)组成的模糊集，设计出如表4所示的控制规则表.

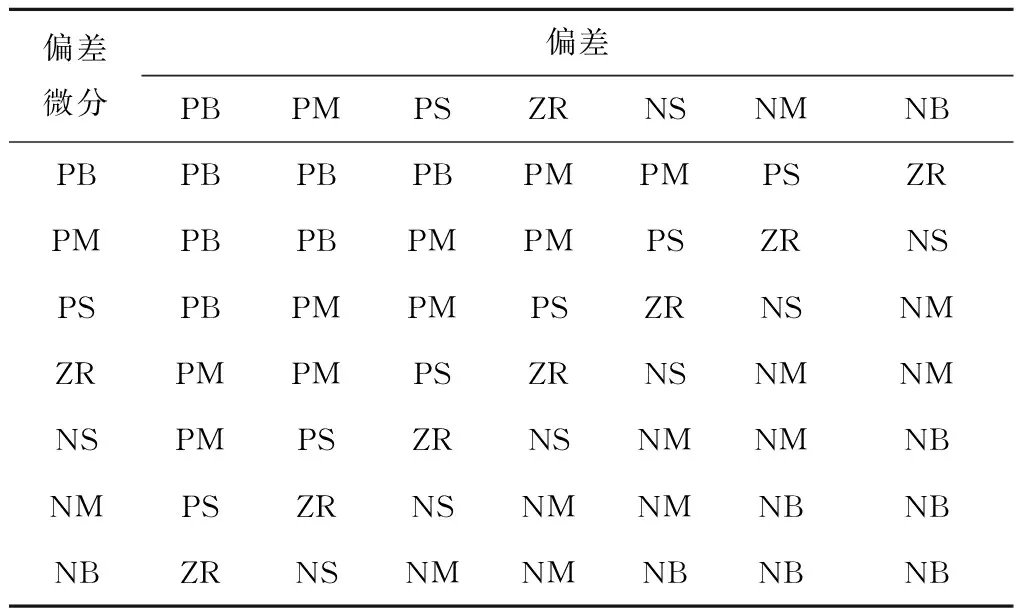
表4 模糊控制规则Tab.4 Rule of fuzzy control

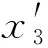
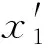
表4控制规则能够同时适应IPFC主控、辅控侧的调制要求.充分反映了人的知识及经验，并具有完备、简单、直观的优点.

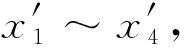
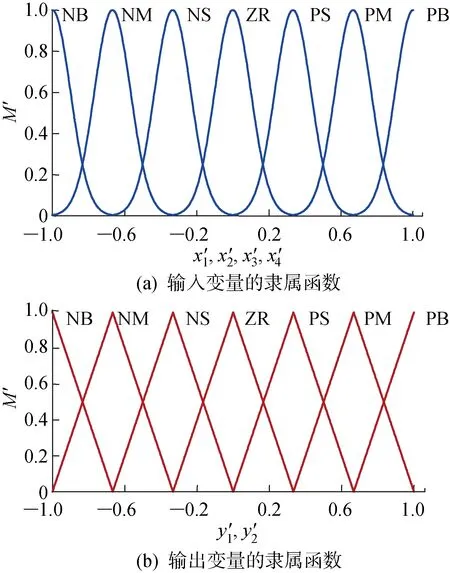
图8 隶属函数的选择Fig.8 Choices for membership function

其中，输入变量隶属函数采取具有连续性的高斯型函数，从而使隶属函数在误差接近0的区域分辨率较高，而在误差较大的区域则分辨率较低，以使系统拥有较好的鲁棒性.输出变量隶属函数则采用三角型函数，因为这种达式较为简单，形状只与直线斜率有关.与文献[16, 20]类似，模糊化采用Mamdani的最小运算规则，清晰化则采用加权平均法.

考虑到设计的模糊逻辑控制器具有较多的输入信号，而模糊规则的多样性也使得其控制范围更加广阔，模糊控制器较常规控制器具备更好的灵活性.为了进一步提高IPFC兼顾暂态稳定和小干扰稳定的同时减少暂态过程中潮流超调的能力，采用粒子群算法对控制器参数L1～L6进行优化.具体步骤如下.

步骤1确定控制器优化目标，基于时间与误差平方乘积积分(ITSE)这一性能指标设计目标函数[21]，提高暂态稳定性，增强潮流跟随性能、扰动抑制性能.

对于潮流调控，模糊控制器强制使功率跟随参考值，总体偏差越小越好，因此选取线路功率的偏差ΔPL来反应潮流超调量.对于暂态过程，如果发电机转子角度差能变小，则自然有利于功角稳定，因此选取转子角差Δδ来反映系统功角稳定性.对于阻尼控制，如果发电机转速变化率较小，则振荡抑制效果较好，因此选取转速差Δω来反映系统振荡阻尼水平.

具体目标函数J为

minJ

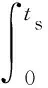
λ3(Δω(t))2]dt+Fa

(22)

式中：e(t)为优化目标；ts为采样周期；λ1、λ2、λ3均为常数；F为罚函数系数；a为与换流器容量约束条件有关的变量.

式(22)中将ΔPL、Δδ、Δω一起作为粒子群算法的优化目标，从而进一步提高IPFC兼顾暂态稳定和小干扰稳定的同时减少暂态过程中潮流超调的能力.在PL、δ、ω取标幺值的情况下，λ1、λ2、λ3可取1.当然，如果需要特别偏重某个指标，如潮流超调量ΔPL，可将λ1取得较大.罚函数中F取103，优化过程中，若满足换流器容量的约束条件，则a为0，否则a为1.具体约束条件如下：

由于换流器容量存在限制，应当使Vseij和Vseik满足以下不等式约束条件：

Vseij≤Vseij,max

(23)

Vseik≤Vseik,max

(24)

步骤2设置参数L1～L6的初始值，并采用粒子群优化控制参数.

步骤3计算目标函数值.通过在Simulink中运行与目标函数相关的仿真程序，计算式(24)的值.

步骤4判断优化后的Vseij和Vseik的值是否满足约束条件(23)～(24).若满足约束条件，则令式(22)中惩罚项的参数a取值为0.若不满足约束条件，则令式(22)中惩罚项的参数a取值为1.

步骤5判断迭代次数是否达到最大迭代次数.若否，则转步骤3，进行下一次优化迭代；若是，则选择目标函数值最小的一组参数值作为最终的最优解.

步骤6为了使控制器能够适应多种性能，应该选择对应的多种场景进行优化，具体如下：

在场景1中，t=12 s时在发电机G1机械功率中添加幅值为0.1 p.u.，频率为0.67 Hz，持续时间为0.5 s的扰动源；

在场景2中，t=9 s时在节点l处设置三相短路接地故障，t=9.15 s故障切除；

在场景3中，t=8 s时在发电机G2机械功率中添加幅值为0.2 p.u.，频率为2.67 Hz，持续时间为0.1 s的扰动源.

粒子群算法参数取值为惯性因子w为0.5，设置加速因子c1为1.5，c2为2.5，种群规模为50，迭代次数为100.优化后主要控制参数L1～L6分别取626.7、60.5、0.035、36.7、3.5及0.02.图9所示为优化过程中的具体目标函数值迭代曲线.图中E′为迭代次数.优化后的协调控制能力验证具体如第4节所示.

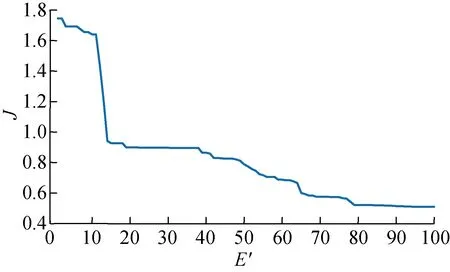
图9 粒子群优化算法迭代收敛图Fig.9 Iterative convergence graph of particle swarm optimization algorithm

4 IPFC协调控制算例验证

设置新的工况场景，验证IPFC提高系统暂态稳定和小干扰稳定的同时，减少暂态过程中潮流超调的能力，并与常见类PSS线性附加控制器作对比.安装IPFC的网架结构如图4所示.线性阻尼控制器设置参数同样设置为K=35，T1=0.2，T2=0.05，T3=0.3，T4=1.

算例1t=0时投入IPFC，t=5 s时正式启动各控制器，t=10 s时在发电机G1机械功率中添加幅值为0.15 p.u.，频率为1.67 Hz，持续时间为0.3 s的扰动源.

算例2t=0时投入IPFC，t=5 s时正式启动各控制器，t=10 s时在节点l处设置三相短路接地故障，10.15 s故障切除.

算例3t=0时投入IPFC，t=5 s时正式启动各控制器，t=12 s时将主控线路有功功率调节至2.1 p.u..

算例仿真结果如图10～13所示.图10给出了算例1中线路ij有功潮流对比.图11给出了算例1中发电机G1和G2转子角度差Δω的对比.从图10中可以看出，在加入扰动后，未投IPFC时线路功率上升到了约2.35 p.u.，投入IPFC并使用线性阻尼控制后上升到了约2.1 p.u.，而投入IPFC并使用协调控制时仅上升到了约2.05 p.u.，后者要小于前两者.并且从图11的转角差对比中可以看出，协调控制在暂态时降低了发电机功角的第一摆振幅，提高了系统的功角稳定性.

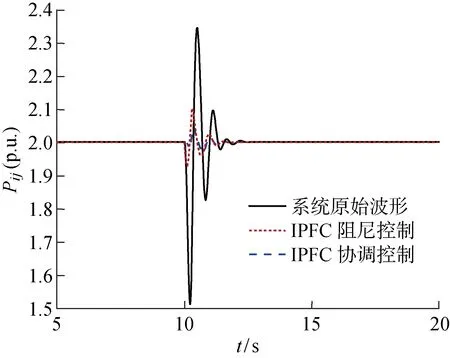
图10 算例1中线路有功潮流对比Fig.10 Comparison of active power flow in example 1

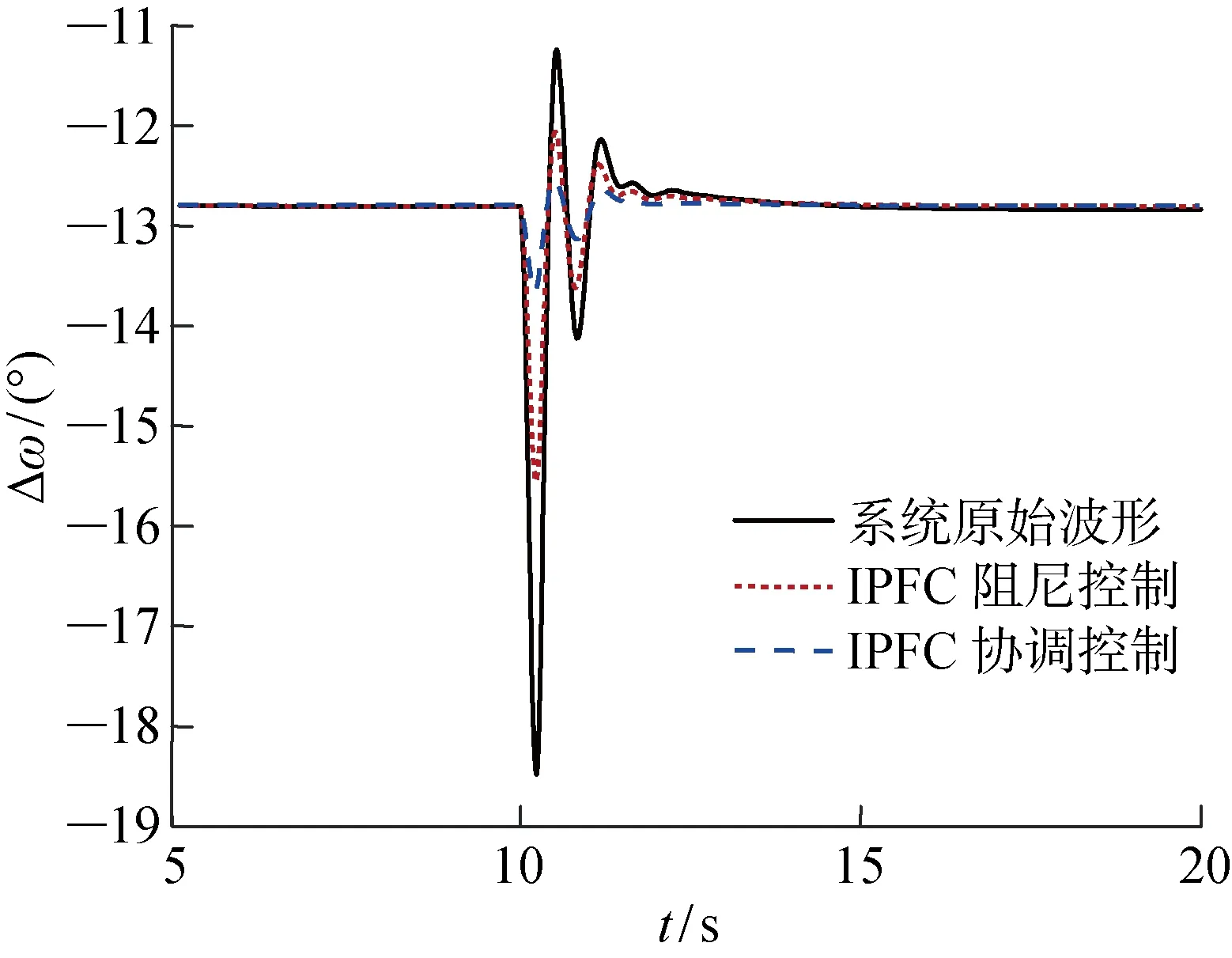
图11 算例1中转角差对比Fig.11 Comparison of angle difference in example 1

图12给出了算例2中线路ij有功潮流对比.可以看出，短路切除后，未投IPFC时线路功率上升到了约4.4 p.u.，投入IPFC并使用线性阻尼控制后上升到了约2.5 p.u.，而投入IPFC并使用协调控制时仅上升到了约2.15 p.u.，要小于前两者，保证了有功功率波动在更为合理的范围内.并且可以看出，自由振荡时，协调控制更好地增强了系统的阻尼水平，平息了系统的后续振荡.

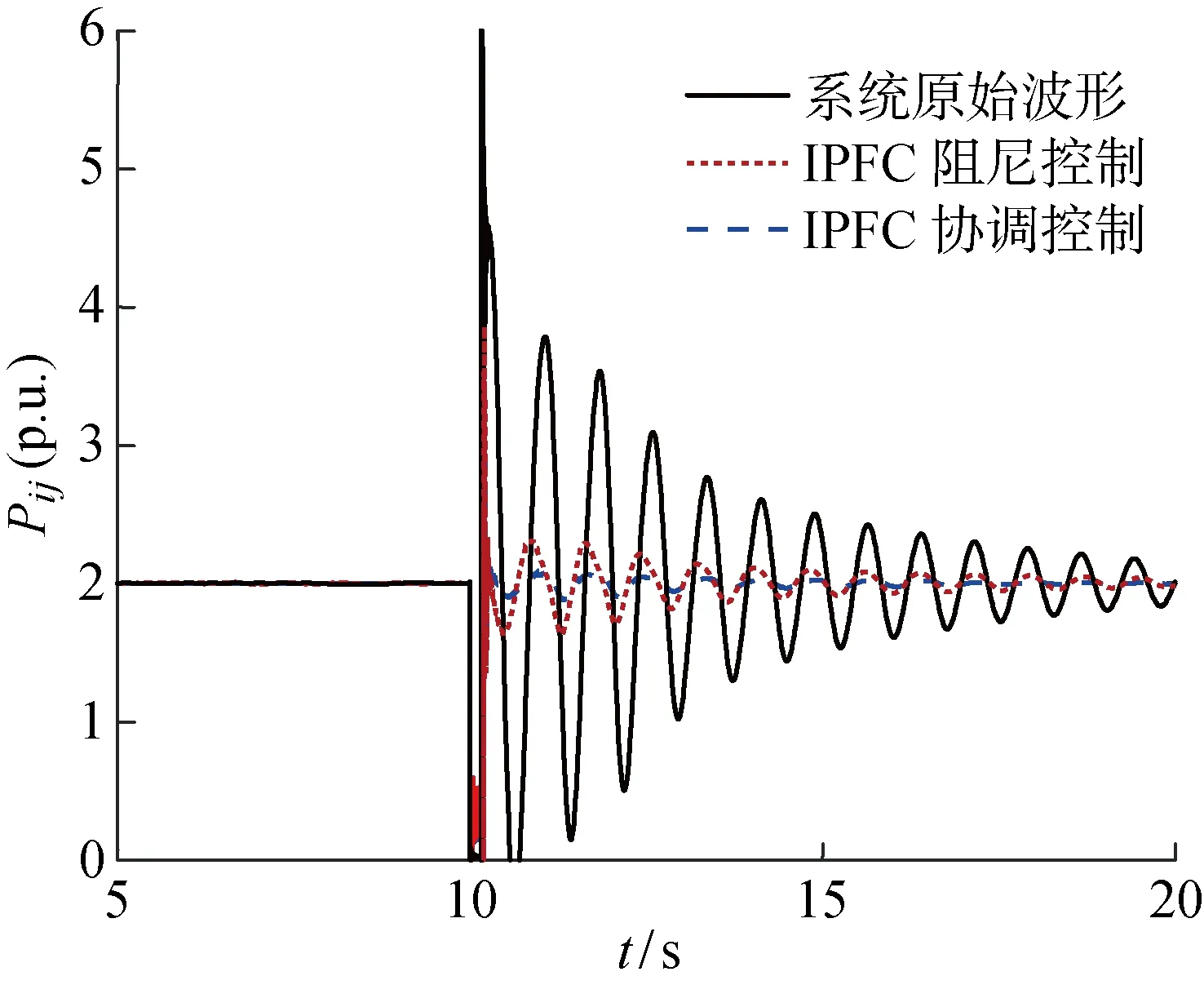
图12 算例2中线路有功潮流对比Fig.12 Comparison of active power flow in example 2

图13给出了算例3中线路有功潮流对比.可以看出，投入IPFC并使用线性阻尼控制后最大超调量约为0.08 p.u.，而投入IPFC并使用协调控制时仅超调了约0.025 p.u.，可见，协调控制较好地限制了潮流的超调量，能更好更快地追踪到目标参考值.

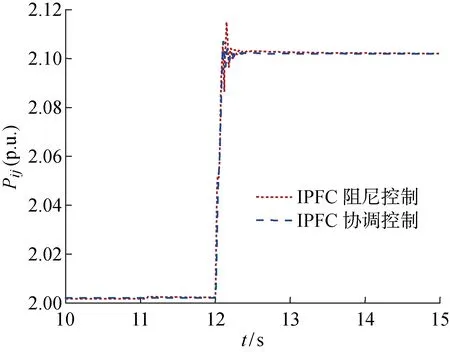
图13 算例3中线路有功潮流对比Fig.13 Comparison of active power flow in example 3

综合3个算例可见，所提IPFC协调控制策略在提高了系统暂态稳定和小干扰稳定的同时，减少了暂态过程中的潮流超调，且可适应于多种运行场景，具有较好的泛用性，有利于考虑安全性和稳定性的电力系统低碳运行.

5 结论

为了更有效地解决“双碳”背景下，电力系统负荷消纳增加、惯性降低、随机波动性增大所带来的稳定控制难题，研究了IPFC多目标协调控制策略.采用MRGA算法和Phillips-Heffron模型，量化了IPFC控制目标间的交互影响，选择了附加控制器的叠加位置，削弱了稳态调控与动态控制间的交互影响.进一步地，针对暂态过程，设计了模糊逻辑控制器及协调策略，结合粒子群算法优化了控制器参数，在提高了暂态稳定和小干扰稳定的同时，减少了暂态过程中的潮流超调，增强了IPFC在不同系统运行工况下的协调能力，为装置在实际工程应用中的协调控制提供技术支撑，有利于考虑安全性和稳定性的电力系统低碳运行.