后疫情时期机场起降量预测方法

杨璐，李印凤，2，刘伟，刘金伊，邢警长，傅子涛

( 1.华北理工大学 建筑工程学院，河北 唐山 063210；2.空中交通管理系统与技术国家重点实验室，江苏 南京 210007；3.中国民用航空华北地区空中交通管理局，北京 100621)

引言

随着国家民航事业的飞速发展，旅客运输成为民航主要业务之一，机场起降量短期预测对民航建设具有重要意义。从"十二五"期间至今我国民航业一直持续发展，国家和地方政府对民航发展的支持和重视度也开始逐步加大。以石家庄为例，石家庄是河北省重要的交通枢纽，机场起降量架次可以直接反映出民航运输发展情况，还可以间接地反映出河北省的社会经济情况。因此，疫情恢复期机场起降量预测至关重要。目前主要预测方法包括：时间序列法、灰色预测法、神经网络法、支持向量机法等，这些预测方法分为两大类[1]：一类是基于线性理论的时间序列法如灰色预测法等模型；另一类是基于非线性理论如神经网络，支持向量机等模型。2014年李印凤、谢华[2]基于Fratar交通分布预测模型，对预测年度全国航班分布进行预测，得出目标机场的航班时刻需求。2015年李印凤[3]以计量经济预测、BP神经网络预测和灰色数列预测为基础，基于熵权组合预测模型预测全国机场起降总量。2019年李杨[4]运用灰色预测模型 GM(1,1)、Logistic群体增长模型对航班起降量进行预测并发现LPGM模型预测优于GM(1,1)模型。2019年朱贾悦、方雨晨[5]等人运用ARIMA模型和灰色预测对成都双流机场旅客吞吐量进行预测。同年王瑞璇[6]使用BP神经网络预测法对终端区年起降量需求预测。

以上传统方法只能定量预测，目前由于疫情因素的影响不能完全采用定量分析，需考虑环境的因素，采用定量与定性相结合方法对后疫情时期机场起降量分析预测，该项研究的预测思路为：首先构建基于多元线性回归与灰色预测组合模型来预测总机场起降量，再根据国内外航班量分配情况，取各自平均值作为国内外分配系数，将国内外分配系数分别乘以总起降量预测值得到国内外航班量。再分别对国内外航班量进行修正，修正后的结果作为后疫情时期机场总起降量。图1所示为该过程的流程图。

图1 流程图

1 机场起降量组合预测方法

1.1 基于多元线性回归预测机场起降量模型

多元线性回归模型研究因变量与多个自变量之间的线性关系，从而建立线性函数表达式。而影响因变量的自变量因素较多，即多元线性回归模型[7,8]表达式为：

Y=b0+b1x1+b2x2+b3x3+b4x4+b5x5+bixi+e

(1)

其中Y表示起降量架次，x1表示GDP，x2表示第三产业生产总值，x3代表社会消费品销售，x4代表人均可支配收入，x5代表公路客运量，x6代表入境旅客人数，b0为常数项，b1,b2…bi是回归系数，e是随机误差。

设有n维数组用矩阵形式表示为：

记为Y=XB+E。

利用最小二乘法求回归系数矩阵B

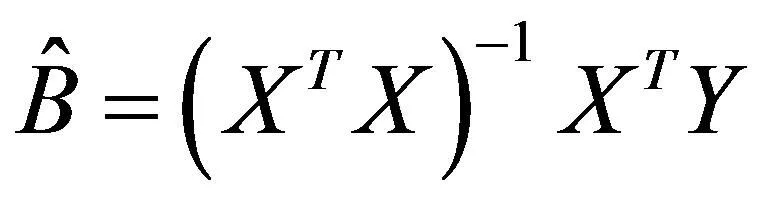
(2)

检验分析分为拟合优度检验(R2)，方差显著性F检验，参数显著性t检验，拟合优度检验是检验回归方程对样本观测值的拟合程度。回归方程完全拟合样本观测值R2等于1。R2越接近1说明回归方程的拟合优度精度越准确。

1.2 基于灰色GM(1,1)机场起降量预测模型

灰色预测模型可解决数据量较少(一般4个数据就够)，并可解决序列完整性及可靠性低的问题。可将无规律性的数据序列经过一系列累加过程生成有序性的重组数据，其本质是在生成的重组数据上建模，用微分方程分析过程。灰色预测适用于短期预测，比如航班数量预测等。灰色GM(1,1)模型[9]是一阶线性动态模型，建模过程如下：

(3)构建矩阵系数B，Y；

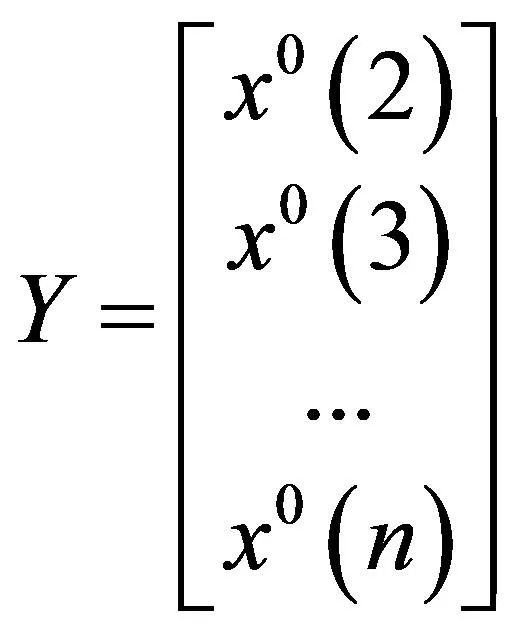
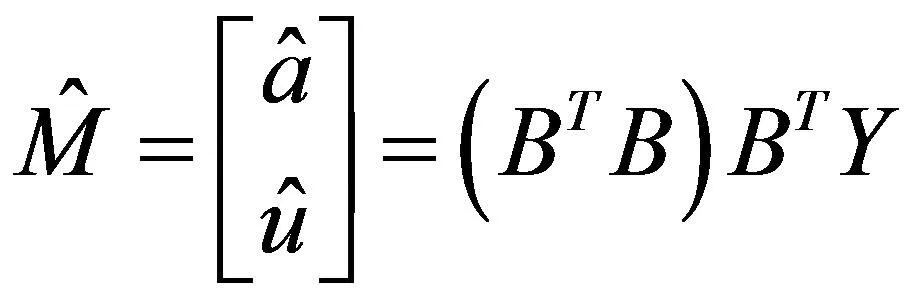
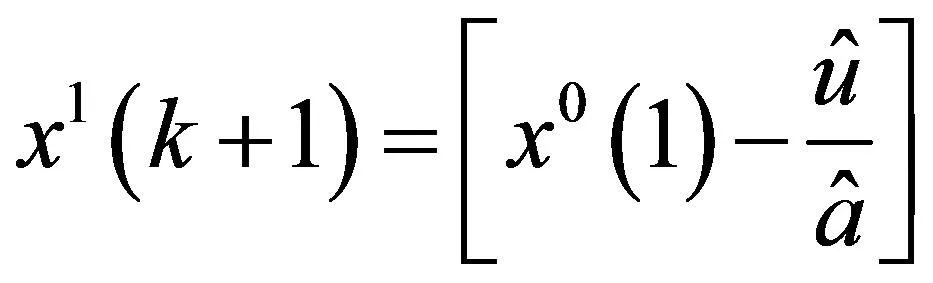
1.3 基于组合预测法预测机场起降量模型

针对单一模型预测具有一定的局限性。采用组合预测模型既吸收了多元线性模型的优点又考虑了灰色预测模型优点，使预测结果具有全面性。然而权重的合理选取至关重要。运用加权系数法确定组合预测模型。权重计算方法为：分别计算出多元回归模型预测与灰色预测模型的误差平方和，然后算出2种模型误差平方和最小的原则对各单项预测模型的权数再进行赋值。

(3)

(4)

则组合模型的预测结果可表示为:

(5)

其中e1为多元线性回归模型误差平方和，e2为灰色模型误差平方和，w1为多元线性回归权重系数，x1为多元线性预测值，w2为灰色模型权重系数，x2为灰色预测值。

2 后疫情时期机场起降量预测修正方法

2.1 国内国际航班量分布分析

根据国内国际航班量总起降量历史数据，利用式(6)、式(7)求取历年国内航班量占总起降量比例系数与国际航班量占总起降量比例系数，从历年国内外占比情况分析，比例系数基本保持稳定。可利用式(8)、式(9)求取各自平均值作为国内外航班量占总起降量的分配系数，根据分配系数以及机场总起降量预测值分别得出国内航班量与国际航班量。

(6)

(7)

Ni为国内航班量占比，fi为国内航班量，mi为国际航班量，Mi为国际航班量占比

(8)

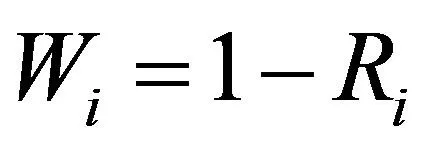
(9)

Ri-国内航班量占比平均值，

Wi-国际航班量占比平均值。

2.2 国内国际航班量预测修正

国内航班量修正：建立平均偏差程度修正系数。平均偏差程度修正的关键是求出平均比率。平均比率是各年实际数与预测数之比的算术平均值，利用公式(10)求出平均比率，平均偏差程度为平均比率-1式(11)，将预测值乘以平均比率作为修正后的预测结果。

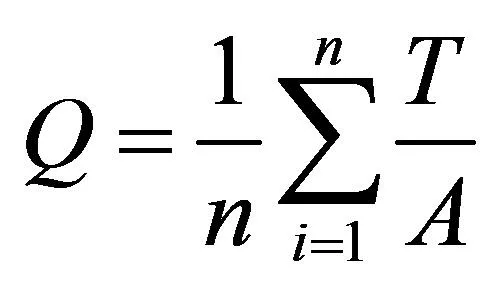
(10)

T—国内航班量实际值，架次

A—国内航班量预测值，架次

(11)

Q—平均比率

国际航班量修正：目前国际疫情处于危险时期，根据疫情前(未受疫情影响)与疫情后建立疫情影响占比参数Ki进行修正，随着时间的变化疫情逐步缓解，每年疫情影响占比参数Ki以恢复因子R逐年减少，建立初始疫情影响占比参数为K1，K1求得，减去恢复因子R求得下一年参数K2，以此类推求出各年疫情影响占比参数Ki(12)，将各年修正前国际航班量(疫情前航班量)预测值带入公式(13)求出疫情后的国际航班量(修正后)。

(12)

(13)

Vi-修正前国际航班量，架次；

Pi-修正后国际航班量，架次；

Ki-疫情影响占比参数。

3 石家庄机场起降量预测实例分析

基础数据：根据石家庄市统计年鉴以及官方网站统计出以下数据(如表1所示)，表1的数据包括影响机场起降量的有关因素，GDP(x1)，第三产业生产总值(x2)，社会消费品零售(x3)，人均可支配收入(x4)，公路客运量(x5)，入境旅客人数(x6)。对历史飞行计划数据进行预处理，获得2015年到2018年每年的国内航班量与国际航班量，如表1国内和国际起降量数据。

表1 2010～2018年机场起降量与各影响因素

首先应对选取数据的自变量与因变量相关性进行分析。影响机场起降量相关性大的主因素为GDP相关系数0.774，第三产业生产总值相关系数0.903，社会消费品零售相关系数0.835，入境旅客人数相关系数0.827。影响机场起降量相关性小的次因素为人均可支配收入相关系数0.635和公路客运量相关系数-0.799。利用SPSS软件构建机场起降量与GDP，第三产业生产总值、社会消费品零售、人均可支配收入、公路客运量、入境旅客人数多元线性模型，输出结果为：

y=46250.479-12.371x1+118.065x2-24.265x3-5.503x4+5.027x5-0.309x6

(14)

其中y代表机场起降量，x1代表GDP，x2代表第三产业生产总值，x3代表社会消费品零售，x4代表人均可支配收入，x5代表公路客运量，x6代表入境旅客人数。

依据容忍度或VIF(方差膨胀系数)判断自变量之间存在大量共线问题，共线变量应剔除出去。采用逐步回归法可知社会消费品销售(x3)、人均可支配收入(x4)、公路客运量(x5)与入境旅客人数(x6)之间存在共线性被剔除掉，可知影响机场起降量的主因素为GDP(x1)和第三产业生产总值(x2)。模型拟合度R2为0.92，拟合程度较好，方差结果分析P=0.001<0.05，说明线性回归方程显著。回归方程模型F检验=30.955，回归系数t检验为P1=0.003，P2=0.031均小于0.05，说明自变量对因变量显著性水平很高，最终建立模型为：

y=4 977.619-15.913x1+39.490x2

(15)

灰色预测根据1.2原理，利用MATLAB软件预测出结果，利用1.3章节公式得组合预测权重系数分别为0.34和0.66。3种模型确定，根据不同模型预测2010～2018年的预测值，如表2所示。图2所示为2010～2018年各模型预测曲线与实际值拟合图。

表2 3种模型预测值

图2 2010～2018年各模型预测曲线与实际值拟合图

通过图2显示组合模型优于单项模型，避免了单一模型的局限性与预测的偶然性。整体分析较好与实际值更贴合。由此用组合模型预测的结果作为2019～2023年机场起降量。表3所示为3种模型2019～2023年预测起降量值。

表3 3种模型预测值

国内部分：由表1可知。2015～2018年国内航班量占总航班量的比值分别为0.92、0.95、0.97、0.96。比例分配处于平稳状态，可取平均值(0.92+0.95+0.97+0.96)/4=0.95作为国内航班占总航班量的比例系数，国际航班量占总航班的0.05。国内航班量：国际航班量=19：1。按19：1分配2021～2023年总起降量得到2021～2023年国内航班量与国际航班量。由公式(5)求出疫情时期2019和2020年平均比率为80%，实际航班量与预测航班量平均偏差度为0.2，按修正系数0.8对 2021～2023年国内航班量修正。

表4 2021～2023年修正后国内外航班量及总起降量

国际部分：2020年国际疫情较严重航班量大幅度减少。经统计知2020年疫情影响后的国际航班量为1 387架，疫情前(未受疫情影响)的国际航班量为5 014架，根据疫情前后可建立疫情影响占比参数K1=(5 014-1 387)/5 014=0.72，(2020年受疫情影响航班量减少72%)。依据国际航空运输协会(IATA)官方报告全球客运量要到2024年才能恢复到COVID-19之前的水平。则2024年疫情影响占比参数K5=0，根据主观预测2020～2024年国际航班量每年以恢复因子R=0.18稳步恢复可求出各年疫情影响占比参数，各年国际预测值已知利用公式(13)得出2021～2023年国际航班量修正结果。国内外航班量修正结果表4所示。

4 结论

(1)分析发现组合预测法既吸收了多元回归线性模型的优点，又结合了灰色预测的优点。预测结果整体更具说服力。

(2)新冠疫情对全球航空运行均产生了巨大影响，后疫情时期机场起降量预测是开展机场保障、航空公司航线恢复等工作的基础。

(3)总结了后疫情期间机场起降量预测结果具有现实意义，为未来几年机场飞机运行量提供参考依据。可评估其他机场甚至全国机场的恢复趋势，机场起降量的预测不仅能反映出疫情缓解的趋势，同时能使航司合理安排飞行数量，提高效率。