基于奇异值差分序列的信号降噪处理方法研究

季景方

基于奇异值差分序列的信号降噪处理方法研究

季景方1,2

（1.湖北汽车工业学院汽车工程学院，湖北 十堰 442002；2.汽车动力传动与电子控制湖北省重点实验室，湖北 十堰 442002）

奇异值分解是一种十分有效的信号降噪处理方法，但奇异值个数的选择对信号降噪的影响巨大。文章由奇异值序列构造奇异值差分序列，寻找差分序列突变位置，结合不同信号差分序列的特征提出了确定奇异值个数的方法。将提出的选择奇异值个数的方法应用于三种模拟信号降噪中，降噪结果表明提出的方法可以达到有效滤除噪声的目的。

奇异值分解；奇异值差分序列；信号降噪

引言

旋转机械是机械设备中关键的一类部件，对现代工业的发展起到了至关重要的作用。由于旋转机械工作环境恶劣，设备维护不及时，导致设备极易出现故障。旋转机械设备一旦出现意外故障，往往会造成巨大的经济损失和人员伤亡，因此对旋转机械设备的故障诊断具有重要的工业和经济价值[1]。振动信号分析对旋转机械设备的故障诊断是一种有效的方法，并且得到了广泛的应用，然而实测振动信号往往包含大量的噪声，这使得微弱故障特征被淹没在噪声中。对实测振动信号的降噪处理是采用振动信号对旋转机械设备进行故障诊断所面临的巨大挑战。小波变换、经验模态分解、奇异值分解（singular value decomposition，SVD）等多种信号处理技术得到了快速的发展，和小波变换、经验模态分解方法所不同，SVD是一种无需预定义基函数的非参数信号处理方法，且具有速度快、易实现的优点[2]。有效奇异值的选择对SVD降噪效果影响比较大，本文采用差分序列来选择奇异值，并将其应用于故障振动信号的处理中。

1 SVD降噪理论

矩阵A的可以表示为因式分解的形式，即：

=USV （1）

其中，=[1,2,…,u]，=[1,2,…,v]

为正交矩阵，矩阵=和的列向量分别为矩阵AA和T的特征向量。矩阵为对角矩阵，对角线上元素为矩阵按照递减顺序排列的奇异值，即=[(1,σ2, …, σ),0]，=min(,)且1≥σ2≥…≥σ。

是进行振动信号降噪处理的有效工具，振动信号降噪处理包括三步[3]：

1.1 第一步：构造Hankel矩阵

由于实测振动信号为时间序列，因此采用降噪必须将实测振动信号转化为矩阵。Hankel矩阵具有零相位移动和类小波特性，在实际中得到了广泛的应用。对实测振动信号=[(1),(2),…,()]，其对应的Hankel矩阵为：

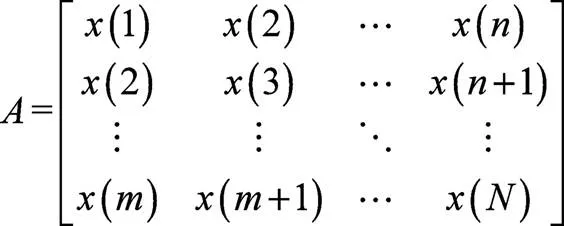
其中，=−+1，其决定了中分解组件的个数，其选择通常小于。

1.2 第二步：信号分解与重构

Hankel矩阵可以表示为m个子矩阵A的叠加，即：

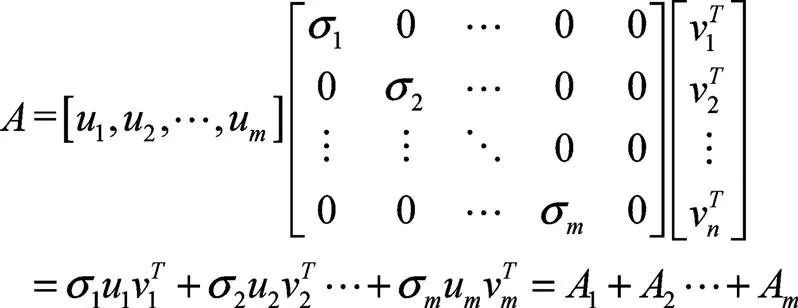
每一个子矩阵A对应原始信号中的一个奇异值分量x，x可以通过提取子矩阵A的第一行和最后获得，即：

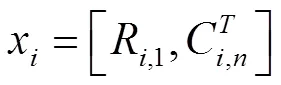
原始信号可以由各分量x线性叠加得到，即：

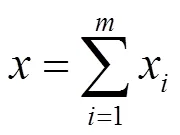
1.3 第三步：信号降噪

真实信号由比较大的奇异值所决定，因此奇异值的选择直接决定了降噪的效果。选择合适的阈值，即前个奇异值，那么将降噪信号～为：

2 有效奇异值选择

信号降噪的关键是将真实信号和噪声信号分离，有效奇异值选择的关键是寻找实测信号的奇异值突变点。为了描述奇异值的突变状态，引入奇异值差分序列，即：

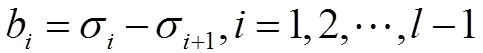
奇异值差分序列的值描述了相邻奇异值之间的变化状态。当相邻奇异值差别比较大时，在差分序列中就会存在尖峰，同时整个差分序列中必然存在最大尖峰点b，即第个位置就是奇异值发生最大突变的位置。奇异值发生最大突变的位置往往包含更多的信息，必须给予高度的关注，有效奇异值的选择流程如下：

第一步：由奇异值获得奇异值差分序列，同时确定奇异值差分最大值所对应的序列号。

第二步：如果=1，那么实测信号中包含有直流成分，继续寻找次最大突变位置，将该位置所对应的序列号作为最新的值；否则，直接进入下一步。

第三步：对比b和b的大小，其中=+1,+2,…。如果b>>b，有效奇异值个位为；否则，有效奇异值为，其中为序列{b+1, b+2,…}中最大值所对应的序列号。

在故障诊断领域，突变大的位置往往是由故障引起的结构冲击、振动等所造成的。因此，奇异值序列突变比较大的位置为真实信号奇异值和噪声奇异值的分界点，可以通过有效奇异值选择流程来确定所选择的奇异值个数，提取真实信号，达到对实测振动信号降噪的目的。

3 模拟信号降噪处理

3.1 不含直流成分的周期信号降噪

不含直流成分的信号为1=sin(2)+cos(6)，在区间[0,2π]上采样点数为512，同时将满足高斯分布(0,1)的白噪声加入信号中，获得含噪声波形，如图1(a)所示。基于512点的时间序列构造=257，=257的Hankel矩阵，同时对矩阵进行分解，获得奇异值序列波形，如图1(b)所示。由奇异值序列计算奇异值差分序列，所得结果如图1(c)所示。为了清楚展示奇异值差分序列所反映的信息，选择奇异值序列和奇异值差分序列的前50个数据绘制，结果如图1(d)所示。

由图1可知，奇异值差分序列的最大尖峰点在第4个位置。最大尖峰点为真实信号奇异值和噪声信号奇异值的分界点，因此选择前4个奇异值构成的分量进行叠加获得降噪后的信号，同时和真实信号1=sin(2)+cos(6)进行对比，结果如图2所示。

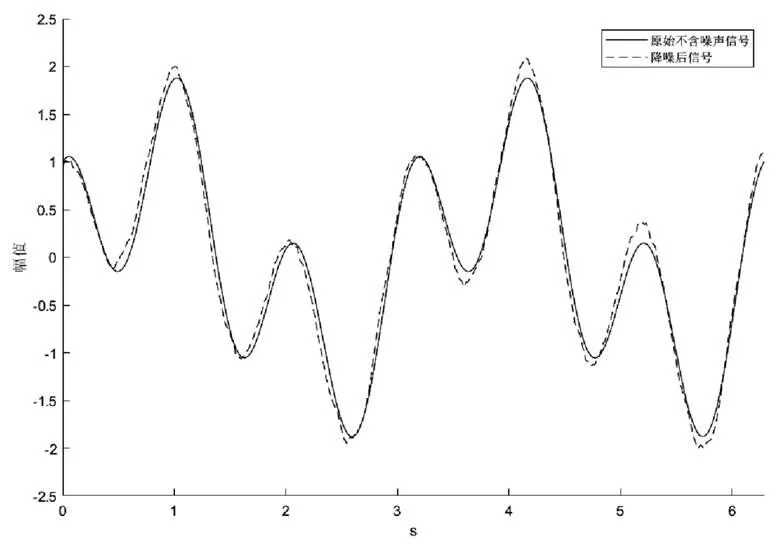
图2 降噪后信号与真实信号对比

由图2可知，采用奇异值差分序列的最大尖峰点来选择有效奇异值进行降噪处理，对含噪声信号取得了良好的降噪效果。

3.2 含直流成分的周期信号降噪

含直流成分的信号为2=1+sin(2)+cos(6)，按照3.1同样的方式加入满足高斯分布(0,1)的白噪声，获得含噪声信号的奇异值及差分序列，如图3所示。

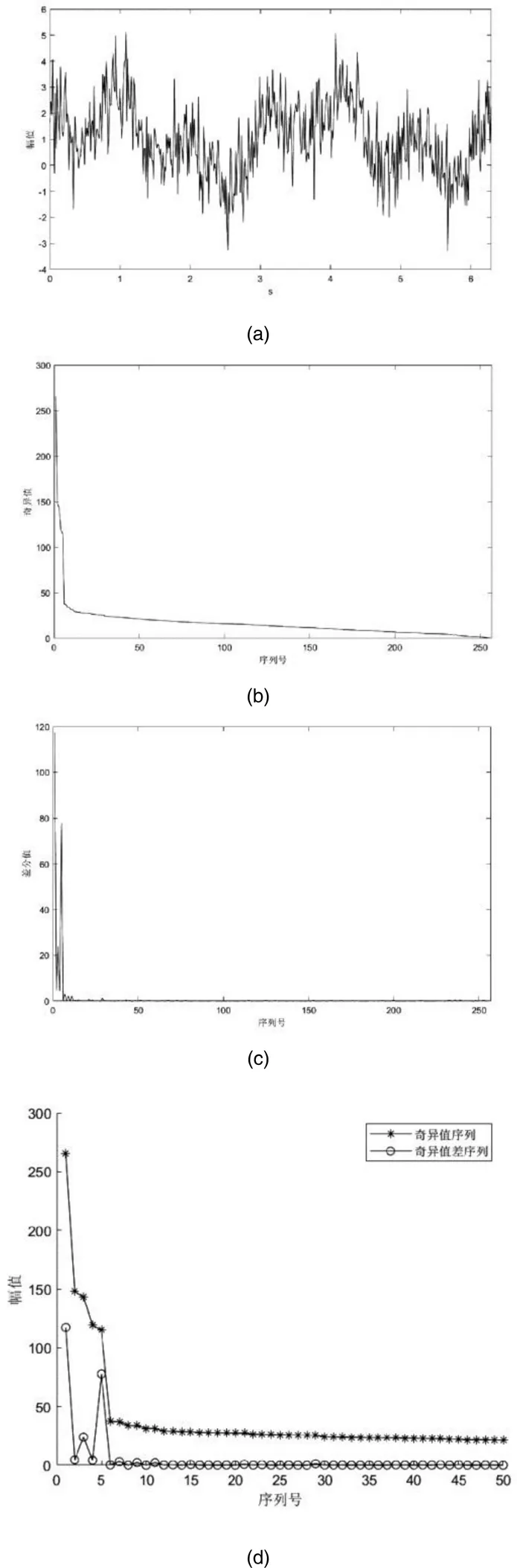
图3 信号奇异值及差分序列

由图3可知，奇异值差分序列的最大尖峰点在第1个位置，同时除了第1个值，包含直流成分信号的差分序列和不包含直流成分的差分序列非常相似。分别取前1个奇异值和前5个奇异值构成的分量进行叠加获得降噪后信号，同时和真实信号2=1+sin(2)+cos(6)进行对比，结果如图4所示。

图4 降噪后信号与真实信号对比

由图4可知，前1个奇异值分量对应的是信号的直流成分，同时采用奇异值差分序列中的第二大尖峰点来选择有效奇异值进行降噪，对含噪声信号取得了良好的降噪效果。

3.3 调频信号降噪

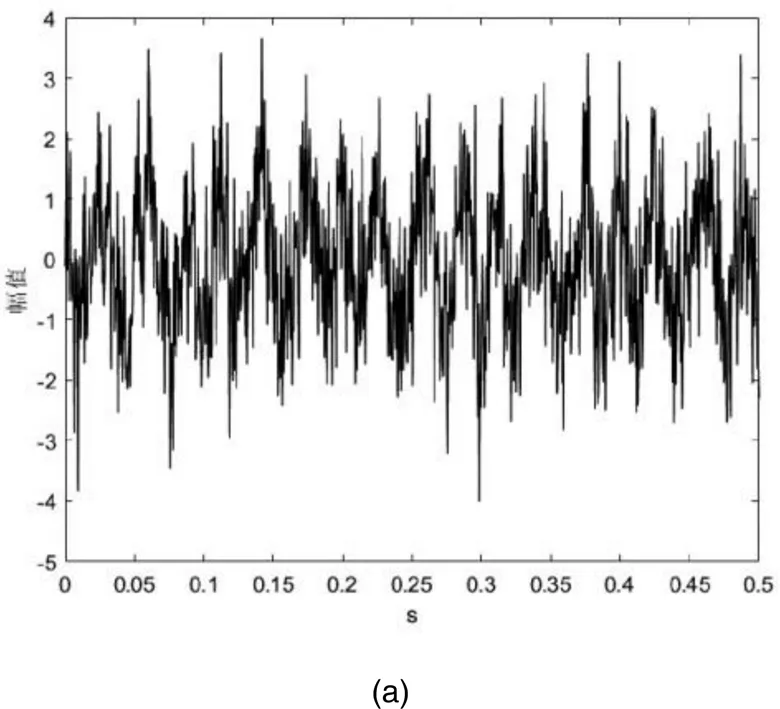
调频信号3=cos (70πt+sin (20πt))，在区间[0,0.5]上采样点数为1 024，同时将满足高斯分布(0,1)的白噪声加入信号中，获得含噪声的调频信号。按照2.1同样的方式获得含噪声信号的奇异值及差分序列，如图5所示。

由图5(d)可知，最大尖峰点在第2个位置，同时第6个位置为次大尖峰点，其余差分序列值明显偏小。分别取前2个奇异值和前6个奇异值构成的分量进行叠加获得降噪后信号，同时和真实信号3=cos (70πt+sin (20πt))进行对比，结果如图6所示。

由图6可知，当奇异值差分序列中第二大尖峰点在最大尖峰点之后，那么应该根据第二大尖峰点来选择有效奇异值进行降噪，这样才能达到良好的降噪效果。

4 结论

奇异值分解在信号降噪处理中具有广泛的应用，奇异值的选择直接影响了信号降噪处理的效果，论文通过构造奇异值差分序列，通过对差分序列突变位置的分析，提出了确定有效奇异值的方法。将提出的方法应用于三种模拟信号的降噪处理中，验证了提出方法的有效性。

[1] 吴春志,冯辅周,吴守军,等.深度学习在旋转机械设备故障诊断中的应用研究综述[J].噪声与振动控制,2019,39(5):1-7.

[2] 刘湘楠,赵学智,上官文斌.强背景噪声振动信号中滚动轴承故障冲击特征提取[J].振动工程学报,2021,34(1):202-210.

[3] 刘树聃,陈知行.奇异值分解和EEMD的非线性振动信号降噪方法[J].探测与控制学报,2019,41(3):37-42.

Research on Signal Denoising Method Based on Singular Value Difference Sequence

JI Jingfang1,2

( 1.School of Vehicle Engineering, Hubei University of Automotive Technology, Hubei Shiyan 442002;2.Key Laboratory of Automotive Power Train and Electronics, Hubei University of Automotive Technology, Hubei Shiyan 442002 )

Singular value decomposition is a very effective signal denoising method, but the selection of the number of singular values has a great impact on signal denoising. In this paper, the singular value difference sequence is constructed from the singular value sequence to find the mutation position of the difference sequence. Combined with the characteristics of different signal difference sequences, a method to determine the number of singular values is proposed. The proposed method of selecting the number of singular values is applied to the noise reduction of three analog signals. The noise reduction results show that the proposed method can effectively filter the noise.

Singular value decomposition; Singular value difference sequence; Signal denoising

U463.67

B

1671-7988(2021)23-54-05

U463.67

B

1671-7988(2021)23-54-05

10.16638/j.cnki.1671-7988.2021.023.015

季景方（1986-），男，硕士研究生，讲师，就职于湖北汽车工业学院汽车工程学院，研究方向：非平稳信号处理及故障诊断。

汽车动力传动与电子控制湖北省重点实验室创新基金项目（编号：2015XTZX043）和省教育厅项目（编号：B2020084）。