基于模态反转的半球谐振陀螺零位自校准方法*

潘覃毅，赵万良，王 伟，于翔宇，孙湘钰

(1. 上海航天控制技术研究所·上海·201109；2.上海惯性工程技术研究中心·上海·201109)

0 引 言

半球谐振陀螺(Hemispherical Resonator Gyroscope，HRG)是一种谐振式惯性敏感器，具有质量小、体积小、功耗低、工作寿命长、测量精度高、长期工作可靠等优点，适用于航天、航空、车辆、船舶等惯性导航领域。

谐振子作为半球谐振陀螺的核心部件，一般由物理化学性质稳定、高品质因数的熔融石英玻璃加工制成，并封装在真空金属罩中。谐振子的高精密加工存在缺陷，往往会引入一系列不理想因素，如薄壳壁厚、石英材料的密度分布以及金属膜层厚度的不均匀性等，都会引起半球谐振陀螺的频率裂解、阻尼不对称等固有误差[1-3]，产生半球谐振陀螺的零位误差。谐振子作为轴对称结构，引起半球谐振陀螺输出零位包括两部分，关于驻波角位置的对称零位和非对称常值零位[4]。半球谐振陀螺的非对称常值零位误差十分稳定，不易受外界环境干扰，该零位不影响陀螺测量精度；而对称性零位误差与半球谐振陀螺自身的结构参数相关，易受环境温度、电磁干扰、振动以及冲击等影响，从而产生零位漂移，因此有必要对半球谐振陀螺输出的对称性零位误差进行校准补偿。

解决陀螺零位漂移的方法一般包括温度控制[5]、建模补偿[6-7]和校准[8-9]方法。温度控制采取恒温措施，使陀螺处于稳定温度场，抑制陀螺零位的温度漂移。该方法增加了陀螺产品的体积、功耗、硬件电路成本等，同时还受设备温控精度的影响。建模补偿是通过外置热敏电阻等温度传感器采集陀螺温度，建立陀螺零位温度漂移模型，测量过程中根据陀螺实测温度进行补偿。该方法的缺点是陀螺测量精度受漂移模型准确度的影响，因此建立的漂移模型具有较大误差。零位校准的方法是基于陀螺的零位特性进行校准归零，该方法不需要额外的硬件设备，不受外界环境变化影响，但对电路控制技术具有较高的要求，而基于模态反转的电路控制技术是控制电路中常用的误差消除方法。

针对半球谐振陀螺零位漂移问题，本文研究了基于模态反转的零位自校准方法。首先，讨论了半球谐振陀螺工作机理，考虑频率裂解以及阻尼不对称误差引入非理想动力学模型，并分析了半球谐振陀螺的驻波漂移特性。其次，理论上分析了半球谐振陀螺零位自校准方法，并通过虚拟进动方法实现了驻波模态反转。最后，通过仿真和实验进行半球谐振陀螺零位自校准，验证了该校准方法的有效性。基于模态反转的零位自校准方法对半球谐振陀螺的测量精度提升和工程应用具有重大的意义。

1 半球谐振陀螺驻波漂移误差分析

半球谐振陀螺通过激起谐振子上的弹性波在陀螺旋转时产生的进动效应敏感载体角速度及旋转角度[10]。在控制作用下半球谐振陀螺维持四波腹振型振动，四波腹振型以及振动周期T内四波腹振型的变化如图1(a)和图1(c)所示。当陀螺不旋转时，波腹点和波节点的位置相对于壳体保持不变；陀螺发生旋转时，在科氏加速度的作用下，振型相对外壳体发生进动，振型相对于壳体进动角度θ与陀螺外壳体绕其固定轴旋转角度ψ的关系满足θ=-βψ，β为Bryan系数，驻波的进动效应如图1(b)所示。

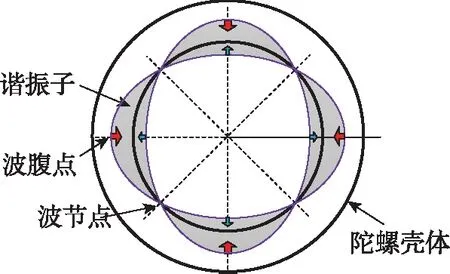
(a)静态下陀螺四波腹振型

半球谐振陀螺四波腹振动时，利用振动的分解与合成，谐振子的径向振动W(φ,t)可由关于时间和空间的函数表示，如下所示

W(φ,t)=x(t)cos2φ+y(t)sin2φ

(1)

其中，x(t)、y(t)表示0°和45°方位谐振子自由端的振动位移函数;φ为谐振子自由端的圆心角位置。

半球谐振陀螺进行物理建模时，可近似为一个二阶弹簧质量阻尼系统，其等效模型如图2所示。谐振子自由端环向密度、品质因数不均匀的四次谐波偏差导致谐振环上存在着两个分别成45°的固有频率轴系和阻尼轴系[11]，包含频率主轴和次轴、阻尼主轴和次轴。两主轴分别对应了谐振频率、品质因数的极值点。半球谐振陀螺的主轴定义如图3所示，其中，阻尼轴方位角为θτ，频率轴方位角为θω。

图2 半球谐振陀螺等效模型

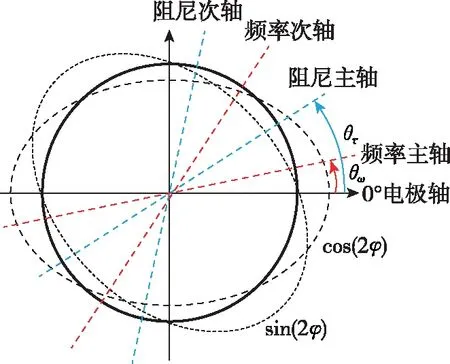
图3 半球谐振陀螺阻尼轴和频率轴定义

施加陀螺控制力作用，并考虑频率裂解和阻尼不对称误差，半球谐振陀螺的二阶动力学模型[12]为

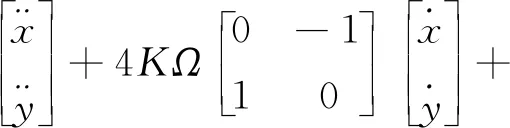
(2)

(3)

其中，ω1、ω2(ω1<ω2)为固有频率轴的谐振频率，ω为平均谐振频率，Δω为频差，矩阵Mω为频率裂解误差矩阵；τ1、τ2(τ1<τ2)分别表示固有阻尼轴的衰减时间常数，2τ-1为平均衰减时间常数，Δ(τ-1)为阻尼不对称系数，矩阵Mτ为阻尼不对称误差矩阵。fx、fy为系统施加在陀螺x、y振动方向上的控制力；K为进动因子，K≈0.277[11]；Ω为陀螺敏感角速率；meq为半球谐振陀螺等效质量。

(4)

在半球谐振陀螺的实际控制中，波腹点维持恒幅振动，波节点振动幅度为零。引入频率裂解、阻尼不对称固有误差，并分析半球谐振陀螺的固有误差影响，暂不考虑控制力作用，基于Lynch平均值法，推导半球谐振陀螺误差方程[12]为

(5)

式中，a为驻波波腹点振幅；q为驻波波节点振幅，波节点幅值也用于表征正交误差；n为谐振子环向波数，由半球谐振陀螺的工作模式决定，对于四波腹振动n=2；φ为半球谐振陀螺的振动相位。θ的微分方程表示为驻波进动误差方程，直接表述了半球谐振陀螺的测量误差特性。

由驻波进动误差方程式(5)可知，半球谐振陀螺存在电极装配偏差、阻尼不对称等非理想因素，实际的阻尼轴方位与检测驱动轴并非完全对齐，因此驻波极易发生漂移，其中阻尼不对称误差是引起驻波漂移最主要的原因[13]。

通过机械调平降低半球谐振陀螺频差Δω、正交环路抑制正交误差q，可化简驻波进动误差方程为

(6)

其中，ceq为等效阻尼不对称导致的驻波漂移函数幅值。由式(6)可知，驻波漂移误差为对称性误差，是关于驻波方位角的正弦函数关系。谐振子的阻尼不对称性受环向机械阻尼以及腔体内残余气体阻尼分布不均匀的影响，因而间接地影响半球谐振陀螺零位与驻波方位角也呈现正余弦函数。在零输入角速率下，阻尼方位角为5°，驻波的漂移速率随方位角的关系如图4所示。由图4中可知，在驻波方位角为0°和45°处，驻波的漂移方向相反，其漂移引起的零位误差同为对称性误差，本文正是基于此漂移特性进行半球谐振陀螺零位校准。

图4 驻波漂移速率随驻波方位角的变化

2 零位自校准方法

2.1 模态零位分析

在半球谐振陀螺传统PID控制模式中，控制电路主要包括3个回路：(1)幅度控制回路维持主驻波进行恒幅振动，补充阻尼机制的能量损耗;(2)正交控制回路抑制正交波振动，降低正交误差;(3)力反馈回路在波节点处施力，抑制驻波进动，保持四波腹振型的非进动状态。为激励半球谐振陀螺工作于四波腹振型，施加控制力的驱动频率与陀螺谐振频率ω保持一致，控制力表示如下

Fa=faccos(ωt+φ*)+fassin(ωt+φ*)Fq=fqccos(ωt+φ*)+fqssin(ωt+φ*)

(7)

其中，fas为相位控制力，fac为幅度控制力，fqs为正交控制力，fqc为力反馈控制力，分别表示施加在波腹点Fa和波节点Fq的控制力分量。同相cos(ωt+φ*)和正交sin(ωt+φ*)参考信号由数字锁相环跟踪实现，φ*为相位跟踪误差。力平衡模式正是通过反馈力来表征半球谐振陀螺敏感的外界角速度。

若存在外界角速度时，半球谐振陀螺受科氏力作用，四波腹振型进动，波腹点和波节点受外界角速度发生位置进动。因此施加在波腹点和波节点的控制力需要通过矢量合成的方式，旋转投影到驱动电极轴上，旋转角度即是驻波的进动角2θ。控制力的矢量合成可通过如下正交变换实现

(8)

传统力平衡模式下，驻波方位位于0°角位置(θ=0°)，即驻波工作在x模态。在x振动模态下，驻波在0°方向进行恒定振幅A0的简谐运动，振动形式为x=A0sinωxt，ωx为振动频率，而45°角位置驻波振动为0，驻波四波腹振型不发生进动。将式(7)代入动力学方程，得到x、y方向的控制力以及所施加的反馈力为

(9)

(10)

φx表示x模态跟踪相差，反馈力fqc表征外界角速度Ω，由式(10)可知x模态的标度因数为SFx=4mKA0ωx，零位为B0x=1/(4K)Δ(τ-1)sin4θτ。

当驻波工作在y模态时，驻波控制在45°角位置上(θ=45°)，即y模态的波腹轴在45°方位，波腹点振动为y=A0sinωyt，振动频率为ωy，而0°角位置的波节点振动幅度为0。φy为y模态跟踪相差，x、y方向的控制力大小为

(11)

将波腹点和波节点的振动形式以及控制力代入动力学方程，得到力反馈控制力为

(12)

当振动驻波工作于y振动模态时，陀螺的标度因数为SFy=4mKA0ωy，陀螺零位为B0y=-1/(4K)Δ(τ-1)sin4θτ。

由上述分析可知，在0°和45°不同的模态中，半球谐振陀螺的标度因数为SF≈4mKA0ωx≈4mKA0ωy，模态标度因数中仅有谐振频率不同，其余项均相同。因此，可基于电负刚度方法[14]抑制谐振子x和y方向的频差，使两者频差Δω≈0，此时认为0°与45°模态的标度因数一致，故两模态的标度因数均为SF=4mKA0ω。不同的是0°模态和45°模态的零位B0大小均为1/(4K)Δ(τ-1)sin4θτ，但两者极性相反，与上一小节的驻波漂移误差特性分析一致。因此，可通过模态反转的方式估计陀螺输出零位并对其进行校准。

图5 模态反转示意图

2.2 模态反转控制

半球谐振陀螺敏感外界角速度时，受科氏力的作用，将不同模态的能量进行交换，未消耗能量，使驻波发生进动。当外界角速度小于陀螺阈值或无外界输入角速度时，驻波不能实现进动，无法进行模态反转，因此需要在陀螺控制端施加虚拟控制力，使之具有与科氏力相同的作用，驻波发生虚拟进动，与受外界角速度影响驻波的进动效果相同。在0°和45°模态上施加虚拟科氏力如式(13)

(13)

其中，Gvirt为虚拟旋转的控制增益。

将虚拟旋转控制电压施加到x和y方向极板上，代入动力学方程可得

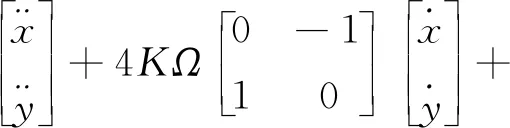
(14)

由Gvirt=4KmeqΩvirt确定虚拟转速，即一定的虚拟旋转增益Gvirt与已知的虚拟旋转速率相对应。在给定虚拟转速Ωvirt，若存在外界角速度Ω(t)，则相对于陀螺壳体驻波实际的进动角度为

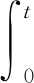
(15)

式中，θ0为驻波初始方位角，仿真中θ0=0°。通过控制虚拟旋转驻波进动角为45°，电气上旋转90°，实现模态反转，并控制半球谐振陀螺在不同模态的工作时间、工作阶段零位进行校准，模态反转的控制时序如图6(a)，模态反转过程中振动轨迹李萨如图形如图6(b)，模态反转前后陀螺零位变化如图6(c)。

(a) 模态反转控制时序图

从上述仿真可知，模态反转前后，半球谐振陀螺零位的极性发生变化。x模态的零位为36.1806(°)/h，y模态的零位为-36.6484(°)/h，满足x模态和y模态的零位大小相等，符号相反，与2.1节理论推导相同。因此，基于上述推论，可通过模态反转的电路控制技术切换输出零位，取上一时刻和当前时刻模态的零位均值，估计下一个工作阶段的半球谐振陀螺零位进行校准，以一定周期进行模态反转，对零位进行周期性校准。

3 零位校准仿真与实验

3.1 零位校准仿真

仿真中半球谐振陀螺的零位误差模型采用式(6)，零位仿真数据包括角速率随机游走和趋势项，仿真的陀螺数据和校准数据如图7所示。为验证零位校准对陀螺性能的提升，仿真中分别设置了21组不同时间(30h～60h)的原始数据，并进行零位校准，对比校准前后长期、短期(1h)的零偏稳定性(1σ)，绘制箱线图如图8所示。

图7 半球谐振陀螺零位校准仿真

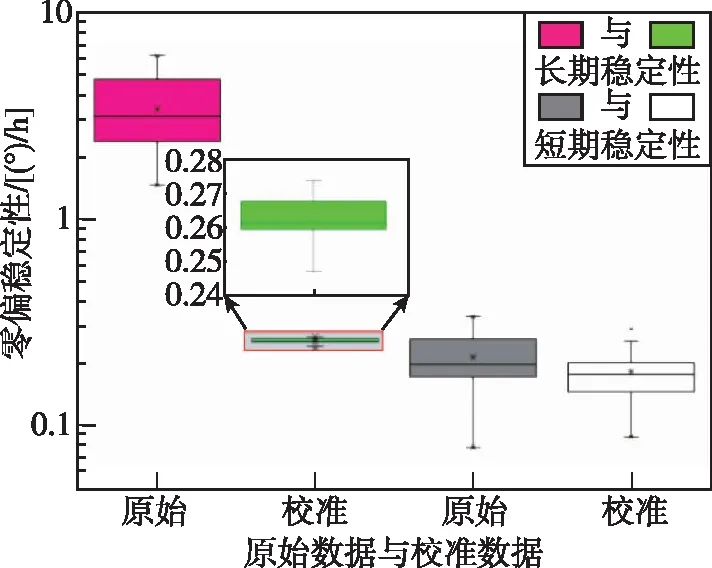
图8 零位校准对(长期、短期)零偏稳定性的影响

从仿真结果中可以看到，校准前后陀螺零位从38.8095(°)/h降低至0.0019(°)/h，大大降低了零位漂移误差。基于模态反转的零位校准方法大幅度地提高了长时间的零偏稳定性，长期零偏稳定性提高一个数量级，同时也提高了短期的零偏稳定性(中位数)，因此通过仿真验证了模态反转的零位校准方法抑制零位漂移的有效性。

3.2 零位校准实验

半球谐振陀螺控制系统主要包括陀螺表头、前端模拟电路和FPGA数字控制系统，陀螺控制系统结构框图如图9所示。前端模拟电路模块主要包括电荷放大器、差分滤波电路以及AD/DA、驱动电路。其中，电荷放大器用于检测陀螺微弱振动信号，将其转为电压信号；差分滤波电路则对输出进行放大滤波，可抑制共模噪声，提高差模信号；AD/DA完成模拟信号与数字信号的转换，用于陀螺的数字控制实现；驱动电路实现陀螺控制力的驱动放大作用。陀螺检测的微弱信号经过锁相环PLL实现频率跟踪，并进行解调滤波，组合运算以及环路误差计算后，通过PID控制器进行半球谐振陀螺的闭环控制。

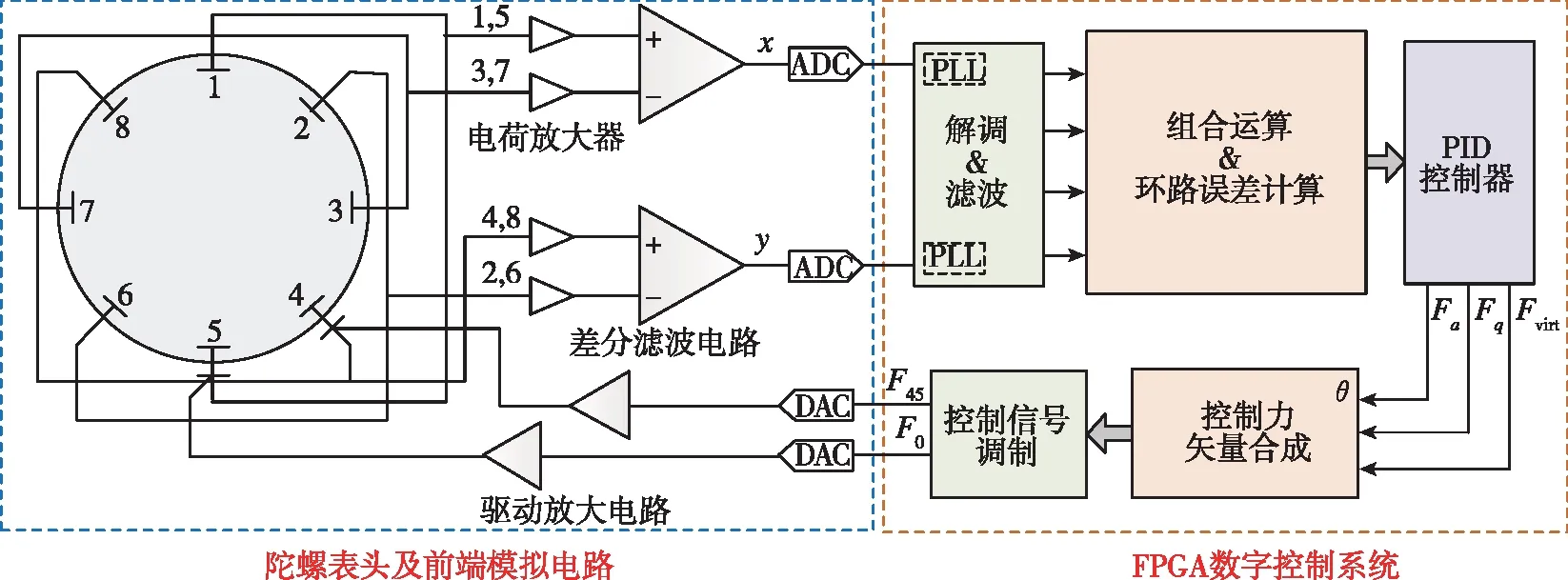
图9 半球谐振陀螺控制系统

通过上位机软件输入半球谐振陀螺的控制参数，并在半球谐振陀螺起振及控制稳定后进行模态反转控制。模态反转的控制周期为12min，受半球谐振陀螺高Q值以及控制电路实际的物理电压限制，模态反转间隔时间为1min，模态反转驻波方位控制如图10所示，模态反转前后输出零位如图11所示。

图10 模态反转驻波方位控制

图11 半球谐振陀螺模态反转前后输出零位

由图11可以看到，模态反转前后陀螺的零位值分别处于零刻度线的两侧，满足零位符号相反，x和y模态零位大小为11(°)/h和15(°)/h。根据模态反转前后的输出零位，取零位均值估计下一个工作阶段的陀螺零位，重复进行模态反转，实现零位的周期性校准。校准前0°和45°模态零位大小以及校准后结果如图12和表1所示。

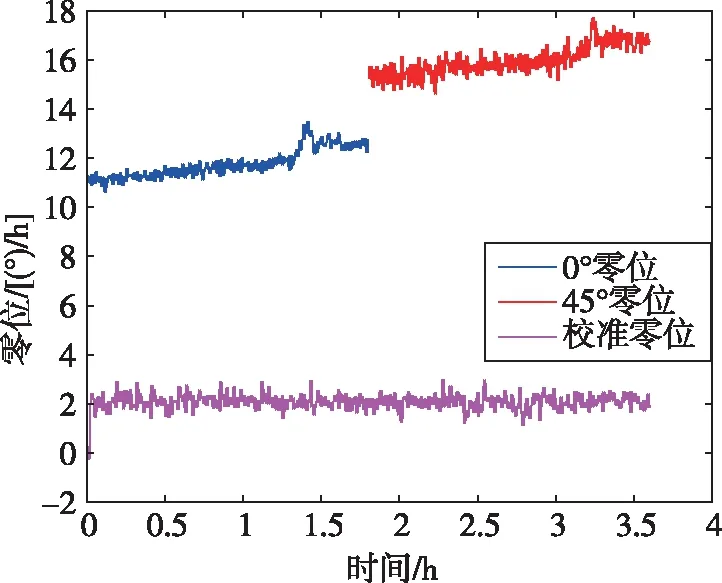
图12 不同模态零位及校准零位曲线

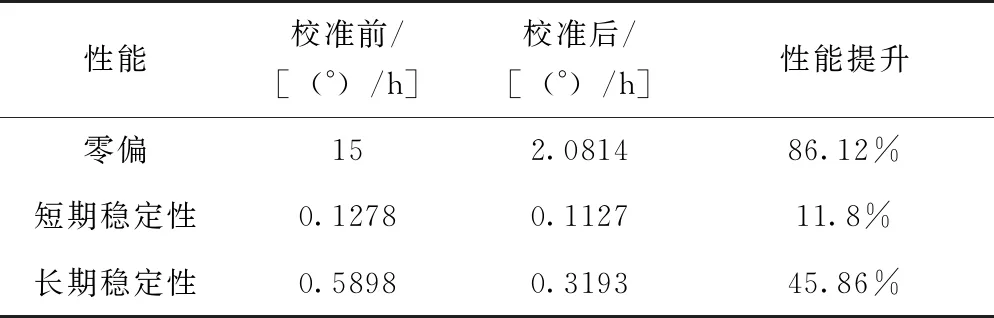
表1 原始输出与零位自校准输出对比

从表1中可以得到，相对于传统力平衡模式，校准后陀螺零位大幅下降，从15(°)/h降低至2.0814(°)/h，降低了86.12%，长期稳定性和短期稳定性也有所提高，分别提高了45.86%和11.8%。结果表明,基于模态反转的零位校准方法可有效地抑制对称性零位漂移和降低零位误差。3.1节仿真长期稳定性提高了一个数量级，实验结果与仿真具有一定的差异性，说明了半球谐振陀螺实际精度仍受频率裂解、正交误差等影响，因此后期仍需进一步研究半球谐振陀螺的误差模型，优化校准算法,提高测量精度。

4 结 论

本文提出了基于模态反转的半球谐振陀螺零位自校准方法，解决了半球谐振陀螺的零位漂移问题。首先，讨论了半球谐振陀螺的工作机理，分析了阻尼不对称引起的驻波漂移误差特性。其次，建立半球谐振陀螺零位校准方法并通过虚拟进动控制实现了模态反转。最后，对半球谐振陀螺零位自校准进行了仿真和实验。结果表明，校准零位大幅下降，从15(°)/h降低至2(°)/h，零位均值降低了86.12%，长期零偏稳定性和短期稳定性也提高了45.86%和11.8%，有效降低了陀螺测量误差，进一步验证了基于模态反转的半球谐振陀螺零位自校准方法的有效性。