基于复杂网络的Psor链路预测算法*

邹 列,张月霞,b,c

(北京信息科技大学 a.信息与通信工程学院；b.现代测控技术教育部重点实验室；c.高动态导航北京市实验室,北京 100101)

0 引 言

现实生活中，许多复杂系统都可以用节点和连线的方式表示成复杂网络，通过科学的方式研究复杂网络可以更好地认识和理解复杂系统的内部结构信息。链路预测是研究复杂网络的方式之一，是指通过已知的各种信息(网络拓扑结构、节点属性等)预测网络中尚不存在连边的两个节点之间产生连接的可能性。这种预测既包含了对未知链接的预测，也包含对未来链接的预测[1]。目前，链路预测在网络演化规律的研究中被广泛应用，具有巨大的实际应用价值。如：在微博和博客的社交网络[2-3]中，根据用户在社交平台上的社交关系信息，预测两个陌生好友进行交互的可能；在商品购买系统以及新闻、音乐、直播类娱乐系统中，通过用户的个人需求和动作行为，预测用户所需的信息，从而推荐相应的商品和相关喜好内容[4-5]。因此，对复杂网络的链路预测问题的研究有着现实意义。

链路预测方法主要分为基于机器学习的方法[6]、基于最大似然概率的方法[7]和基于网络拓扑结构的方法[8]。基于机器学习、最大似然概率的方法虽然能得到较高的精确度，但是其复杂度很高，应用范围受到了限制。基于网络拓扑结构的方法利用拓扑结构使得链路预测更容易实现，备受多数研究人员的关注。现有的基于网络拓扑结构的相似性预测算法分为局部、全局和准局部相似性算法[9]。文献[10-15]基于网络拓扑结构的相似性算法更多的是关注共同邻居节点数目、节点的度、共同邻居节点的度以及节点间传输路径能力，而忽略了邻居节点的度的影响，不能够相对全面地获取网络的拓扑信息，以至于链路预测的精度不够高。

针对基于网络拓扑结构的相似性算法的问题，本文提出了一种基于复杂网络的Psor链路预测算法，并通过5个真实网络数据验证了所提算法的有效性。

1 Psor算法原理

1.1 网络描述

假设网络是简单无向无权网路G(V,E)，其中V是网络中节点的集合，E是网路中边的集合。网络中有N个节点，M条边，即|V|=N，|E|=M。网络中任意两个节点可能产生边的情况有N×(N-1)/2种。令U为节点对组成边的全集，那么节点对没有连接边的集合为U-E。假设集合U-E中有丢失的连接或者将来会出现的连接，链路预测就是找出这些连接。

无向无权网络G(V,E)可以用邻接矩阵A表示。如果节点i和节点j之间有边连接，则aij=1；否则aij=0。通过邻接矩阵可以计算网络每个节点的度，节点i的度可以表示成

(1)

根据特定的相似性链路预测算法，为网络中两个节点之间没有连边的节点对(x,y)赋予一个分数Sxy，以估计它们未来连接的可能性。将所有未观察到的连接均根据其得分进行排名，分数值越大，这两个节点连接的可能性就越大。

1.2 Psor算法

2010年印度学者Prathap提出的一种新型综合性学术评价指标，称为P指数[16]，其计算公式为

p=(C2/N)1/3。

(2)

式中：C为学者发表的文章被引频的总次数，N为学者发表的文章数。由此可以看出，P指数在学术评价中体现了数量(发文量)与质量(被引频的次数)的平衡，使得评价一个学者的科研水平更有效。

以此类推，将P指数的概念扩展到复杂网络中。在复杂网络中，一个节点的邻居相当于学者的发文数，其节点邻居的邻居相当于学者发表的文章被引用的次数。本文综合节点自身的度和邻居节点的度定义了节点的Psor指数，其计算公式为

Psorx=((∑ki)2/kx)1/3。

(3)

式中：i为节点x的邻居，kx和ki分别表示节点x和节点i的度。由此可以看出，式(3)中节点的Psor指数大小由节点的度和其邻居节点的度共同决定。当节点的度一定时，其邻居节点的度越大，节点的Psor指数越大，即该节点的影响力就越大。与现有的链路预测指标仅将节点度视为节点的影响资源相比，节点的Psor指数可以更广泛地量化节点的影响。

下面举例说明节点的Psor指数对链路预测的精度的影响。如图1所示，(a)和(b)是两个复杂网络，被预测节点为x和y，节点x和节点y的度都为4，它们的共同邻居都是节点A和节点G。

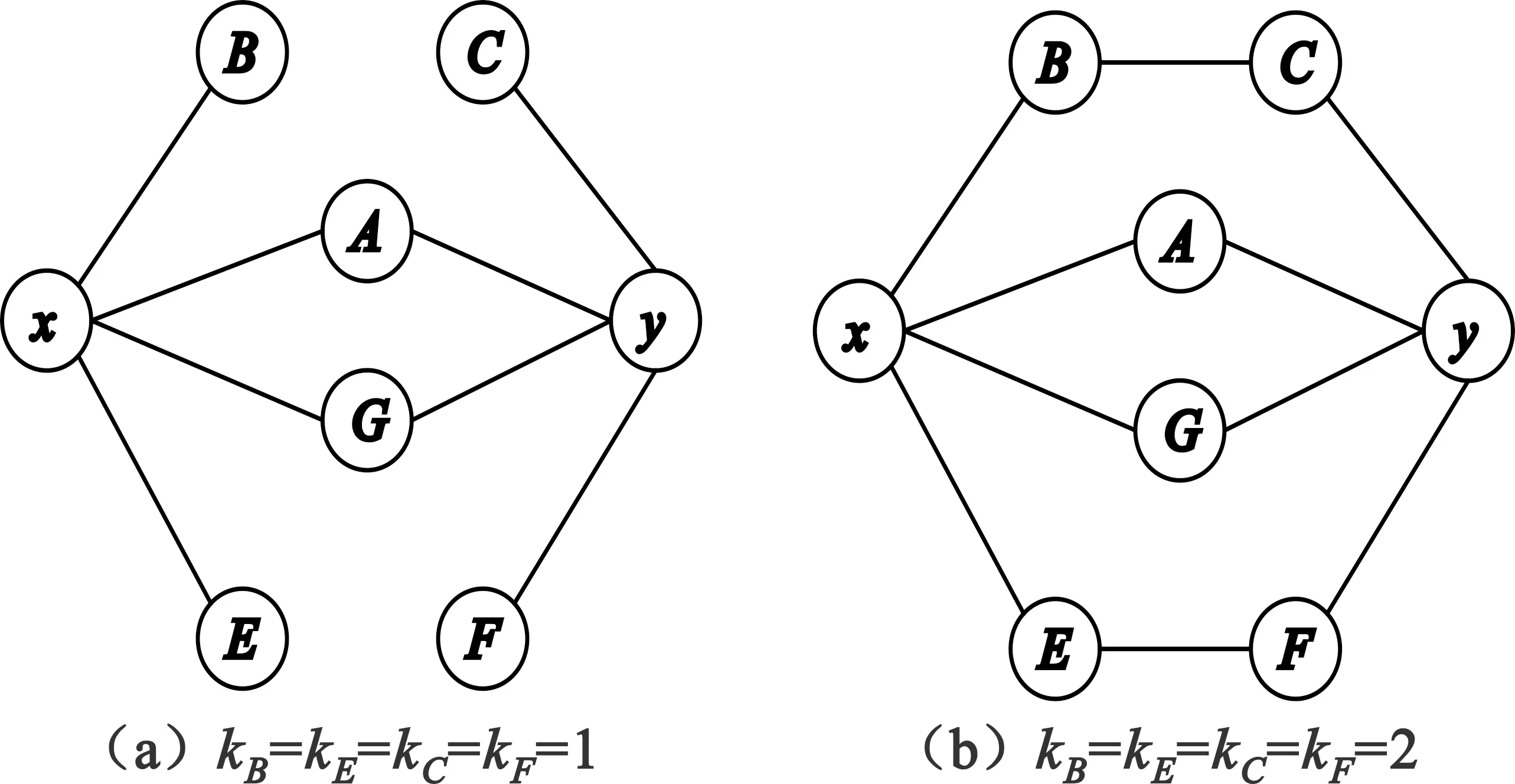
图1 两个复杂网络

根据基于节点的度和共同邻居数量的Salton、Sorensen、HDI、LHN和PA等局部相似性算法对节点对(x,y)的相似性进行计算。图1中节点对(x,y)的相似性分数是相同的，使用Salton算法计算节点对(x,y)的相似性分数都为0.5。这些算法无法预测图1中的节点x和节点y之间谁最有可能连接。

然而，根据公式(3)，可以得到图1(a)中被预测节点x和y的Psor指数为Psorx=Psory=2.08，图1(b)中节点x和y的Psor指数为Psorx=Psory=2.52。因此，图1(b)中被预测节点x和y的Psor指数要比图1(a)中被预测节点x和y的Psor指数大。可以看出，图1(b)中节点对(x,y)相比图1(a)节点对(x,y)更有可能连接。

综合考虑复杂网络的局部结构信息，本文提出了一种预测网络相似性的Psor相似性指标，其定义如下：

(4)

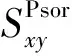
下面通过图1所示的两个复杂网络来验证Psor算法的可行性。根据公式(4)，分别计算图1(a)和图1(b)中节点x和节点y之间的相似性分数。

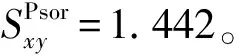
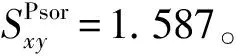
因此，按照本文提出的算法，图1(b)节点对(x,y)之间的相似性分数高于图1(a)节点对(x,y)之间的相似性分数，所以图1(b)中节点x和节点y更有可能连接，与事实吻合，说明本文提出的算法是可行的。

1.3 评价方法

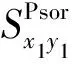
(5)

显然，当所有相似性分数都是随机独立生成时，那么AUC值应为0.5。AUC值超过0.5的部分说明了链路预测算法在多数水平程度上比随机选择准确，也表明AUC的值越大，链路预测算法的预测效果越好。

1.4 Psor算法流程

Psor算法流程如图2所示。

图2 Psor算法流程图

具体描述如下：

输入：无权无向预测网络边的列表linklist。

输出：相似性矩阵SIM，评价指标AUC的值。

开始：

(1)通过将导入的边转换成稀疏矩阵，然后删除自环，使得矩阵对角元为0，然后将矩阵转化成三角阵，最后再将三角阵通过转置转化成对称矩阵，转换结束后得到网络的邻接矩阵；

(2)然后确定测试集边的数目，将网络(邻接矩阵)中所有的边找出来，为每条边设置标志位，判断是否能删除，若选择的边可删除，则将之放入测试集中，依次将测试集中的边选取完毕，最终返回训练集和测试集；

(3)由邻接矩阵，获取预测节点的度、共同邻居数量以及其邻居节点的度，然后根据公式(3)计算预测节点的Psor指数；

(4)根据Psor相似性指标公式，求得最终的相似性矩阵SIM；

(5)根据相似性矩阵，取出测试集和不存在边集合的相似性度值进行比较，最终使用AUC计算公式(5)得到Psor算法的AUC值。

结束

2 实验结果与分析

本文运用Matlab工具实现对链路预测算法的仿真，选取常用的评价指标AUC作为预测效果。实验时，独立重复实验100次，计算100次AUC的平均值作为实验的最终结果。

2.1 实验数据集

为了验证所提算法的有效性，本文通过选取不同领域的网络作为测试数据集，所涉及的实验数据都来源于真实网络，真实网络的实验数据可以从www.linkprediction.org网站下载。下载的数据集首先要经过预处理，将有向链接更改为无向链接，并删除自循环和多链接来确保网络的不加权和无向。本文采用的5个典型的真实网络数据如下:

(1)金融市场网络(FINC)，节点表示金融中心名称，边表示各金融中心的交易，该网络共有89个节点和150条边；

(2)美国航空交通网络(USAir)，网络中的节点表示不同的机场，边表示机场之间有直飞航线，该网络共有332个节点和2 126条边;

(3)蛋白质相互作用网络(Yeast)，节点代表蛋白质，边代表两种蛋白质之间的代谢相互作用，该网络共有2 735个节点和11 693条边；

(4)政治家博客网络(Political Blogs，PB)，节点代表不同政治家的博客，边代表两个博客之间的超链接，该网络共有1 222个节点和16 714条边；

(5)线虫代谢网络(Metabolite)，节点是代谢物(例如蛋白质)，边缘是它们之间的相互作用，该网络有453个节点和2 040条边。

通过使用Gephi软件可将以上5种网络的数据集做简单分析，可以得到网络的平均度、网络的平均聚类系数、网络的平均路径长度、网络直径D、网络密度d(G)等网络基本拓扑特征，如表1所示。

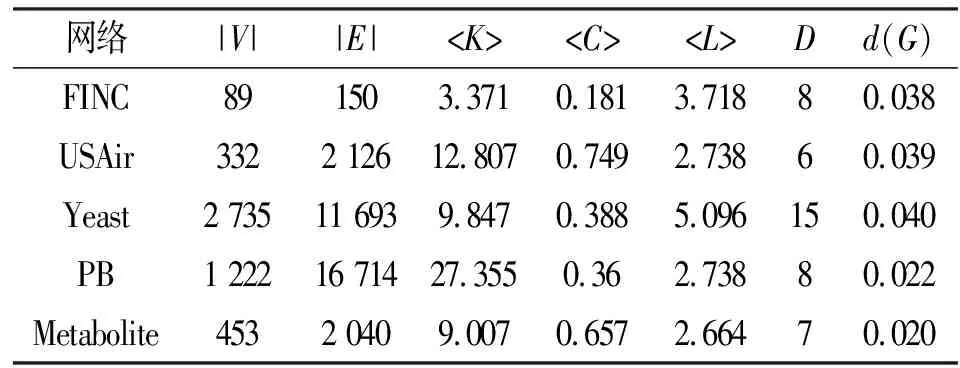
表1 数据集的网络特征

2.2 经典的相似性链路预测算法

为了说明本文所提算法的可行性，将选取几种经典的相似性链路预测算法作为基准算法。下面对几种经典的相似性链路预测算法进行介绍。

(1)Salton指标[18]。考虑了共同邻居和节点自身的度的影响，其定义为

(6)

(2)Sorensen指标[19]。考虑了共同邻居和节点自身的度的影响，认为节点间的相似性与这两个节点的度之和成反比，其定义为

(7)

(3)HDI指标[13]。考虑了共同邻居和节点自身的度的影响，其定义为

(8)

(4)LHN指标[20]。考虑了共同邻居和节点自身的度的影响,认为节点间相似性与这两个节点的度的乘积成反比，其定义为

(9)

(5)PA指标[21]。只考虑了节点自身的度，认为两节点的度的乘积越大，这两个节点越有可能连接，其定义为

(10)

(6)LHN-II指标[20]。它考虑的是所有的路径数，其表达式如下：

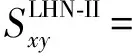
(11)

式中：δxy为Kroneckerδ函数，φ为取值小于1的参数，A为邻接矩阵，λ1为矩阵A的最大特征值，M为网络中边的总数。

(7)平均通勤时间(Average Commute Time，ACT)[22]。表示两节点之间平均需要走的步数，节点和节点的平均通勤时间为

n(x,y)=m(x,y)+m(y,x)。

通过求网络拉普拉斯矩阵L的伪逆L+获得其数值解，即

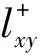
(12)

(8)基于转移偏好自洽相似性指标(Transferring Similarity Based on Preferential Attachment，TSPA)[23]。通过中间节点的传递特性，针对性克服了结构信息利用不充分的缺点，其定义为

(13)

2.3 与其他典型相似性算法对比

实验时，将网络数据集随机划分成一定比例的训练集和测试集。第一次实验将数据集划分为90%的训练集和10%的测试集，第二次实验将数据集划分为80%的训练集和20%的测试集，实验结果图3所示。

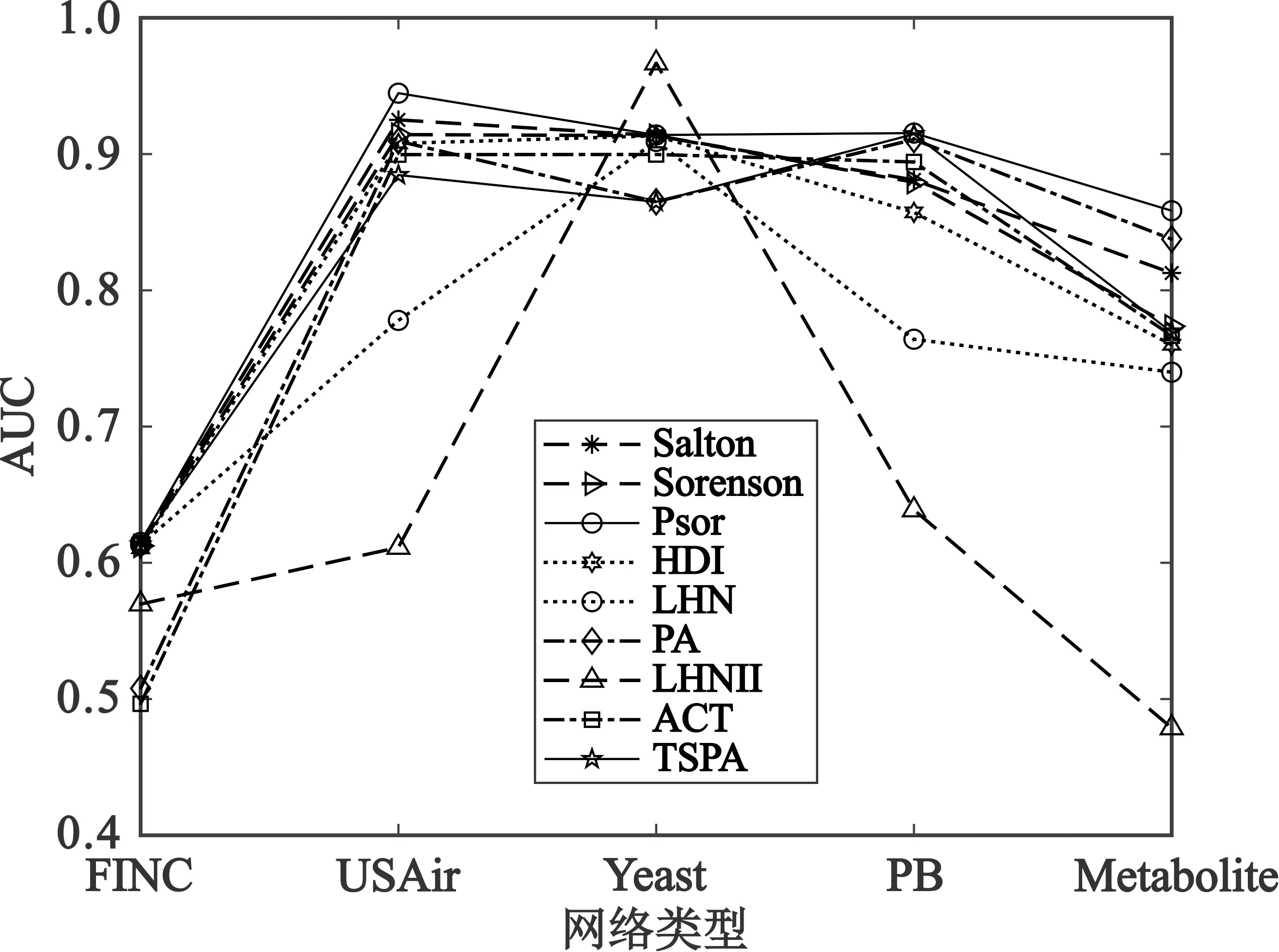
(a)测试集的比例为10%

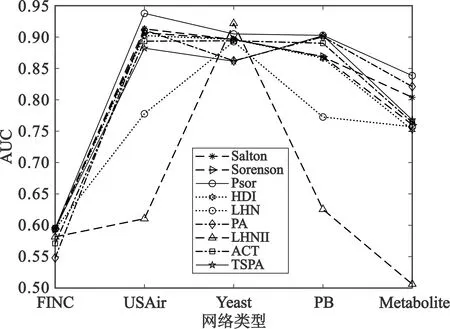
(b)测试集的比例为20%图3 不同测试集比例下不同网络中各相似性算法的AUC值

通过图3可以看出，在FINC、USAir、PB和Metabolite这四种网络中，Psor算法的AUC值明显高于其他8种链路预测算法的AUC值，也就是说所提的Psor算法在预测精度上可以获得更好的预测效果。在Yeast网络中，LHN-II算法能够获得最优的AUC值，而Psor算法的AUC值仅次于LHN-II算法，其他算法的AUC值都低于Psor算法的AUC值。此外还可以看出，在USAir、PB和Metabolite这三种网络中，LHN-II算法的预测精度最低，尤其在Metabolite网络中LHN-II算法的AUC低于0.5，这说明LHN-II算法不适合预测这个网络。因此，总体来看，Psor算法考虑邻居节点度的影响在网络中获取到的网络结构信息相对全面，链路预测性能与其他8种算法相比较优，预测精度得到了一定的提高。

表2是数据集分为90%的训练集和10%的测试集时，各相似性算法在不同网络中仿真出来的AUC结果。可以看出，在FINC、USAir、PB和Metabolite这四种网络中，相比其他8种算法，Psor算法的AUC值是最高的。在FINC网络中，Psor算法的AUC值相比其他8种算法至少提高了0.1%；在USAir网络中，Psor算法的AUC值相比其他8种算法至少提高了1.96%；在PB网络中，Psor算法的AUC值相比其他8种算法至少提高了0.47%；在Metabolite网络中，Psor算法的AUC值相比其他8种算法至少提高了2.09%。这说明Psor算法通过考虑节点自身的影响力和邻居节点的链接对预测的贡献，克服了传统算法只考虑共同邻居节点数目、节点自身的度以及节点间路径传输能力而未能完全挖掘路径信息的缺陷，有效提高了预测的精度。

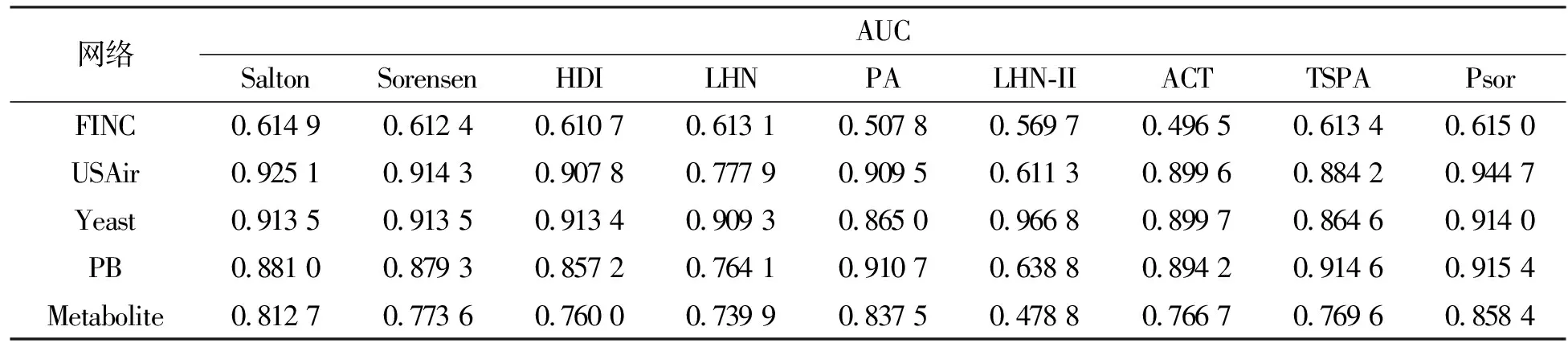
表2 训练集90%和测试集为10%时5个真实网络在不同算法下的AUC值

为综合衡量算法性能，将训练集的比例由90%改为80%，重新进行上述实验流程，得到各预测算法的AUC值如表3所示。类似地，可以看出在FINC、USAir、PB和Metabolite这四种网络中，相比其他8种算法，Psor算法的AUC值是最高的。以USAir网络为例，Psor算法较局部相似性Salton、Sorensen、HDI、LHN、PA算法分别提高了2.47%、3.08%、3.54%、16%和2.65%，较全局相似性LHN-II、ACT、TSPA算法分别提高了32.73%、4.43%和5.55%，说明邻居节点的度对节点对之间的相似性有一定的影响。Psor算法在预测时获得了更加全面的网络结构信息，从而有效提高了预测精度。

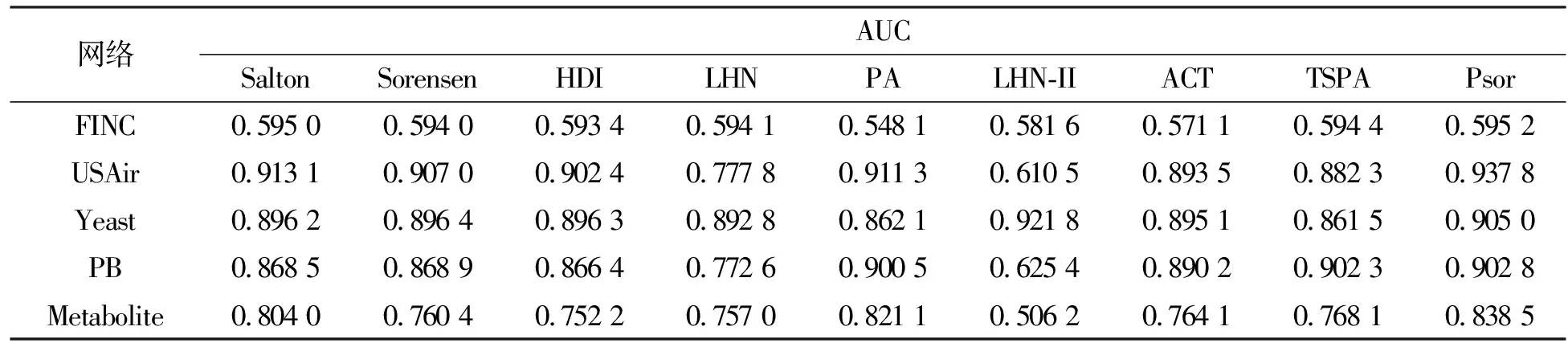
表3 训练集80%和测试集为20%时5个真实网络在不同算法下的AUC值

此外，在设计链路预测算法时，算法的效率也是必须考虑的。本文对比的算法中PA算法的时间复杂度为O(N2)；Salton、Sorensen、HDI、LHN算法都是基于共同邻居进行链路预测的，其时间复杂度为O(N3)；LHN-II指标、ACT指标和TSPA指标的时间复杂度为O(N3)。本文提出的Psor算法也是在共同邻居的基础上考虑度信息进行链路预测的，其时间复杂度为O(N3)。因此，可以看出Psor算法的时间复杂度相对没有增加。

综上所述，与Salton、Sorensen、HDI、LHN、PA、LHN-II、ACT和TSPA这8种经典链路预测算法相比较，本文所提的Psor算法在复杂度没有增加的情况下具有更好的预测效果。

3 结束语

本文在分析现有的链路预测算法特性的基础上提出了一种基于复杂网络的Psor链路预测算法。该算法充分考虑了复杂网络的局部结构信息，利用节点对的共同邻居、节点的度和节点的Psor指数等信息来对网络链路进行预测。通过在5个真实数据集中比较Psor算法与其他8种经典链路预测算法的AUC值来说明提出的算法对链接预测的效果。实验结果表明，Psor算法在预测效果上明显优于其他8种经典的链路预测相似性指标，可以提高链路预测的精确度，适用于一些网络中的节点连接预测。接下来的工作将会考虑有权、有向网络，将Psor算法应用到这种网络中。