基于GA-SVR算法的顺北区块固井质量预测

郑双进 程霖 龙震宇 刘洋 赫英状

1. 长江大学石油工程学院；2. 中国石油大学(北京)人工智能学院；3. 中国石油西南油气田分公司川东北气矿；4. 中国石化西北油田分公司工程技术研究院

固井是油气井建井的重要环节，也是保证油气井生产寿命的关键所在［1］。固井质量影响因素众多，受地层条件、井眼状况、流体性能、固井参数等多种因素综合作用，且各因素之间相互制约与关联，难以建立多因素条件下的固井质量预测解析模型［2-3］。国内外学者应用不同方法对影响固井质量的主要因素进行了相关性分析，初步建立了一些固井质量评价方法。Li Xue等将不同的测井评价方法有机结合起来，形成了适用于不同要求的固井质量评价体系，但评价结果受人为因素影响较大［4］；Market等模拟了套管在井中的随钻声波仪器响应，但未考虑在固井质量评价方面的应用价值［5］；Kinoshita等、Pistre等也进行了随钻声波定量评价固井质量的可行性探索［6］；Sun Zhicheng等运用模糊评判和灰色关联理论建立了固井质量多因素统计方法［7］；Zhu Yuxi等利用人工神经网络算法建立数学模型进行固井质量预测，应用结果表明，预测值与实际值还存在一定差距［8］；Ni Hongmei 等建立了基于人工神经网络的固井质量预测方法，预测精度较高，但耗时较长［9］。

近年来，SVR被证实是一种可靠的机器学习算法，它克服了人工神经网络的诸多缺点，因而在科学与工程的多个领域得到了大量应用［10］。基于西北油田顺北区块历史固井数据，在固井质量影响因素分析的基础上，建立并优化得到了基于GA-SVR算法的固井质量预测方法。

1 固井质量影响因素分析

西北油田顺北区块井深大，封固段长，井底温度高，环空间隙小，固井施工过程中易造成环空憋堵，引发井下漏失，水平井套管难以居中，顶替排量受限，固井质量难以保证。经多年经验总结及质量分析，固井质量主要影响因素有井斜角、狗腿度、井径扩大率、套管居中度、注浆返速、替浆返速及水泥浆接触时间：(1)井斜角较大情况下，套管居中不好，或套管在狗腿度较大井况下易贴边，岩屑及钻井液难以被有效驱离，同时易产生绕流影响固井质量；(2)注浆返速、替浆返速及水泥浆接触时间是影响顶替效率的关键，其直接影响固井流体对钻井液的驱替效率，进而影响固井质量；(3)井径扩大率直接影响注浆返速和替浆返速，间接影响固井质量。

2 支持向量机模型建立

支持向量机SVM(Support Vector Machines)的主要思想是结构风险最小化原则和统计学习理论VC维理论［11］。SVM算法在解决小样本、非线性回归模型中表现出优势，在很大程度上克服了“维数灾难”和“过学习”等问题［12］。

以二分类为例，设样本集合为{(x1,y1),(x2,y2),···,(xi,yi)},(i=1,2,···,m)。在样本空间，最优分界面线性方程为

式中，ω为法向量； ωT为 法向量的转置；b为位移项。要使超平面(ω,b)能对训练样本正常分类，则

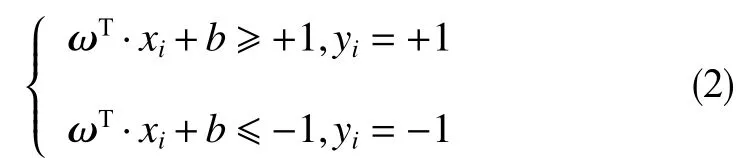
y(x)=sgn(ωT·x+b)

由此可得决策函数 ，为了最大化间隔，可化为二次规划问题

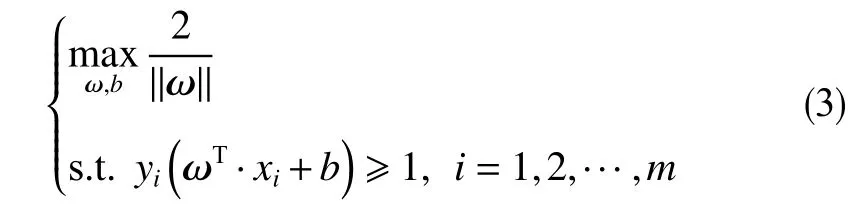
式中，s .t.是subject to的缩写，意为受约束。引入Lagrange函数

求其对偶问题

解出α，进而求出ω与b即可得到模型为

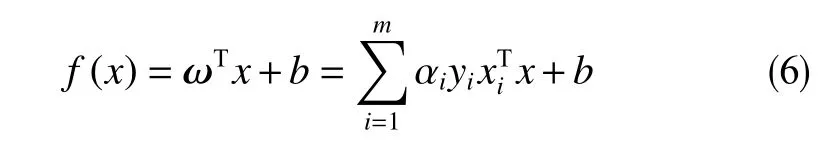
其中，αi满足卡罗需-库恩-塔克条件KKT(Karush-Kuhn-Tucker)

由于一些点出现在2条线的间隔内部，不满足函数间隔的约束条件，故引入松弛变量εi用以表征该样本不满足约束的程度，则有

式中，εi为松弛变量；C为惩罚系数，C＞0。

若遇线性不可分情况，可将样本映射到一个更高维的特征空间，使其在这个特征空间内线性可分。在特征空间中划分最优超平面对应模型表示为

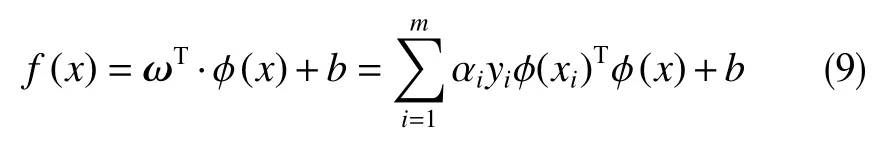
最后，可采用“核技巧”，引入核函数避免式(9)中的维数灾难，常用核函数有线性、多项式和高斯函数(也称为径向基函数RBF)，最终得到SVM非线性回归模型的表达式为

通过研究可知，基于SVM模型的固井质量预测方法，实质上是利用SVM中的算法SVR(Support Vector Regression)构建一个误差范围，将落在误差范围内的预测值视为预测正确，与SVM模型思路(到“超平面”最近样本点的间隔最大，如图1所示)不同，SVR则是要使到“超平面”最远样本点的间隔最小。

图1 最优超平面示意图Fig. 1 Sketch of optimal hyperplane

3 固井质量预测模型

在模型训练中，笔者从顺北油田某井获取了48段历史固井数据，每段包括固井质量(CBL声幅值)及其影响因素：井斜、狗腿度、井径扩大率、套管居中度、注浆平均返速、替浆平均返速及水泥浆接触时间，各种因素之间相互作用、相互抑制或相互依赖，通过代入模型进行训练后评估，得到了准确的固井质量预测模型。

3.1 SVR算法建模

将48组原始数据使用标准化方法中的maxmin方法进行处理，防止原数据集的数据维度过大对预测结果造成影响，如式(11)所示。采用均方根误差(RMSE)和平均相对误差(MRE)对固井质量的预测结果进行评价，以此验证模型的准确性，如式(12)、式(13)所示。

式中，oi为固井质量的真实值；pi为固井质量的预测值；n为预测数据的组数。

以井斜、狗腿度、井径扩大率、套管居中度、注浆平均返速、替浆平均返速、水泥浆接触时间为输入量，以固井质量为输出量，基于SVR建立固井质量预测模型。

由Python中的Pandas方法从原始数据集中划分出建立模型所需要的训练数据以及评估模型精度所需的测试数据，划分比例为5∶1，将其中的40组作为训练数据，剩下的8组作为预测数据。处理后的数据利用Python中的Sklearn方法，使用默认的SVR模型进行建模，其中，核函数类型Kernel为Rbf核函数，正则化参数Lambda设为1，核函数参数Gamma设为1/7。划分的测试集及其预测结果的相对误差见表1，预测时间小于1 s。由表1可见，SVR预测固井质量与实际固井质量的最大相对误差为23.37%，最小相对误差1.03%。通过计算得出，平均相对误差MRE为9.80%，均方根误差RMSE为2.851，可对SVR参数进行优化，以期得到精度更高的模型。

表1 测试集及模型预测评价Table 1 Test set and model prediction evaluation

3.2 模型优化

对于SVR算法而言，其惩罚系数C和核函数参数g的选择将直接影响到模型预测误差，前人也不断进行SVR回归研究［13］，对SVR参数的合理设置提出了一些意见，但仍然存在很多矛盾。通过实际研究，为缩小SVR预测误差，首先使用网格搜索法［14］、贝叶斯算法［15］、遗传算法［16］对参数C和g进行寻优，然后再用优化后的SVR算法对相关数据进行训练和预测。研究中由Python指定Rbf作为核函数，指定惩罚系数C的范围为0.1~100，核函数参数g的范围为0.01~1。

3.2.1 网格搜索法优化SVR模型(GS-SVR)

网格搜索法(Grid Search, GS)［17］是全局优化算法中最简易的方法之一，是一种通过遍历给定的参数组合来优化模型表现的学习方法，其原理是先确定模型搜索范围，将待搜索参数的可能取值按照一定步长进行分离，生成“网格”，然后将对每个网格节点进行逐次搜索，运用目标函数进行判断，根据目标函数值调整搜索范围和步长，直至搜索出最优解。网格搜索法的优化流程如图2所示。

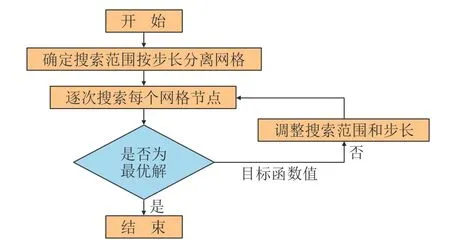
图2 网格搜索法流程Fig. 2 Process of grid search method

3.2.2 贝叶斯算法优化SVR模型(BOA-SVR)

贝叶斯优化算法(Bayesian Optimization Algori thm, BOA)［18］的思路主要是根据先验知识对每次采样点进行测试并更新先验分布，最终找出全局最优值。假设已经存在一个样本S，其中包括t个参数组和对应目标函数值，首先通过高斯过程计算其后验概率分布Dt，即联合正态分布，然后选择函数a(x|Dt)，采集一个新参数值xt+1，使其满足式(14)

即在分布中Dt取值能使新的估计目标函数值ft+1(x)与 当前最大目标函数值fbest差值的期望最大，然后用这一新参数值计算新的实际目标函数值，并相应更新高斯过程，得到新的后验分布Dt，之后重复前述过程不断进行优化，直到满足停止条件。贝叶斯优化算法的优化流程如图3所示。

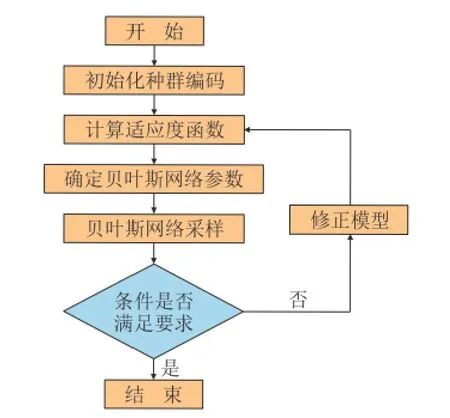
图3 贝叶斯优化算法流程Fig. 3 Process of Bayesian optimization algorithm

利用网格搜索法优化SVR模型，优化后的最优参数为惩罚系数C=25.10，核函数参数g=0.13，优化结果及模型评价见表2，预测时间为44.8 s。由表2数据计算可得，GS-SVR预测固井质量与实际固井质量的平均相对误差MSE为8.46%，均方根误差RMSE为2.653，有一定的优化效果。

表2 网格搜索法优化结果及模型评价Table 2 Optimization result and model evaluation of grid search method

利用贝叶斯算法优化SVR模型，优化后的最优参数为惩罚系数C=47.38，核函数参数g=0.07，优化结果及模型评价见表3，预测时间为19.8 s。由表3数据计算得出，BOA-SVR预测固井质量与实际固井质量的平均相对误差MSE为8.00%，均方根误差RMSE为2.533，优化效果较好。

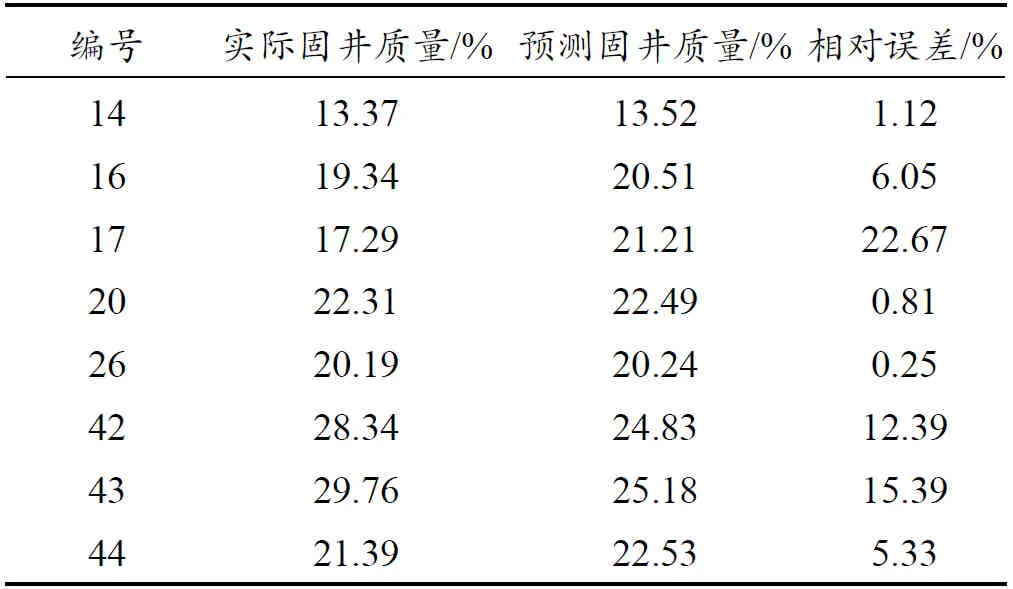
表3 贝叶斯算法优化结果及模型评价Table 3 Optimization result and model evaluation of Bayesian algorithm

3.2.3 遗传算法优化SVR模型(GA-SVR)

遗传算法(Genetic Algorithm, GA)［19］是基于自然界遗传机制和生物进化论的一种高效随机搜索和优化方法。GA具有全局优化性能，运用在SVM中能够寻找参数C和g最合适的值，使得SVM达到最优配置，从而更加准确地预测固井质量。遗传算法的优化流程如图4所示。

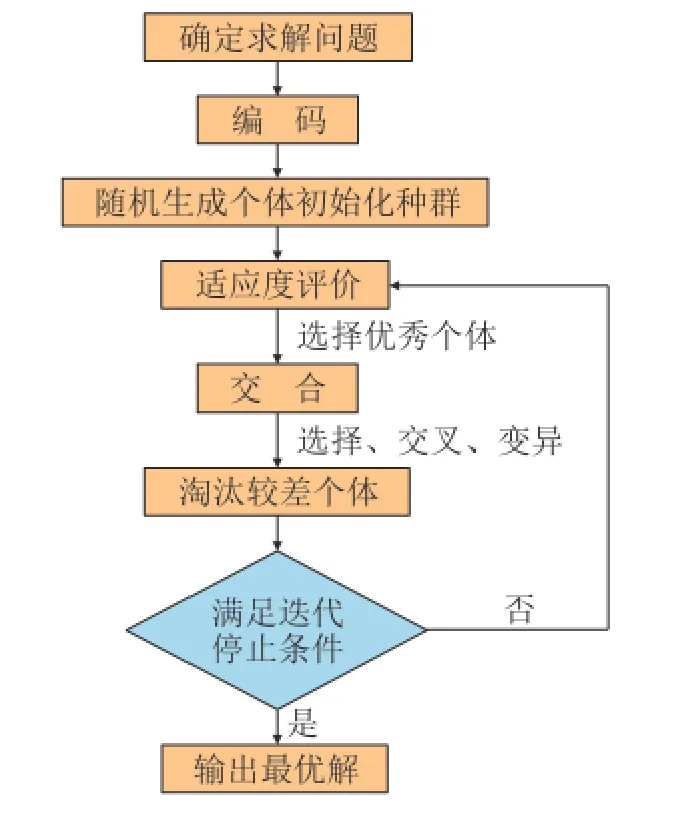
图4 遗传算法流程Fig. 4 Process of genetic algorithm

在Python中运行GA-SVR代码，利用遗传算法优化SVR模型，优化后的最优参数为惩罚系数C=85.08，核函数参数g=0.02，优化结果及模型评价见表4，预测时间为 36.3 s。由表4数据计算得出，利用GA优化后构建的SVR模型比SVR、GS-SVR和BOA-SVR预测精度更高，平均相对误差MSE为7.30%，均方根误差RMSE为2.318，优化效果最好。

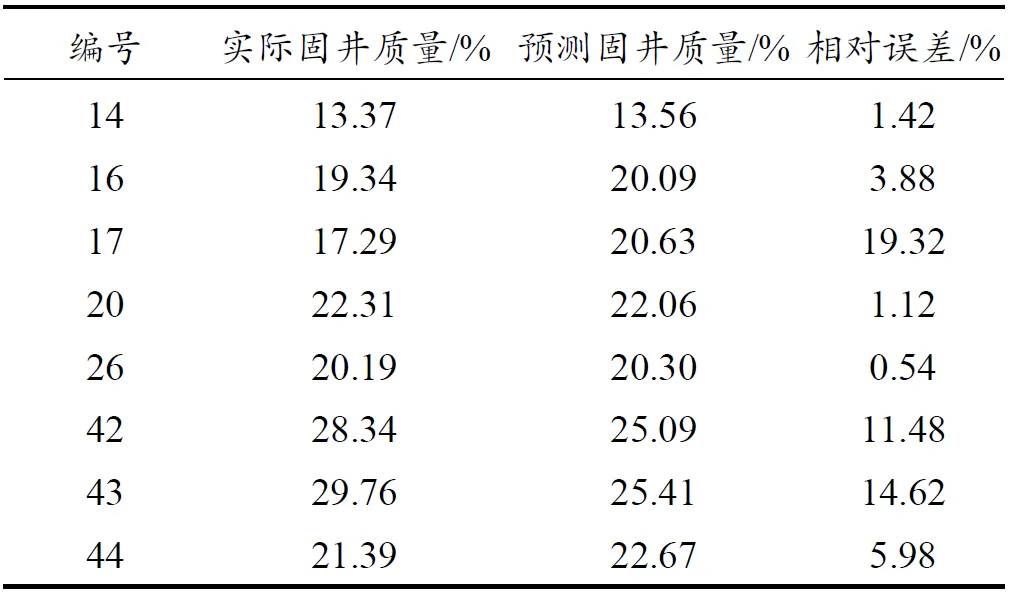
表4 遗传算法的优化结果及模型评价Table 4 Optimization result and model evaluation of genetic algorithm

3.3 固井质量预测结果分析

基于SVR建立了固井质量预测算法，并对SVR的惩罚系数C和核函数参数g进行优化，参数优选过程使用Python编程进行，采用GA、GS、BOA共3种参数优选法。4种算法预测结果对比见表5。由表5可知，GA-SVR算法预测结果的平均相对误差为7.30%，均方根误差RMSE为2.318，远小于SVR、GS-SVR、BOA-SVR，表明该算法更加适合于固井质量预测，根据表5的时间可分析得出，GA-SVR算法消耗时间较长，说明该算法相比于SVR、BOA-SVR模型更加复杂，考虑因素更全面。

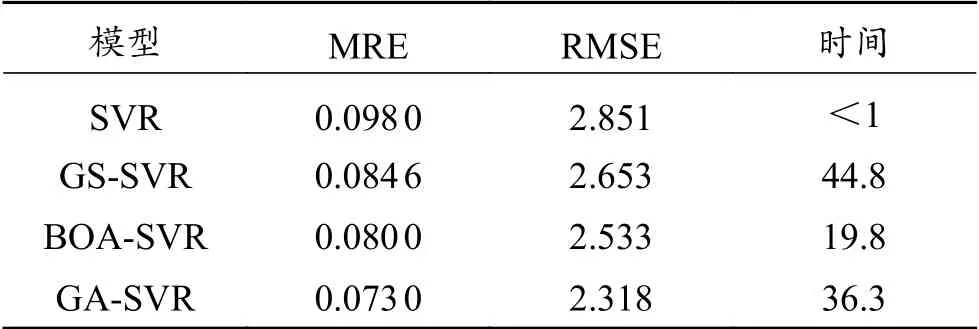
表5 模型优化前后评价Table 5 Model evaluation before and after the optimization

4 实例验证

实例验证采用皮尔逊相关系数法，它是一种度量2个变量X和Y之间相关程度的方法，X和Y之间的皮尔逊相关系数定义为两者的协方差和标准差的商，如式(15)。皮尔逊相关系数是一个介于−1和1之间的值。其中，1表示变量完全正相关，0表示无关，−1表示完全负相关［20］。

式(15)定义了总体相关系数，估算样本的协方差和标准差，计算方法为顺北区块某井完钻井深8 725.00 m，最大井斜角86.01°，最大全角变化率18.38°/30 m，最大井径扩大率12%，钻井液密度1.68 g/cm3，塑性黏度36 m Pa·s。针对该井Ø139.7 mm尾管固井，由于采用无接箍镦粗直连扣套管，不能安放扶正器，套管紧贴下部井壁，居中度基本为0；设计1.05 g/cm3的驱油冲洗液7.0 m3，1.75 g/cm3加重隔离液4.0 m3，1.88 g/cm3水泥浆11.0 m3，设计注替排量为0.6~0.8 m3/min。该井整个封固段CBL测井声幅值在10%~30%之间，其中7 850~8 000 m固井质量为优秀。将该井固井数据运用GA-SVR算法进行固井质量预测，预测值与实际值对比如图5所示，皮尔逊相关系数r=0.9781，GA-SVR算法预测值与实际固井质量值之间具有很好的相关性。

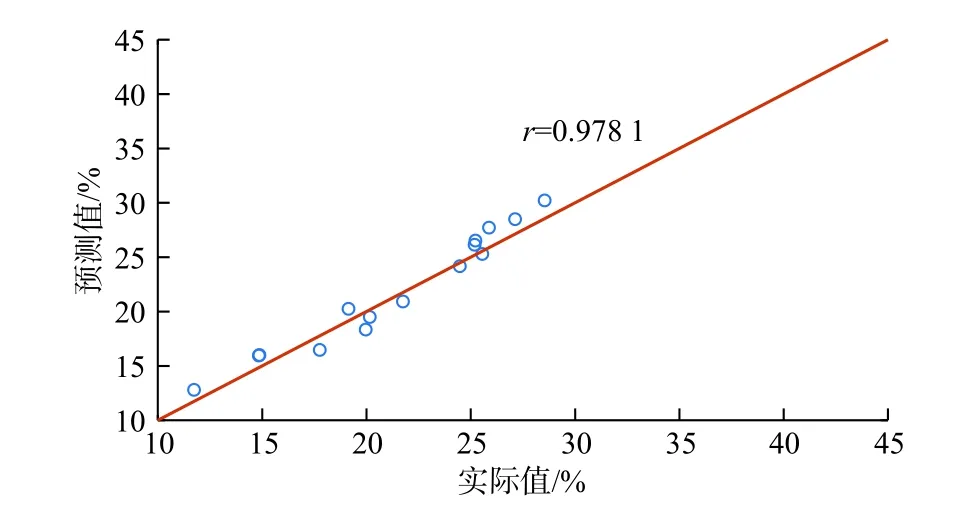
图5 固井质量实际值与预测值的相关性对比Fig. 5 Correlation between actual value and predicted value of cementing quality

为了进一步分析GA-SVR模型预测值与固井质量实际值之间的偏差大小，针对模型预测结果的相对误差进行了分析，分析结果见表6。第6组数据的预测结果相对误差最大，为9.16%；第1组数据的预测结果相对误差最小，为1.27%，大部分组数的预测误差集中在5.5%附近，平均相对误差MRE为5.27%，平均均方根误差RMSE为1.166。研究结果表明，GA-SV算法预测值与固井质量实际值的匹配程度较高，误差较小，可用于顺北区块固井质量预测。

表6 GA-SVR模型预测固井质量相对误差Table 6 Relative error of cementing quality predicted by GA-SVR model

5 结论

(1)固井质量受地层条件、井眼状况、流体性能、固井参数等多种因素综合作用，并且各因素之间相互制约与关联，基于固井数据量级及特征建立了基于支持向量回归(SVR)的固井质量预测模型。

(2)运用网格搜索法(GS)、贝叶斯优化算法(BOA)、遗传算法(GA)进行优化，结合顺北区块历史固井数据，分别运用SVR、GS-SVR、BOA-SVR、GA-SVR 共4种算法对固井质量进行预测，预测结果表明GA-SVR算法精度较高，可用于顺北区块固井质量预测，有助于该区块固井方案优化。

(3)在使用SVR算法的过程中，惩罚系数C、核函数系数g的选择会对数据学习和预测结果产生较大的影响，如何选择系数是固井质量预测的关键。