基于热传导方程的最佳炉温曲线研究

关 聪，陈 英，王 哲

（广西民族大学，广西 南宁 530000）

1 问题背景

回焊炉是集成电路板等电子产品生产的重要工具之一。在生产过程中电子制造行业中印刷电路板（PCB）回流焊工艺是SMT技术重要的一环，回流焊温度曲线会实时记录焊接过程温度的变化。在现实的生产过程中，不少企业认为确保回流焊炉处于良好的制程状态是质量控制的关键，因此需要对回焊炉温度曲线进行持续的测量检查，所以炉温曲线的研究可以保证焊接质量，降低测试成本，确保回流焊炉具有优良的制程能力。回焊炉截面示意图如图1所示。

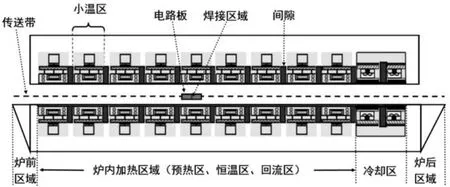
图1 回焊炉截面示意图

2 目标问题

本文旨在对工具机理模型进行分析研究，为有效测量各温区温度值，并确定最优传送带传送速度，建立温度变化规律数学模型，从而解决炉温曲线相应问题。

问题一：在给定各温区温度设定值条件下，计算焊接区域中心温度变化情况，并画出相应炉温曲线。制程界限如表1所示。

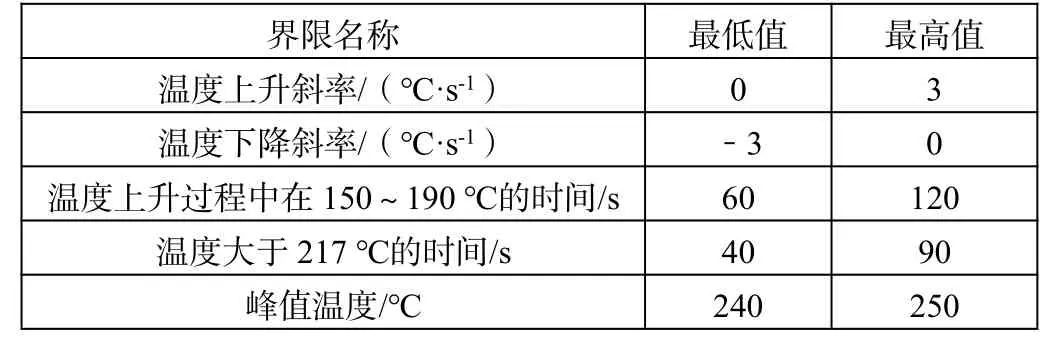
表1 制程界限

问题二：以峰值温度为中心线的两侧超过217℃的炉温曲线应尽量对称，结合给出的传送带最大过炉速度，画出最优曲线、各温区设定的温度及传送带过炉温度及相应指标。

3 模型的假设

模型的假设如下：①集成电路板的边界长l=2.5 cm，且两端边界相等；②两块相等温度的集成电路板边界与间隙的最低温度差值ΔT=170℃；③过炉速度匀速稳定，不存在突变；④受传热影响，相同温度的两块小温区之间间隙中心温度低于5℃；⑤假设受传热影响，第一个边界略高于室温为26℃；⑥不考虑电子元件材料等对温度测量和焊接的影响；⑦假设更改小温区温度值后，加热温度最终趋于稳态；⑧假设过炉过程中，电路板表面加热温度即为小温区温度；⑨假设调整小温区非边界温度都能精确到设定值；⑩假设在调节温区温度时，原先速度始终为该状态下最大过炉速度。

4 模型的建立与求解

4.1 模型的建立

4.1.1 稳态热传导过程分析

4.1.1.1 导热微分方程

满足直角坐标系一维、稳态、常物性、无内热源、第一边界条件下控制方程为：

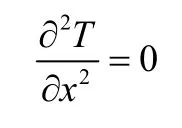
将控制方程积分计算得出通解：

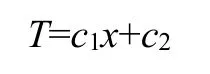
4.1.1.2 回焊炉内热传导稳态温度分布分析

回归本题中，假设将小温区看成一有限长的细状热源，回焊炉内有以下情况的稳态热传导过程：炉前区域与第一小温区之间、温度相等的温区之间、温度由低到高的两各温区之间、温度由高到低的温区之间。

假设刚进入炉前初始边界温度为T00，在每一段有限长热源的两端靠近端点处都取一相同距离l位置的温度，靠近左端点的温度为Ti1，靠近右端点的位置为Ti2。x为小温区与起始点距离，假设小温区间隙为5 cm。

炉内加热过程如图2所示。

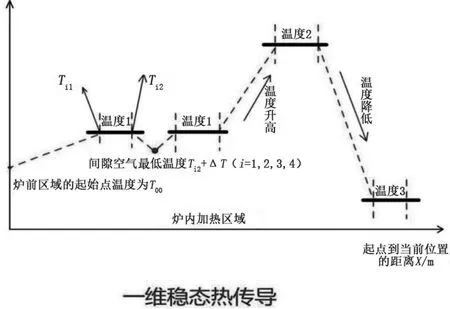
图2 炉内加热过程

根据图2，小温区有以下四个一维稳态热传导过程：炉前区域起始温度分布、温度相等的相邻小温区区域的温度分布、温度升高的相邻小温区区域的温度分布、温度降低的相邻小温区区域的温度分布。

过程一：炉前区域与小温区区域温度分布。

研究物体内温度分布（温度分布为线性分布）：

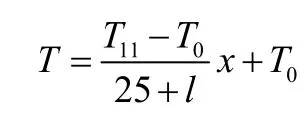
过程二：温度相等的相邻小温区区域的温度分布。

根据热传导过程，相同温度小温区与间隙处于热平衡状态，小温区释放能量，间隙吸收能量，则间隙中点必然存在一个温度最低点，即为间隙中点，间隙长度为5 cm，间隙离中点距离为2.5 cm，设该点与温区的温度差ΔT=5℃。

利用导热方程通解算出平衡状态下温度分布：

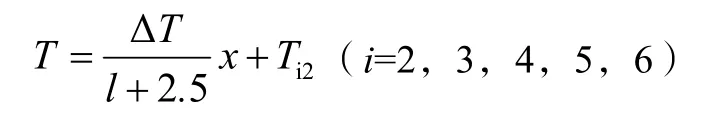
过程三：温度升高的相邻小温区区域的温度分布。

根据热传导过程，低温小温区与高温小温区区域存在温度差，同时相邻小温区区域会达到热平衡稳态。

边界条件为：

代入导热方程通解算出平衡状态下温度分布：

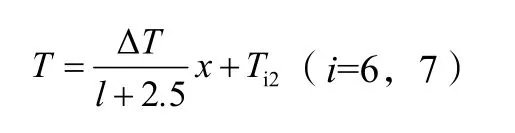
过程四：温度降低的相邻小温区区域的温度分布。

同过程三，高温小温区与低温小温区区域存在温度差，同时相邻小温区区域会达到热平衡稳态。边界条件为：

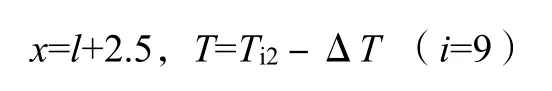
代入导热方程通解算出平衡状态下温度分布：

4.1.2 非稳态热传导过程分析

已知非稳态有内热源的导热微分方程：

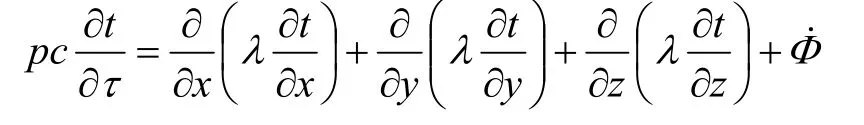
由于焊接点的厚度为0.15 mm，可忽略不计，则电路板焊接区域温度在统一瞬间各点温度基本相等，即t仅是的一元函数，与坐标x、y、z无关，即：

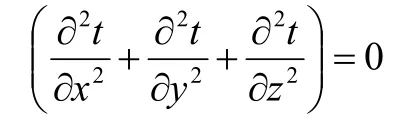
从而：

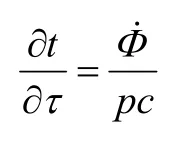
界面上交换的热量应折算成整个物体的体积热源，即-ΦV=Ah（T-T0）。

电路板进入回焊炉内时到达某一点时初始温度与加热温度的关系式为：

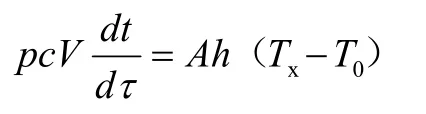
整理一下得出以下关系式：

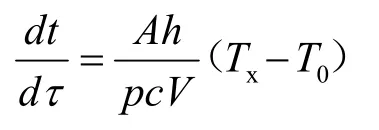
已知印刷电路板（PCB）体积，受热表面积A，物性参数ρ、c、λ，热交换系数h均为常数，令：

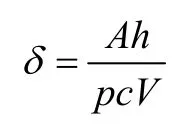
一维非稳态导热方程变为：

4.2 模型的求解

4.2.1 问题一的求解

首先，分析整个过程可以得出：炉内传送过程为稳态热传导过程，集成电路板的瞬时加热过程为非稳态的热传导过程。假设传送带过炉速度为78 cm/min，各温区温度的设定值分别为173℃（小温区1～5）、198℃（小温区6）、230℃（小温区7）和257℃（小温区8～9）。

其次，将求解过程分为三个步骤：①将附件中的温度曲线和加热集成电路板的瞬时温度与电路板的位置关系图做出比较关系图；②考虑所有过程的热量损失问题，将热传导的两个过程分别进行数值计算；③最后根据不断调试的热量参数h，得到调试后的炉温曲线图。

解：根据稳态导热方程，已经画出焊接区域的大概温度曲线，如图3所示。

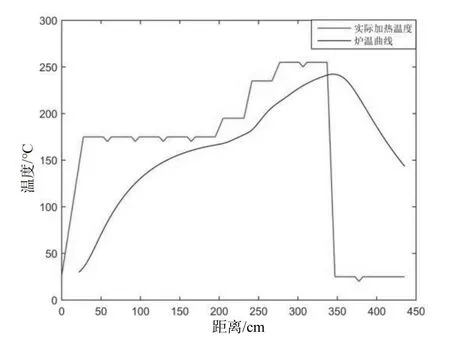
图3 焊接区域的大概温度曲线

结合一维非稳态导热方程与Matlab，根据题中所给的各参数的数值：175℃（小温区1～5）、195℃（小温区7）、255℃（小温区8～9）及25℃（小温区10～11），传送带的过炉速度为70 cm/min，由于δ的数值很难计算，可以先假设δ=0.006，可以看出当电路板位于0～25 cm，稳态温度曲线与炉温曲线的拟合程度最高。

同理，可以得出不同位置范围内实现稳态温度曲线与炉温曲线拟合程度最高的一维非稳态导热方程系数：

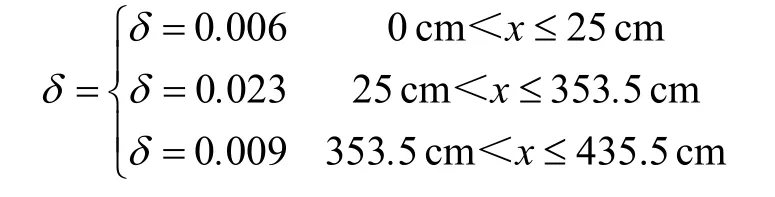
通过改变不同位置段的δ值，将找到拟合程度最高的稳态温度曲线，如图4所示。

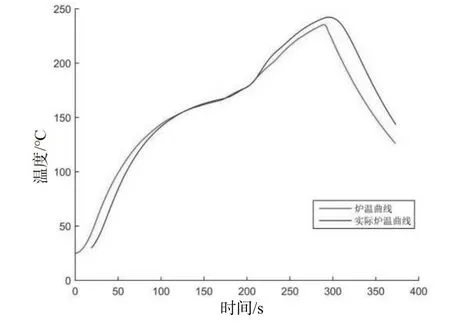
图4 稳态温度曲线

已知电路板（PCB）在进入回焊炉之前的温度为T0=25℃，假设炉前区域的起始温度取T00=26℃，炉前区域的起始点为研究起始点，电路板上焊接区域中心每隔0.1 s之后，移动的位移Δx=v·Δt=78 cm/min×0.1 s=0.013 cm，对照稳态温度曲线找出电路板移动Δx后的位置的初始温度T（x），则Tx-T0为始末温度差温度，再结合一维非稳态导热方程，可以算出加热温度ΔT，从而解得这一位置焊接区域中心的温度，该温度也为下一位置的焊接区域中心未加热前的初始温度；利用迭代方法，从而求出每隔0.1 s后对应位置上焊接区域中心的温度。

根据问题一中所给参数的数值，变换各温曲温度的设定值分别为182℃（小温区1～5）、198℃（小温区6）、239℃（小温区7）和257℃（小温区8～9），画出炉温曲线。已知传送带过炉速度为78 cm/min，炉温曲线再结合一维非稳态导热方程，运用迭代法，计算得出每隔0.1 s后对应位置上焊接区域中心的温度，结合Matlab画出焊接区域中心的温度变化曲线。分别计算小温区3、6、7中点及小温区8结束处距炉前区域起始点的位移xi（i=3，6，7，8），由算出电路板到达对应位置所用的时间，再根据焊接区域中心的温度变化曲线找出小温区3、6、7中点及小温区8结束处焊接区域中心的温度，结果如表2和图5所示。

表2 焊接区域中心的温度

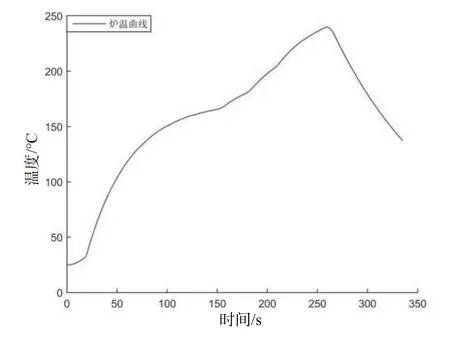
图5 焊接区域中心的温度变化图

4.2.2 问题二的求解

探究焊接过程，在满足制程界限的情况下，要使以峰值温度为中心线的两侧超过217℃的炉温曲线应尽量对称，需要算出合适的传送带过炉速度v和各温区设定的温度T有关，因此需要讨论以下两种情况。假设各温区温度的设定值分别为182℃（小温区1～5）、203℃（小温区6）、237℃（小温区7）、254℃（小温区8～9），传送带最大过炉速度v=79 cm/min。

第一种：探究同一次加热情况下不同温度对炉温温度的影响。

为了探究温度的影响，采用控制变量法控制各温区的温度不变，恒定设置为182℃（小温区1～5）、203℃（小温区6）、237℃（小温区7）、254℃（小温区8～9），已知传送带的过炉速度调节范围为65～100 cm/min，假设速度步长为0.5 cm/min，调节温度大小。此时根据问题一求解方法结合Matlab，可以得到此时的炉温曲线，从而得到炉温峰值的温度Tmax以及焊接区域中心到达峰值时刻tmax；再利用炉温曲线上217℃对应的点得出升温到217℃的时间ti1以及降温到217℃的时间ti2，则算出升温到217℃的点到炉温峰值经历的时间tmax-ti1以及炉温峰值降温到217℃的点经历的时间ti2-tmax，算出炉温峰值到左右217℃温度的点之间的时间偏差Δti1=（tmax-ti1）-（ti2-tmax），则位时间偏差越接近于0，图像越趋于对称。其中i=1，2，3，…，70。

传送带的过炉速度与时间偏差关系如图6所示。

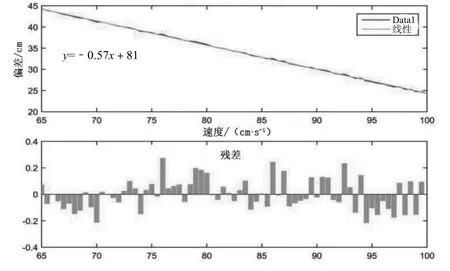
图6 传送带的过炉速度与时间偏差关系

可以直观看出过炉速度越大，偏差值越小，所以要取符合条件的最大速度，即最大传送带过炉速度v=79 cm/min。

第二种：探究同一传送带速度下改变小温区7、8的温度对炉值温度的影响。

在已知的允许的最大传送带过炉速度下，改变温区7、8的温度T7i、T8i，其他温区的温度为了方便计算，设置成问题二中的所给温度。根据问题一求解方法结合Matlab，可以得到此时的炉温曲线，类比第一种情况的方法，算出时间偏差Δt2i。

以温区7为x轴，温区8为y轴，时间偏差Δx为z轴，画出三者变量的散点关系图，如图7所示。

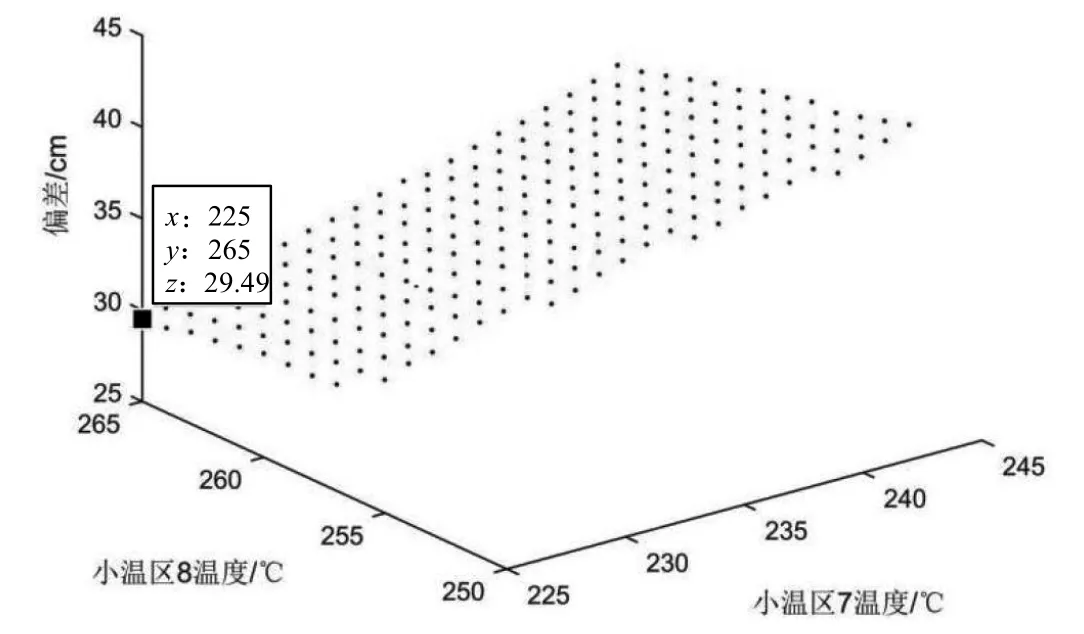
图7 散点关系图

由图7可以直观地看出当温区8温度最高即T8=257℃，温区7温度最低即T7=225℃的情况下时间偏差最小，该炉温曲线更符合题中所给要求的最优情况。该题的指标为在不同传送带速度和各温区的不同温度下升温到217℃的点到炉温峰值经历的时间tmax-ti1以及炉温峰值降温到217℃的点经历的时间ti2-tmax的时间偏差，时间偏差越小，则越趋于对称。

根据上述分析，将各温区温度的设定值分别为182℃（小温区1～5）、203℃（小温区6）、225℃（小温区7）、257℃（小温区8～9）。符合题意要求下允许的最大传送带过炉速度为v=79 cm/min时，区域最接近对称，根据参数画出如下炉温曲线，如图8所示。

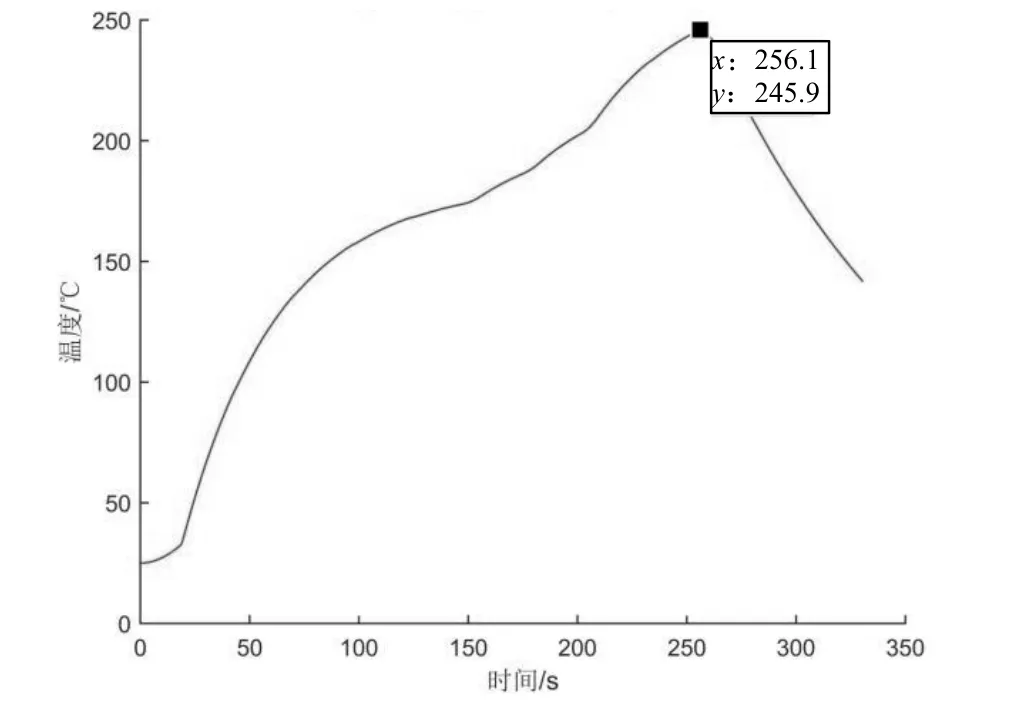
图8 焊接区域最接近对称的炉温曲线图

此时曲线峰值温度为245.9℃。

5 模型的应用和推广

模型一中运用包含稳态热传导过程与非稳态热传导过程。稳态热传导模型运用十分广泛。本文稳态热传导过程中主要运用一维热传导方程。该模型在生活中运用有密封材料的放热、高温作业衣物隔热、一维稳态传热过程类电流求解方法的讨论、多层组件常压隔热性能实验研究、纯金属型连铸模型试验研究，等等。

本题的整体研究方向为回焊炉炉温曲线研究，旨在提高焊接工艺技术，延长机器使用，保障企业产品质量，对同物理原理的机器研究具有同样适用性。