船舶压力注水管道水锤及防护措施研究
雷威,程舟济,潘永军,彭贝
(武汉第二船舶设计研究所,湖北 武汉 430064)
在船舶压力注水管道中,由于海水流动速度的突然变化导致管道中产生急剧的压力交替变化的水力撞击现象,称为水锤。就本质而言,水锤就是管道瞬变流动中的一种压力波,它的产生是由于管道某处的流速发生了急剧改变,从而导致该处的压力产生突然跃升或下跌,这个压力的瞬变波就是水锤。在船舶压力注水管道注水过程中,压力管道中的阀门快速关闭时,由于水锤现象,管道内的海水压力会迅速变化,可能上升至正常工作时压力的几倍甚至是几十倍。
由于船舶压力注水系统管道长、水力条件复杂、阀门启闭频繁,水锤在船舶压力注水管道中产生的振动不仅会对管道产生危害,当管道内产生周期性的压力波动时,将有可能引发系统的共振,对系统和设备的稳定构成了严重的威胁。曹云等研究了管道中因球阀关闭引起的直接水锤,使用流体力学计算软件进行了管道水锤三维建模和模拟。方成跃等研究了波速变化对管道内水锤压力波幅值与周期的影响。易平研究了各种工况下的关阀时间与水击压力的关系。
本文采用Flowmaster软件对船舶压力注水管道系统进行建模,对水锤的产生过程进行模拟,讨论关阀时间对水锤的影响,并提出压力注水管道水锤的两种防护措施。
1 管道水锤的基本理论
水锤波速作为管道内压力波的重要参数,对压力波的影响主要体现在压力波幅值与传播周期两个方面。弹性水锤波速理论公式的计算公式如下:

式中,a为水锤波速;K为流体的体积弹性模量;ρ为流体密度;D为管径;E为管壁材料的弹性模量;e为管壁厚度;c1为管道支撑相关系数。
根据Joukowsky水锤的经典计算公式,可以得到管道内部的压力变化:

式中,ΔP为管内压力变化;ΔV为管内流体速度变化;ρ为管内流体的密度;a为水锤的波速。
据牛顿第二定律和质量守恒定律,可得到的水锤基本方程:
运动方程:

连续方程:

式中,V为管线中流体速度;x为距离;t时间;H为测压管的水力坡度线高度;D为管线直径;α为管线轴线与水平面的夹角;f为摩阻系数;g为重力加速度;a为波速。
2 管道水锤现象仿真分析
Flowmaster是一维工程流体管道系统分析软件,其具有丰富的元件库,可方便快捷地搭建系统仿真模型,擅长对流体管路系统进行整体分析。该软件基于特征线法,把流体管道作为研究对象,对整个系统进行分析。Flowmaster在进行仿真计算时,将系统模型看作由一系列流体元件组成,元件之间通过节点相互连接,各个元件通过连续性方程和动量方程来描述。因此,整个系统的仿真被简化成为求解线性方程组的问题。
以某船舶压力注水系统为例,系统原理图如图1所示,该系统将压力海水注入至水舱内,由于在水舱注水完成后,球阀需要快速关闭,因而产生水锤现象。

图1 某船舶压力注水系统示意图
使用Flowmster对该系统进行建模,模型如图2所示。系统中弯管、接头等均用离散损失元件Discrete Loss代替。海水压力为30bar;管道3、管道4长度均为50m,管道直径为0.1m,波速为1000m/s;阀门直径为0.1m;水舱为敞口水舱,表面压力为1bar。

图2 压力注水系统模型
阀门控制信号如图3中灰线所示,阀门在0~2s时开度为1,0.5内关闭(2.5s时完全关闭)。图3是节点3处的水锤压力随时间变化曲线,正常工作时,节点3处的压力为15.53bar;阀门关闭后,节点3处的压力峰值达到81.77bar,为正常状态下的5.3倍,并且压力出现周期性波动。由于阀门的突然关闭导致压力注水管道出现了明显的水锤现象,而且压力峰值远高于正常工作状态。

图3 水锤压力随时间变化曲线
3 管道水锤防护措施
在压力注水管道系统中,影响水锤产生的因素有管路参数(管长、横截面积)、管道连接方式、部件参数(如阀门参数)、操作方式(如阀门关闭方式)等。因此,根据当前系统的特点,本文采取以下防护措施:改变关阀方案、安装抑制水锤装置等措施。
3.1 关阀方案对水锤现象的影响
水锤是由于阀门的突然启闭,使管道内的流速发生突然变化,从而引起对管道的压力冲击。因此可以通过适当延长关阀时间,改变关阀方式降低水锤峰值压力。根据上述的措施,制定如表1所示的不同的关阀方案,并对4种关阀方案进行研究。阀门开度与时间关系如图4所示,不同关阀方案下水锤压力如图5所示。
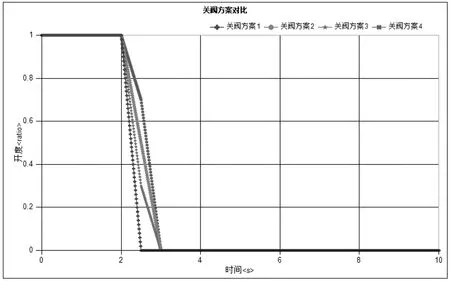
图4 不同关阀方案对比

表1 关阀方案对比
从图5中可以看到,四种关阀方案的水锤峰值压力分别为81.77bar、38.07bar、24.36bar、53.49bar。对比关阀方案1和关阀方案2可以看到,同样是线性关闭阀门,阀门关闭时间延长,管道内的水锤压力将会减小;对比关阀方案2与关阀方案3可以看到,当总的关阀时间不变,采用两阶段双速关闭阀门时(第一阶段快关,第二阶段慢关,即凹曲线),管道内的水锤压力有明显降低。对比方案2与方案4,当总的关阀时间不变,采用两阶段双速关闭阀门时(第一阶段慢关,第二阶段快关,即凸曲线),管道内的水锤压力却上升。

图5 不同关阀方案的水锤压力
因此,在球阀阀门关闭时间可调的情况下,适当地延长球阀的关闭时间是一种有效降低管道水锤压力的方法。采用两阶段双速关阀的方案时,在相同的关阀总时间下,凹曲线能够进一步降低管道水锤压力。
为了研究两阶段双速关阀方案中,凹曲线斜率对水锤压力的影响,制定如表2所示的不同的关阀方案,阀门开度与时间关系如图6所示,不同凹曲线关阀方案下水锤压力如图7所示。
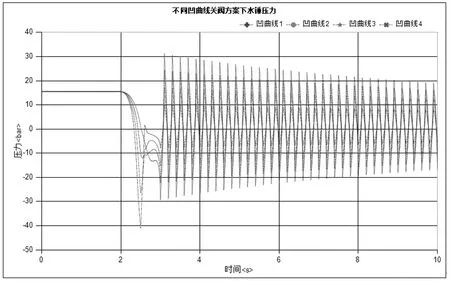
图7 不同凹曲线关阀方案下水锤压力
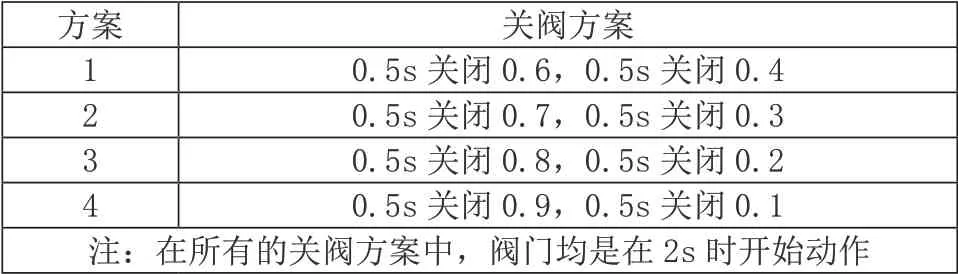
表2 关阀方案对比

图6 不同凹曲线关阀方案对比
从图7中可以看到,阀门完全关闭时水锤压力峰值分别为31.18bar、24.36bar、17.30bar、8.96bar,随着凹曲线第一阶段关阀速度的增加,对水锤波动的峰值压力越来越小。但是,随着凹曲线第一阶段关阀速度的增加,在关阀第一阶段结束时出现了新的压力峰值-13.19bar、-11.96bar、-26.48bar、-41.04bar,并且随着第一阶段关阀速度的增加,该峰值逐渐增大,凹曲线4的第一阶段结束时的压力峰值甚至超过了关阀结束时的水锤压力峰值。因此,两阶段双速关阀曲线第一阶段的关阀速度不是越大越好,还应注意第一阶段结束时的压力值变化,使其不超过关阀结束时的水锤压力峰值。
通过多次仿真对比,提出一种双速关阀曲线该曲线如图8所示,第一阶段关闭阀门的3/4,第二阶段关闭阀门的1/4,此时,对水锤的抑制效果最好,并且由于第一阶段关阀产生的压力峰值未超过关阀结束时的水锤压力峰值。

图8 一种关阀曲线及水锤压力
图9 为所提出的关阀方案的末端管道受力图。从图中可以看到,管路受到5Hz、15Hz的冲击力,若系统某处的固有频率为5Hz、15Hz,将有可能导致共振,对系统造成危害。因此,改变不同的关阀方式能够有效降低管道水锤压力的峰值,但是,周期性波动现象仍然存在,依旧会造成管道系统的周期性振动。
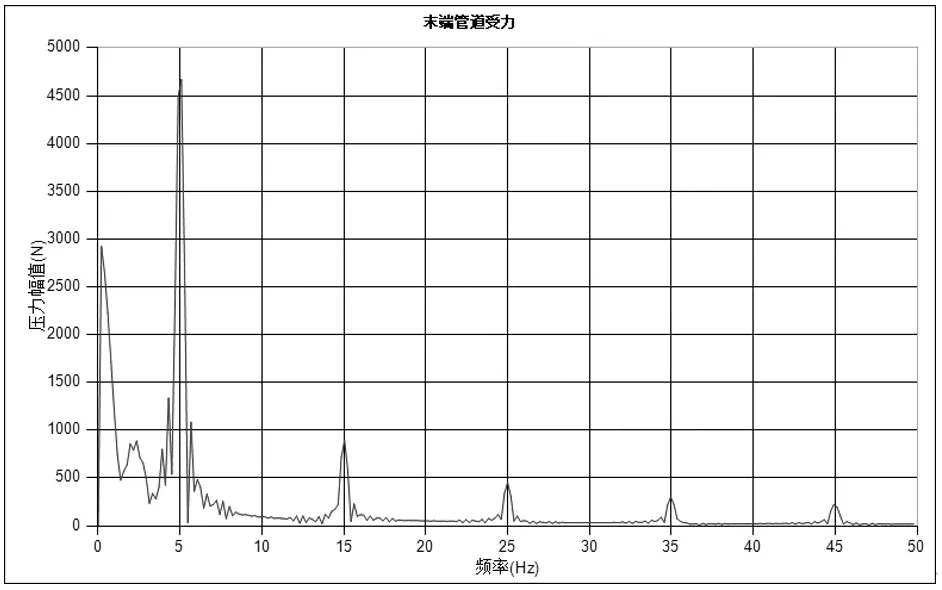
图9 末端管道受力图
3.2 安装抑制装置对水锤现象的影响
在管道中增加水锤抑制装置能对水锤的幅值及波动进行有效的抑制,考虑到船舶系统的安装空间及使用条件,为保护系统末端设备,采取了以下水锤防护措施:在球阀后安装放气阀;在球阀后安装稳压罐。模型如图10所示。

图10 安装两种水锤抑制装置模型
从图11中可以看到,安装两种抑制装置后,管道水锤压力峰值得到明显抑制,而且压力波变化非常平稳。放气阀对管道水锤波动效果的抑制优于稳压罐,安装稳压罐的管道系统在阀门关闭后,由于海水流速的突然变化,出现短时的负压,而且在恢复稳定的过程中有幅值较小的波动。

图11 安装抑制装置后管道水锤压力
4 结语
本文使用Flowmaster软件对某船舶压力注水管道系统进行建模,对管道的水锤现象进行了数值模拟,研究了关阀方式以及安装水锤抑制装置对水锤现象的影响。得到结论如下:
(1)压力注水管道中,延长阀门关闭时间,管道内水锤压力将会减小。相同的关阀总时间,采用凹曲线两阶段双速关闭的方案,能够进一步减小管道内水锤压力。
(2)凹曲线第一阶段的关阀速度不是越大越好,还应注意第一阶段结束时的压力值变化,使其不超过关阀结束时的水锤压力峰值。
(3)改变不同的关阀方式能够有效降低管道水锤压力的峰值,但是水锤压力仍然进行周期性波动,依旧会造成管道系统的周期性振动。
(4)在注水管道中安装稳压罐及放气阀不仅能够有效抑制管道内水锤压力峰值,而且能够抑制水锤压力的周期性波动,放气阀对水锤压力波动的抑制效果优于稳压罐。

