台风暴雨型滑坡地下水位动态特征及预测

伍剑波,王赫生,张泰丽,孙 强,朱延辉

(中国地质调查局南京地质调查中心,江苏 南京 210016)

作为塑造地貌最活跃的外营力之一,地下水主要通过物理、化学、力学等形式参与地质体的水-岩(土)相互作用,促进地质体向不良方向演变,并在某种程度上诱发了地质体灾变的发生[1-5]。台风暴雨常引起强烈的地下水位波动及斜坡地质体结构变化,从而使地质体发生滑移、拉张变形等,这类滑坡称为台风暴雨型滑坡。台风暴雨型滑坡多见于我国东南沿海地区,台风暴雨与一般降雨诱发滑坡的成因机理相似,但又与一般降雨形成的滑坡存在显著差异[6]。台风暴雨型滑坡具有规模小、厚度浅、突发性(或突变性)强等特征,属于典型的降雨诱发型滑坡,其灾变过程与滑坡体地下水位波动密切相关[7-11]。由于台风期暴雨持续时间长、强度大、降雨量集中,所以滑坡在其作用下具有地下水反应灵敏、渗流速度快、波动幅度大等特点[12]。因此,掌握地下水位动态规律,高效和准确地预测水位趋势,对于台风暴雨型滑坡的防治、预警预报、稳定性评价等具有重要的理论价值与实际意义。

目前,地下水位动态变化分析预测的方法主要有物理模型法、数值模拟法和数理统计模型法等[13-21]。物理模型法是反映含水系统和理解其物理过程的主要手段[21],如坡地水文模型,主要基于大量观测资料和相关水文地质参数得出较精确的预测结果,建模需简化相关条件。数值模拟法能准确模拟不同降雨模式和复杂地层结构条件下地下水的变化,如有限差分法、边界元法,但数值模拟预测滑坡区域地下水位变化时,无法模拟隐藏裂隙产生的优先流,且存在降雨入渗补给滞后性的处理问题[22]。数理统计模型法是基于已有的自变量和因变量数据确定两者之间的关系函数,进而进行因变量的预测,如回归分析模型、灰色动态模型、时间序列分析模型等已广泛应用于地下水位预测。但是回归分析模型多以线性理论为基础,考虑问题简单化,灰色动态模型很难反映地下水周期性波动的特点[20],时间序列分析模型当含水系统水动力条件发生变化时,已建立的模型将不再适用,无法适应非稳定变量的观测序列[23]。

径向基函数神经网络(Radical Basis Function Neural Network,简称RBFNN或RBF神经网络)能逼近任意的非线性函数,可以处理系统内难以解析的规律性,具有良好的泛化能力、较快的学习收敛速度及较强的非线性映射功能[24],通过对数据样本进行深度学习,可无限逼近真实值。RBF神经网络的主要优势是能够模拟非线性系统,可定量表示变量间复杂的函数关系,可以在没有任何假设的条件下模拟水文地质变量间复杂的非线性关系[24]。因此,该模型更适用于滑坡地下水位在时间序列上动态波动的预测[23,25-28]。目前,地下水位预测模型多用于地下水位变幅或大时间尺度(年、月)水位值的预测,而对日水位值的预测较少。本文基于长期监测的水文地质数据,分析降雨对地下水位变化的影响,通过构建RBF神经网络模型对地下水位动态进行预测,探讨各种降雨条件下地下水位动态特征及预测效果。

1 RBF神经网络模型

1.1 RBF神经网络简介

径向基函数(RBF)是某种沿径向对称的标量函数,通常定义为空间中任一点x到某一中心c之间欧氏距离的单调函数,记作k(‖x-c‖),其作用往往是局部的,即当x远离c时函数取值很小。常用的RBF函数[29]如下。

f(x)=exp-(x/σ)2,

(1)

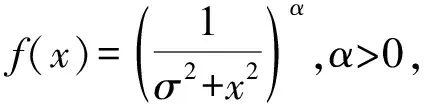
(2)

f(x)=(α2+x2)β，α<β<1。

(3)

RBF神经网络是基于径向基函数建立的一种人工神经网络[30],属于前向神经网络类型,能够以任意精度逼近任意连续函数。

1.2 RBF神经网络结构及运算

RBF神经网络由3层结构组成(图1)。第一层为输入层(X),由信号源结点组成;第二层为隐含层(H),隐单元数根据描述问题的需要而定,隐单元的变换函数是径向基函数,是对中心点径向对称且衰减的非负非线性函数;第三层为输出层(Y),对输入模式的作用给出响应。从输入层节点只传递输入信号到隐含层,隐含层节点由像高斯函数(公式(4))辐射状作用函数构成,是非线性的,从隐含层节点到输出层节点变换是简单的线性函数。

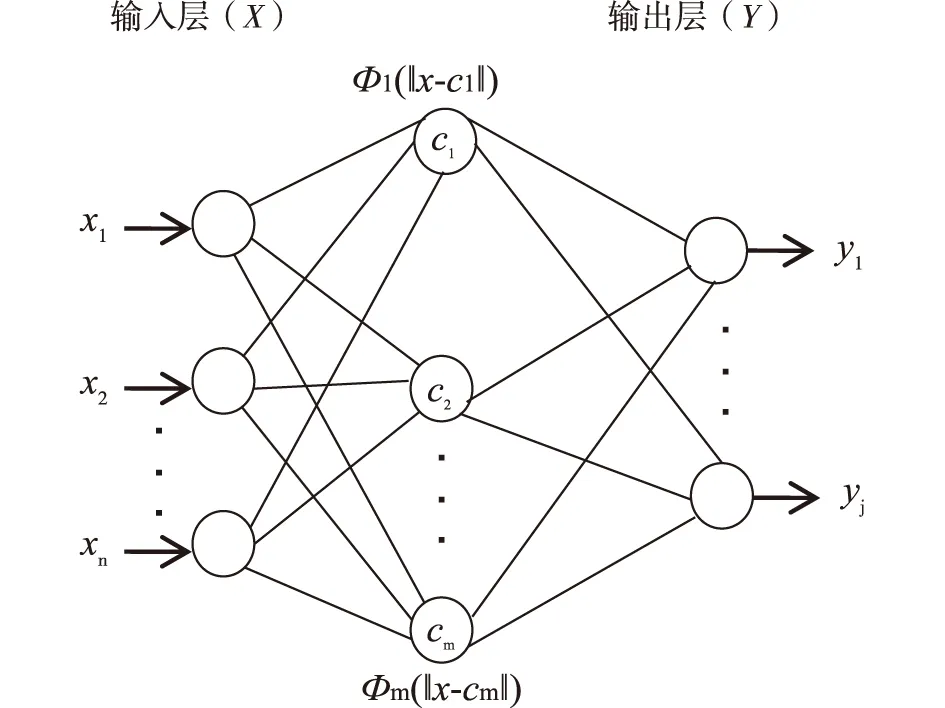
图1 RBF神经网络结构Fig. 1 Structure of RBFNN

本文建立的RBF神经网络采用高斯分布函数[29]

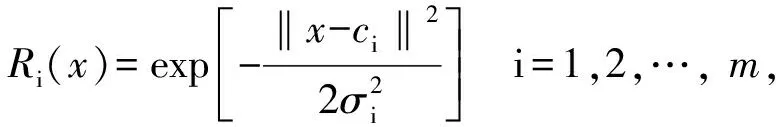
(4)

式中:x为n维输入向量;ci为第i个基函数的中心,与x具有相同维数的向量;σi为第i个感知的变量,决定基函数围绕中心点的宽度;m为感知单元的个数(隐含层节点数)。‖x-ci‖为向量x-ci的范数,通常表示x与ci之间的距离;Ri(x)为径向对称的非线性函数值,其值越大代表预测值越接近真实值。

Ri(x)在ci处有1个唯一的最大值,随着‖x-ci‖增大,Ri(x)迅速衰减至0,对于给定的输入x∈Rn,只有小部分靠近x的中心被激活。

RBF神经网络学习分为两步:第一步通过聚类算法得到初始权值;第二步根据训练数据训练网络权值。

2 台风暴雨型滑坡地下水位动态

2.1 台风暴雨型滑坡渗流与变形特征

台风暴雨诱发的滑坡可以分为突变型滑坡和缓动型滑坡,缓动型滑坡相对于突变型滑坡发生率更低、规模更大,危害范围更广[6]。

中林滑坡位于浙江省文成县56省道中林大桥北侧,常年受台风暴雨影响。受台风“泰利”影响,该滑坡于2012年6月19日下午6时发生变形破坏,滑坡中上部出现多处裂缝,裂隙长10～30 m,宽2～30 cm。前缘公路边坡及坡脚处发生连续滑塌,规模约300 m3。滑坡位于斜坡中下部,呈长舌状,滑坡前缘高程198～203 m,后缘高程238～241 m,滑坡高差约58 m,水平投影长约107 m,宽约47 m,滑体厚2.5～8.0 m,规模约14 000 m3。滑坡呈上陡下缓之势,坡度为31°～24°,呈梯田台坎状,台坎高1～2 m(图2)。滑坡发育于白垩纪朝川组中,滑体物质主要为呈散裂结构和碎裂结构的强-全风化凝灰岩,滑床为中等风化凝灰岩(图3)。

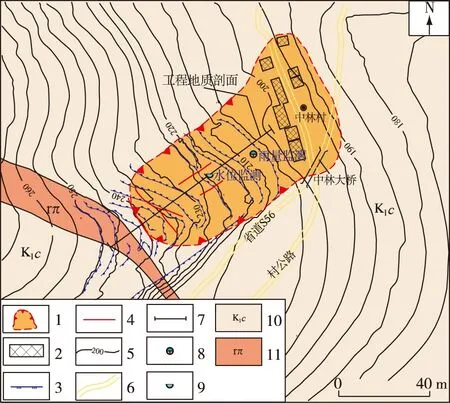
1.滑坡范围;2.威胁房屋;3.陡坎;4.裂缝;5.等高线;6.公路;7.工程地质剖面;8.雨量计位置;9.水位计位置;10.早白垩世朝川组;11.钾长花岗岩脉图2 中林滑坡平面示意图Fig. 2 Plane diagram of the Zhonglin landslide

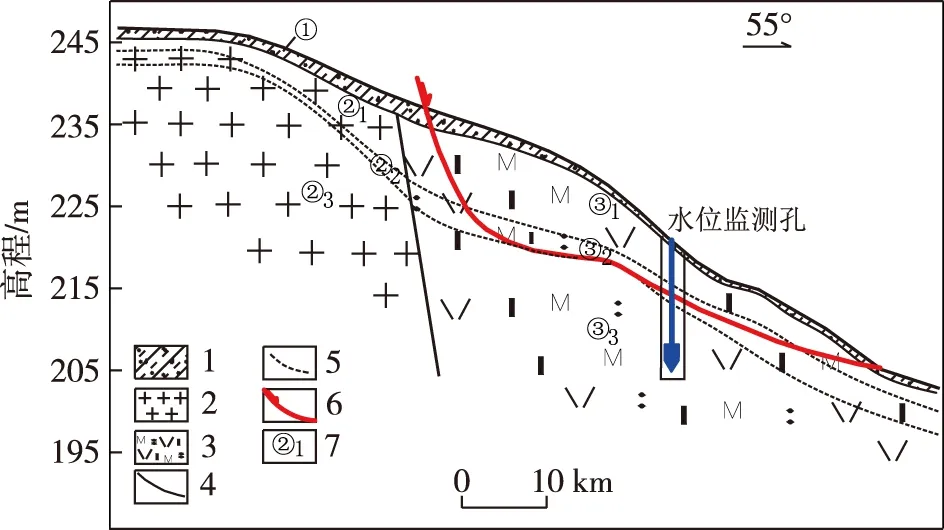
1.含角砾粉质黏土;2.花岗岩;3.流纹质熔结凝灰岩;4.地层界线;5.风化层界线;6.潜在滑动面;7.工程地质层分层编号(①为残坡积层；②1、③1为全风化层；②2、③2为强风化层；②3、③3为中风化层)图3 中林滑坡工程地质剖面Fig. 3 Engineering geological section of the Zhonglin landslide

对该滑坡模拟了台风暴雨的等强度降雨、渐变强度降雨两种常见工况下滑坡地下水的暂态渗流场及稳定性[6],结果显示两种工况下滑坡地下水渗流特征基本相同。随着降雨的进行,4.8 h后地下水位上升明显,滞后时间短,24 h内地下水位达到强风化和中风化接触面附近,且在坡脚形成溢流,而天然降雨状态下,地下水位位于滑动面以下。随着地下水位上升,稳定系数快速下降;水位稳定以后,稳定系数下降速度减慢。

通过对位移、地下水位、雨量等历史监测数据进行分析(图4,图5),发现滑坡中部位移有突变现象,与降雨、地下水存在明显的关联性。“莫兰蒂”台风期间,9月14日该区降雨量为225 mm,地下水位上升至8.86 m,为历史高水位(达到滑面附近);9月15日滑坡累计位移发生第一次突变。“鲇鱼”台风期间,9月28日该区降雨量为368.5 mm,地下水位上升至7.1 m,为历史最高水位(超过滑动面位置);9月29日滑坡累计位移发生第二次突变,位移变幅达到历史最高值(图5);位移突变比地下水位突变滞后1天,地下水位达到滑动面附近才引发位移突变。因此,监测数据进一步佐证了文献[6]模拟结果,台风暴雨期地下水位达到滑动面附近,基质吸力降低、孔隙水压力增加是滑坡产生变形破坏的主要原因。

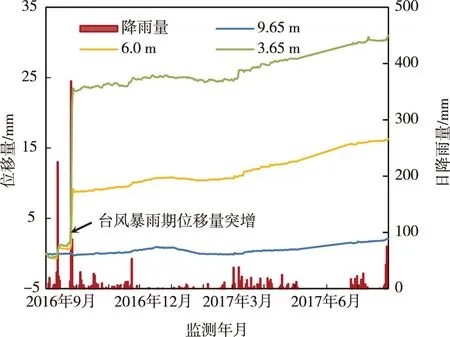
图4 日降雨量与滑坡中部不同深度位移变化图Fig. 4 Relation between daily rainfall and displacement variation of different depths in the middle of the landslide

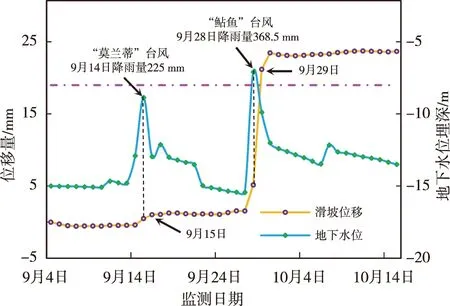
图5 地下水位与滑坡位移变化图Fig. 5 Relation between groundwater level and landslide displacement

综上所述,推断中林滑坡为拉裂-蠕滑变形破坏模式,降雨是其主要诱发因素,属于典型的缓动型台风暴雨滑坡。

2.2 数据采集与预处理

滑坡的岩土体物质组成不会随降雨量的变化而变化,仅物理力学参数发生改变,属于固定的参数值,对地下水位动态预测无实用意义,因此本文预测时不作考虑。降雨与地下水位之间的关系密切,相互影响处于动态变化,所以,这两种水文参数可以作为模型的训练学习样本。

中林滑坡中部位移变形最明显(图4),滑坡地下水位计(带气压校正计,型号为DI601,量程为20 m,精度为2 mm)安装于滑体中部(图2,图3)。由于滑坡面积尺度小,四周开阔无遮挡物,滑坡区不存在小气候现象,降雨量多均匀分布,考虑设备安装条件,雨量计(型号为SRY-1,量程为5 mm/min,精度为0.1 mm)置于滑体中下部(图2)。地下水位计和雨量计分别用于监测地下水位和降雨量,其中水位采集频率为4 h/次,降雨量每测0.5 mm精度自动记1次。

本次分析的数据以天为时间尺度,当日24时的观测水位值与前一日24时至当日24时的累计降雨量值相对应。降雨量和水位观测从2016年1月1日—2018年6月28日,监测时长910天,数据样本共910组。

2.3 降雨与地下水位响应关系

中林滑坡位于台风主要影响区,通过统计2016—2017年的降雨数据(图6),发现其年平均降雨量为2 168.5 mm,年度无雨期<198天,中雨以上的降雨期>50天。2016年各级别的降雨天数均大于2017年各级别的降雨天数。2016年9月15日和9月28日,分别受台风14号“莫兰蒂”和17号“鲇鱼”影响,该区普降大暴雨、特大暴雨,日降雨量百年一遇,地下水位响应迅速,当日出现年度最大涨幅(图7)。

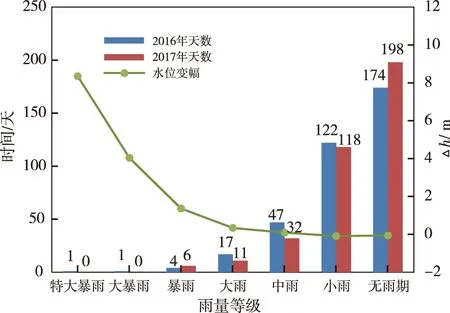
图6 不同级别降雨天数与地下水位变幅统计图Fig. 6 Variation statistics of groundwater level on different rainy days

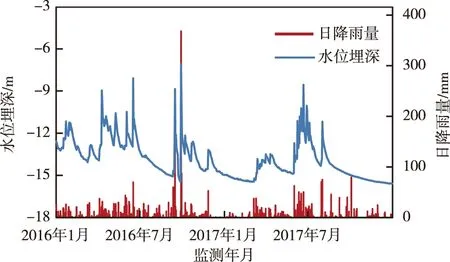
图7 日降雨量与地下水位变化关系图Fig. 7 Relation between daily rainfall and groundwater level

由图6可知,地下水位变幅与降雨级别呈正相关,降雨量越大,地下水位涨幅越大。由于小雨下渗的水量少,其形成的湿润锋面难到达地下水位界面,因此对水位影响微弱。

随时间的波动,降雨量与地下水位表现出较好的一致性。暴雨条件下地下水位变化最大,其次是连续性降雨,地下水位与降雨量之间呈明显的正相关(图7)。

为了分析降雨对地下水位的滞后影响,对降雨量和地下水位数据作进一步处理。借鉴文献[19]的处理方法,地下水位变幅Δh(t)与地下水位h(t)关系式为

Δh(t)=h(t)-h(t-1)。

(5)

根据公式(5)求出每天水位变幅,Δh(t)与h(t)之间存在一定的相关性(图7),下界包络线表示在无雨情况下的观测孔水位下降曲线f(h) (图8)。通过Δh(t)减去对应的f(h),排除自然排水过程对水位变化造成的影响,最后得到受降雨影响的地下水位变化值ΔY(t)。

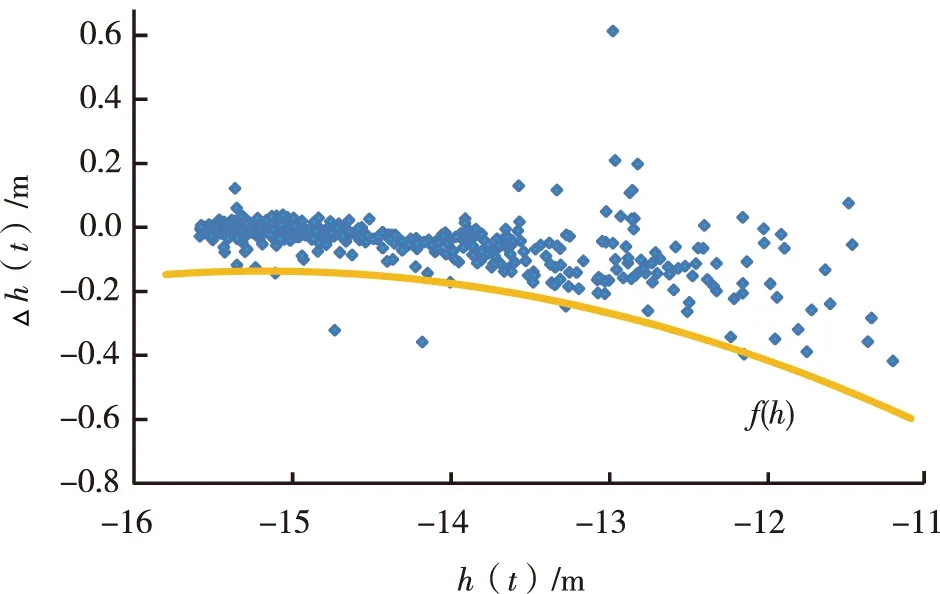
图8 地下水位与地下水位变幅关系图Fig. 8 Diagram of groundwater level and groundwater level variation

ΔY(t)与前30天(降雨当天为第1天)影响期为τ时的降雨量X(t-τ)作偏相关分析,二者积差相关性系数r如图9所示。相关性系数r呈波动性减小,第1天相关系数最大,显著性明显;第2天以后相关系数大幅减小,3～6天相关系数均<0.1,显著性不明显;第10天相关系数增大,主要为降雨周期的叠加效益。因此,降雨对中林滑坡当天的地下水位影响最显著,第二天降雨对地下水位影响减小,滞后周期为1天。出现此现象的原因是,该滑坡属于浅层滑坡,强、全风化凝灰岩与浅表坡积层组成的滑体透水性好,雨水下渗速度快,地下水位响应迅速。此外,滑坡位于斜坡中下部,呈台坎形,坡度陡,前缘为屋后切坡,正地形,这些因素导致地下水补给排系统反应快速。

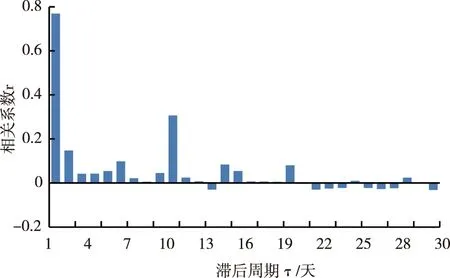
图9 地下水位变幅与降雨量关系图Fig. 9 Relation between groundwater level variation and rainfall

3 滑坡地下水位预测

3.1 RBF神经网络模型的建立

本文采用降雨量、地下水位2个因子进行地下水位动态预测。RBF神经网络模型进行训练学习时,降雨量作为输入变量,地下水位作为输出目标变量。考虑实测数据的完整性,选用2016年1月1日—2018年2月28日的790组数据作为训练样本,2018年3月1日—2018年6月28日的120组后期数据用于测试样本。

基于Matlab工具箱中newrb函数创建RBF神经网络。函数格式为net=newrb(P,T,GOAL,SPREAD,MN,DF)函数中P为由降雨量组成的输入向量集;T为由地下水位组成的目标向量集;GOAL为均方误差,设为10-8;SPREAD为径向基函数分布密度,参数通过样本数据训练,不断修正初始值获得最佳值,本文取值为100.82。MN为神经元最大数量,一般取输入样本数量,本文取值为790。DF为两次显示之间添加的神经元神经数目,设为1。

3.2 地下水位动态预测

基于RBF神经网络模型预测的地下水位动态预测值与实测值对比结果如图10所示。相同降雨条件下,预测曲线与实测值曲线形态较一致,峰值发展趋势较贴近。对比测试样本中的地下水位与降雨量,发现实测的部分强降雨不一定引起地下水位大幅度波动,如监测时间45天和68天(图10),降雨之前均有>5天的无雨期或少雨期,加之土地利用类型为耕地,正属于春季耕种期,植被干枯少水,坡体内非饱和区范围大,土壤含水率低,下渗的水体多被土壤包气带吸收,降雨形成的湿润锋面难到达地下水位界面,导致强降雨引起的地下水位变幅<0.1 m,而预测水位波动明显,预测值与实测值不一致。

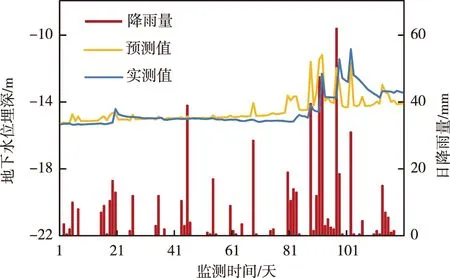
图10 RBF神经网络模型预测值与实测值关系图Fig. 10 Relation diagram of RBF neural network model predicted value and measured value

3.3 预测精度分析

3.3.1 精度

(1)以年、月为时间尺度,大部分预测精度较高,但不能较好地表达地下水动态变化特征。

(2)以日、小时为时间尺度,以水位变幅值、水位值为预测对象,变幅值预测结果偏差多<0.5 m,水位值预测结果偏差多为2～5 m。基于水位变幅值进行预测,结果存在的问题是变幅值转换为水位值时,变幅偏差值(实测值与预测值之间差值的绝对值)的累计值可能导致预测值与真实值偏离较大。

本文以日地下水位值为预测对象,通过对比分析预测值与真实值,得出RBF神经网络模型预测的偏差最小值为0.01 m,最大值为3.13 m,平均值为0.46 m。与上述其他预测模型预测精度相比,RBF神经网络模型的预测精度能达到水位变幅的预测精度,高于其他水位值的预测精度,能较好地反映地下水位动态。

3.3.2 精度影响因素

在不同降雨工况条件下,地下水位预测难易程度不同,预测精度也有一定差别。在连续性强降雨条件下(图10),预测曲线与实测曲线贴合最差,如监测时间16～20天、80～83天、88～102天;不同降雨量或不同降雨类型预测值的平均偏差不同,降雨量越大,平均偏差越大,暴雨平均偏差为1.786 m、大雨平均偏差为1.481 m、中雨平均偏差为0.747 m、小雨平均偏差为0.369 m、无雨期平均偏差为0.328 m(表1)。同类降雨级别样本越少,预测精度越低;无雨期样本数量最多,预测精度最高;暴雨期样本数量最少,预测精度最低。

表1 不同类型降雨预测精度与样本数量关系

出现上述现象的原因为:①与参与模型训练的样本分布有关,有限的数据样本制约了模型反应变量之间相互作用的关系;②地下水循环系统复杂多变,RBF神经网络模型仅考虑了降雨量,未考虑其他地质参数;③监测设备误差可能导致原始数据偏离真实数据,间接影响模型预测精度。

4 结论

(1)排除自然泄水影响因素,地下水位对降雨的响应滞后期<1天,即地下水位变化主要与当天降雨量有关。地下水位变幅与降雨级别呈正相关,尤其台风作用下极端降雨引起地下水位迅速上升至滑面,是滑坡位移突变的主要因素,也是台风暴雨型滑坡的主要特点之一。

(2)RBF神经网络模型预测结果显示:预测值曲线与实测值曲线形态较一致,峰值发展趋势也较相近,可较好地体现地下水位非线性动态变化特征,预测值的平均偏差为0.46 m,能准确模拟小时间尺度、长时间序列地下水位涨落过程。

(3)与其他地下水位预测方法相比,基于MATLAB软件建立的RBF神经网络模型方法简单、学习速度快、使用便捷,可以通过有限的观测资料获得理想的预测结果,实用性较好。