大型地下组合结构抗震计算方法的分析与选择
王航 杜玉东
北京市市政工程设计研究总院有限公司 100082
引言
我国是一个多震国家,尤其是2008 年以来接连发生汶川地震、北川地震、青海玉树地震、云南盈江地震、四川雅安地震、甘肃地震等不同等级的地震,使地震的话题受到广泛关注。随着社会经济的发展,土地资源的短缺,城市交通的压力越来越大,为拓展城市空间,地下空间的发展日益受到重视。近年来地下结构已经在轨道交通、物流、管廊、铁路、公路交通运输中得到了广泛的应用,同时人们也逐渐意识到地下空间的有限性,集约式、综合功能式地下结构成为目前地下结构发展的趋势。这种复杂的地下结构在地震时的安全问题,对于人民生命财产的保障以及城市生活的正常运行,具有极为重要的意义。
1 地下结构的地震反应特点
在地震作用下,地下结构与地面结构的振动特性有很大的不同,主要表现为[1]:
(1)地下结构的振动变形受周围土体的约束作用显著,结构的动力响应一般不明显表现出自振特性的影响。而地面结构的动力响应则明显表现出自振特性,特别是低价模态的影响。
(2)一般而言,地下结构在振动中的主要应变与地震加速度大小的联系不很明显,但与周围岩土介质在地震作用下的应变或变形的关系密切。对地面结构来说,地震加速度则是影响结构动力反应大小的一个重要因素。
(3)地下结构的地震反应随深度发生的变化不很明显。对地面结构来说,埋深是影响地震反应大小的一个重要因素。
(4)对地下结构和地面结构来说,其与地基的相互作用都对其动力反应产生重大影响,但影响的方式和影响的程度则是不相同的。
总的来说,结构的自振特性与地基振动场对结构的动力反应均会产生不同程度的影响:对地面结构来说,结构的形状、质量、刚度等自振特性,对结构的地震反应具有决定性作用;而地基的运动特性对地下结构的地震反应起主要作用,相比较结构的形状和自振特性,对结构反应的影响相对较小。因此,在当前所进行的研究工作中,对地面结构来说,结构自振特性的研究占很大的比重,而对地下结构来说,地基地震动的研究则占比较大的比重。
2 地下结构抗震计算方法的选择
结构抗震计算的方法,目前比较成熟的计算方法可以分为三类,即地震系数法(又称拟静力法、惯性力法)、地层位移法(反应位移法)和时程分析法。地震系数法发展最早,基本在20 世纪六七十年代以前,地下结构抗震计算基本采用的都是地震系数法,70 年代以后,随着地下结构的发展和人们对地下结构认识的深入,地下结构的抗震设计才逐渐形成本身独立的体系。对于一些大型、复杂的地下结构,其地震作用下的动力响应,既无法通过实验去判断,也很难找到类似的事故案例,只能借助于结构的模拟计算。随着有限元分析手段的进步,计算本身的复杂性不再是制约问题解决的关键,而结构体与周围边界的模拟,或者说地震对结构的作用方式成为问题的关键。
2.1 地震系数法(惯性力法)
当结构物的质量密度较大,超过周围土层的质量密度,或者基坑开挖时设置了支护桩,导致结构周围的填土不密实,地震引起的土层作用不能有效作用于结构,结构在地震响应主要表现为自振特性,惯性力起决定作用,此时应该采用地震系数法。地上建筑物的抗震计算多是基于这样的理论。其计算图示见图1。
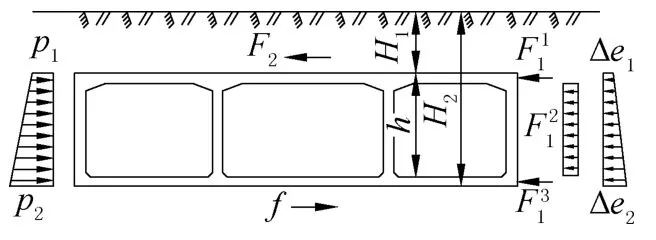
图1 地震系数法动力计算图示Fig.1 Dynamic calculation diagram of seismic coefficient method
地震系数法的计算荷载主要包括:结构惯性力(顶底板和侧墙,Fi1(i=1,2,3));结构上方土柱的惯性力(F2);土层的被动土压力(p1~p2);主动侧向土压力增量(Δe1~Δe2);底板与地基之间的基底摩擦力(f,只有当需要地层提供的水平抵抗力(即所有惯性力的总和)大于地层能够提供的被动土压力时,结构底板与地基之间存在摩擦力)。
《建筑抗震设计规范》[2]中关于地下建筑的抗震计算模型的条文中说明:与周围挡土结构分离的内部结构,可采用与地上建筑同样的计算模型,即地震加速度法,也就是惯性力法。但是采用地震系数法计算地下结构存在一定的问题:
首先是上层填土,建筑结构的地下结构,或者作为地面建筑结构的基础,或者是裙房,上面无填土或填土不厚,地震动情况下,结构是可以驮着上面的土体来运动的,上部填土的惯性力施加到结构上偏于保守,但是可以接受。这种方法用到市政结构上的时候,因为上部填土很厚,5m、6m甚至超过10m,这时候用惯性力法来计算,上部填土的惯性力非常大,都施加到结构上计算过于保守。
其次,地震加速度的取值,是与所采用的抗震计算方法有关系的,地震系数法中计算惯性力时采用的场地设计地震动加速度反应谱,需要考虑动力放大系数βm,《城市轨道交通结构抗震设计规范》[3]中给出βm最大值为2.5。而反应位移法中计算惯性力时采用的场地设计地震动加速度反应谱没有计入动力放大系数,是与地震动位移相一致的地震动加速度。所以忽略周围土体作用,采用地震系数法计算地下结构过于保守。
2.2 时程分析法
时程分析法又称直接动力法,采用时程分析的主要目的,一是获得结构在地震动整个过程中每个时刻的地震反应,二是可以计算结构在非弹性阶段的地震反应,暴露结构的薄弱环节。但是这要基于正确的地震波选择或人工模拟。
很多文献认为时程分析是最能真实反应结构的动力特性的,随着计算机能力的增强和计算手段的研发,时程计算也不是什么困难的事情。但是时程分析中采用的地震波,其特性、波长、输入方向等等很多因素都是人为确定的,即使是测量到的真实地震波,由于场地条件、施加方向等因素,也无法推断计算对象真实的动力反应。另外,时程分析多是以地震加速度的形式施加于结构上,对于地上结构更为适合,对于地下结构,结构与边界之间如何模拟的问题依然存在。因此,尽量准确地模拟结构的边界条件,了解地下结构的动力响应特点,分析地震如何通过土层对结构产生作用的机理,并借助于一定的经验公式,对结构做出定量的判断,比运用时程进行定量分析更具有确定的包络作用。
2.3 反应位移法(地层位移法)
当结构的质量密度小于或等于围岩的质量密度时,结构的变形主要取决于周围地层的变形,惯性力的影响相对较小时,宜采用反应位移法,隧道结构多采用反应位移法[4]。
反应位移法中,土体对结构的作用,主要用土层的相对位移和结构周边土层剪力(结构顶面剪力τu、底面剪力τB、侧面剪力τs)来体现,与地震系数法最大的不同是,结构自身的惯性力在地震响应中占有较小的比例。
反应位移法的关键是地下结构的模型,应能够准确地反应土层与结构的关系,即地层的地震动能够真实地传递到结构上去,通常结构四周用土弹簧支撑,如图2 所示,kv为结构顶底板径向地基弹簧刚度;ksv为结构顶底板剪切地基弹簧刚度;kh为结构侧壁压缩地基弹簧刚度;ksh为结构侧壁剪切地基弹簧刚度。这就要求传递位移的土弹簧能够真实反映结构周围土体的特性。计算中土弹簧的支承刚度和剪切刚度通常由地勘部门提供的基床系数决定。
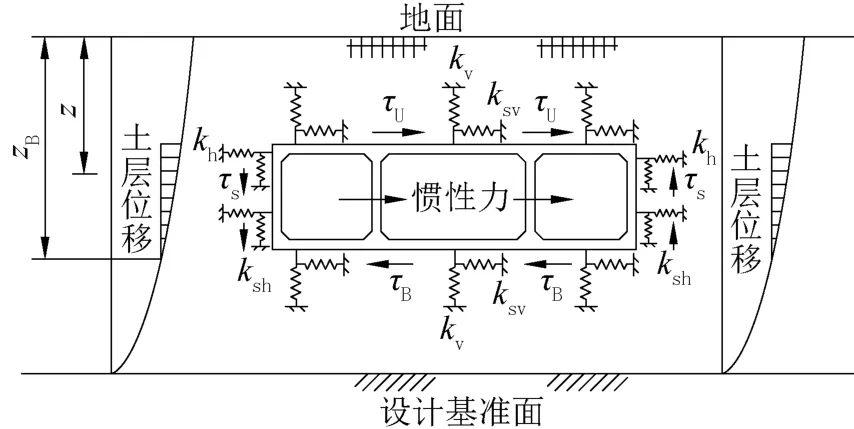
图2 反应位移法动力计算图示Fig.2 Dynamic calculation diagram of reactive displacement method
反应位移法(地层位移法)也存在一定的问题:
第一,采用弹簧模拟土的作用以及土和结构的关系,本身就有一定的缺陷,计算结果有较大的误差。计算中发现,土弹簧的变化对于结构内力的计算有很大的影响,但是土弹簧刚性值有很大的不确定性,目前获得弹簧刚度的手段无外乎载荷试验、地震观测、有限元模型计算,但是这些方法都具有一定的局限性;
第二,模型本身带来的误差。目前多用的方法是基于温克尔假定,土弹簧之间是独立不相关的,使得地震时土体自身之间的相互作用体现不出来,也不能真实反映与土体连接的结构角部的应力畸变现象;
第三,对于明挖结构,基坑开挖的方式不同,决定了结构形成以后周围填土的密度情况区别很大。如果后填土的质量密度小于钢筋混凝土结构,在结构周围很难形成坚硬的外壳,从而违背了反应位移法成立的基本假定,那么采用反应位移法计算的准确性就是一件值得商榷的问题。
地下结构是否采用反应位移法进行抗震计算,其根本在于结构的边界条件是否与反应位移法的理论假设相吻合。对于暗挖隧道来说,周围的基岩或经过喷锚后的土体,在结构周围形成了一个壳体,相对于中间的空心结构来说,密度大,采用反应位移法计算是非常适合的,目前规范和文献中观点比较一致。但是对于明挖结构,其边界条件与施工方式有很大的关系,地基土、回填土的密实度、基坑支护形式等,对结构侧面边界条件的模拟影响很大,充分表明了结构的动力响应很大程度上是结构与土层的变形协调问题。
3 计算分析
基于上述对地下明挖结构抗震计算方法的选择问题,通过一个工程案例,来论述大型综合地下结构抗震计算的关键问题。明挖地下结构若采用闭合框架结构,抗震计算并不控制结构的内力,往往是结构上部的填土压力、侧向土压力等是结构的主要荷载。但是当闭合框架内部采用墩柱作为主受力构件时,抗震计算非常关键,墩柱将成为抗震计算关注的焦点。
雄安新区大型地下综合结构集综合管廊和物流于一体,地下一层为物流,为了达到两侧道路的通透性,两箱室之间设置墩柱,柱纵向间距采用6m,地下二层为4 舱室综合管廊。施工方式采用大开挖后填土,地面设有市政交通,结构覆土为4m ~7m。结构的抗震设防烈度为8 度,地震动峰值加速度为0.3g,地震动峰值位移为0.49m,场地类别为Ⅲ类。
地勘提供该场地的基床系数为30000kN/m3,地下16m处地层的压缩模量为13.6MPa,换算为剪切模量为26000kN/m2。结构断面如图3 所示,采用Midas-GEN软件对其建立空间模型见图4。
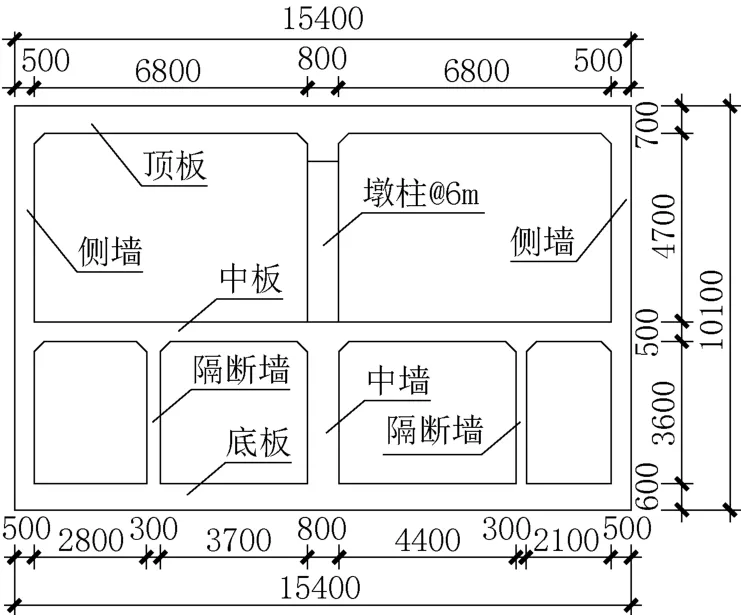
图3 大型综合地下结构断面(单位: mm)Fig.3 Section of large comprehensive underground structure(unit:mm)
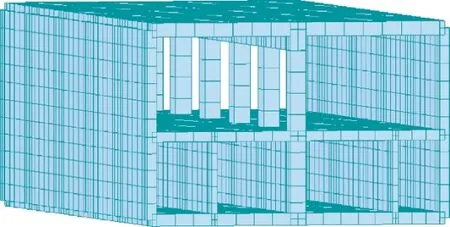
图4 大型综合地下结构计算模型Fig.4 Calculation model of large comprehensive underground structure
结构周围用地基的弹簧刚度模拟周围土体对结构的作用。文献[3]中给出剪切方向的弹簧刚度是径向刚度的1/3,文献[5]中给出的经验公式表明,在相同地质情况下,结构侧向水平的弹簧刚度是竖向弹簧刚度的0.4 ~0.6 倍,底板越宽倍数越小,仅作为经验值,不同的文献仍有不同的观点。但是地基弹簧刚度的大小对反应位移法计算的结果影响很大,实际计算中,还是要从实际的侧向土体约束情况出发,尽量真实地定义和模拟。本计算仅为寻求正确的计算方法而分别采用不同的侧向基床系数情况下,惯性力产生的墩柱弯矩和位移计算结果如图5 所示。
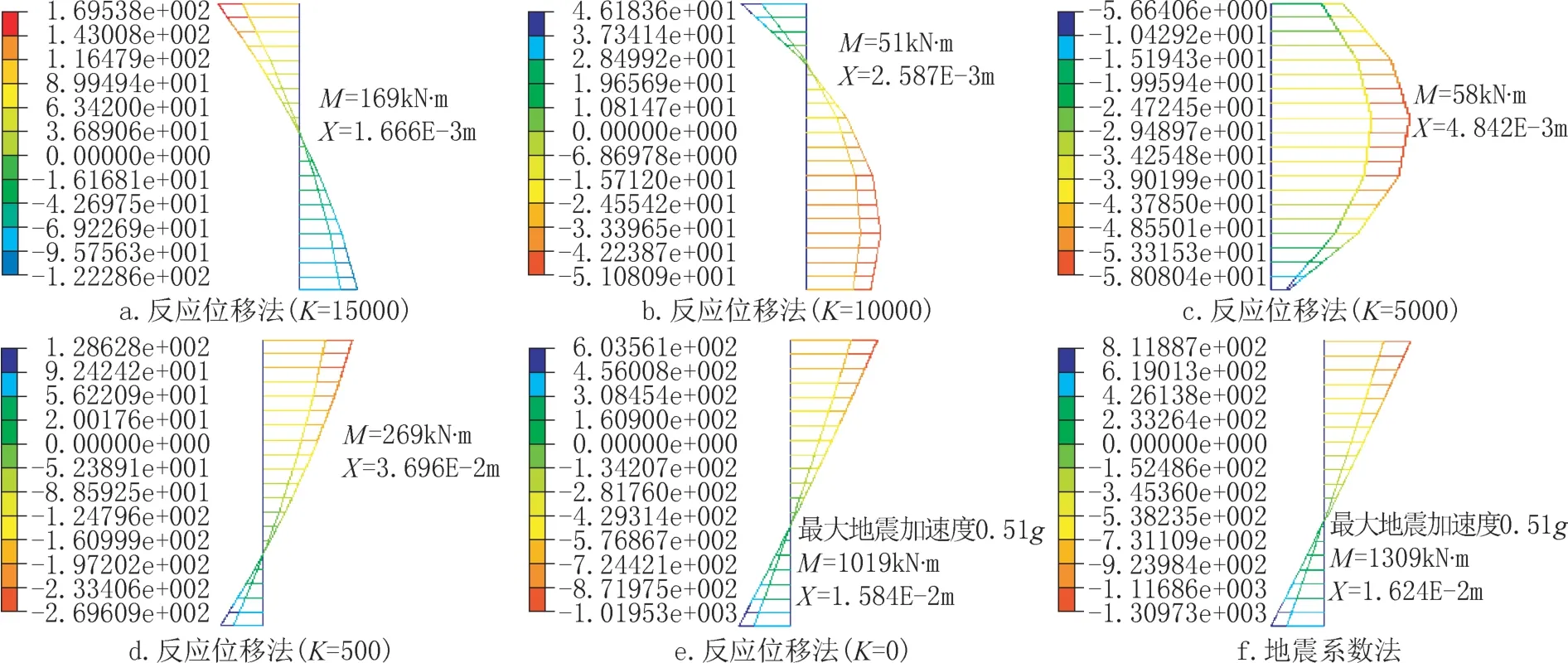
图5 对应不同侧面基床系数的反应位移法和地震系数法对惯性力作用下墩柱弯矩的影响对比Fig.5 Comparison diagram of influence of reaction displacement method corresponding to different side bed coefficients and inertia force method on bending moment of pier column
从图5a ~5c 可见,随着侧向基床系数的减小,惯性力产生的墩柱最大内力在减少,最大位移在增大,这是因为在采用反应位移法进行抗震计算中,当边界对结构的约束减弱时,结构连带边界共同的结构刚度降低,则结构的反应降低(由于篇幅原因,没有列出更多工况);当边界约束继续降低(图5c ~5d),此时结构逐渐表现出自身的自振特性,惯性力开始出现增大的趋势;当彻底去掉侧向约束(图5e),结构基本等同于地面结构,此时结构完全表现为自振特性,惯性力成为结构全部的地震反应。图5e 为采用反应位移法计算的惯性力响应,图5f为采用地震系数法计算的结构惯性力响应,为了计算对比,将二者的地震加速度取为相同的数值。由此可见,此时两种方法计算得到的惯性力结果接近,说明地下结构采用两种抗震计算方法计算结果的不同,主要在于结构与边界的变形协调问题,反应位移法更加适合地下结构的抗震计算,只是地下结构的侧向约束的取值尤为重要。
图6 一方面表达了在反应位移法的计算中,土层剪力、土层位移和惯性力三种地震力的作用结果,随着侧向基床系数的变化而变化的趋势。地震动施加于结构的土层位移和土层剪力,随着侧向基床系数的减少而减少,当侧向约束不足以有效传递土层剪力和土体变形时,其地震反应的特性不再与反应位移法的假定吻合,更多表现为结构的自振特性,适合采用地震系数法进行计算,与图5 的规律相一致,当约束接近消失时,结构接近地面结构,将完全表现为自振特性。
另一方面,从反应位移法的计算结果可见,反应位移法计算的地震响应中,土层剪力的作用最为显著,占比达到50%以上;其次是土体变形,约占结构响应的30%左右,而且土层变形对边界条件的依赖性更强;结构惯性力占比最小,通常低于10%。但是三者的占比,会随着侧向基床系数的取值而发生变化。
第三方面,在正常侧向约束的情况下,反应位移法计算的墩柱最大弯矩为2835kN·m(位移、剪力和惯性力共同作用的结果,见图6),完全没有侧向约束的地震系数法计算的结果为3082kN·m(由于篇幅原因,未列详细计算过程),对于具有侧向约束的地下结构,这样的计算结果还是与实际情况相吻合的。
4 结论
综上所述,大型综合地下结构的抗震计算采用的方法,主要取决于结构与土体的变形协调程度。如果侧向土体密度大,约束强,地震作用下结构的变形与土体的变形相协调,采用反应位移法进行抗震计算是比较合适的;如果侧面土体对结构的约束弱到大地的地震位移不能有效传递到结构上,或是地震发生时,地下结构与大地之间的位移特性不一致,主要表现为自振特性,则不适合采用反应位移法,采用地震系数法更为合适。
在抗震计算的有限元模型中,土体的侧向约束情况通常用侧向基床系数来体现,反应位移法计算结果的有效性,主要取决于结构侧向基床系数的取值。基床系数这个指标,不同的实验方法、实验条件以及不同的取值比例,其结果均会有较大的差别,这也成为很多学者质疑明挖地下结构采用反应位移法进行抗震计算的原因。所以基床系数的确定尤为重要,通常结合地勘提供的土层资料、经验公式综合判断确定。

