基于Ge2Sb2Se4Te1的可重构光开关的仿真

穆章健，李丽莹，杜 嘉，陈 楠，刘学静

（上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

光开关是集成光路上的一个基本元器件，起到把光动态切换到不同路径的作用。目前，片上光开关通常是基于电光或热光效应。但是以上两种效应产生的折射率差异均小于0.01，直接导致了设备的占用面积大且能耗增加。另外，由于这两种开关机制都是不稳定的，需要施加额外的源来维持光开关状态。

近几年，基于相变材料（phase change material，PCM）的片上光开关开始陆续出现[1]，相比传统的光开关它们有如下优势：1）在相变过程中能够形成巨大的光学调制特性和电阻率差异，如相变前后折射率差值大于1[2]，可以微化器件的结构；2）相变是非易失性的，即在晶态和非晶态的时候本身都比较稳定，不需要额外的能量来维持；3）在晶态和非晶态之间可实现ns级的快速转换；4）可实现多次稳定反复相变（可达1012个循环）。尽管基于相变材料的片开关具有这些吸引人的功能，但传统相变材料的高光吸收能力严重损害了现有基于相变材料的光开关的性能。两种最常用的相变材料是VO2和Ge2Sb2Te5（以下均简称为GST），它们即使在介电状态下，也会产生较高的光学损耗。比如，非晶态GST（与晶态相比具有较低的光学损耗）的消光系数k在1 550 nm波长处达到0.7，对应于42 000 dB/cm的衰减，这对于大多数导波设备应用来说是不可接受的。

GST是目前最常用的硫系相变材料，非晶态的透明波段在中、远红外，虽然适用操作波段宽至几十微米，但在通信波段附近，非晶态的GST依然有很强的吸收，这在集成光路中会造成明显的光损耗。品质因数（FOM）是有效折射率的差值（Δn）与消光系数（k）的比值，这一参数已被广泛用来衡量光开关的性能，并且被确认在光开关器件中与插入损耗和对比度定量相关[3-6]。按照定义，传统的相变材料总是受到低FOM的困扰，如在1 550 nm波长下GST和VO2的FOM分别大约是0.7和2.1。基于这些材料的光开关无论从理论上还是实验上均可得出在C波段（1 530～1 565 nm）下插入损耗（IL）达到2 dB或者更高，串口对比度（CT）小于15 dB，都表现出未优化的性能。

Zhang等[7]发现了一种的新型硫系相变材料Ge2Sb2Se4Te1（以下均简称为GSST），其来源于传统相变材料GST，即用Se取代部分Te[8]。新型材料在1 550 nm波长下，呈非晶态透明状，相变前后具有足够大的光学常数反差，有利于在激光器发出的强吸收波段下，诱导材料发生快速的可逆相变；各态稳定性好且可长期维持；材料本身易集成。根据对比FOM发现，GSST在通信波段1 550 nm处的FOM为4.2，大约是GST的2倍。而且在此波长下GSST非晶态的k值大约是非晶态GST的1/600，GSST晶态的k值为0.4左右，虽然比GST的要小，但是仍远超一般波导器件。

固体硫系相变材料发生相变需要加热到其融化温度或结晶温度，即当材料处于晶态时，想要切换到非晶态则需要给它加一个高能量的长脉冲使温度超过熔化温度，然后快速冷却使原本周期性排列的材料结构变为无序排列，当再给非晶态状态施加下一个低能量的长脉冲使温度超过晶化温度但小于熔化温度，并加热一段时间后，结构又会变回长程有序的周期性结构[9]。

本文提出了一种基于GSST的三波导定向耦合器式可重构光开关，通过有限元软件Lumerical来优化设计光开关在1 500～1 625 nm波段的光学特性，并利用多物理场仿真软件COMSOL对根据朗伯比尔定律采用激光加热的方式进行热学仿真。本文设计的光开关是一种可重构的光开关，可以重复多次切换，采用激光诱导相变的方式快速可行。

1 光学仿真

光定向耦合器是光学系统中的基础元件，在光分路器、光开关和光调制器等领域有着重要的应用价值[10]。最简单的传统定向耦合器由两个平行的矩形介质波导组成，当它们互相靠近达到耦合条件时，光功率就会在这两条波导间相互转移。本文设计的结构是2×2定向耦合器型的，共有三条波导组成，如图1所示，（a）为器件的俯视图，（b）为器件的侧面截图。

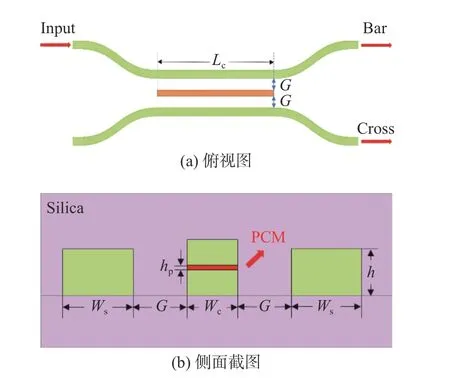
图1 2×2定向耦合器型光开关结构Fig.1 Structure of 2×2 directional coupler type switch

如图1所示的光开关结构是对称的，主要材料为氮化硅（SiN），而相变材料是中间SiN波导厚度hp为50 nm的埋层。SiN在红外波段1 500～1 625 nm处折射率n=2，消光系数k=0[11]。由于相变材料容易被氧化，整个结构需要埋在SiO2内。外侧SiN波导设定一样的中心高度h，然后通过参数扫描的方式优化出性能最佳时外侧SiN的宽度Ws、中间夹层波导的宽度Wc和外侧SiN波导与夹层波导之间距离G。

当GSST处于低损耗的晶态且外侧的SiN波导和中间夹层波导的模式有效折射率neff一致时，随着两条波导相互靠近，G会达到一个满足相位匹配条件的适当值，在此条件下根据超模理论，两波导之间会发生光耦合，即光强可以从一条波导传输到另外一条波导，这种现象被称之为“Cross”态。如果长度足够长，光强会在两条平行波导中往复传递，符合正弦函数规律。其中平行部分的长度Leff称为耦合长度，可以通过控制它从而控制输出端口的分光比。相反地，在高损耗的GSST晶态下，由于两个波导之间的巨大有效折射率差导致两种孤立模式，相位匹配条件失效，此时光只能在输入的那条波导内单向传输，这种现象被称之为“Bar”态。

图2为GST和GSST在近红外波段1 500～1 625 nm处的n、k对比。显然，与GST相比，GSST在两种状态下均显示出降低的光学损耗，在1 550 nm波长处的FOM要优于GST。

图2 GST与GSST在1 500～1 625 nm波段下非晶态和晶态的n、kFig.2 n and k of GST and GSST in amorphous and crystalline states at 1 500-1 625 nm

首先把GSST此波段下非晶态和晶态的n、k导入到Lumerical软件中的Mode Solutions模块，SiN的高度均设置为450 nm，在宽度400～800 nm内扫描波导本征模下的有效折射率neff，结果如图3所示。

图3 波导有效折射率和宽度之间的关系Fig.3 Relation between effective refractive index and width of waveguides

从图3可以看出，GSST在晶态时中间夹层波导的neff要高于单条SiN的neff和GSST处于晶态时夹层波导的neff。根据超模理论，当两个相同的波导弱耦合时，每个超模都可以表示为两条波导支持的两个模态场的叠加。耦合到一个波导中的光可以视为对称和反对称超模的线性组合。这两个超模在传播过程中会产生相位差（由于它们的传播常数不同），从而导致波导之间的能量交换。如果两个波导的厚度和宽度不完全相同，相速度就会不同，但这种差异不一定会破坏耦合效果。如果相位差别很小，功率转移仍然可以发生，但是能量转移不完全。在非晶态下选择合适的宽度可以使单条SiN波导和夹层波导neff相同从而满足相位匹配条件，产生相同的传播常数。根据扫描的结果选择Ws=664 nm、Wc=420 nm，可以在GSST非晶态下实现外侧单条SiN波导和中间夹层波导的neff一致，满足相位匹配条件。再用Mode Solutions分别对夹层波导在GSST晶态与非晶态下进行模场计算，结果如图4所示。

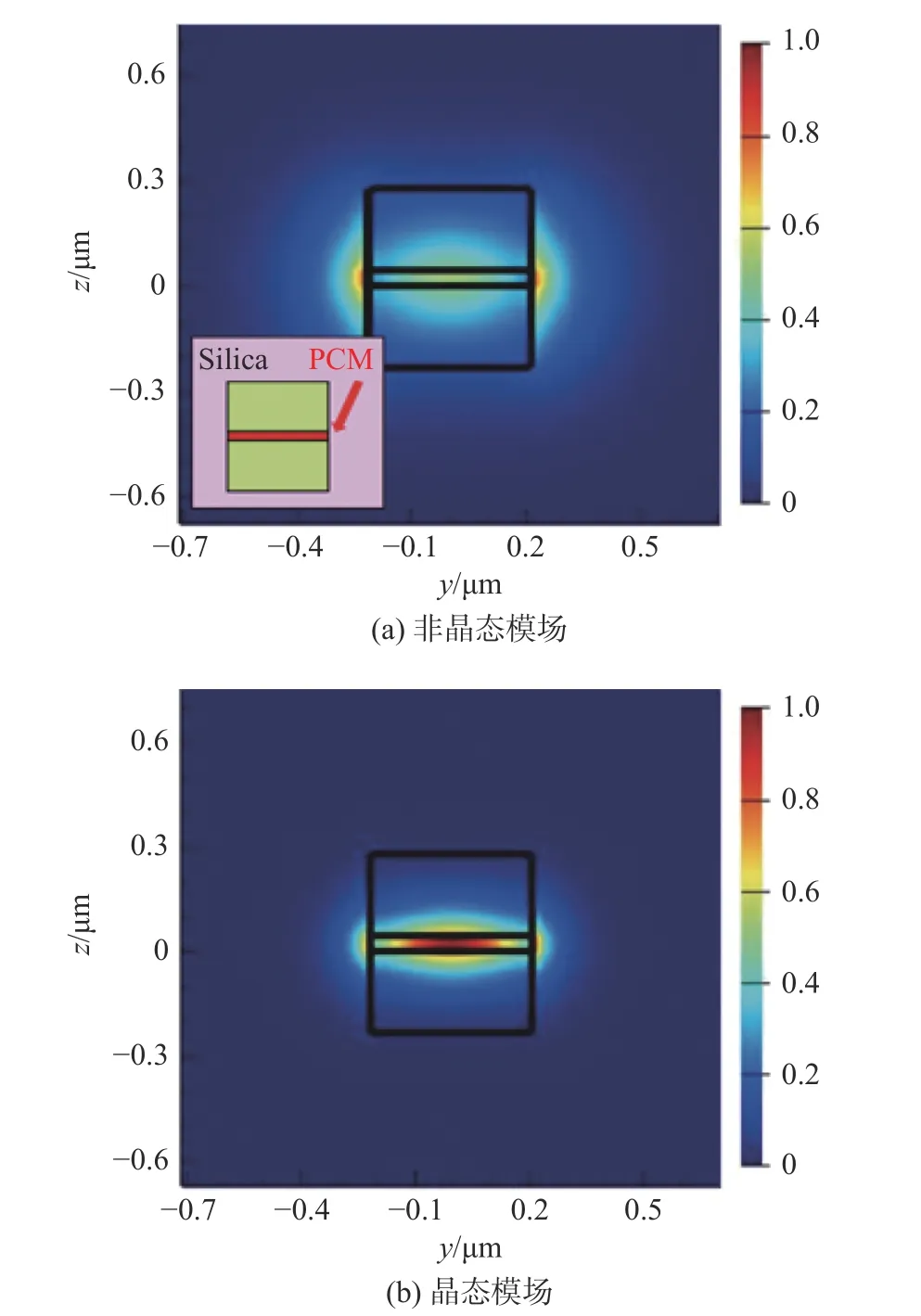
图4 夹层波导的模场仿真Fig.4 Simulation of mode field of sandwich waveguide

通过仿真可知，GSST在非晶态下夹层波导neff为1.615+（1.4×10−4）i，而在晶态下neff为2.19+0.21i，对比形成了较大的neff差异。再利用FDTD Solutions模块设计结构，边界条件选择完全匹配层（PML），网格尺寸最小化到10 nm。TE和TM模式均能在此结构下工作[12]，但由于TM模式更有利于低损耗的光开关，因此输入光源选择TM模式[13]。在1 550 nm波长下依据插入损耗（IL）和输出串口对比度（CT）为评价参数扫描优化，发现当G为515 nm对应的Lc长度为24.9 μm时光开关的特性最好，此时器件满足了相位匹配条件。在1 550 nm波长GSST非晶态的时候IL为−0.013 dB，CT为−41.56 dB；晶态下IL为−0.33 dB，CT为−34.61 dB。仿真得到的光开关光场分布如图5所示。

从图5可以看出，波长在1 550 nm非晶态时输入光可以从上面的波导通过耦合完全传入到下面的输出端口；在晶态时，光则只能在上面波导单向传输而不能耦合到下面波导，这实现了光开关的作用。把波段扩展为1 500～1 625 nm，对以上结构再次进行仿真，得到IL、CT分别和波长对应的关系，结果如图6所示。

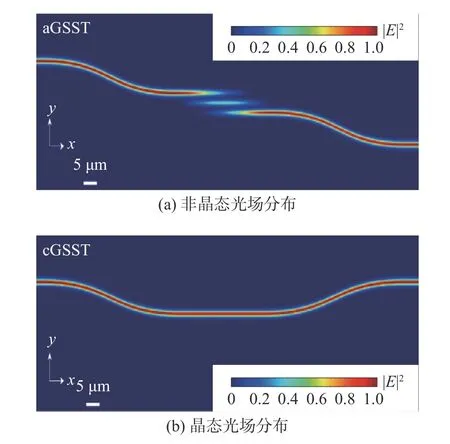
图5 在1 550 nm波长下仿真的光场分布Fig.5 Simulations of light field distribution at 1 550 nm

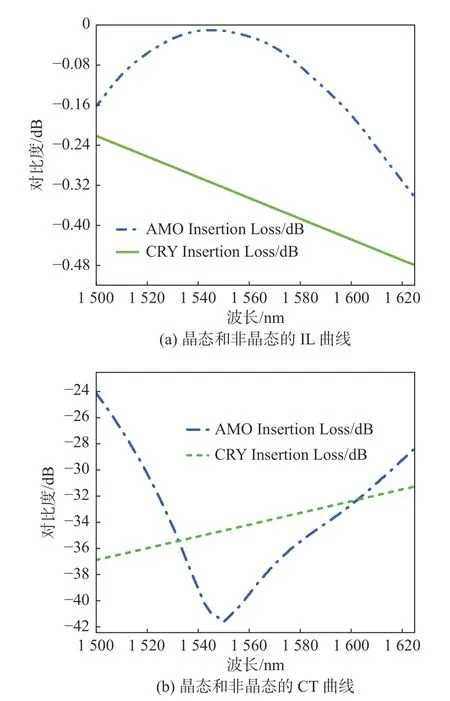
图6 1 500～1 625 nm波段光开关的IL和CT曲线Fig.6 IL and CT curves of switch across 1 500-1 625 nm band

图6显示了设计的光开关在1 500～1 625 nm波段GSST非晶态下ILs＞−0.36 dB，CTs＜−24 dB；GSST晶态下ILs＞−0.44 dB，CTs＜−30.46 dB。无论是在非晶态还是晶态，都表现出小于1 dB的低ILs，具有较宽的带宽。Xu等[12]设计了一款基于GST的同类型光开关，在1 510～1 540 nm波段内晶态和非晶态下ILs均大于−1 dB，而在非晶态下CTs小于−15 dB，晶态下CT小于−20 dB。对比可以发现基于GSST的定向耦合器型光开关的性能小于基于GST型的，这是由于在红外波段，GSST的消光系数k远小于GST的。与Liang等[13]同样采用GST的设计的不同结构光开关器件相比，本文设计的器件一样具有显著的优势。与Zhang等[2]设计的基于GSST的光开关相比，本文设计的光开关在1 550 nm波长下IL很接近，但是在非晶态和晶态下的CT值显得更具有优势，这是由于TM模式更适合2×2式的定向耦合器型光开关。本文设计的光开关耦合长度要远小于其器件，这对于集成光路的微型化发展来说更具有优势。

2 热学仿真

一束高强度的激光入射到半透明的材料内，能量将沉积在材料本身，经吸收转化成热量，导致波导的热场发生变化[14]。利用上一节设计的光开关结构并借助多物理场仿真软件COMSOL进行热场仿真，研究了利用激光加热诱导GSST发生相变模型的可行性。

假设入射光为一束平行入射的单波长激光，且在材料中经历较少的折射、反射或散射，便可以用朗伯比尔定律来模拟光强。对于光强I，可以将这一定律写为微分形式，即

式中：z为沿光束方向的坐标；α为材料的吸收系数。由于温度会随着空间和时间发生变化，还需要求解有关材料内温度分布的控制偏微分方程

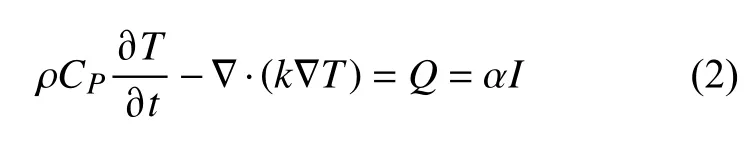
式中：Q为热源项，等于吸收的光；ρ、CP和k分别为材料的密度、恒压热容与导热系数。式（1）与式（2）代表了一个双向耦合多物理场。

通过查阅相关文献[13-18]，得知GSST、SiN和SiO2的热学系数，结果如表1所示。

表1 用于热仿真的系数Tab.1 Coefficients used for the thermal simulation

从晶态（C-）到非晶态（A-）需要一个高能量的短脉冲使GSST的温度超过熔化温度900 K，然后快速冷却使原子排列从有序转成无序；从非晶态转化到晶态则需要一个低能量的长脉冲，缓慢加热温度超过523 K并低于900 K持续一段时间使原子排列从无序转成有序。

定义一束波长为532 nm的激光从器件正上方垂直入射，其中光束半径越大，则GSST薄膜温差越小，但所需能量增加；半径越小中心能量越高，温差就越大，造成中心发生灼穿但边缘却还未熔化的现象。此外，还需考虑薄膜深度上的温度差异。因此，合适的光束半径与入射功率对材料相变成功与否至关重要。

为了讨论GSST由晶态转化为非晶态的过程：首先，在COMSOL中输入一个高能量的高斯短脉冲，脉宽设为25 ns，网格选择极细化；然后，分别以GSST薄膜上表面和下表面中心为原点沿长度方向每隔1 μm插入温度探针；最后，输入双向耦合公式并建模，进行功率和半径的扫描。结果发现，在光斑半径为29 μm、峰值功率为45 mW的时候能够满足GSST整体同时达到熔融状态并且不会出现灼穿的情况。仿真结果如图7、图8所示。

图7为器件的体温度和截面温度分布情况，热场的分布情况能够被直观地观察。扫描结果表明，峰值功率为45 mW、半径为29 μm的532 nm激光可以引起24.9 μm长的GSST薄膜完全发生非晶化过程。从图8可以看出：GSST薄膜在同一层的中心温度要高于周围温度，分布呈高斯状；顶部和中间部分温度首先超过融化值并发生非晶化过程。

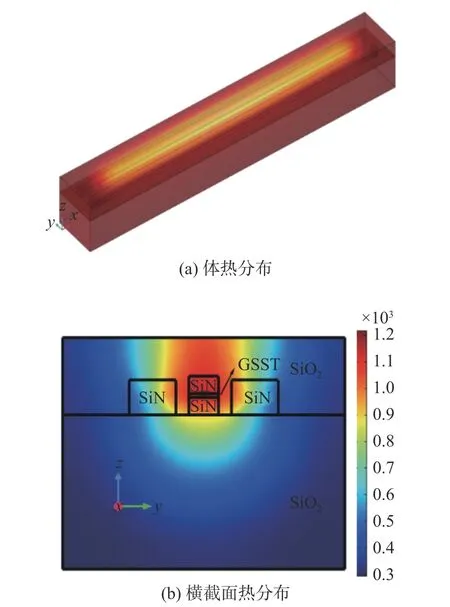
图7 激光加热分布情况Fig.7 Distribution of laser heating

图8 GSST层的上下温度分布Fig.8 Temperature distribution of top and bottom GSST layer

为了诱导再结晶，需要将GSST加热到523 K以上但低于900 K，并加热一段时间。虽然温度低于熔化温度，但这一过程更复杂一些。与非晶化只需要一个高斯脉冲不同，晶化过程需要脉冲阵列来完成。因此本文采用了峰值功率20 mW、周期1 μs和占空比0.03%（30 ns）的高斯脉冲阵列，并把GSST层内的最高温度和最低温度与时间建立函数。结果发现：经过一段脉冲阵列加热后，最高温度和最低温度均能满足高于晶化温度并低于融化温度；同一时间下最高温度与最低温度差值小于100 K，证明了从非晶态到晶态的转变可行，而且需要较低的能量。

3 结 论

本文对片上基于GSST可重构光开关在TM模式下进行了理论设计和分析。该开关由对称三波导耦合器组成，在1 500～1 625 nm内分别通过将GSST设置在非晶态或晶态来诱导“Cross”或“Bar”态。GSST在非晶态下器件IL＞−0.36 dB，CT＜ −24 dB；GSST在晶态下IL＞ −0.44 dB，CT＜−31.2 dB。关于切换条件，发现一个功率45 mW、脉宽25 ns的短激光脉冲可以使GSST整体温度超过900 K从晶态完全转化到非晶态；想要实现从非晶态到晶态的完全转化，可以施加多个功率20 mW、周期1 μs和占空比0.03%的脉冲阵列使整体温度超过523 K。设计的光开关可作为构建块组装Benes网络，可以实现任意复杂度级别的网络。