基于Contourlet域自适应Wiener阈值的同时震源波场分离
王坤喜, 毛伟建
1 中国科学院精密测量科学与技术创新研究院计算与勘探地球物理研究中心; 大地测量与地球动力学国家重点实验室, 武汉 430077 2 中国科学院大学, 北京 100049
0 引言
同时震源采集技术,也称多震源地震数据混合采集技术,可以在常规采集一个单炮地震记录的时间内采集多个炮的地震记录.当施工的周期不变时,通过增加激发的震源数量,提高对地下构造的覆盖次数,改善对地下构造的照明质量;当对目标区域的覆盖次数不变时,多个分布在不同区域的震源同时激发,可以大大缩短施工周期,提高采集效率(Li et al.,2013;Zu et al.,2017;张攀和毛伟建,2018).由于相邻震源之间的干扰会产生“混合噪声”,同时震源数据不能直接用于传统地震数据处理流程,需要先将混叠波场进行分离处理,得到常规的单炮数据.分离方法通常可以分为被动分离和主动分离两大类(Akerberg et al.,2008;Liu et al.,2014;Magnussen,2015).
被动分离是将分离问题转换为去噪问题,将经过延迟时间编码的干扰炮信号视为噪声.当不同震源之间存在随机时间差时,混合噪声在非共炮域(如共检波点域、共中心点域、共偏移距域等)不再具有连续性,表现为伪随机脉冲,而有效信号仍然保持连续相干性(Doulgeris et al.,2012).基于上述性质,Moore等(2008)在共偏移距道集进行滤波分离.Huo等(2009)利用多方向矢量中值滤波法对地层的倾角进行了扫描,求得最佳倾角方向后利用中值滤波去除共中心点域的混合噪声.Kim等(2009)基于数据本身建立了一个噪声估计模型,然后从采集数据中自适应的提取噪声,该算法适用于共炮检距道集.Zhang和Olofsson(2012)采用加权τ-p变换压制邻炮干扰.Yang等(2017)提出先用PWD(plane-wave destruction)求取地层的倾角信息,再结合矢量中值滤波对串扰噪声进行压制.
另一种分离类方法是主动分离,也被称为反演类方法,该方法是将分离问题提炼成数学中的反问题,利用反演类方法进行求解.Akerberg等(2008)、Moore(2010)和刘强等(2014)在Radon域进行了稀疏约束下的迭代反演分离.Lin和Herrmann(2009)在Curvelet域进行稀疏表示,利用压缩感知对混合的波场进行分离.Abma等(2010)在频率域通过稀疏约束的POCS(projection onto convex sets)方法使不相干信号能量最小化,进而获取分离信号.Tan等(2013)基于互易定理,利用稀疏反演的方法进行波场分离.Chen等(2014)提出整形正则化反演的方法并在Seislet域利用阈值进行约束反演.祖绍环等(2016)在Curvelet域进行稀疏约束,同样利用阈值进行约束反演.宋家文等(2019)将地震数据转换到频率—波数—波数域(FKK),提出了一种高效混采数据分离的方法.在稀疏迭代分离框架下,除了使用固定的变换域外,一些学者也考虑采用字典学习来完成分离(Chen,2017;Zhou et al.,2017),但是字典学习的方法需要很大的计算开销.
在同时震源稀疏域迭代反演中,选择一个合适的稀疏基十分重要,它决定了分离效果和迭代收敛的速度.Do和Vetterli(2002)首次提出了Contourlet变换理论,将拉普拉斯金字塔(Burt and Adelson,1983;Do and Vetterli,2003)和二维方向滤波器组串联在一起组成金字塔多方向滤波器组(Do and Vetterli,2001),可以将信号数据分解成不同尺度下的方向子带,很好地抓住数据的几何结构特征,满足曲线的各向异性尺度关系,能够快速并结构化分解采样信号.Contourlet变换将多尺度分析和方向分析分开进行,首先由拉普拉斯金字塔变换对图像进行多尺度分解以“捕获”点奇异,接着由方向滤波器组将分布在同方向上的奇异点合成一个系数.Contourlet变换的最终结果是用类似于线段的基结构来逼近原图像,相对于Wavelet变换和Curvelet变换等多尺度分析工具,Contourlet变换具有更少的冗余度和更好的逼近性能,因此Contourlet变换已在信号处理、图像处理等领域得到广泛应用,如信号去噪(Eslami and Radha,2003),目标检测(Wilbur et al.,2009),图像压缩(Chang et al.,2000a)等等.
与数字图像去噪的目标相似,同时震源的稀疏域迭代反演分离需要在去除串扰噪声的同时尽可能地保留地震数据中的弱信号和细节信息(Zu et al.,2017),合理地选取阈值非常重要,直接影响到分离效果(Yang et al.,2013).Donoho和Johnstone(1994)在小波域提出了阈值收缩方法,给出了Universal阈值,并从渐进意义上证明了Universal阈值的最优性(Donoho,1995),然而Universal阈值是阈值的上限,但不是最佳收缩阈值,它过度“扼杀”了小波系数,丢失信号的细节部分.Donoho和Johnstone(1995)又提出了SURE阈值,但是该阈值偏于保守,在信噪比很小的情况下,其效果不如Universal阈值.Zhang和Desai(1998)改进SURE阈值提出了SureShrink阈值,可以求出理想阈值的估计值,但没有显式表达式,阈值的计算往往需要预先知道信号本身,但实际求取中这是不可能的.Chang等(2000a)假设原始不带噪声信号在小波域的系数服从广义高斯分布,在贝叶斯框架下通过最小化贝叶斯风险,得到了著名的BayesShrink阈值,该阈值考虑了信号在小波域的先验知识,具有很好的去噪效果.在借鉴图像压缩编码中的上下文模型方法后,Chang等(2000b)又提出了具有局部自适应能力的BayesShrink阈值,能够灵活实现去噪与保留信号之间的平衡.在贝叶斯最大后验概率估计理论下,Moulin和Liu(1999)假设图像子带的小波系数服从拉普拉斯分布或者高斯分布,可以分别推导得到MapShrink阈值与Wiener阈值,这两个阈值算子都具有较好的去噪效果.
以上阈值方法的提出主要用于数字图像去噪中,一些学者也在研究适用于同时震源稀疏域迭代反演分离的阈值算子.Chen等(2014)提出在Seislet域采用百分位法(Yang et al.,2013)分段设置硬阈值,取得了一定的分离效果,后来又在PNMO-MF-FK联合滤波器下使用线性衰减硬阈值也得到了较好的分离结果.该阈值算子在初始迭代时取系数最大值,并随着迭代次数线性衰减为零(Chen et al.,2015).Li等(2018)将混叠数据变换到Curvelet域后,发现相干信号主要集中在低频子带中,串扰噪声主要集中在高频子带中,通过考虑在不同子带设置不同的阈值,取得了比全局一致方法更好的效果.Zu等(2018)将该阈值方法推广并运用于三维同时震源数据分离.在同时震源稀疏域迭代反演分离方法中,另一种常见的阈值是指数衰减阈值(Gao et al.,2010;Cheng and Sacchi,2015;Song et al.,2019).与常数和线性衰减阈值相比,指数衰减阈值具有更快的收敛速度,但是该阈值没有充分利用稀疏域系数的分布情况等先验信息,不具备自适应去噪的能力.
本文利用Contourlet变换良好的稀疏表达能力,通过稀疏域阈值收缩来迭代反演分离同时震源数据.我们在子带一致的Wiener阈值基础上做出改进,提出具有尺度与空间自适应的Wiener阈值.通过两个模拟数据和两个实际数据的应用结果验证本文提出的自适应Wiener阈值方法的有效性.
1 方法
1.1 稀疏迭代反演分离
在时间域,每个检波点接收到的同时震源混合记录可表示为
(1)
其中dobs为混叠道集记录,db为第b个震源的原始道集记录,m为混叠度.对角矩阵Γb表示第b个震源的延迟时间矩阵,其表达式为
Γb=F-1diag(e-iω tb,1,e-iω tb,2,…,e-iω tb,u,…)F,
(2)
其中,tb,u为第b个震源第u道激发的延迟时间,i为虚数单位,ω为角频率,F和F-1表示一对正逆傅里叶变换.通常,在同时震源数据分离中,第一个震源(本文称为主炮)的延迟时间算子(Γ1)为单位矩阵I,得到连续相干的有效信号;其他震源(本文统称为干扰炮)在延迟时间算子的作用下会形成串扰噪声.
同时震源数据的稀疏反演分离问题可以表示如下:
(3)
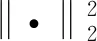
求解式(3)的一个常用迭代框架是非线性整形正则化框架(Chen et al.,2014):
(4)
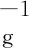
S=C-1TC,
(5)
其中T为阈值参数,C和C-1分别代表稀疏变换及其逆变换,本文中C为Contourlet变换.
共检波点道集或共偏移距道集中的主炮信号在Contourlet域是聚焦的能量点,而干扰炮信号是分散的串扰噪声,T可以对变换域系数进行收缩从而有效地压制串扰噪声进而分离混叠波场.因此,同时震源数据的稀疏迭代反演分离的关键是如何确定合适的T.
1.2 子带一致Wiener阈值
在每一次迭代下使用阈值T进行收缩去噪前,主炮信号一般是连续相干的,干扰炮信号在延迟时间作用下会以串扰噪声的形式存在,所以此时分离问题可以看作噪声去除问题:
Y=X+N,
(6)
其中Y、X和N分别表示变换域中包含噪声的混叠数据、不含噪声的原始主炮数据和串扰噪声数据.在每一次迭代中,混叠数据在Contourlet域被分解为K层,每层L个方向,用k=1,2…,K表示分解的第k个尺度,频率越高k越大;用l=1,2…,L表示第k个尺度的方向数.在Contourlet域,假设原始主炮数据和串扰噪声数据的各方向子带系数都服从高斯分布,根据贝叶斯最大后验概率估计理论,可以求得Wiener滤波公式(Moulin and Liu,1999)
(7)
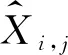
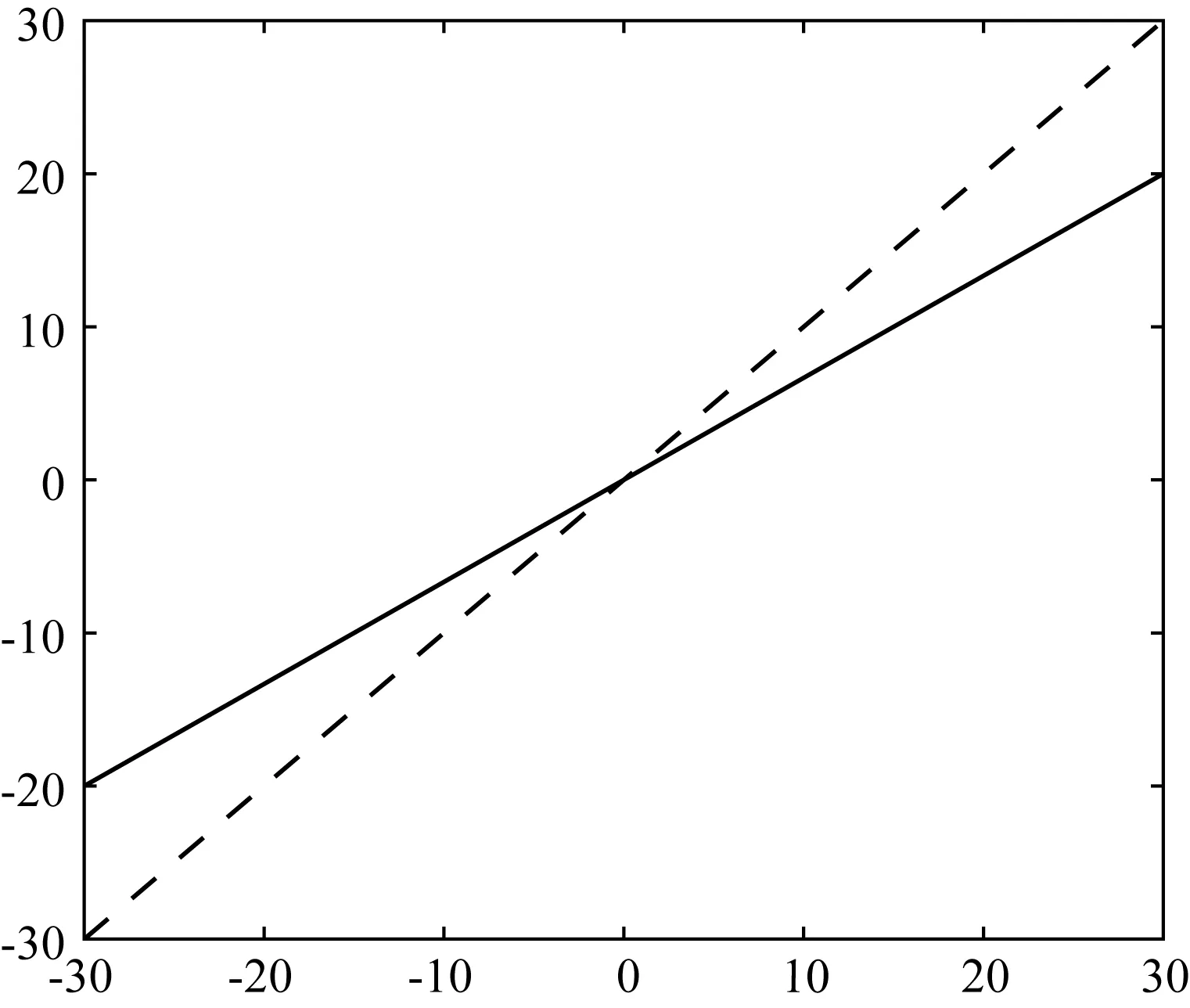
图1 Wiener阈值收缩函数形式示意图Fig.1 Schematic diagram of the Wiener threshold contraction function
由Wiener阈值收缩原理(式(7)),可得Wiener阈值
(8)
式(8)中σN可以采用鲁棒中位数估计法(Donoho and Johnstone,1994,1995)求取
(9)
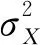
(10)
其中Num为Yi,j所处子带的全部系数个数.
1.3 自适应Wiener阈值
子带一致阈值法能够取得一定的分离效果,但是由于没有考虑到串扰噪声在Contourlet域中不同尺度的分布规律以及有效信号的空间分布规律,该方法在串扰噪声的压制效果、有效信号尤其是弱信号的保留和迭代收敛速度方面存在不足.基于以上考虑,我们分别从噪声方差计算和有效信号方差计算两个方面进行改进,获得自适应Wiener阈值.
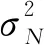
(11)
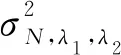
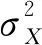
(12)
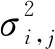
根据式(11)与式(12),改进后的尺度与空间自适应Wiener阈值算子可以表示为
(13)
在Contourlet域使用式(13)的阈值算子迭代反演分离同时震源数据的方法称为Contourlet域自适应Wiener阈值法,下文简称为自适应阈值法.
2 算例
2.1 Marmousi模型数据
Marmousi模型是石油工业界用于方法测试的一个复杂地质模型.图2a和图2b分别为主炮和干扰炮激发采集的未混叠共检波点道集数据,共767道;图2b数据在0~1 s随机延迟时间作用下以伪随机噪声的形式加到主炮波场中,形成如图2c所示的混叠波场,混叠度m=2.模拟计算在Intel Xeon E7-4807、内存为128G的IBM服务器上展开,没有并行计算.Contourlet变换选择“9-7”塔式分解滤波器和“pkva”方向滤波器进行三层分解,方向数分别为4、8和8.在本次测试的自适应Wiener阈值算子中,α的取值为0.6.图3a—b分别为图2a数据与图2c数据在Contourlet域中不同尺度不同方向的系数分布情况,可以看出在迭代初期,有效信号的系数集中分布在中低频部分,而串扰噪声的系数主要分布在中高频部分.图4a为图2a数据在Contourlet域中不同尺度不同方向的系数统计分布直方图,可以看出系数多集中分布在零点附近,形态上表现为尖峰长尾,可以用高斯分布来逼近,当分解的尺度越低,得到数值较大的系数越多,进一步证明了连续相干的有效信号集中分布于低频和中频子带中;图4b为串扰噪声数据在Contourlet域中不同尺度不同方向的系数统计分布直方图,可以看出串扰噪声分布满足高斯模型,且数值较大的系数多集中存在于中高频子带中.
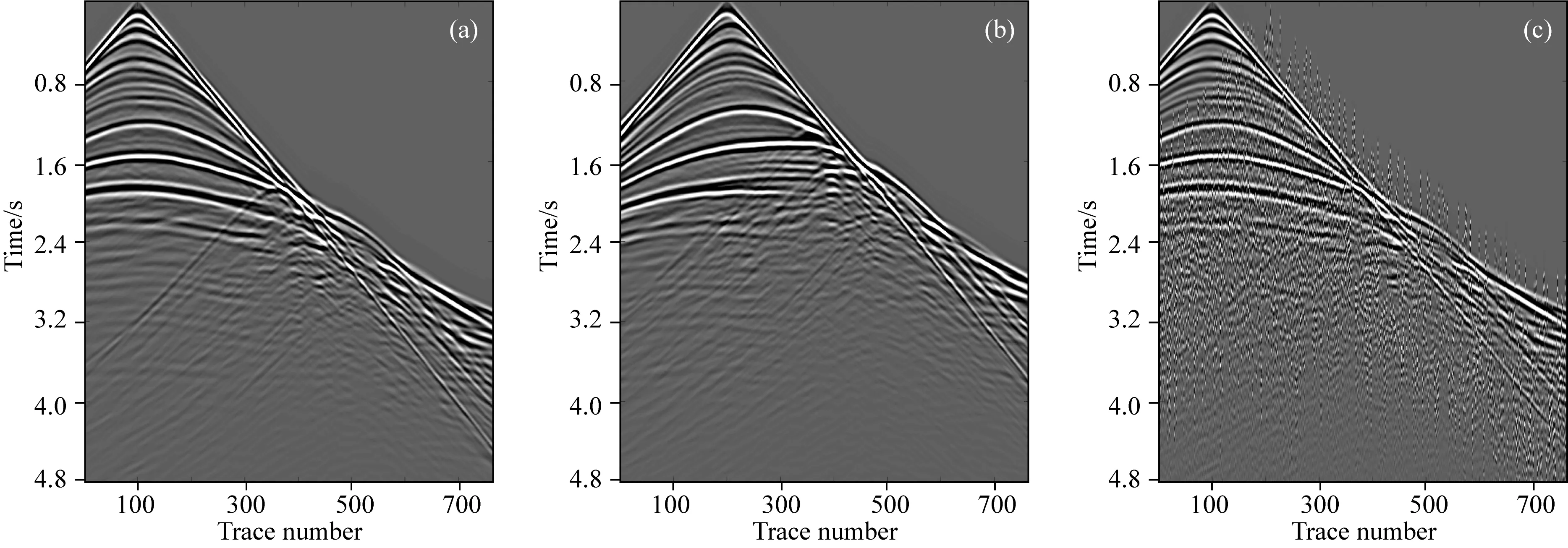
图2 Marmousi模型中共检波点道集数据 (a) 原始主炮数据; (b) 原始干扰炮数据; (c) 混叠数据.Fig.2 Data of Marmousi model in common receiver domain (a) Original data of the main source; (b) Original data of the interference source; (c) Blended data.

图3 Contourlet域不同尺度不同方向分解的子带系数分布图 (a) 原始主炮数据; (b) 混叠数据.Fig.3 Distribution of subband coefficients in different scales and different directions in Contourlet domain (a) Original data of the main source; (b) Blended data.

图4 Contourlet域的不同尺度不同方向子带系数统计分布直方图 (a) 原始主炮数据; (b) 串扰噪声数据.Fig.4 Statistical distribution histogram of subband coefficients in different scales and different directions in Contourlet domain (a) Original data of the main source; (b) Crosstalk noise data.

图5 不同方法分离主炮的结果和放大10倍的残差 (a) 子带一致阈值法分离结果; (b) Curvelet域指数衰减阈值法分离结果; (c) 本文提出的自适应阈值法分离结果; (d)、(e)和(f)分别是分离结果(a)、(b)和(c)所对应的残差(已放大10倍).Fig.5 Deblended results of the main source from different methods and corresponding residuals with 10 times scaled up (a) Deblended result from the subband consistent threshold method; (b) from the exponential attenuation threshold method in Curvelet domain; (c) from the proposed adaptive threshold method; (d), (e) and (f) are the residuals with 10 times scaled up corresponding to the results (a), (b) and (c), respectively.
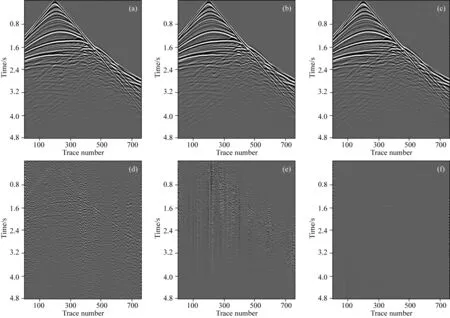
图6 不同方法分离干扰炮的结果和放大10倍的残差 (a) 子带一致阈值法分离结果; (b) Curvelet域指数衰减阈值法分离结果; (c) 本文提出的自适应阈值法分离结果; (d)、(e)和(f)分别是分离结果(a)、(b)和(c)所对应的残差(已放大10倍).Fig.6 Deblended results of the interference source from different methods and corresponding residuals with 10 times scaled up (a) Deblended result from the subband consistent threshold method; (b) from the exponential attenuation threshold method in Curvelet domain; (c) from the proposed adaptive threshold method; (d), (e) and (f) are the residuals with 10 times scaled up corresponding to the results (a), (b) and (c), respectively.
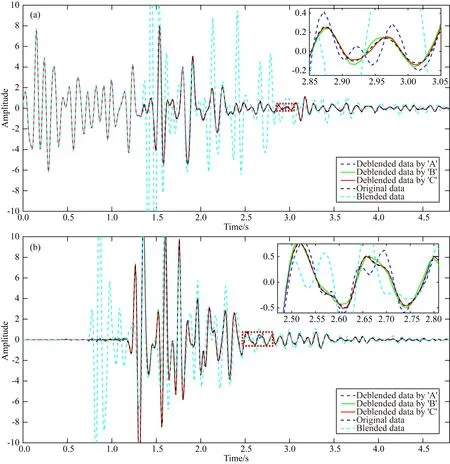
图7 原始主炮数据、混叠数据和用三种分离方法得到的分离后主炮数据的单道波形对比图 右上角子图为红色虚线矩形框的放大图,‘A’表示子带一致阈值法,‘B’表示Curvelet域指数衰减阈值法,‘C’表示本文提出的自适应阈值法. (a) 图2a、图2c和图5a—c中第110道数据; (b) 图2a、图2c和图5a—c中第300道数据.Fig.7 The single trace waveform comparison of the original data, blended data, and deblended data from the three deblending methods for the main source The upper right subgraph is the zoomed-in section of the red rectangle box. ‘A’ is for the subband consistent threshold method, ‘B’ for the exponential attenuation threshold method in Curvelet domain, and ‘C’ for the proposed adaptive threshold method. (a) The 110th trace in Fig.2a,Fig.2c and Figs.5a—c; (b) The 300th trace in Fig.2a,Fig.2c and Figs.5a—c.
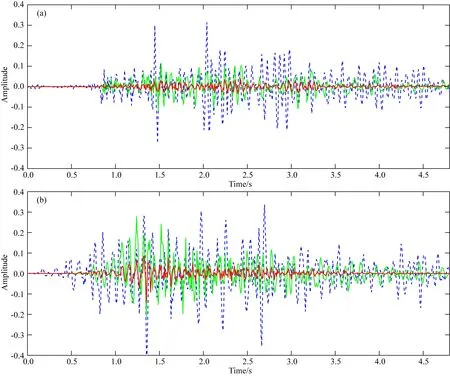
图8 三种分离方法得到单道分离误差对比图 蓝色虚线表示子带一致阈值法分离得到的误差,绿色实线表示用Curvelet域指数衰减阈值法分离得到的误差,红色实线表示 本文自适应阈值法分离得到的误差. (a) 图5d—f中第110道数据; (b) 图5d—f中第300道数据.Fig.8 A comparison of the errors for deblended single trace obtained from the three deblending methods The blue dotted line is the error for the subband consistent threshold method, the green solid line for the exponential attenuation threshold method in Curvelet domain, and the red solid line for the proposed adaptive threshold method. (a) The 110th trace in Figs.5d—f; (b) The 300th trace in Figs.5d—f.
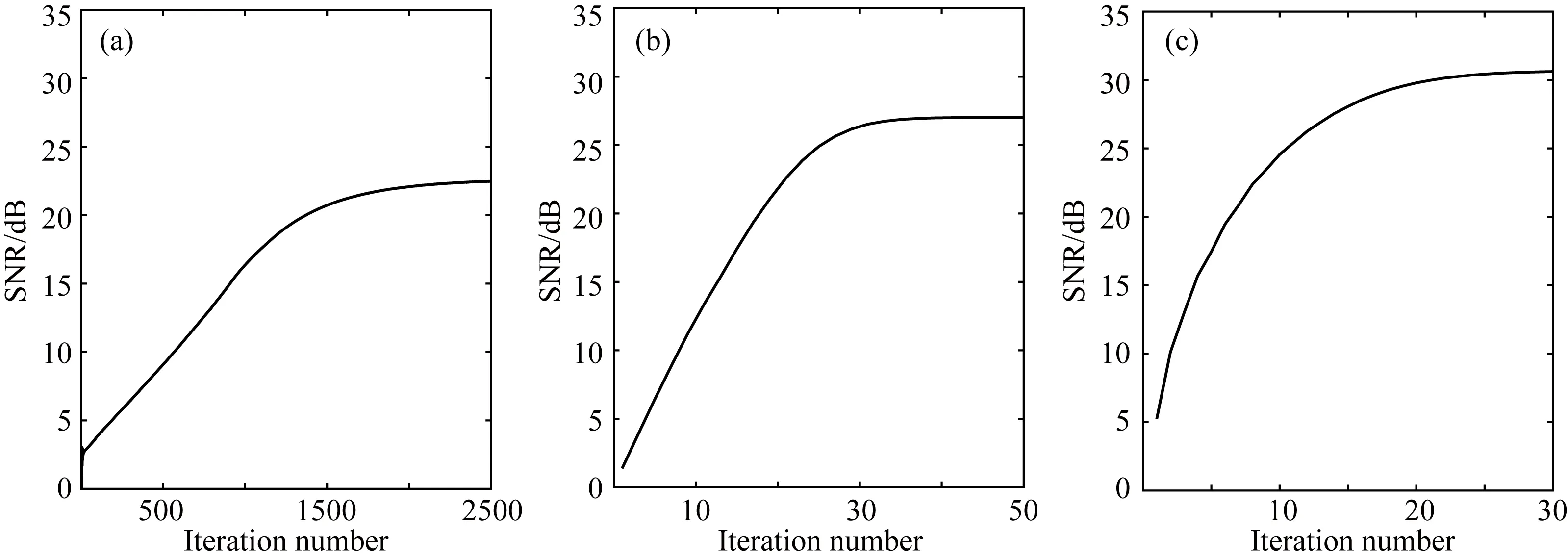
图9 不同分离方法处理Marmousi模型数据的分离信噪比曲线 (a) 子带一致阈值法; (b) Curvelet域指数衰减阈值法; (c) 本文提出的自适应阈值法.Fig.9 The SNR of the Marmousi model data from the different deblending methods (a) The subband consistent threshold method; (b) The exponential attenuation threshold method in Curvelet domain; (c) The proposed adaptive threshold method.
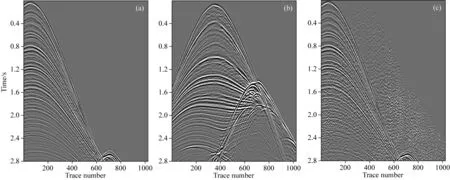
图10 SEAM模型数据 (a) 原始主炮数据; (b) 原始干扰炮数据; (c) 混叠数据.Fig.10 Data of the SEAM model (a) Original data of the main source; (b) Original data of the interference source; (c) Blended data.
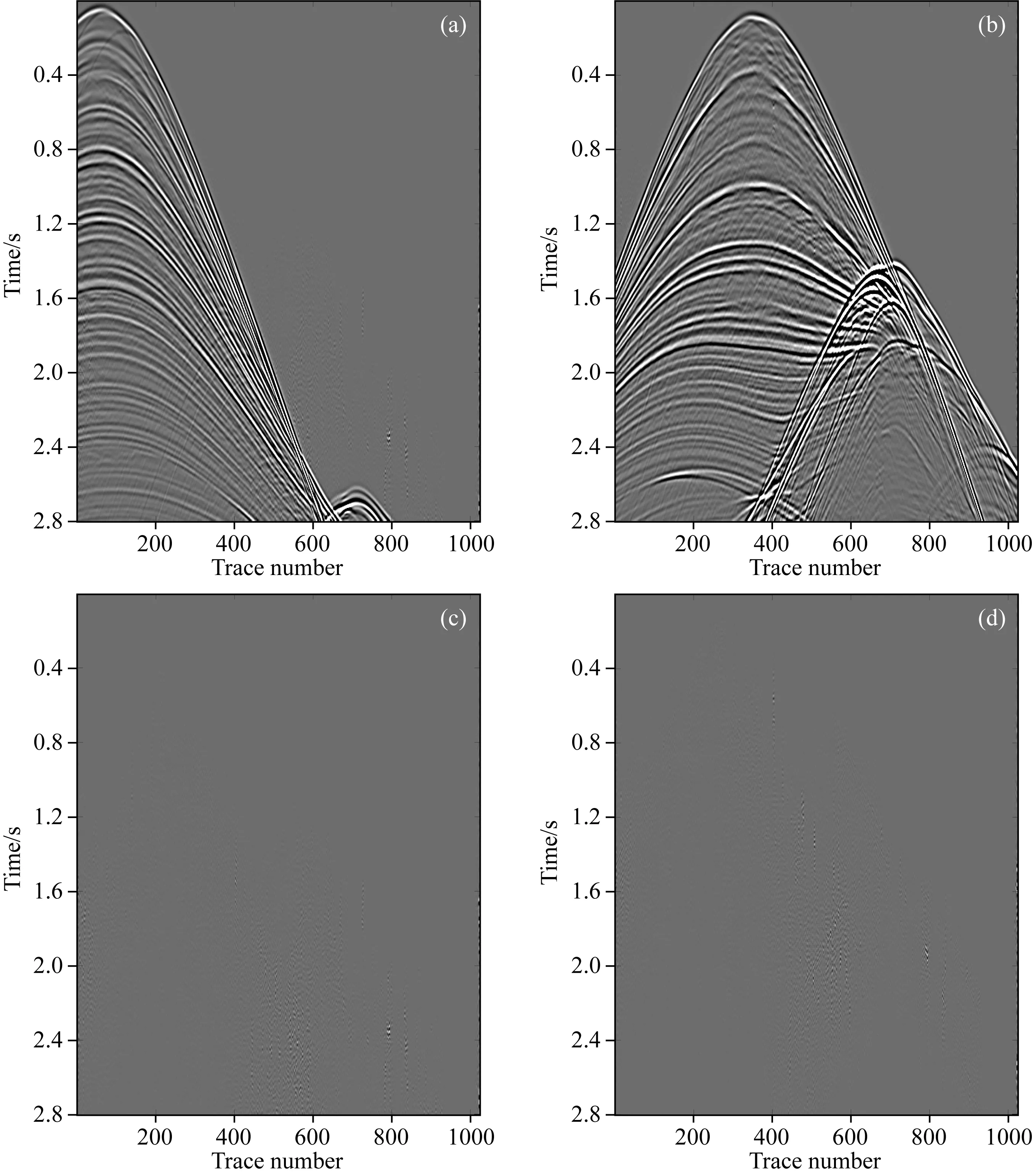
图11 本文提出的自适应阈值法分离结果和残差 (a) 主炮分离结果; (b) 干扰炮分离结果; (c) 图10a与图11a之间残差; (d) 图10b与图11b之间残差.Fig.11 Deblended results and the corresponding residuals from the proposed adaptive threshold method (a) Deblended result of the main source; (b) Deblended result of the interference source; (c) Residual betweenFig.10a andFig.11a; (d) Residual betweenFig.10b andFig.11b.
在相同的迭代反演框架下,分别用子带一致阈值法、Curvelet域指数衰减阈值法(祖绍环等,2016)和本文提出的自适应阈值法分离图2c中的混叠数据,证明自适应阈值法的优越性.图5a—c为主炮的分离结果,图6a—c为干扰炮的分离结果.从分离结果可以看出,这三种方法都取得了较好的分离效果,但是自适应阈值法能够保护有效信号特别是深部弱信号,残留噪声更少.为了更好地比较这三种方法的分离效果,分别将图2a与图5a—c数据相减、将图2b与图6a—c数据相减得到残差,然后将残差放大10倍后得到如图5d—f、图6d—f的放大后残差图.从残差图可以看出,子带一致阈值法没能很好地压制串扰噪声,同时也造成了有效信号的泄漏,残差大,分离结果较差;Curvelet域指数衰减阈值法对深部弱信号保留较好,但是串扰噪声强的部位不能够被很好地压制;本文提出的自适应阈值法能够有效的压制串扰噪声,更好地恢复和保护深层弱信号,分离结果好,残差小.为了更加细致的对比分离效果,我们分别提取原始主炮数据(图2a)、混叠数据(图2c)和分离结果(图5a—c)中第110和300道的数据,绘制如图7所示的单道波形对比图.从单道波形对比图中可以发现,这三种方法都能去除混叠数据中的噪声,分离的结果都与原始未混叠数据接近,但从图中放大部位可以看出本文自适应阈值法分离得到的数据与原始主炮数据更相近.图8为从残差图5d—f中抽取的第110和300道数据,反映了分离误差的大小,能够进一步展示图7中的三种方法分离得到的结果与原始主炮数据的接近程度.图8中的数值越小,证明分离结果与原始主炮数据越接近,分离效果越好.可以看出,自适应阈值法分离得到的误差比子带一致阈值法和Curvelet域指数衰减阈值方法分离得到的误差小很多,在4s以后的弱信号部位,自适应阈值法得到的分离误差几乎为0,由此证明了本文自适应阈值法具有良好地保护弱信号的能力.
为了定量分析分离效果,我们定义如下信噪比公式:
(14)
2.2 SEAM模型数据
SEAM模型包含倾斜地层、盐丘等复杂地质构造,是工业界常用的另一个测试模型.图10a和图10b分别为主炮和干扰炮激发采集的未混叠的共检波点道集数据,共1024道,可以看到盐丘产生的反射层信号能量很强.在0~1 s随机延迟时间作用下,干扰炮波场会以伪随机噪声的形式叠加到主炮波场中,混叠度m=2,形成如图10c的混叠波场.本次测试的分离方法是本文提出的自适应阈值法,加速因子λ2中α为0.7,其他测试条件与前文相同.图11a为主炮分离结果,收敛后的信噪比为27.88 dB,图11b为干扰炮分离的结果,收敛后的信噪比为31.31 dB,可以看出,使用自适应阈值法分离SEAM模型的同时震源数据同样具有较高信噪比,有效信号几乎被完全恢复,位于盐丘内部的弱反射信号得到了很好的保留,同样证明了自适应阈值法能够很好地保护弱信号,具有良好的分离效果;图11c为图10a与图11a之间的残差,图11d为图10b与图11b之间的残差,可以看出,除了反射波能量过大的部位残留少量噪声外,大部分串扰噪声得到了很好地压制,残差较小.图12为分离得到的信噪比曲线,通过40次迭代实现收敛,用时93.2 s,效率高.
2.3 第一个实际数据
使用Petroleum Geo-Services(PGS)公司公开的海上实际数据测试本文提出的自适应阈值法的分离效果.为了获得更加复杂的同时震源数据,我们截取原数据进行了人为混叠.实际数据的炮数和检波点数都是256,采样间隔为4 ms,混叠度m=2,加速因子λ2中α为0.7,其他条件与前文相同.图13a为原始主炮数据;图13b为原始干扰炮数据;原始干扰炮数据在2 s内的延迟时间编码下与原始主炮数据混叠得到混叠数据,如图13c所示.可以看出,在原始主炮数据与原始干扰炮数据中,浅部信号的能量都很强,远大于深部弱信号.
使用自适应阈值法分离图13c中的混叠数据.图14a为主炮分离结果,收敛后的信噪比为23.37 dB,图14b为干扰炮分离的结果,收敛后的信噪比为21.27 dB,图14c为图13a与图14a之间的残差,图14d为图13b与图14b之间的残差.图15为分离的信噪比曲线.自适应阈值法取得了较高的分离信噪比,能很好地压制串扰噪声,保护深层弱信号,由残差数据(图14c—d)可见深部几乎没有有效信号泄漏,本次测试在第37次迭代时实现了收敛,用时89.2 s,证明了本文自适应阈值法对实际的同时震源数据同样具有优越的分离效果和高效的分离速度.
2.4 第二个实际数据
使用某工区实际采集的同时震源地震数据进一步验证自适应阈值法的有效性.检波点间距和炮点间距均为25 m,每道共1020个采样点,采样间隔为4 ms,混叠度m=2.在本次测试中,加速因子λ2中α为0.7,其他测试条件与前文相同.图16a为混叠的共偏移距道集,串扰噪声散布在整个道集中,深部弱有效信号被湮没.使用本文提出的自适应阈值法得到的主炮和干扰炮的分离结果分别如图16b和图16c所示.从分离结果可见浅部强反射同相轴连续性更好,深部弱反射同相轴清晰可见,强噪声被完全压制,剖面的信噪比显著提高.本次测试进一步证明了自适应阈值法的有效性.
3 讨论
在自适应阈值法中,衰减系数α能够促进和加快迭代的收敛,我们同样使用Marmousi模型数据讨论α对分离效果的影响.当α的取值分别为0.2,0.3,0.4,0.5,0.6,0.7,0.8和0.9时,使用自适应阈值法分离图2c中的混叠数据得到如图18所示的主炮分离信噪比曲线.在图18中,随着α的减小,收敛需要的迭代次数减少,收敛速度明显加快,但是当α小于0.6时,收敛后的信噪比也出现了明显的下降;当α取值在0.7~0.9之间时,收敛后的信噪比一致且较高;当α为0.9时,收敛后信噪比较高,但是收敛需要的迭代次数明显多于α为0.8时收敛需要的迭代次数.通过讨论可以发现,α越小,收敛速度越快,但是过小的α会影响分离效果,所以我们需要在分离效果和收敛速度之间做出一个平衡,而α取值为0.6~0.8是一个较为合理的选择.
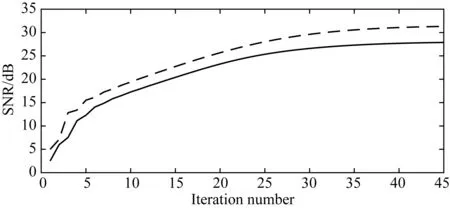
图12 本文提出的自适应阈值法分离 SEAM模型数据的信噪比曲线 其中实线代表主炮的分离信噪比,虚线代表干扰炮的分离信噪比.Fig.12 The SNR with respective to the iteration number for SEAM model data using the proposed adaptive threshold method The solid line is for the separated SNR of the main source, and the dashed line for the separated SNR of the interference source.
4 结论
在同时震源数据的迭代反演分离过程中,待处理地震数据经过Contourlet变换后,有效信号和串扰噪声在不同尺度和不同方向的子带中具有不同的分布规律,因此使用子带一致Wiener阈值方法往往得不到好的分离结果.在稀疏域迭代反演框架下,本文提出了一种在Contourlet域分离同时震源数据的自适应Wiener阈值方法.在迭代初期,自适应Wiener阈值方法中的噪声方差计算具有尺度自适应能力,能够适当增大高频子带中的噪声方差估计量,相比于使用全局一致的噪声方差计算方法,更利于达到快速压制串扰噪声的目的.在迭代后期,地震数据中的有效信号在稀疏域中多表现为数值较大的能量聚集点,自适应Wiener阈值方法使用局部加窗法计算有效信号方差,比子带一致的有效信号方差能更加准确地反映实际方差的大小,能够避免因为有效信号方差计算偏小而导致弱信号泄露.实验结果证明,本文Contourlet域自适应Wiener阈值方法能够快速有效地压制串扰噪声和保护有效信号,取得了比Contourlet域子带一致Wiener阈值方法和Curvelet域指数衰减阈值方法更好的分离效果.
在估计噪声方差时,本文自适应Wiener阈值方法只考虑了噪声数据在Contourlet域中不同尺度下的分布规律,如何将同一尺度下的不同方向特征也考虑进去需要进一步研究.

图13 第一个实际数据 (a) 原始主炮数据; (b) 原始干扰炮数据; (c) 混叠数据.Fig.13 The first field data (a) Original data of the main source; (b) Original data of the interference source; (c) Blended data.
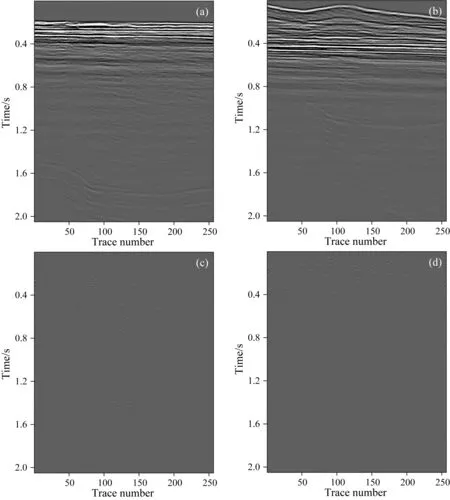
图14 本文提出的自适应阈值法分离第一个实际数据的分离结果和残差 (a) 主炮分离结果; (b) 干扰炮分离结果; (c) 图13a与图14a之间残差; (d) 图13b与图14b之间残差.Fig.14 Deblended results of the first field data from the proposed adaptive threshold method, and the corresponding residuals (a) Deblended result of the main source; (b) Deblended result of the interference source; (c) Residuals betweenFig.13a andFig.14a; (d) Residuals betweenFig.13b andFig.14b.
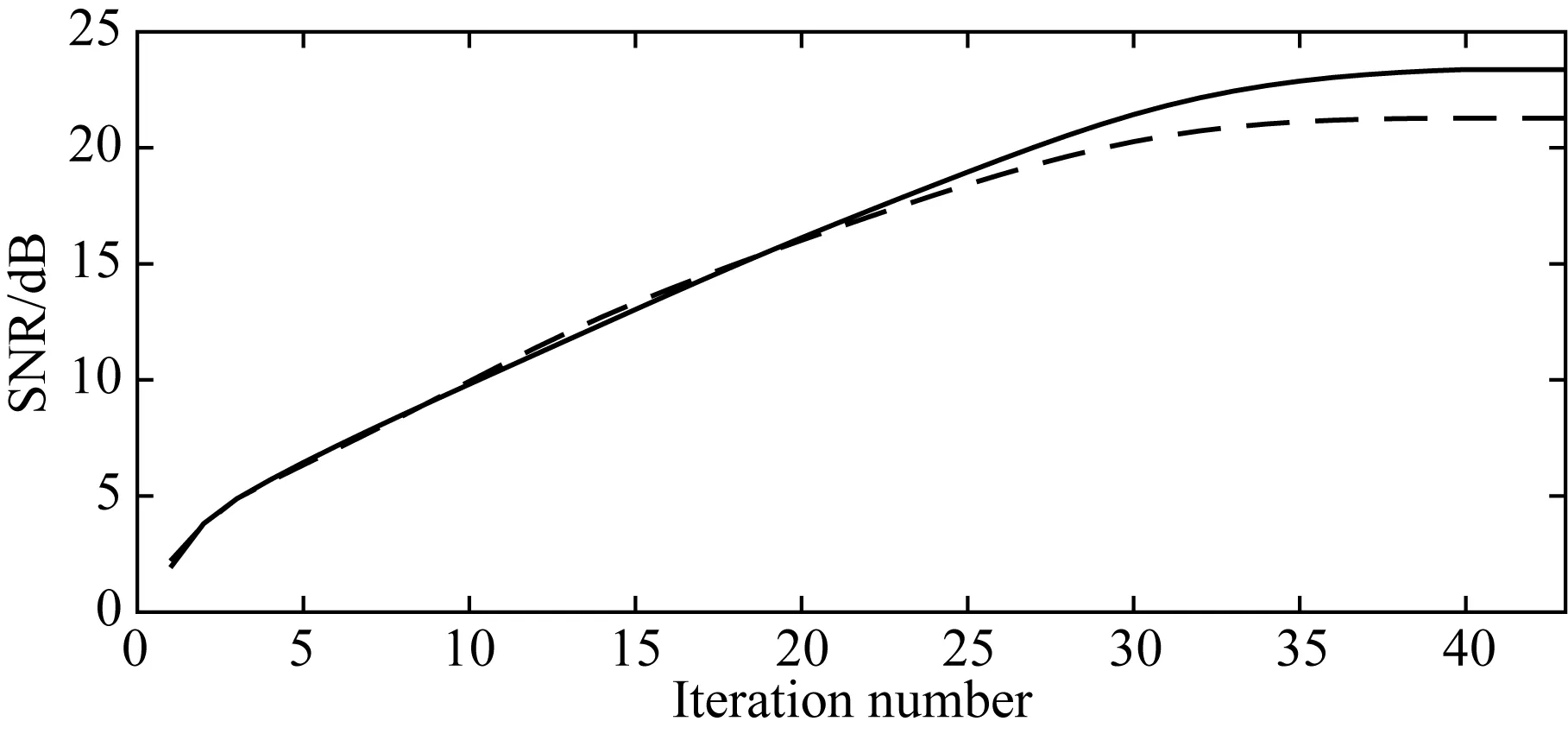
图15 本文提出的自适应阈值法分离 第一个实际数据的信噪比曲线 其中实线代表主炮的分离信噪比,虚线代表干扰炮的分离信噪比.Fig.15 The SNR with respective to the iteration number for the first field data using the proposed adaptive threshold method The solid line is for the SNR of the main source, and the dashed line for the SNR of the interference source.
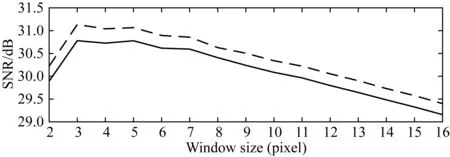
图17 不同窗口长度w对本文自适应阈值法 分离效果的影响 其中实线代表主炮的分离信噪比,虚线代表干扰炮的分离信噪比.Fig.17 The effect of different window sizes w on the separation effect from the proposed adaptive threshold method The solid line is for the SNR of the main source, and the dashed line for the SNR of the interference source.

图16 第二个实际数据的分离测试 (a) 混叠数据; (b) 主炮分离结果; (c) 干扰炮分离结果.Fig.16 The deblending test of the second field data (a) Blended data; (b) Deblended result of the main source; (c) Deblended result of the interference source.
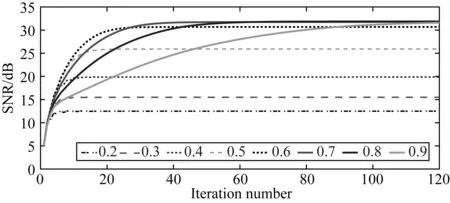
图18 衰减系数α取不同值时,本文自适应阈值法 得到的主炮分离信噪比曲线Fig.18 The SNR curves during the separation of the main source from the proposed adaptive threshold method by taking different values of attenuation parameter α

