基于主体企业的供应链创新模式比较与协调

宋志兰，王 融

（云南财经大学 物流学院，云南 昆明 650221）

0 引言

随着经济全球化的进程加快，几乎所有行业的公司或多或少地都选择了进行合作，以实现之前由单个企业无法达成的目标。在供应链结构日趋复杂的今天，更多类型的供应链企业之间的协作和创新出现在视野中，并且随着产品的生命周期越发短暂，市场的不确定性大幅度增加，企业面临的挑战愈发困难与复杂，其中竞争优势的维护便是一大难题。与此同时，供应链企业间创新协作的相关理论发展迅速，对现实问题同样具有指导意义，以实现企业降低产品创新风险和实现利润扩大的目的。

在这些创新协作的模式中，参与者包括在供应链中拥有着紧密供求关系和部分竞争关系的上下游的供应商企业和制造商企业，也存在着独立于供应链存在的提供某些服务的第三方研究机构。

有关供应链创新协作方面的文献从供应链结构、组织行为、协作契约等方面进行了研究与分析。梁喜，等[1]对由制造商与零售商所组成的双渠道供应链的创新问题进行了研究，其中，政府进行双重补贴不仅提高创新水平，且对供应链各方均有益。田巍[2]研究了单个供应商和单个制造商所构成的以制造商为核心企业的供应链的协作创新问题，发现供应链上下游紧密协作更有利于创新和各方利润提高。本文在其基础上对供应链结构进行扩展，引入多个供应商。肖美丹，等[3]研究了影响供应链中的创新活动的影响因素，发现激励系数对于其的相关关系。张菲菲，等[4]研究了基于领先客户的供应链协调模型，利用Stackelberg博弈的方法进行求解，研究说明了使得制造商利润最大的最优创新补贴的存在。马修岩，等[5]研究了对于创新型产品的两阶段供应链的协调问题，其存在批发价格契约策略使得供应链达到协调。张红，等[6]研究了考虑期权契约存在的供应链协调问题，发现引入创新成本共担机制可有效实现供应链协调和帕累托改进。杜衡[7]使用了报童模型分析随机需求下的供应链协调策略，其发现在成本分担的基础上引入余货补偿可以用来协调供应链。

在对国外文献的研究中，Gilbert，等[8]研究了供应链中的溢出效应及其影响，该效应及机会主义行为会使得创新投入减少，从而使得创新水平下降。Yang，等[9]研究了当制造商建立在线渠道进行销售所造成供应链冲突时，供应链转变为双渠道供应链可缓解冲突，并且提高运作效率。Qiao，等[10]总结了关于供应链的协作技术的创新，指出对供应链而言，协作创新仍是目前的研究热点及方向。Xu，等[11]研究了分散和集中条件下不同风险的供应链协调模型，结果表明集中比分散条件的创新水平高，风险规避水平越高，则批发价格越高。Nouri，等[12]研究了两阶段供应链，同时考虑制造商进行创新和零售商进行促销，通过补偿的批发价格合同对供应链进行优化。Zou[13]引入了信息化的背景，以创新供应链协调的新模式。Li，等[14]研究了政府补贴方案对于供应链创新的问题。Liu，等[15]指出智能供应链创新是企业提升其竞争力的关键所在。Zhu，等[16]采用鲁宾斯坦讨价还价博弈方法对制造商和供应商绿色创新努力对产品绿色水平的作用进行了分析。Wei，等[17]构建了政府和企业间的互动机制，考虑了政府对供应链创新的相关影响。Fu，等[18]以外部股权融资支持的第三方物流公司的技术创新为重点，得出其供应链效率取决于参与各方的成本分配。Shen，等[19]研究了供应链共同开发含有多个创新要素的产品，结果表明制造商主导的创新活动具有高价值，说明在供应链中，由制造商担任主体企业是更优的策略。

综上所述，本文对供应链的协作创新进行研究，以制造商为主体企业，考虑需求对价格敏感的情况下，分析了由两家供应商、制造商和第三方研究机构组成的供应链利用博弈进行创新协作的6种模式，对其进行建模与分析，并在此基础上引入算例进行数据统计与比较，得出有利于企业进行决策性行为的一般性结论。

1 问题描述

1.1 供应链结构

本文主要研究制造商作为供应链的主体企业与供应链上游的多个供应商企业所组成的两级供应链。为便于分析，假设上游供应链企业的数量为2，如图1所示，目的是要降低供应链的成本。假设制造商生产一个产品所需的零件可由两个供应商进行供应，且制造商选择供应商的原则为价低者得，即供应商1所提供的批发价为w1，供应商2所提供的批发价为w2，如果w1＞w2，则选用批发价格更低的供应商2作为合作企业；同理，若w1＜w2，则选用供应商1作为合作伙伴；当w1=w2时，则可以两家供应商同时进行原材料的供应。对于供应商而言，因为在供应链中处于上游位置，对制造商企业所需的零配件了解较深，且能够较好地识别制造商的需求，并且拥有对零部件所需配套设备和软件等关乎产品质量的研发能力，即可以达到降低生产和物流成本的目的，具有能够与制造商进行协作创新的能力。另外，假设在该市场中同样存在一类第三方研究机构，该机构同样能够进行创新活动，以达到降低成本的目的。

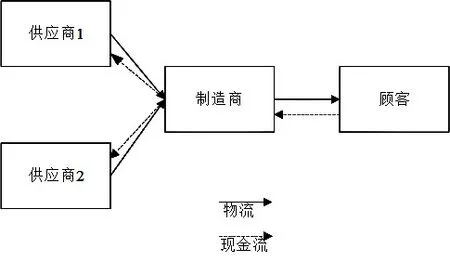
图1 供应链结构

1.2 模型表述

假设本文所建模型的环境具有信息通畅的条件，即对供应链各方来说信息具有完全对称的特征，不存在信息不对称。对制造商和各供应商而言，对待风险的态度均为中立。在模型中，降低成本可表现为使自身利润最大化。CS1、CS2和CM分别表示供应商1、供应商2和制造商的单位可变成本；对于核心企业制造商而言，其需求函数可表示为：D( p)=φ-βp，β＞0 ；w1、w2为制造商对于供应商1、2所提供的零件1、2的批发价格。p为制造商将产品销售给顾客的零售价格；φ 为制造商可能面临的最大需求量，φ＞0；β 表示制造商面临的需求对于p的敏感程度，也称D对p的敏感系数。为了使得研究有意义，令φ＞β( )

CS1+CS2+CM。本文通过建立不同模式的模型对以制造商为主体企业的供应链创新模式进行比较与分析，其中，不同模式都具有共性特征：供应链各方均可以进行创新及协作创新，而进行创新活动可以使得制造商生产产品的单位可变成本CM降低。假设对于创新活动的投资表示为v(θ)，通过数量为v(θ)的投资将其里假设w1＜w2；（2）制造商独自完成创新活动，且w1=w2；（3）制造商支持供应商进行协作创新且由某一指定供应商进行创新活动，此时w1≠w2，这里假设w1＜w2；（4）制造商支持供应商进行协作创新且由两供应商以1:1的比例进行创新，此时w1=w2；（5）制造商委托第三方机构进行协作创新，此时w1≠w2，这里假设w1＜w2；（6）制造商委托第三方机构进行协作创新，此时w1=w2。特别说明，本文使用πij分别表示各方利润，上标i=1，2，3，4，5，6表示协作创新模式，下标j=S1，S2，M，3P 分别表示供应商1，2及制造商和第三方研发机构。

2 解决方案

2.1 制造商独自完成创新活动，且w1 ≠w2

单位可变成本降低的期望值为θ，θ＜r ，其中0＜θ＜1，r 是创新投入的单位成本可减少的最大值。在本文中，令v(θ)=Iθ2，I为创新成本系数，且对于

在此模式中，供应链中的主体企业为制造商企业，并且制造商选择独自完成创新活动，以达到降低成本、提高利润的目的，并且进行三阶段的斯塔克伯格博弈，其具体表述为：（1）制造商制定本身的创新力度θ；（2）供应商制定向制造商出售原材料的w1、w2；（3）制造商制定销售价格p。这里假设w1＜w2。

阶段1：由以上分析可知θ和w1、w2，对于制造商而言，其利润表达式为：

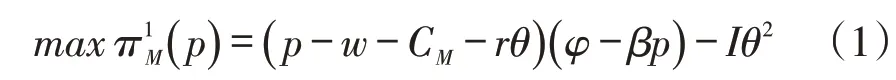
其中w=min[w1,w2]（在以下表述中，均为此表达）。研发投资而言，其特征为对于θ边际收益递减。I越小且r越大，就表明运作效率越高，创新投资就越大。注意：对于制造商而言，制造商会拥有一部分的固定成本无法通过创新投入而降低，即可表示为：r＜CS1,CS2。另外，假设4I＞βr2，以实现一般性的目的。

本文采用博弈方法对供应链创新协作的集中模式进行归纳，并分析创新活动对于核心企业和供应链各方企业的影响，进而比较得出其利润表达式。如图2所示，模式为：（1）制造商独自完成创新活动，且w1≠w2，这

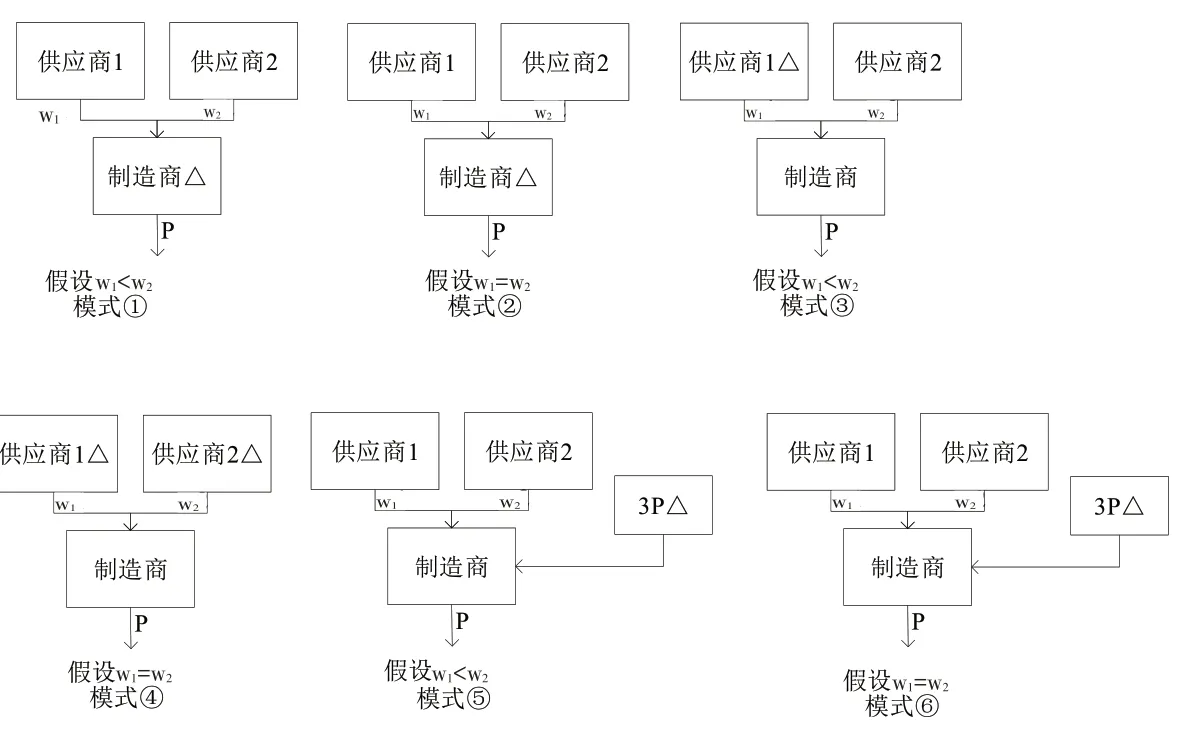
图2 供应链创新协作的6种模式

对于式（1）而言，其对p 的二阶导数=-2β ＜0 ，π1

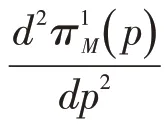
M(p) 为凹函数。若求其最大值，可令式（1）对p求一阶导数，并令其为0，可得制造商利润关于p的反应函数：

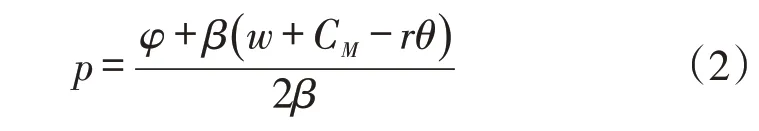
阶段2：因为两家供应商供应的原料是相同的，对于制造商而言，哪家供应商所提供的批发价格更低，则供应商就会选择该供应商进行合作。这里假设w1＜w2，即供应商1 的批发价格更低，则制造商的订单供应商1，即供应商1拥有全部订单，而供应商2在此情况中被淘汰，即不再拥有订单。在这里只讨论w1＜w2的情况，对于w1＞w2，只是订单接受者从供应商1 变为供应商2，即供应商2 拥有全部利润，CS1=CS2，其余与此处假设相同。此处假设为：

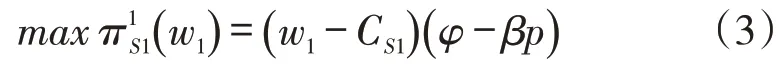
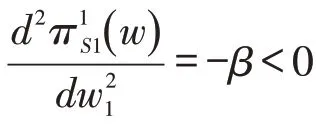
将式（2）代入式（3），同时式（3）对w1求二阶导数，即，可知对上游供应商1 而言，其利润表达式是关于w1的凹函数。对式（3）求关于w1的一阶导数并令其为0，可得供应商1 对应的反应函数：

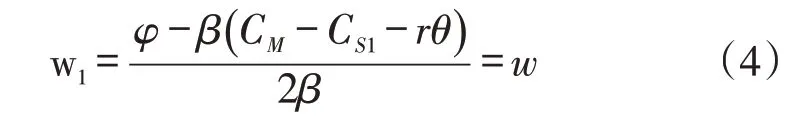
阶段3：将式（4）所代表的w 和式（2）所表达的p代入式（1）中进行整理，可得到关于θ 的表达式，此时，对该式求θ的一阶导数，可得令制造商利润最大的θ为：

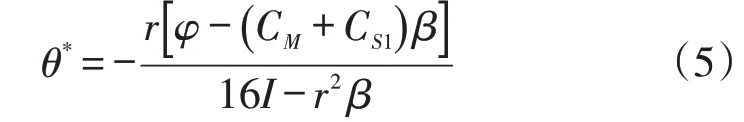
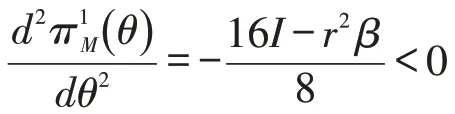
将式（4）、式（5）分别代入式（1）—式（3），可得该假设下所能达到的利润最大化的，同时，，其结果见表1。

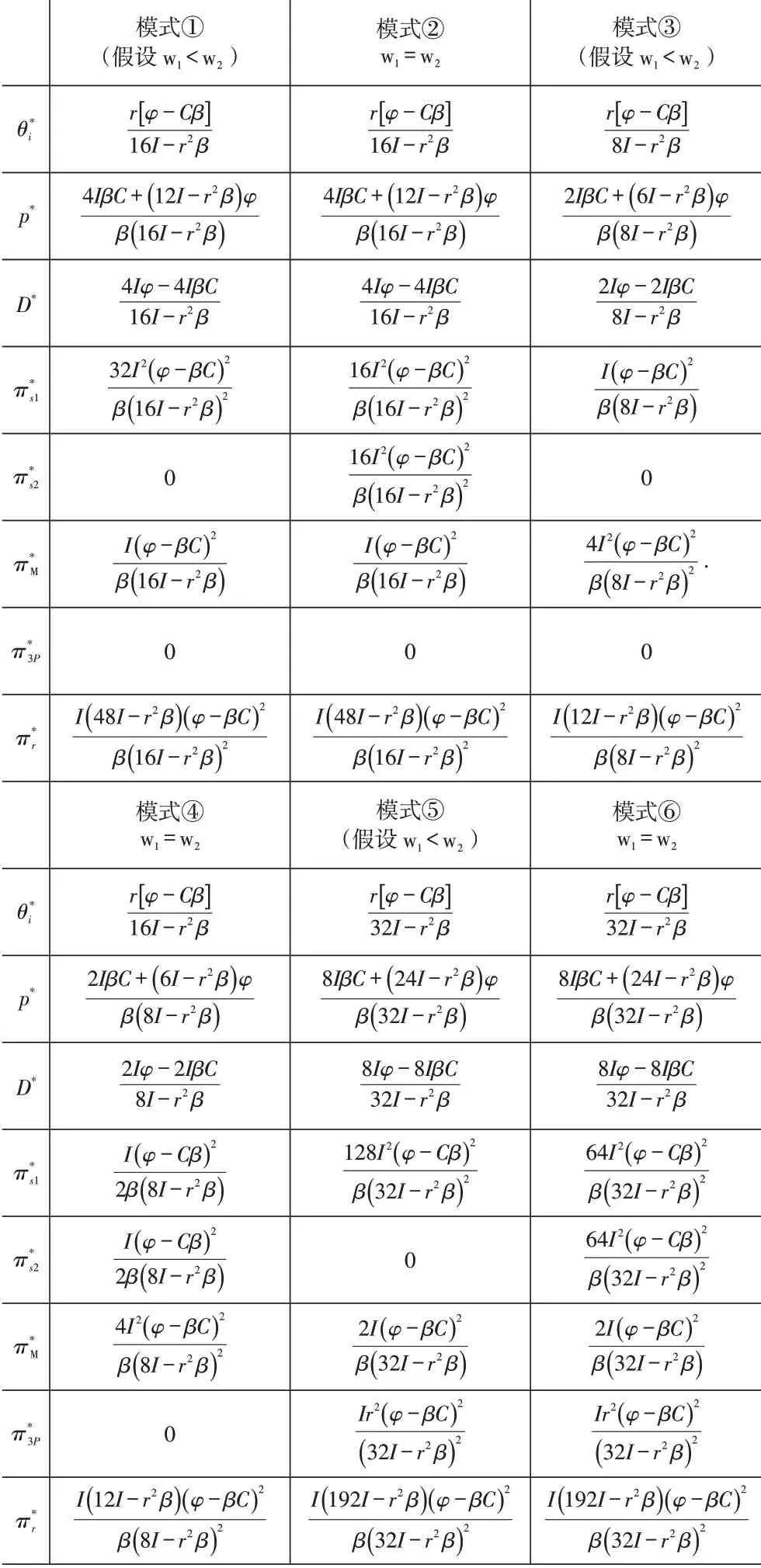
表1 供应链协作创新模式的结果

其中：（1）C=CS1+CS2+CM；（2）π*r表示整个供应链的整体期望利润的加总。

2.2 制造商独自完成创新活动，且w1=w2

在此模式中，供应链中的主体企业为制造商企业，并且制造商选择独自完成创新活动以达到降低成本、提高利润的目的，并且进行三阶段的斯塔克伯格博弈，其具体表述为：（1）制造商制定本身的创新力度θ；（2）供应商制定向制造商出售原材料的w1、w2；（3）制造商制定销售价格p。这里假设w1=w2。

阶段1：仍与第一种情况相同，其中令w=w1=w2，其制造商利润表达式仍为式（1）。对于p而言表达式仍为式（2）。

阶段2：因为两家供应商所提供的批发价格相等，所以对于制造商而言，两家供应商以相同的价格提供同质的原材料，所以订单会均分给两个供应商。所以对于供应商而言，预料到制造商的反应函数后，其利润表达式为：

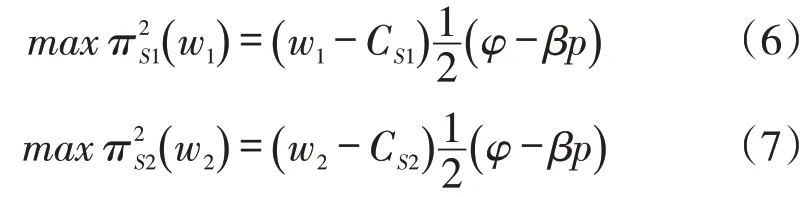
其中，CS1=CS2，对应分配到每个供应商的订单数为，也就是上文中单个供应商情况的50%。为方便计算，将以同价格且提供同质原材料的两家供应商视为一个大的供应商，将大供应商的利润 视 为，由 此 可 知，所以由此可知供应商的反应函数为：

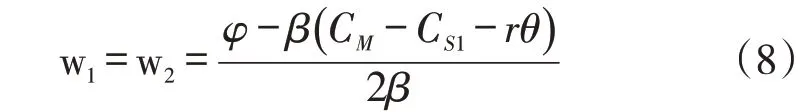
阶段3：将式（8）、式（2）代入到式（1）中，可得到制 造 商 关 于θ的 表 达 式。 此 时，对该式求θ的一阶导数，可得令制造商利润最大的θ为：

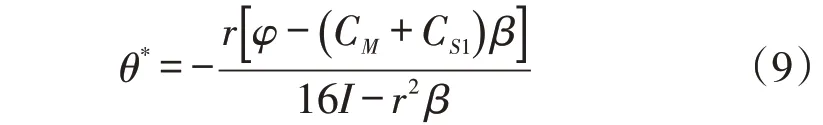
将式（8）、式（9）分别代入式（1）、式（2）、式（6）、式（7），可得该假设下所能达到的利润最大化的，同时，，且

因此，由制造商独自进行创新活动，且两个供应商以同价格提供同质产品的模式下，制造商的期望利润为：，相关结果见表1。

2.3 制造商对供应商进行协作创新支持且由某一指定供应商进行创新活动，w1 ≠w2

在此模式中，制造商可以通过支持上游供应商企业进行创新活动，以此来达到降低成本的目的。因制造商与供应商对信息获取能力的假设相同，所以制造商可以得知供应商进行创新的力度θi，如果被制造商选择进行创新协作，则其创新力度为θi，i代表供应商的序号，如果第i家供应商不被选择，则其θi=0。对于制造商而言，必然会选择批发价格更低的供应商进行合作，即选择更低批发价的供应商进行的补偿是补偿支付系数与创新力度的乘积。在该模式下，假定w1≠w2，即制造商会选择某一批发价格更低的供应商创新协作，由该供应商来进行创新的同时制造商对其进行创新的补偿支付，而不是两家供应商都进行创新活动。为方便计算，假设w1＜w2。此时居主体地位的企业仍为制造商，并进行阶段数为四阶段的斯塔克伯格博弈，其具体表述为：（1）制造商制定单位产品创新补偿的支付系数b，即单位产品支创新补偿为bθ，0＜b＜r ；（2）供应商制定自主的创新力度θ1,2以及对应的w1、w2；（3）制造商制定销售价格p。

阶段1：在已知b,θi,wi的前提下，制造商应对p进行制定，制造商的利润为：

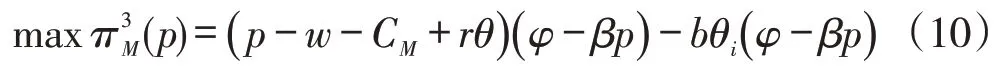
其中，w=min[w1,w2] 。式（10）为关于p 的凹函数，反应函数为：该式对p求一阶导数并令其为0，即：

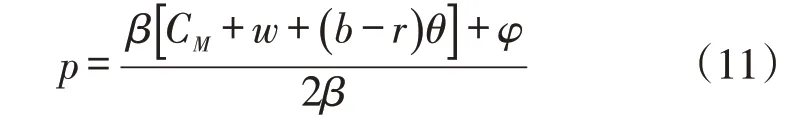
阶段2：供应商此时可对式（10）进行预测，则对供应商而言，供应商1所提供批发价小于供应商2，则此时供应商2 就不再参与博弈模型和创新活动。对于供应商1，其利润表达式为：

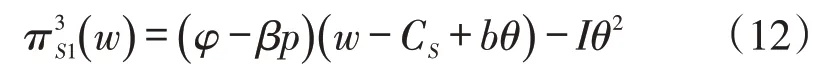
阶段3：将式（13）代入到式（12）中，则利润表达式关于θ的表达为：

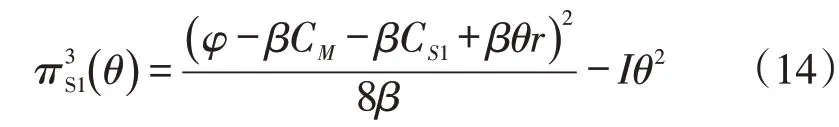
对式（14）求关于θ的二阶导数，，因此可由一阶导数为0得到θ的表达式为：

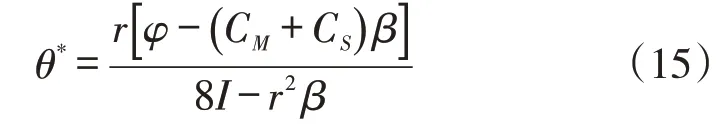
阶段4：将式（13）、式（15）、式（11）代入式（10），可得到制造商优化后的利润表达式和对应进行创新活动并获得全部订单的供应商1的利润表达式为：

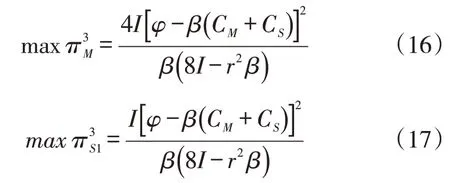
剩余结果见表1。

2.4 制造商支持供应商进行协作创新且由两供应商以1:1的比例进行创新，此时w1=w2

在此模式中，仍然是制造商对上游的供应商企业进行支持性的创新协作来降低成本，但与上一种模式的不同之处在于：本模式中两个供应商所提供的同质产品的批发价格相同，即w1=w2。对于制造商而言，其仍然会对供应商的创新协作支付补偿，且补偿表示为bθ0；对于供应商而言，其所提供发价格、产品质量、进行创新活动的力度均相同，即两个供应商同时进行同样程度的创新活动，所以对于单个供应商而言获得的补偿应为，且两个供应商获得的补偿相等。本模式四阶段的斯塔克伯格博弈流程为：（1）制造商依据上述规则制定创新补偿支付系数，并且其大小满足[0,r]；（2）供应商制定该企业进行创新的力度，即θ1,2，以及依据该创新力度而对应于制造商的批发价格w1、w2；（3）核心企业制造商制定其产品的售价p。

阶段1：在已知b,θi,wi的前提下，制造商应对p进行制定，制造商的利润为：

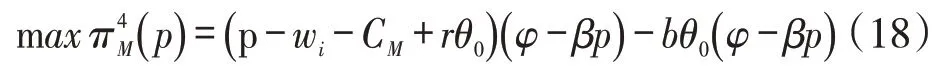
式（18）是关于p的凹函数，该式对p求一阶导数并令成0，得反应函数为：

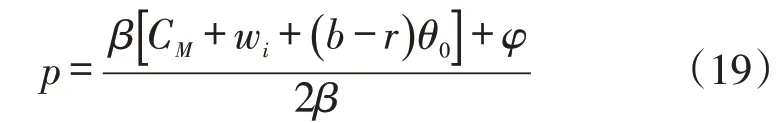
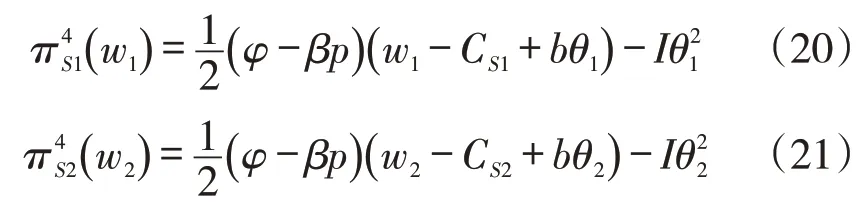
其中bθ0=bθ1+bθ2=b(θ1+θ2)。对式（20）求关于w1的二阶导数为，对于式（21）求关于w2的二阶导数为。根据一阶条件可知：

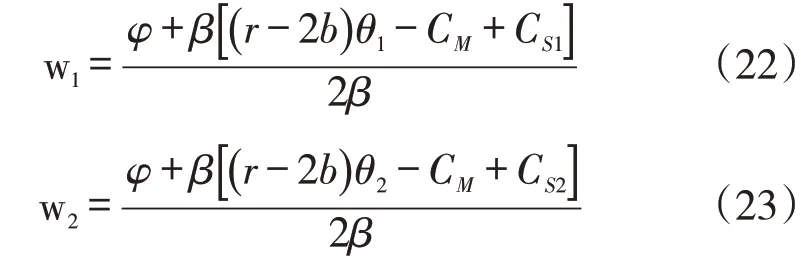
阶段3：式（22）、式（23）与式（19）分别代入式（20）与式（21），其利润关于θ1,2的表达式为：

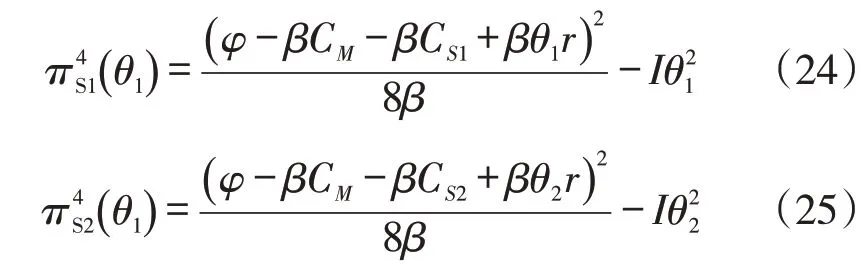
对于式（24），式（25）而言，w1=w2，θ1=θ2，CS1=CS2。对式（24）、式（25）求关于θ1,2的二阶导数可得，由此可知式（24）、式（25）为凹函数。对式（24）、式（25）分别求关于θ1、θ2的一阶导数并令其为0，可得：

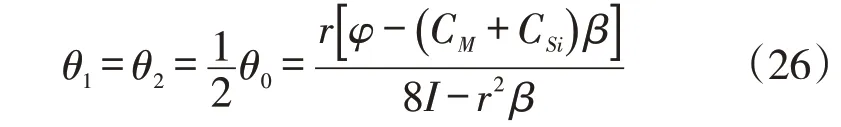
阶段4：将式（26）、式（22）、式（23）、式（19）代入式（18），可得到该模式下的主体企业制造商的期望利润为：

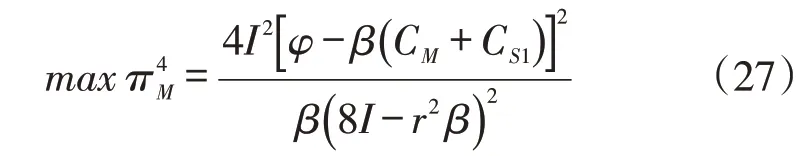
根据式（27）可知，制造商期望利润的最终表达式与一开始所设的补偿系数b 无关，但是式（22）、式（23）却表示b 与wi的关系呈反比关系，则该供应链可通过b与wi的调整来进行利润的重新分配。

其他结果见表1。

2.5 制造商委托第三方机构进行协作创新，且w1 ≠w2

在该种模式下，制造商本身与上游的供应商都不进行创新活动，由作为主体企业的制造商与第三方研究机构进行协作创新。在有第三方研究机构参与的一般商务模式中，委托人通常按照第三方研究机构所做出的创新度来进行薪酬计算，在本模式中，制造商需要向第三方研发机构支付tθ，其中t为本模式的创新补偿支付系数。本模式的斯塔格伯格博弈分四阶段进行，依次为：（1）由主体企业先宣布对第三方研究机构的支付补偿系数b，其中b∈[0,r]；（2）第三方研究机构根据委托方给出的支付系数确定θ；（3）上游供应商制定其批发价格w；（4）根据第三方的创新开发力度θ 和供应商所制定的w1、w2，主体企业制造商确定产品的售价p。这里假设w1＜w2。

阶段1：对主体企业制造商而言，其利润表达式如下：

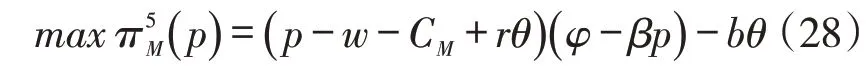
对于式（28）而言，w=min[w1,w2] ，式（28）表明制造商会选择向它提供更低批发价格的供应商来进行交易。其关于p 的二阶导数小于0，所以为凹函数。由其一阶导数为0可得制造商的反应函数为：

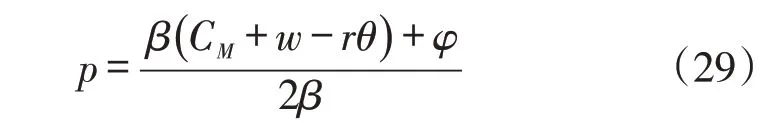
阶段2：供应商1、2 的批发价格分别为w1、w2，此时我们假设：w1＜w2，即制造商会倾向选择供应商1（当w1＞w2时，其对于供应商1、2 的利润交换，其他情况均相同）。对制造商的反应函数进行预测，供应商的利润可表示为：

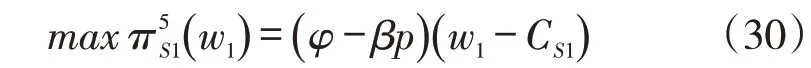
将式（29）代入式（30）后对w1求二阶导数，可知，故其式为凹函数，由其一阶导数为0可知：

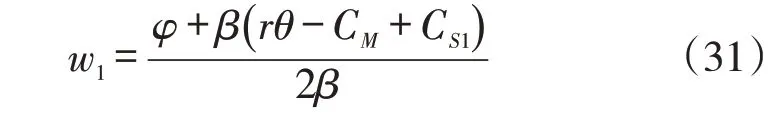
阶段3：对于本模式而言，引入了第三方研究机构与主体企业供应商进行创新协作，即第三方研究机构也算是本供应链的一部分。其表达式如下：

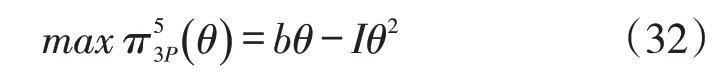
由式（32）对θ求一阶导数并令其为0，可得：

阶段4：将式（29）、式（31）、式（33）代入式（28），主体企业供应商的利润表达式为：

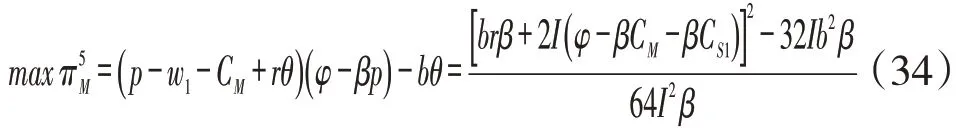
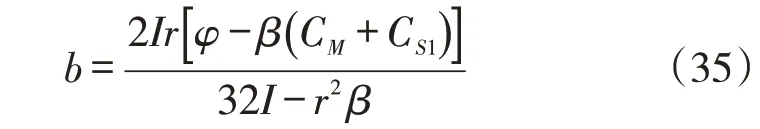
此模式的结果见表1。

2.6 制造商委托第三方机构进行协作创新，且w1=w2

在该种模式下，制造商本身与上游的供应商都不进行创新活动，由作为主体企业的制造商与第三方研究机构合作进行协作创新。在本模式中，制造商需要向第三方研究机构支付tθ，其中t为本模式的创新补偿支付系数。本模式的斯塔格伯格博弈分四阶段进行，依次为：（1）由主体企业先宣布对第三方研发机构的支付补偿系数b，其中b∈[0,r]；（2）第三方研究机构根据委托方给出的支付系数确定θ；（3）上游的供应商制定其批发价格w；（4）在得到第三方的创新开发力度θ 和供应商所制定的w1、w2后，主体企业制造商确定产品的售价p。这里讨论w1=w2的情况。

阶段1：对主体企业制造商而言，其利润表达式如下：

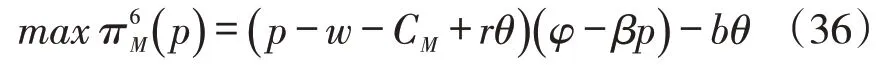
在本模式中，w=w1=w2。式（36）表示对于制造商而言，选择供应商1 和选择供应商2 的情况都相同，所以主体企业制造商会将订单均分给两个供应商，式（36）关于p的二阶导数小于0，即为凹函数。由其一阶导数为0可得制造商的反应函数为：

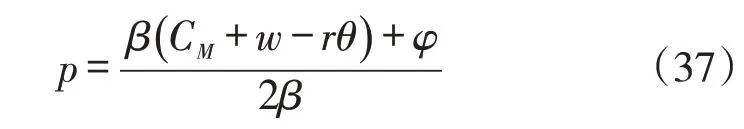
阶 段2：供 应 商1、2 的 价 格 为w1、w2，其 中w1=w2。由此可知主体企业制造商将会与两个供应商企业进行交易，此时供应商企业对制造商的反应函数进行预测，供应商1、2的利润表达式为：

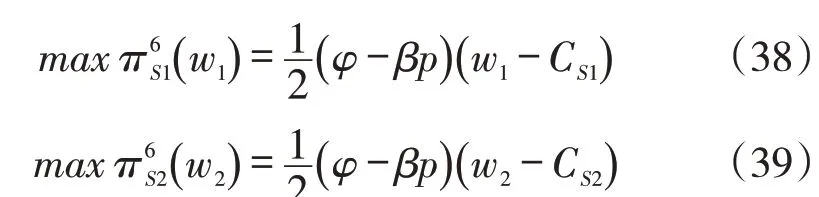
此时，CS=CS1=CS2，将式（37）分别代入式（38）与式（39），其关于wi的二阶导数为：，所以式（38）与式（39）为关于wi的凹函数，由其一阶导数为0可得：

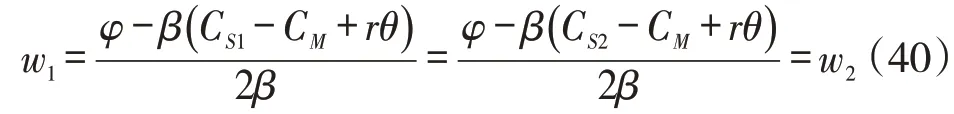
阶段3：在本模式中，第三方研究机构的利润表达式为：

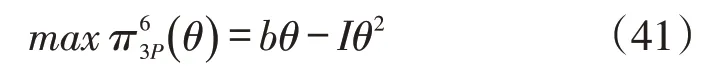
令式（41）对θ求一阶导数且等于0，得到：

阶段4：将式（37）、式（40）、式（42）代入式（36），则制造商利润表达式为：

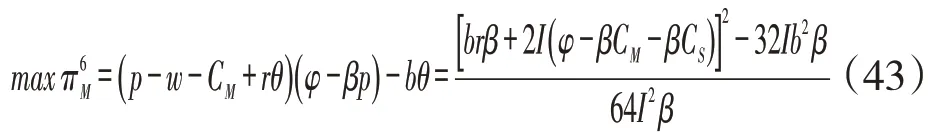
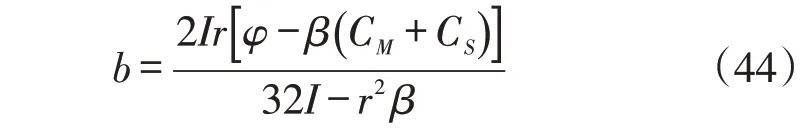
此模式其他结果见表1。

3 算例分析及比较

3.1 数据分析

为便于进一步研究，引入A公司数据对以上6种模型进行赋值，代入后进行分析与比较，从而得到对于主体企业制造商最有利的选择。

在这里我们假设供应商之间存在两种关系：其所提供的批发价格相等或不相等。在前面章节建立的数学模型的基础上，假设r=1,φ=5,C=CS1+CS2+CM=5,β=0.2,I=0.6，分别代入六种模型，可以得到表2。

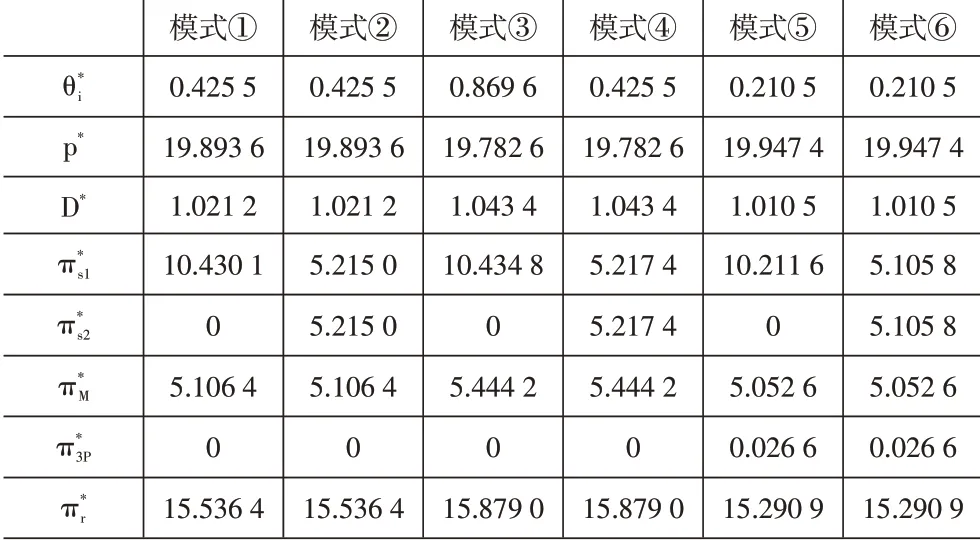
表2 代入算例的各决策变量及利润

对于表2，以图表形式分别表达，如图3-图10所示。

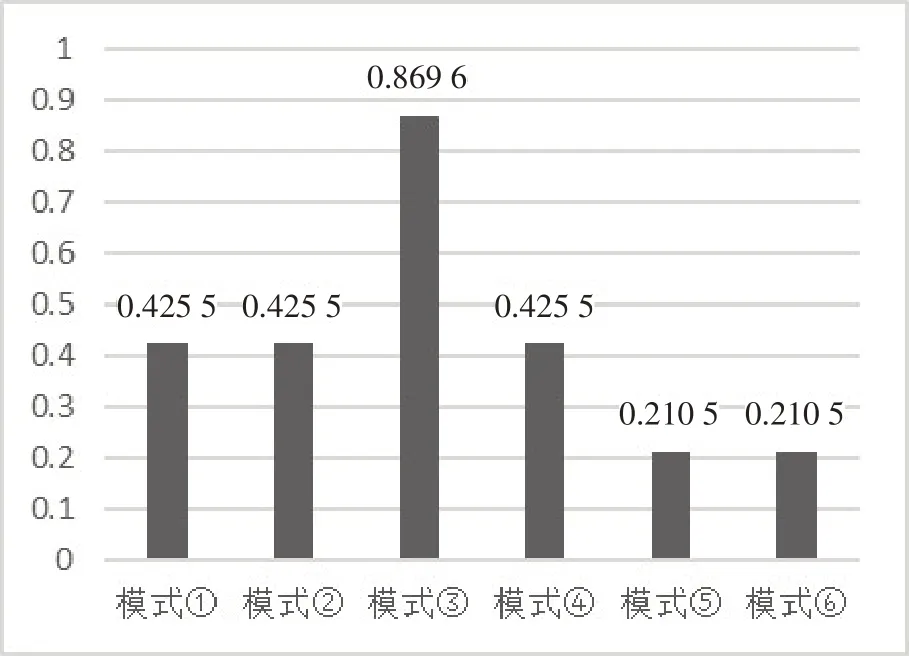
图3

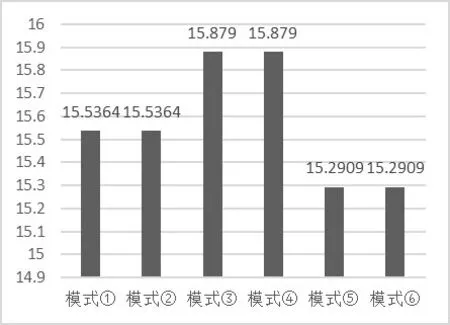
图10

3.2 模式比较

根据表2计算结果可得以下结论：

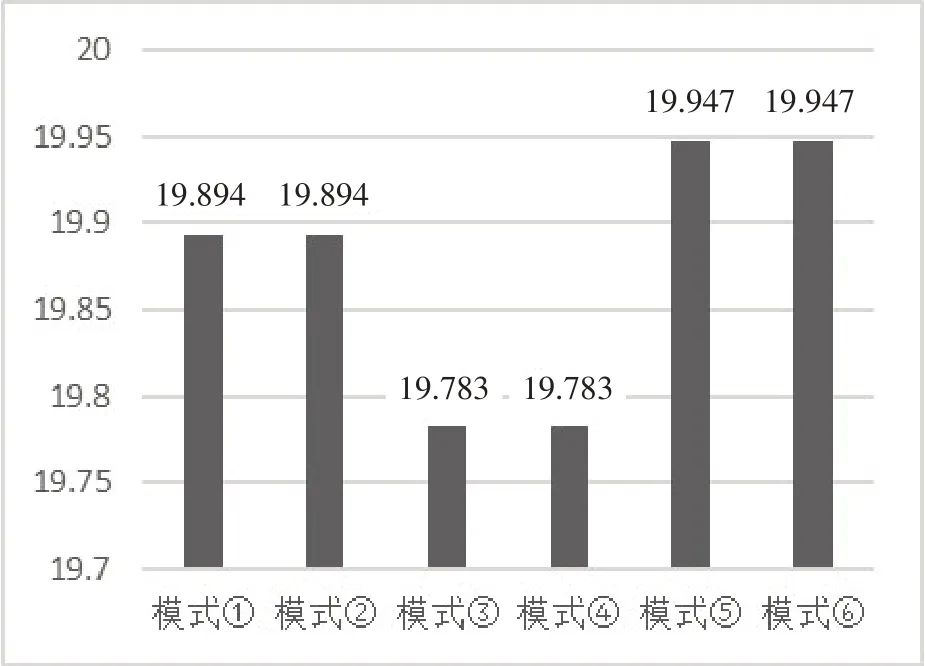
图4 p*

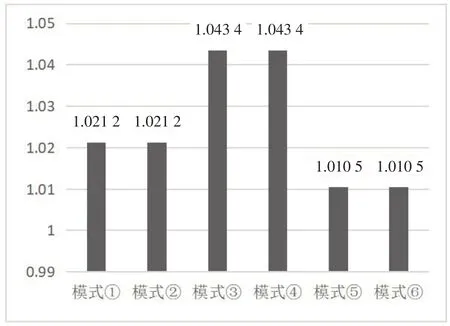
图5 D*

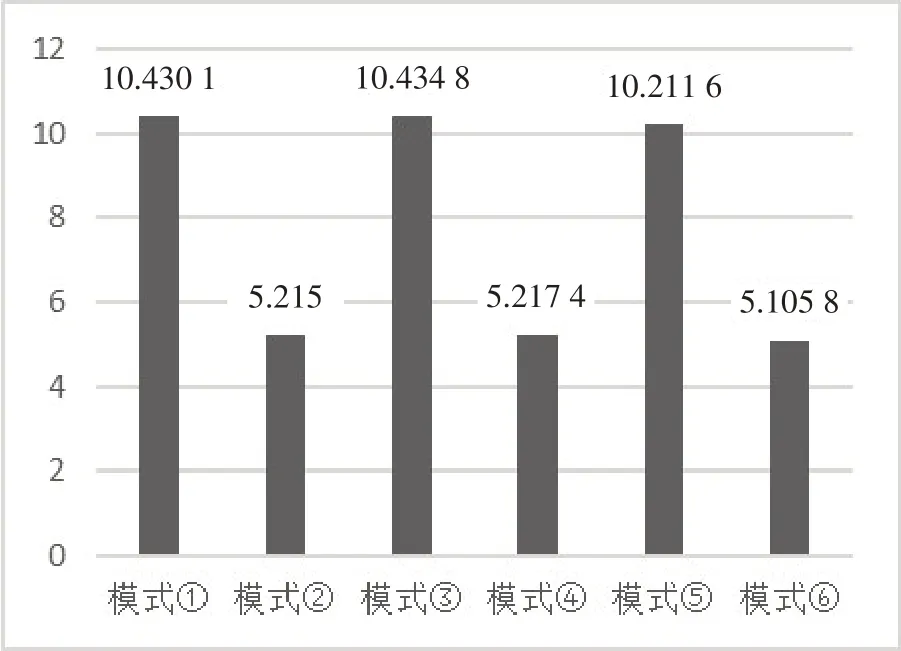
图6

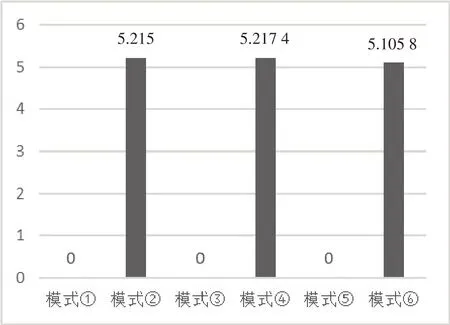
图7

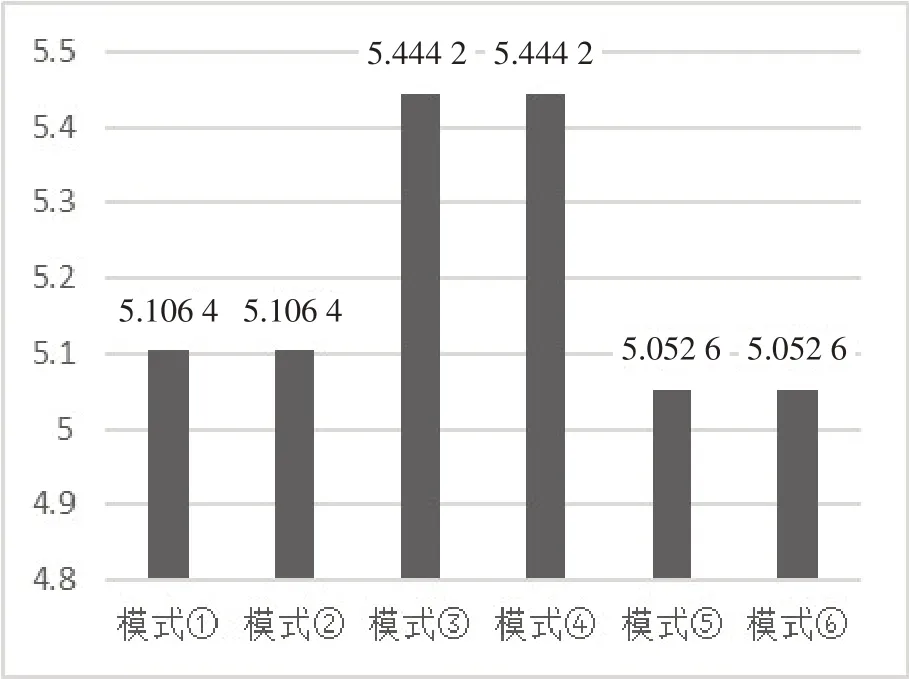
图8

结论1θ3*＞θ4*=θ1*=θ2*＞θ5*=θ6*。结论1说明对于供应商而言，模型①②⑤⑥在由其他方确定创新力度θ后，再确定其所提供的w，在双边际化的影响下，这种创新协作的方式会降低创新方的单位产品边际利润，因此创新方的积极性下降。模型③与④避免了前面所述问题，且因为存在两种供应商所提供批发价格的情况，对于单个供应商而言，由一个供应商进行创新活动会比两个供应商同时进行创新活动的创新力度更大；对于制造商而言，无论由几家供应商完成创新活动，主体企业所得到的利润和付出的创新成本均相同。

结论2p5*=p6*＞p1*=p2*＞p3*=p4*。结论2 说明制造商支持供应商进行创新会使得其自身的销售价格更小，而选择第三方研究机构进行创新则会使其销售价格更大。因为p是制造商面临的问题，不管是与单一供应商达成合作还是与两家供应商同时达成合作，对作为供应链中主体企业的制造商而言，其所带来的影响均相同，即对制造商而言的售价与两家供应商所提供原料的批发价格的关系如何无关。

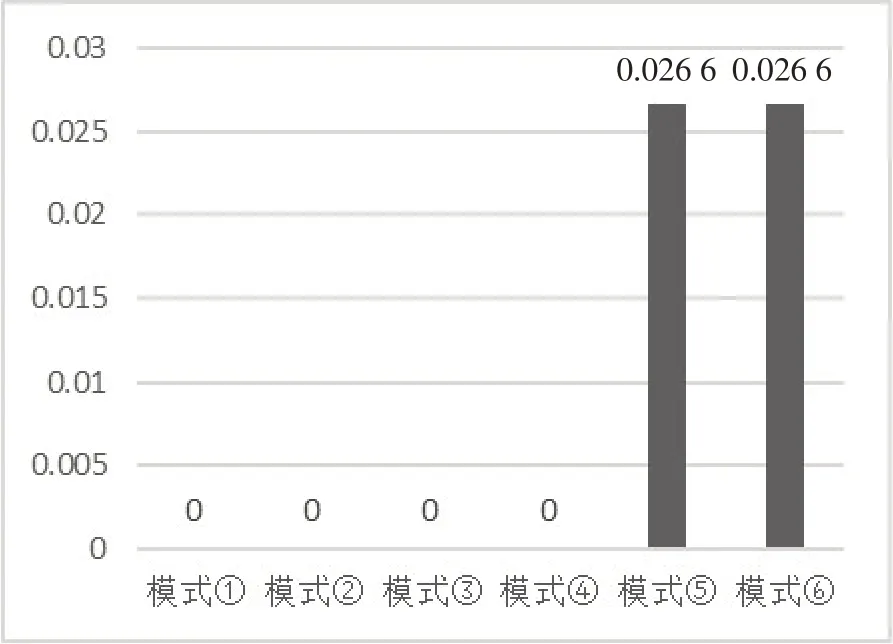
图9

结论3D3*=D4*＞D1*=D2*＞D5*=D6*。结论3中D 的含义为该商品的需求，在制造商对供应商进行创新支付补偿的模式下，其需求最大，意味着该类创新协作模式可以增加社会需求，提高社会购买能力，由于创新活动所创造的社会总福利也因此最大。

结论4.2 当w1≠w2时，，i 为提供更低批发价格的供应商的编号。

结论4.3 当w1=w2时，

结论4 由5 个利润的分析部分组成。对于主体企业制造商而言，与供应链上游的供应商进行创新协作可以提高利润，并且能够有效降低创新所伴随的风险，创新水平得到提高的同时，也能够提高上游企业的利润和供应链整体的竞争力。对于上游供应商企业而言，如果两家供应商进行竞争，即使两家所提供原料的批发价格相同，对于单个供应商的利润而言会比由一家供应商进行供应要少。对于供应商批发价格不相同的情况，等价于某一供应商因同质原料售价过高而退出该市场环境；对于两家供应商的批发价格相同的情况，等价于某一大供应商分裂成两个提供同质同价原料给同一供应链中的主体企业的小型供应商。但不论两家供应商所提供的批发价格大小关系如何，与制造商进行创新协作，即由主体企业制造商对供应商进行创新支付补偿，对供应商企业来说是利润最大化的选择，该选择同时也使得整体供应链最优。

4 结语

本文针对供应链中的主体企业制造商，假设需求对价格变化较为敏感，研究了供应链中的上游供应商、主体企业制造商和第三方研究机构之间的相互协作创新的博弈，从而使得各方利润最大化，其中主要研究了6 种创新模式，对其进行建模分析研究，并进行了对比和优化。

基于上文研究发现，在创新能力一定的情况下，对利润而言，供应链中的上游供应商与主体企业制造商的协作创新模式可以降低投资和创新风险，且提高了创新水平，不论对制造商还是供应商而言，利润相比没有进行创新协作时更大。本文在此基础上，对多个供应商（本文仅讨论存在两个供应商企业）的情形进行了6种不同模式的创新协作的建模分析，对比而言，制造商对供应商进行支持，紧密的协作方式更加有利于利润的最大化和供应链整体利润的提高。而在制造商支持供应商进行创新协作的前提下，与单个供应商进行交易和与两个供应商同时进行交易对主体企业制造商而言是完全相同的情况，对于某一供应商而言，存在与自身所提供批发价格相同的竞争者比由自己本身来完成全部的订单所获得的利润更少。

此外，本文是在信息对称的前提下进行上述研究，并且仅考虑了两个上游供应商的情况，具有一定的局限性。在本文研究的基础上，未来的研究应在对现实问题更深入分析的前提下，考虑更多供应商或者多个制造商的情况，以建立更具有现实研究意义的模型；另外，多个供应商的博弈分析也是未来亟待解决的问题。