利用改进的3DMax算法重构染色体3D结构

刘立伟,么会丽

(大连交通大学 理学院，辽宁 大连 116028)

染色体构象捕获技术，特别是Hi-C技术的发展，使基因组空间构象的分析和研究成为生物信息学和计算生物学的重要课题。在高通量下一代测序技术的帮助下，Hi-C技术可以生成全基因组范围的、大规模的染色体内和染色体间相互作用数据，能够详细描述基因组内的空间相互作用。这些数据可以用来重建染色体的三维结构，用于研究DNA复制、基因调控、基因组相互作用、基因组折叠和基因组功能[1-9]。目前，根据构建染色体三维模型原理上的不同，可将结构模型分为两大类:即基于概率约束的预测模型和基于距离约束的预测模型。由于细胞染色体的三维结构是动态的，我们可以用一些概率分布来描述它，从而将染色体三维结构的构建问题转化为概率模型的构建问题。实现这一过程的方法称为基于概率约束的预测模型。其中有一些方法是通过两步来进行染色体基因组三维结构建模，即将Hi-C数据中片段对之间的相互作用频率(IF)转换为片段对之间的距离，然后通过对距离值进行优化，推断出最能满足距离的3D结构，即求解出染色体片段的三维空间坐标，实现这两步过程的方法称为基于距离约束的模型。在对距离值进行优化的过程中，常用梯度迭代优化算法优化目标函数，目前现有的随机梯度优化算法有SGD、Momentum、Nesterov、Adagrad、Adadelta、Adam、Adamax、Nadam[10-16]，本文根据目前存在的随机梯度优化算法的优点和缺点，提出了XNadam算法。

1 3DMax 算法原理简介

3DMax算法[17]是由Oluwadare等人提出，它使用最大似然方法从Hi-C数据中推断染色体的三维结构。3DMax比现有的大多数方法都要快，它只依赖于通过最小二乘残差来优化预测模型的结构坐标。3DMax算法也是基于距离约束的预测模型，该算法首先通过初始化一组染色体空间坐标，计算出染色体片段之间的欧氏距离，然后通过转换函数将输入的接触频率矩阵转换成的距离矩阵，并假设距离矩阵中的每一个数据点独立并服从正态分布，从而构建一个基于正态分布的对数似然目标函数，再采用梯度上升算法迭代优化目标函数直到算法收敛，在迭代过程中同步更新染色体三维坐标。在3DMax算法中，采用梯度上升算法对目标函数进行迭代优化的过程中，计算出距离斯皮尔曼相关系数(DSCC)，并选出最大DSCC系数对应的转换参数，最优转换参数下的染色体片段坐标，是我们推断出最能满足距离的可视化染色体结构。3DMax算法还有一个变体，称为3DMax1，它在输入噪声时对输入接触矩阵进行额外的预处理和滤波。

在3DMax1算法中，Oluwadare等人，使用的随机梯度上升算法是自适应梯度算法(AdaGrad)[18]。自适应梯度算法(AdaGrad)是一种基于梯度的优化方法，它可以使学习速率适应每个参数，可以对低频的参数做较大的更新，对高频的做较小的更新，也因此，对于稀疏的数据它的表现很好。它的缺点是分母会不断积累，内存需求较大，这样学习率就会收缩并最终会变得非常小，甚至趋于零。

2 XNadam算法原理简介

除了3DMax1算法中应用到的自适应梯度算法(AdaGrad)以外，目前现有的随机梯度优化算法还有SGD、Momentum、Nesterov、RMSprop、Adadelta、Adam、Adamx、Nadam。本文提出了一种新的随机梯度上升算法XNadam，是Nadam的一个变体。Nadam(Nesterov-acceler Adaptive Moment Estimation)是将Adam与Nesterov算法结合在一起，具备二者的优势。它对学习率的约束将更强，使得此算法在某些问题上效果更好。Nadam的优点主要在于经过偏置矫正后，每一次迭代学习率都有个确定范围，为不同的参数计算不同的自适应学习率，使得参数比较平稳，同时内存需求较小，也适应于大多非凸优化，适应于大数据和高维空间。由于加入了Nesterov项，则在梯度更新时做一个校正，避免前进太快，同时提高灵敏；XNadam作为Nadam的一个变体，原理跟Nadam类似。区别是XNadam采用正弦的相关方式进行学习率的衰减，同时利用正弦方式的衰减率对一阶矩估计进行修正，所以XNadam具有Nadam算法的所有优点。

3 XNadam算法

XNadam算法要求:初始学习率α0,最小学习率αmin要求:矩估计的指数衰减速率β2,β1,取值区间均为[0,1)内要求:用于数值稳定的小常数δ(默认10-6)要求:初始化一阶和二阶矩变量n=0,m=0,初始化时间步长t=0计算梯度:gt+1=‰f(St)对梯度更新:g^t+1=gt+11-∏t+1i=1βi1更新有偏二阶矩估计:nt+1=β2·nt+(1-β2)·g2t+1修正二阶矩的偏差:n^t+1=nt+11-βt+12更新有偏一阶矩估计:mt+1=β(t+1)1·mt+(1-β(t+1)1)·gt+1衰减速率:β(t)1=β1·0.5·(1+sin(tπT))T=t(t+3)2对一阶矩修正:m^t+1=mt+11-∏t+2i=1βi1继续修正一阶矩:m-t+1=β(t+2)1·m^t+1+(1-β(t+1)1)·g^t+1学习率:αt=α0·[(1-αmin)·0.5·(1+sin(tπT))+αmin]计算更新:ΔSt+1=αt+1m-t+1n^t+1+ε应用更新:St+1=St+ΔSt+1

4 模型相似性和准确性的测量

为了测试该算法，利用3DMaxAdaGrad，3DMaxNadam和3DMaxXNadam算法对酵母染色体三维结构进行重构，进而比较他们的性能。3DMaxAdaGrad、3DMaxNadam、3DMaxXNadam是3DMax算法的一个变体，其中3DMaxAdaGrad是结合了极大似然算法和AdaGrad算法预测模型，而3DMaxNadam是结合了极大似然和Nadam优化算法的预测模型，3DMaxXNadam是结合了极大似然和XNadam优化算法的预测模型。在比较的过程中，3DMaxXNadam算法中β1=0.6，β2=0.999 9，αmin=0.000 1，只有学习率是变化的。

本文采用距离均方根误差(Distance Root Mean Squared Error ，DRMSE)、距离斯皮尔曼相关系数(Distance Spearman Correlation Coefficient ，DSCC)、距离皮尔森相关系数(Distance Pearson Correlation Coefficient，DPCC)[19-22]来量化结构的相似性，从而衡量预测方法的性能。

在本研究中输入的归一化接触频率值所选择的数据集是酵母的Hi-C数据，酵母Hi-C数据用Yaffe和Tanay等人[23]提出的技术进行了归一化。3DMaxAdaGrad，3DMaxNadam和3DMaxXNadam算法对1-12号染色体三维空间结构重构的DSCC、DPCC 和DRMSE三个评价指标结果(见图1)。

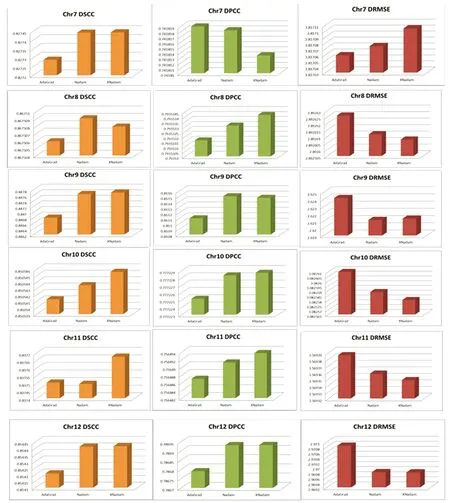
图1 3DMaxAdaGrad，3DMaxnadam和3DMaxnadam算法重构染色体三维结构的评估结果Fig.1 Evaluation results for 3DMaxAdaGrad, 3DMaxNadam, and 3DMaxXNadam

图1中的柱形图表示了3DMaxAdaGrad，3DMaxNadam和3DMaxXNnadam三种算法重构染色体三维结构的DSCC、DPCC和 DRMSE评估结果。第一列黄色柱形图代表三种算法对酵母1-12号染色体三维结构重构的DSCC结果，观察图形可知，对于1号、2号染色体，3DMaxAdaGrad算法重建染色体三维结构的DSCC值最大，其次是3DMaxXNnadam算法的DSCC值，其中3DmaxNadam算法的DSCC值最小；对于8号染色体，3DmaxNadam算法重构染色体三维结构的DSCC值最大，其次是3DmaxXNadam算法的DSCC值较大，最小的是3DMaxAdaGrad的DSCC值；除了上述三条染色体，其余的染色体都是3DmaxXNadam算法重构染色体三维结构的DSCC值最大。

第二列绿色柱形图代表三种算法对酵母1-12号染色体三维结构重构的DPCC结果，从图可以看出，除了7号染色体，其余11条染色体中，3DmaxXNadam算法重构染色体三维结构的DPCC值最大，其次是3DmaxNadam算法的DPCC值，最小的是3DMaxAdaGrad算法的DPCC值。

第三列红色柱形图代表三种算法对酵母1-12号染色体重构的三维结构DRMSE结果，从图可以看出，除了7号染色体，其余11条染色体中，3DmaxXNadam算法重构染色体三维结构的DRMSE值最小，其次是3DmaxNadam算法的DRMSE值，最大的是3DMaxAdaGrad算法重构染色体三维结构的DRMSE值。

根据上述实验结果可知，3DmaxXNadam算法的性能更好。

5 染色体三维结构可视化

通过算法比较，3DmaxXNadam算法对染色体三维结构进行重构具有较高的准确度。在此，使用该算法对酵母 1-12号染色体三维空间结构进行重构，得了酵母1-12 号染色体的三维效果图(见图2)。

图2 染色体的三维空间结构重构效果图Fig.2 Sketch of 3D structure reconstruction of chromosomes

6 结 论

本研究在Nadam优化算法的基础上发展了一种新的梯度上升优化算法(XNadam)，并引入最大似然算法分别和AdaGrad、Nadam、XNadam算法相结合得到3DMaxAdaGrad，3DMaxNadam和3DMaxXNadam算法。利用3DMaxAdaGrad，3DMaxNadam和3DMaxXNadam算法对酵母染色体三维结构进行重构，并且计算了生成的染色体优化结构的DSCC、DPCC 和DRMSE的值，从而衡量预测方法的性能。在真实数据集上的实验结果表明，3DmaxXNadam算法可以更有效地从Hi-C接触矩阵中重建染色体模型，同时与其他方法相比，它速度更快，对内存的要求也较低。这个结论说明新的梯度上升优化算法(XNadam)在优化对数似然目标函数上，它的表现比大多数其他优化方法更好。