悬索桥基准索股调整计算的改进方法
邓小康,孙 杰
(武汉科技大学 汽车与交通工程学院,湖北 武汉 430081)
0 引 言
悬索桥主缆索股架设线形控制是悬索桥施工控制的关键环节[1],主缆索股架设完成后,其在鞍槽内不动点位置就完全固定下来[2],后续施工中不动点间的无应力长度无法再进行调整,故对主缆线形存在的误差应尽量在索股架设阶段加以消除[3-5]。
主缆索股架设线形调整计算的核心是确定无应力索长调整量(ΔS)与垂度偏差量(Δf)之间的关系。文献[6]提出基于抛物线理论的基准索股调整计算方法,该方法计算简便、精确度较高,但其采用抛物线来拟合主缆线形,与实际情况并不相符。文献[7-8]提出基于悬链线理论的基准索股调整计算方法,该方法采用了与实际情况最为接近的悬链线来拟合主缆线形,但需通过反复迭代来确定主缆线形和无应力长度,计算繁琐,不便于现场调索操作[9-10]。
笔者在对悬索桥主缆线形和主缆变形与受力关系分析基础上,提出了一种悬索桥基准索股调整计算的改进方法。该方法基于悬链线理论,采用泰勒公式将主缆线形方程在目标空缆状态处展开,求解展开后的方程即可获得索长调整量与主缆跨中矢高变化量之间关系,该方法计算简便、精度高。此外,笔者还分别讨论了该方法在等高主塔和不等高主塔情况下的应用。
1 计算方法提出
主缆计算示意如图1。图1中:以最低点A为原点,y轴竖直向上,左边x轴水平向左,右边x轴水平向右建立坐标系。令:q为沿索长均匀分布的主缆自重,H为索段上任一点的水平分力,z为任一点的斜率。

图1 主缆计算示意Fig. 1 Schematic diagram of main cable
文献[11]已求出不考虑弹性伸长对主缆自重荷载集度影响时的主缆线形斜率参数方程和有应力长度。故图1中主缆线形方程如式(1)~式(3):
(1)
(2)
(3)
图1中的最低点左侧主缆(或右侧主缆),其任意两点间主缆有应力长度如式(4):
(4)
式中:zj为索段高点j的斜率;zi为索段低点i的斜率。
为计算简便,笔者在进行调索计算时,对当前状态和目标空缆状态的主缆长度均采用有应力索长。文献[12]研究表明:这样处理造成的误差很小。
2 等高主塔基准索股调整计算
等高主塔基准索股的调整计算可归纳为:已知在考虑各种施工误差情况下的主缆计算跨径为L,主缆在调索前的垂度为f(假定此时跨中标高高于目标状态Δf),沿索长均匀分布的主缆自重为q(图2),求主缆的索长调整量。

图2 等高主塔基准索股调整示意Fig. 2 Adjustment diagram of datum cable strand of constant heightmain tower
2.1 主缆调索方程构建
由于主塔等高,最低点A位于跨中位置,且此时A点往左右两边的斜率均为0。令调索前主缆顶端的斜率为z1,主缆水平分力为H。代入式(1)、式(3)可得式(5)、式(6):
(5)
(6)
式(5)、式(6)为二元非线性方程组,方程组包含两个未知数,即主缆的水平分力H和顶端的斜率z1,只需求出两个未知数,调索前的主缆线形和内力即可完全确定。式(6)除以式(5)得式(7):
(7)
构建函数如式(8):
(8)
式(8)即为对称主塔的主缆调索方程,其仅包含顶端斜率z1一个未知数。对式(8)求导得式(9):
(9)
对式(8)求二阶倒数,有式(10):
(10)
式(10)恒大于0,g(z1)为凹函数,如图3。
2.2 运用泰勒一阶展开式计算调索量
目标空缆状态下主缆长度S0和主塔顶端主缆斜率z0为已知量,均可由成桥状态分析得到[13]。

图3 g(z1)函数示意Fig. 3 Schematic diagram of g(z1)
由于调索前空缆状态和目标空缆状态主缆线形差别不大,z0应在式(8)的解附近,将g(z1)在z0处一阶展开,得式(11):
(11)
式中:O(z1)为高阶微量。
忽略高阶微量,则式(11)变为式(12):
g(z)=C1+C2(z1-z0)=0
(12)
求解式(12)即可求得z1,如式(13):
(13)
通过文中算例发现:采用泰勒一阶展开求出的z1存在较大误差,对结果按照式(13)进行二次修正后即可得到满足精度要求的z1。
将z1代入式(5)可求得调索前空缆状态主缆的水平分力H,如式(14):
(14)
将求得的H和z1代入式(4),即可得到有应力长度S。需注意的是,目标空缆状态的主缆长度S0也应采用不考虑变形前后q变化时的有应力长度,将S和S0相减,即得索长调整量,如式(15):
ΔS=|S-S0|
(15)
2.3 运用泰勒二阶展开式计算调索量
将g(z1)在z0处二阶展开,有式(16):
(16)
式中:O(z1)为高阶微量。
忽略高阶微量,则式(16)变为式(17):
(17)
式中:C1、C2同2.2节。
求解式(17),即可求得z1,如式(18):
(18)
将式(18)代入式(5),即可求出H。
已知z1和H即可参照2.2节方法求出当前状态下主缆长度S,并由式(15)得到索长调整量ΔS。
3 不等高主塔基准索股调整计算
为满足地形和线路走向要求,在某些情况下悬索桥会采用主塔不等高的设计[14]。不等高主塔会造成主缆线形改变和内力重分布[15],其调索计算方法也会发生改变。
不等高索塔基准索股的调索计算可归纳为:已知在考虑各种施工误差情况下的主缆计算跨径为L,主缆在调索前的左右垂度分别为f1、f2(假定此时主缆最低点标高高于目标状态Δf),沿索长均匀分布的主自重为q,求主缆索长的调整量,如图4。

图4 不等高索塔基准索股调整示意Fig. 4 Adjustment diagram datum cable strand of unequal height tower
令调索前左、右主缆顶端斜率分别为z1、z2,则主缆水平分力为H。由式(5)、式(6)可得式(19)~式(21):
(19)
(20)
(21)
由式(19)除以式(20)、式(20)除以式(21),可得式(22)、式(23):
(22)
(23)
对式(22)进行调整,有式(24):
(24)
对式(23)进行调整,有式(25):
(25)
目标空缆状态下主缆长度S0和主塔顶端主缆斜率z10、z20为已知量,均可由成桥状态分析得到。
由于调索前空缆状态和目标空缆状态主缆线形差别不大,z10、z20应在式(24)、式(25)的解附近。将m(z1,z2)和n(z1,z2)在(z10,z20)处一阶展开,得式(26)~式(31):
(26)
z20)+O2(z1,z2)
(27)
令:
(28)
(29)
(30)
(31)
式中:O1、O2分别为高阶微量。
将z1=z10、z2=z20代入式(28)~式(31),即可得到泰勒展开式的各项系数,忽略高阶微量,式(26)、式(27)可写为式(32)、式(33):
m(z10,z20)+C1(z1-z10)+C2(z2-z20)=0
(32)
n(z10,z20)+C3(z1-z10)+C4(z2-z20)=0
(33)
求解式(32)、式(33),即可求得z1、z2,如式(34)、式(35):
(34)
(35)
为提高精度,可将求得的z1、z2再次代入式(34)、式(35)进行二次修正,修正后的z1、z2作为最终结果。
将z1、z2代入式(19),可求得主缆水平分力H,如式(36):
(36)
已知z1、z2和H后即可参照第2节方法求出当前状态下的主缆长度S,再用|S-S0|即可求得索长调整量。
4 算 例
4.1 算例1
某等高主塔悬索桥,主缆沿弧长的自重线荷载为q=0. 2117 kN/m,已通过成桥状态线形分析得到主缆索股有应力长度为1 129.020 m,在考虑索塔偏位和索鞍预偏量情况下,实测索股两端水平距离为1 105. 622 m,目标空缆状态参数见表1。

表1 目标空缆状态参数Table 1 Parameters of target empty cable status
对跨中标高高于目标状态(即垂度小于目标空缆状态)0.2、0.4、0.5、0.6、0.8、1.0 m情况,通过悬链线索长计算程序得到当前状态精确索长及索长精确调整量(与文献[8]对比,其索长误差小于0.001%),再按照文中提出的改进方法和基于抛物线理论的调索公式分别计算主跨索长调整量,将这3者对比,结果如表2。
通过表2可看出:同精确解相比,基于抛物线理论调索公式计算结果误差为3.24%~4.35%;而采用文中基于泰勒公式一阶展开式(不进行二次修正)进行调索计算时,计算结果误差为8.70%~25.54%,误差较大;进行二次修正后,计算调索量误差降为0~1.09%,精度大为提高;采用文中提出的基于泰勒公式二阶展开式进行调索计算时,计算调索量误差为0~1.09%,索长调整量计算精度较高。
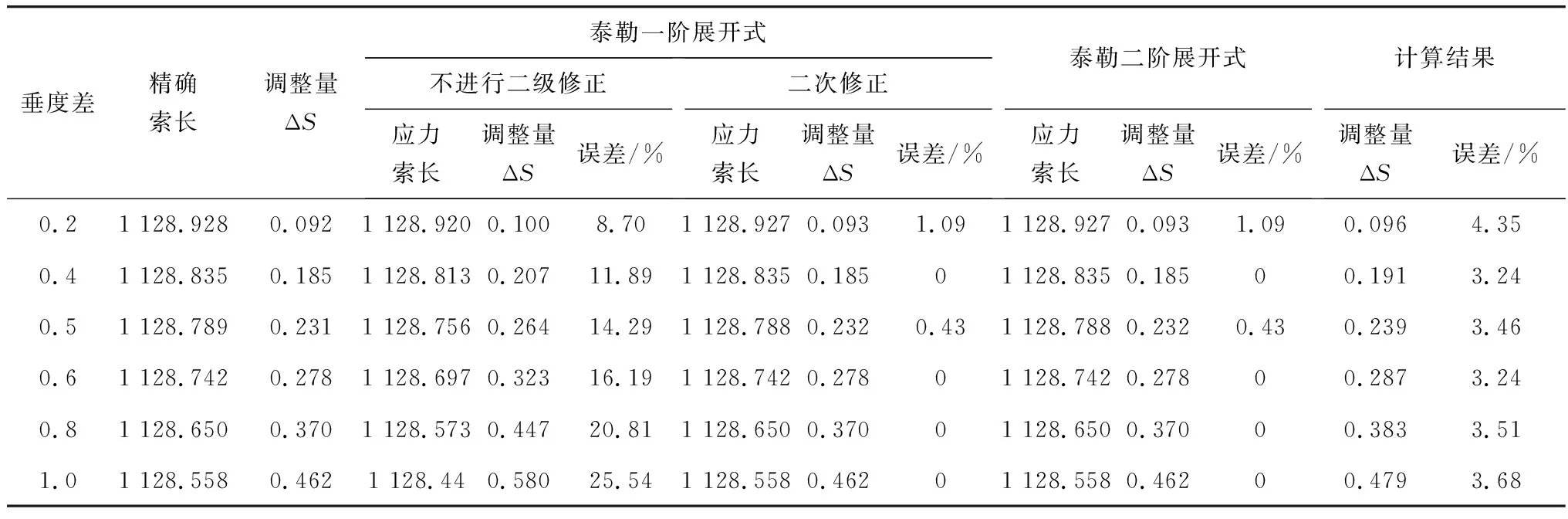
表2 等高索塔索长调整量比较Table 2 Comparison of cable length adjustment of equal height cable tower m
4.2 算例2
某不等高主塔悬索桥跨度L=888 m,主缆恒载集度q=54 kN/m,取f1=60 m,f2=61 m。对跨中标高高于目标状态(即垂度小于目标空缆状态)0.2、0.4、0.5、0.6、0.8、1.0 m的情况,通过悬链线索长计算程序得到当前状态精确索长及索长精确调整量,再按照文中提出改进方法的调索公式计算主跨索长调整量,将二者对比,结果如表3。
由表3可知:当主塔不等高时,同精确值相比,采用文中提出的泰勒公式一阶展开式(二次修正)进行调索时,计算调整量误差为0~0.32%,索长调整量计算精度较高。

表3 不等高索塔索长调整量Table 3 Cable length adjustment of unequal height cable tower m
5 结 论
笔者提出了一种悬索桥基准索股调整计算的改进方法。该方法以笔者前期研究过程中提出的主缆线形斜率参数方程和索长计算方法为基础,将当前状态主缆线形方程采用泰勒展开式展开,求解展开后的方程即可得到调索前主缆长度,进而获得索长调整量。
算例1结果表明:等高索塔采用泰勒公式一阶展开式(不进行二次修正)计算时,得到的索长调索量误差较大;采用泰勒公式一阶展开式(二次修正)或泰勒公式二阶展开式进行调索计算时,索长调整量与精确值基本一致。算例2结果表明:不等高索塔采用泰勒公式一阶展开式(二次修正)进行调索计算时,索长调整量与精确值基本一致。

