基于扫频振动门系统驱动电机壳体优化设计

王卫，贡智兵，谭文才，李锦伟，黄东盛

(南京康尼机电股份有限公司，江苏南京 210013)

0 引言

随着全球气温变暖，能源危机逐渐加剧，新能源城市公交车逐渐取代传统燃油公交车。电动内摆门相较于传统气动门省去了电能转化为气能然后再转气压能，更节能，噪声更小，因此电动门系统逐渐取代气动门系统广泛应用于公交车上，电动门上有电机作为动力输出驱动门系统的开关，是电动门系统中的关键部件，满足标准QC/678—2016《客车乘客门门泵》中规定的扫频振动试验是一项重要指标。

目前针对扫频振动试验零件破坏的研究主要集中于疲劳的计算方法。丁杰和张平[1]对电机控制器进行正弦扫频疲劳仿真，分析X、Y和Z3个方向的振动疲劳损伤，得出结构薄弱部位的疲劳寿命结果。最后借助振动试验检测，验证了仿真分析方法的可行性。周苏枫等[2-3]

提出了一种振动疲劳寿命预计的简便处理方法，在没有适用的结构材料疲劳S-N曲线的情况下，利用计算或试验测得的构件临界部位的响应功率谱密度曲线，根据疲劳损伤量等效原则和疲劳损伤可“累积”原则计算所对应的疲劳损伤量。李琳琳等[4]以骑跨式机架为研究对象，为避免机架产生共振,在发动机安装位置添加弹性元件，对机架采用减振方案的谐响应分析，计算得出应力、变形量的变化曲线，结合机架结构材料的S-N曲线和线性累积损伤理论,对机架进行疲劳分析。

文中以新能源大巴车电动内摆门门系统驱动机构电机壳体为研究对象，以振动试验标准和理论为基础，推导了扫频振动结构中某点振动疲劳损伤量。基于Workbench构建了有限元模型，进行扫频振动分析，结合线性累积损伤理论Miner以及扫频振动疲劳理论计算出扫频试验中电机壳体薄弱地方，并借助试验验证，对电机壳体进行结构加强改进，基于有限元仿真分析方法对新结构进行扫频耐振性分析，同时将新结构带入门系统进行门系统扫频试验，验证了该计算方法的可行性和可靠性。

1 振动试验标准

正弦振动试验是试验室中验证机械系统耐振性经常采用的试验方法，目前我国现行QC/T 678—2016《客车乘客门门泵》标准规定了对乘客室门系统耐振性能的要求[5]，标准中规定了扫频试验的振动方向和载荷严酷要求，如表1所示。

表1 扫频振动要求

参考环境试验标准GB/T 2423.10—2019中规定的扫频振动参数[6]为：

(1)

(2)

(3)

f=f1ekt

(4)

式中：L是振动循环次数；X是倍频程；T是一个扫频循环振动时间(f1→f2→f1)；f2和f1是扫描上限频率和下限频率；SR是扫频速率，倍频程/分钟(oct/min)。f为t时刻对应的频率，k为扫描速率，如果是每分钟一个倍频程，则k=ln2=0.693，所以公式(4)可以写成如下：

f=f1e0.693t

(5)

根据公式可得：从17 Hz开始扫频到200 Hz截止，振动总次数为15 840次，总时间为3.556 min，其中17～60 Hz范围内，振动次数为3 722次，振动时间为1.819 min；60～200 Hz范围内，振动次数为12 118次，振动时间为1.737 min。为研究扫频振动特性，等时间提取M个振动频率点作为研究对象，根据公式(5)可得此时扫频频率为：

(6)

(7)

式中：m为提取序号，m≤M；fm为提取序号m对应的频率；Nm为fm频率下振动次数。

2 正弦扫频振动疲劳计算

利用对数扫频方式进行振动时，线性系统结构某点的应变响应为:

ε(t)=A0sin{2π[f1ekt+φ0]}

(8)

式中：A0是应变幅值；φ0是应变信号的初相位；f1为扫频时开始激励频率；t为开始的时间。

课程主要分为通识教育课程，大学外语教育课程，专业教育课程，实践教学环节四个类别，着重提高大学外语教育课程，实践教学环节学分比例，同时提高选修课程比例，提高各模块选修课程学分比例，分别设置通识教育类、外语类、专业方向类、专业任选类、实验教学类选修课程，给学生提供更多的选择机会。具体课程类别与学分占比如表1：

由胡克定律可得：

σ=Eε

(9)

式中：σ为结构某一点处应力；ε为改点的应变；E为材料的弹性模量。

为分析简便，设正弦扫频时结构处于单向应力状态，且应力比K=-1，对应材料S-N曲线[7]为:

lgs=a+blgN

(10)

式中：s为结构的应力响应；N为对应于该应力响应的疲劳寿命；a、b分别是截距和斜率。

根据Miner累计损失理论，可以计算出在激励时间T后，结构的疲劳损伤量为：

(11)

由式(11)可以看出，当M趋近无穷大时，D收敛于一个常数，同理频率点取无限多时，结构某点的损伤值收敛于某常数。在结构弹性模量和S-N曲线不变的情况下，只要知道结构中某点应力响应就可估算出结构的疲劳寿命。

计算提取30个频率点，30个频率点对应的振动次数如表2所示。

表2 30个频率点对应的振动次数

表中各个频率点振动总次数为532 546，根据公式(1)计算出来为506 905，相对误差为5.05%。这主要是由于扫频试验时各个频率是连续的，而通过各个频率点计算出来的振动次数是离散的，但是相对误差只有5.05%，满足工程使用精度要求。

3 电机壳体扫频仿真

3.1 有限元模型建立

门系统物理扫频试验时，是将整个门系统进行扫频试验，为了研究门泵中驱动电机的耐振性能，节省计算资源，文中计算只将电机组件作为研究对象，如图1所示。电机组件主要由电机1、减速器盖板2、减速器壳体3、电机安装板4、传动齿轮5、机构固定板6等组成。主要零部件材料如表3所示。

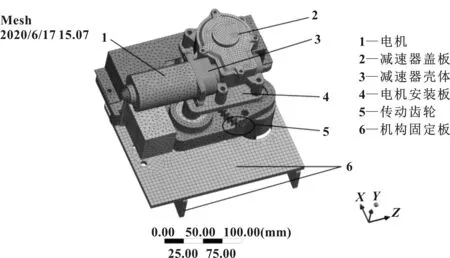
图1 原结构有限元模型

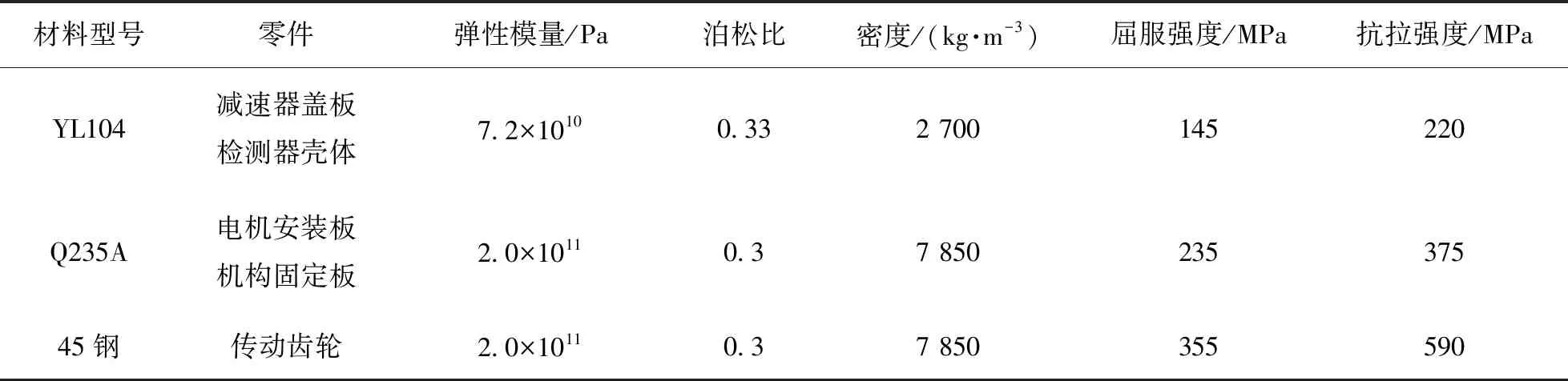
表3 有限元模型主要零部件材料属性

3.2 扫频试验仿真

扫频试验仿真主要应用有限元分析中的谐响应分析模块。谐响应分析主要且用于确定线性结构在承受随时间按照正弦变化载荷的稳态响应的一种技术，并可以得到一些响应对应的曲线。

QC/T 678—2016《客车乘客门门泵》标准规定扫频试验分为两段：一段是17～60 Hz,载荷为垂向0.35 mm，约束和载荷施加如图2所示，图中约束机构固定板X和Z向自由度，施加Y向位移载荷0.35 mm，扫描频率设置为17～60 Hz，完全法求解，阻尼设置为0.01;另一段扫频频率为60～200 Hz，载荷为垂向50 m/s2加速度，约束和载荷施加如图3所示，图中机构固定板端面全约束，如图中A所示，B为加速度载荷，用模态叠加法求解，阻尼设置为0.01。

图2 17～60 Hz约束和位移载荷施加

图3 60～200 Hz约束和载荷施加

3.3 扫频疲劳分析

3.3.1S-N曲线确定

驱动壳体所用材料为YL101，一次扫频试验循环次数为506 905次，位于1 000～1×107区间内，查阅相关资料[7-8],取a=520 MPa，b=-0.076，所以YL101S-N曲线如图4所示。

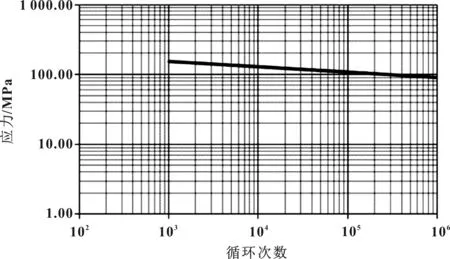
图4 YL101 S-N曲线

3.3.2 危险点确定

门系统扫频振动试验时，门泵机构驱动电机壳体发生断裂，断裂形式如图5所示。根据壳体断裂形式并结合力学分析可得,如图6所示4个点在扫频振动时受力较危险，将4个危险点进行疲劳计算。

图5 电机壳体断裂形式

图6 扫频振动时受力危险点示意

3.3.3 危险点应力提取

文中计算提取30个频率点，前6个频率点应力如图7所示，30个频率点对应的应力如表4所示。

图7 前6个频率点对应应力云图

表4 30个频率点对应的应力

3.3.4 计算累积损伤

疲劳累积损伤理论认为：当材料或零件承受高于疲劳极限的应力时，每一个循环都使材料产生一定量的损伤，在循环载荷作用下，疲劳损伤会不断累积，当损伤累积到达临界时发生疲劳破坏。线性累积损伤Miner理论形式简单、使用方便,在工程中得到广泛应用，线性累积损伤Miner理论认为材料在各个应力下的疲劳损伤是独立的，并且可以线性地累加起来，每次应力循环都会有损伤产生，当损伤值大于或等于1时，认为该结构则处于危险状态。根据计算公式(11)计算出4个点损伤值分别为0，352，2 559和0，其中点2和点3的损伤值远大于1 ，所以门泵系统驱动电机壳体扫频振动时会发生破坏，正好印证了第3.3.2节中扫频振动中电机壳体断裂形式。

4 结构改进及验证

4.1 结构改进

根据第3.3.4节计算可得，按照QC/T 678—2016《客车乘客门门泵》标准规定的扫频试验进行试验时，门泵电机壳体可能会发生破坏，现需要在材料不变的条件下对电机壳体加强优化。总共有3处结构需要优化：(1)将壳体壁厚由原来的3 mm增加到3.5 mm;(2)在侧边增加3 mm厚筋;(3)在壳体底部增加3 mm厚筋，如图8所示。

图8 优化前后结构比较

4.2 结构验证

对加强优化后的结构进行扫频仿真，边界条件与原结构分析相同，并根据第3.3.2节中确定的危险点，在优化后的结构中确定4个危险点作为衡量优化后结构的耐振性。4个危险参考点如图9所示。经计算4个点损伤值分别为D后1=0，D后2=0.23，D后3=0.38，D后4=0，4个危险点损伤值均小于1，所以基于扫频仿真获得结果判断优化后的结果满足耐振要求。将加强优化的电机壳体带入门系统进行扫频试验，电机壳体完好无损，门系统正常工作，说明优化后的结构满足扫频试验要求，验证了该计算方法的可行性和可靠性。

图9 优化结构扫频振动时受力危险点示意

5 结论

文中采用理论分析、数值仿真与试验相结合的研究手段，开展了新能源公交车电动内摆门驱动机构电机壳体扫频振动的研究得到如下结论：

(1)以扫频振动试验标准和振动疲劳理论为基础，介绍了振动扫频试验和扫频振动疲劳的计算方法，推导了扫频振动结构中某点的振动疲劳损伤量。

(2)为研究电机壳体扫频振动特性，可以将电机壳体组件作为研究对象，不必对整个门系统建模分析，提高了效率。

(3)基于理论计算和数值仿真对电机壳体扫频寿命进行分析，然后根据分析结果进行结构加强，最后利用理论计算和试验验证了这种方法的可靠性和可行性，也为后期结构优化提供参考，加快研发进度。