伸展褶劈理(C’面理)在递进变形过程中的行为及其对剪切带面理(S面理)的影响*

侯泉林 刘宏伟 郭谦谦HOU QuanLin, LIU HongWei and GUO QianQian

中国科学院计算地球动力学重点实验室；中国科学院大学地球与行星科学学院，北京 100049

伸展褶劈理(extensional crenulation cleavage，C’面理)是韧性剪切带中常见的构造面理之一，表现为一系列近平行的与剪切平面(C面或C面理)呈低角度斜交的剪切条带(shear band)，是可靠且重要的剪切指向标志(Agardetal., 2011; Simpson and Schmid, 1983; Whiteetal., 1980)。伸展褶劈理的发育可能对韧性剪切带中原本的流动状态施加了一个几何限制，可能加速剪切带的弱化，进而影响韧性剪切带中不同组分的递进变形行为。因此，其发育条件、发展过程和形成机理受到了地质学家的普遍关注(Fossen and Cavalcante, 2017; 侯泉林, 2020)。

White (1979)首先识别出糜棱岩中的共轭剪切条带。该条带大致以35°对称切割糜棱岩面理，面对缩短方向的共轭夹角为110°左右，且与整体剪切方向相反的一组发育程度远不如同向组(Zhengetal., 2004; Fossen, 2016)。同向剪切条带形似褶劈理，且与主剪切带的伸展相关，被称为伸展褶劈理(extensional crenulation cleavage)，为了使用简便用C’表示。自此，地质学家对伸展褶劈理的几何学、运动学特征进行了大量的研究，从不同角度探讨了其形成机制以及在递进变形过程中的行为(Zhengetal., 2004; Fossen and Cavalcante, 2017; 侯泉林, 2020)。

Blenkinsop and Treloar (1995)统计了C’面理与剪切带边界之间的夹角，发现这个夹角在统计学上呈现出集中分布的特征，并且旋转而造成的形态扭曲没有在C’面理上出现，因此认为C’面理在递进变形过程中不发生旋转。Zhengetal. (2004)同样统计了前人的数据，结合理论计算，认为C’面理出现在有效力矩最大的方向，与剪切带边界的夹角只与剪切带性质即运动学涡度有关，在递进变形过程中不旋转。

也有学者认为C’面理在递进变形过程中会随着应变的逐渐积累而旋转。Passchier (1991)认为，剪切条带与剪切带边界的夹角、剪切条带之上的剪应变、剪切条带之上的拉伸量以及体积变化之间存在函数关系，共轭的剪切条带在纯剪切作用下势必会背离最大缩短方向而旋转。Passchier and Trouw (2005)提到，C’面理的行为与C’面理之间的微劈石域的黏度大小有关，在微劈石域相对刚性的情况下，剪切条带与微劈石的旋转方向都将与整体剪切方向相反。Michibayashi and Murakami (2007)将发育在面理化层内的剪切条带称为层内剪切条带(intra-layer shear band)，切穿面理化层的剪切条带称为层间剪切条带(inter-layer shear band)，根据一个手标本尺度下剪切带内层内剪切条带与层间剪切条带相对剪切平面的角度随着应变大小的变化，认为层内剪切条带先形成，并且顺着整体剪切方向旋转，后期层间剪切条带在更低的角度上形成，并且由于层间剪切条带的活动，层内剪切条带不再活动。Finchetal. (2020)通过数值模拟计算认为C’面理的形成取决于整体剪切区域内软弱层(weak phase)的比例，软弱层的比例大于15%时最容易形成，并且C’面理是由于软弱层的变形而形成，软弱层旋转、集中分布形成的C’面理寿命短暂，一旦停止活动，C’面理就会反向旋转卷入C面理内。

此外，也有学者认为C’面理在递进变形过程中几乎不旋转。Platt (1984)计算了两种端元应变分配方式下C’面理的递进变形过程。当整体应变分解为沿着S面理的简单剪切、垂直S面理的纯剪切、旋转时，C’面理向剪切平面旋转；当整体应变分解为沿着C’面理的简单剪切、垂直C’面理的纯剪切、旋转时，C’面背向剪切平面旋转。因实际情况中这两种极端情况都不可能出现，因此认为C’面理很可能是“几乎不旋转的”。

由此可见，C’面理在递进变形过程中的行为和形成机理，及其对S面理行为的影响是长期存在争议的科学问题。递进变形过程中，剪应变逐渐增大是一个应变积累的过程。我们面对的地质体都是某一时刻的地质体，无法完整观察到这种应变积累过程，但是对于任一天然的剪切带而言，从其边缘到中心，剪应变逐渐增大，这种空间上的应变分布规律为理解时间上的应变积累过程提供途径。C面理在递进变形过程中不会发生旋转，已经是共识。本文统计了剪切带中不同部位C’面理、S面理和C面理的夹角，据此分析C’和S面理在递进变形过程中的行为；同时结合不对称布丁构造、侧生构造(flanking structure)等各向异性的面状岩石中应变特征的研究成果，分析S面理在C’面理形成后的变形方式；最后，从应变分配的角度探讨C’面理的形成机制。

1 几何学特征

假设C’面理与剪切平面(C面理)之间的夹角为α，S面理与剪切平面的夹角为β，C’面理与S面理之间的夹角为δ。三个角度之间有简单的数量关系(图1)：

α+β=δ

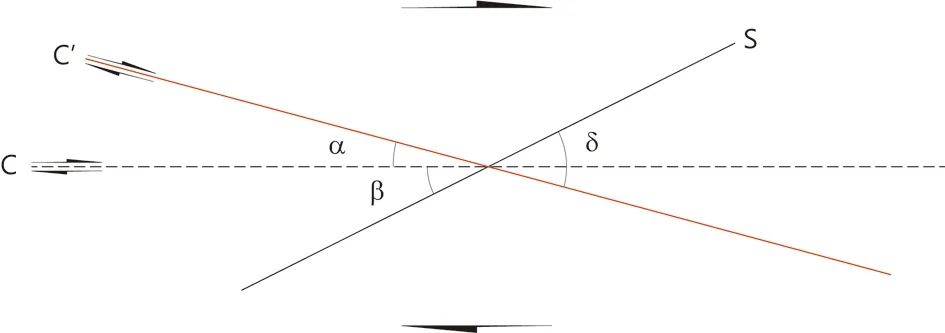
图1 韧性剪切带中的面理几何关系示意图Fig.1 Schematic diagram of the geometric relationship of the foliations in the ductile shear zone

本文测量了云蒙山大水峪韧性剪切带的相关角度，在Blenkinsop and Treloar (1995)、Zhengetal. (2004)的基础上，收集统计了不同剪切带中的α、β、δ值。

1.1 云蒙山大水峪韧性剪切带中伸展褶劈理的几何学特征

大水峪韧性剪切带发育于云蒙山变质核杂岩东缘，北东-北北东走向，紧邻主拆离断层(图2)。对该剪切带内花岗闪长岩的变形特征、变质变形温度、压力等的研究结果显示，从岩基到拆离断层面方向，石城剖面段，变形温度先降低后升高；云蒙峡剖面段变质变形温度逐渐降低，压力增大，剪应变逐渐增大；白道峪剖面段变形温度500℃以上，向南东逐渐降低；小水峪剖面段变形温度约480℃，向南东逐渐降低，同时剪应变逐渐增大(夏浩然, 2011; 张慧等, 2018; 赵腾格, 2020)。因此，本文重点观测了白道峪剖面段伸展褶劈理的形态学与运动学特征，测量统计了α、β、δ值(表1)。

白道峪剖面位于白道峪村村口，长约2km，糜棱岩面理倾向东南，152°～169°之间，倾角32°～37°之间，矿物拉伸线理倾伏向130°～140°之间，倾伏角30°～45°之间。该剖面出露有丰富的S-C-C’组构，且剖面中伸展褶劈理常呈近平行、等间距的单组出现，S面理与C’面理清晰可辨，S面理被C’面理所截，并且在C’面理附近发生了明显的变形与弯曲(图3a-d)。C’面理所在区域对应暗色矿物所在区域，可见暗色矿物与浅色矿物明显的差异风化现象(图3a)。C’面理在面理化区域内发育完整，而在未面理化区域内则未见完整的形态(图3c, d)。据S面理的连续性，可将C’发育程度分为相对较高和较低两种。

发育程度相对较低的C’面理附近，S面理发生细颈化，原有的连续性得到了不同程度的保留，可以观察到C’面理两侧的S面理有不同程度的连结(图3d)，形态类似于缩胀构造或者不对称布丁构造，S面理仍保持其连续性，C’面理之间S面理的弯曲形态指示S面理本身的旋转方向可能与整体剪切方向相反(图3d)。镜下同样可见S面理在C’面理处发生细颈化，仍然保持其连续性，剪切变形强烈，伴生有形态复杂的δ型旋转碎斑(图4a)。S面理在C’面理处形态仍旧显示，C’面理的运动学方向与整体剪切方向相同(图3a, b, d、图4a, c)。

发育程度较高的C’面理形态平直，具有一定的宽度，暗色矿物集中分布在C’面理区域内，原有形态已被强烈的剪切变形破坏殆尽，S面理在C’面理附近尖灭消失，收敛进入C’面理区域内(图3c)。显微镜下内部矿物的形态不可辨认，S面理被C’面理所截断，其原有的连续性被破坏，并且在C’面理附近发生偏转与滑移，变细尖灭卷入C’面理区域内，相对错动的方向显示C’面理的运动学方向与整体剪切方向相同(图4b, d)。C’面理附近剪切变形特征强烈，显微镜下可以观察到形态复杂的δ型旋转碎斑，有两组拖尾系显示两组不同的旋转方向(图4b)。

本文对白道峪剖面内广泛发育的C’面理、S面理以及C面理的几何参数(图1)进行了统计。自岩基到拆离断层面的方向上，选取650m长的剖面，以50m为间距，近等距选取14个点进行观察，每个观察点在不同位置测量三组数据，取平均值消除误差。随着测量位置距离剪切带中心越来越近，应变逐渐变大，α的大小保持相对稳定，β则逐渐增大，δ也逐渐增大。在数据分布特征上，α集中分布在19°左右，范围在16°～23°之间，β的范围在12°～26°之间，δ则位于32°～48°之间(表1)(图5a-f)。

图2 云蒙山地区地质概况以及剖面线路位置示意图(据陈印等, 2014)①石城剖面；②云蒙峡剖面；③白道峪剖面；④小水峪剖面Fig.2 The geological general situation of Yunmengshan area and the map of section route position (after Chen et al., 2014)

图3 白道峪剖面内发育的各种形态的S-C-C’组构(a)风化严重的S-C-C’组构；(b)发育程度很高的C’面理；(c)可见C’面理无法延伸到弱的面理化层内；(d)发育程度相对较低的C’面理. 笔为比例尺Fig.3 S-C-C’ fabrics in Baidaoyu section

图4 白道峪剖面中发育的伸展褶劈理的显微形态(单偏光下)(a)发育程度较低的C’面理，S面理仍旧保持其连续性，δ型旋转碎斑指示C’面理的运动学方向为上部向右；(b)发育程度较高的C’面理之间的δ型旋转碎斑形态复杂；(c)C’面理发育程度较低，S面理仍旧保持其连续性的；(d)发育程度较高的C’面理，S面理被截断Fig.4 The microscopic morphology under PPL of the extension crenulation cleavage in Baidaoyu section

图5 伸展褶劈理相关面理夹角统计及其与剪切带中心距离关系散点图为不同夹角距离剪切带中心的变化，柱状图为角度计数.(a-f)大水峪剪切带；(g)日本Shiwaku岛HT/LP变质带中的花岗糜棱岩(Michibayashi and Murakami, 2007)；(h)西班牙南部Nevado-Filábride Complex的剪切带(Jabaloy et al., 1993)；(i)西班牙Betic造山带中的Filabres剪切带(Agard et al., 2011)Fig.5 Schematic diagrams illustrating distributions of angles between different foliations in different shear zones

1.2 前人数据统计

Platt and Vissers (1980)对Betic Movement Zone内发育的伸展褶劈理进行了几何学统计，得出C’面理与剪切平面之间的夹角范围为20°～40°(均值29.4°，标准差9.3°，75个样本)。Jabaloyetal. (1993)对西班牙东南部Betic Cordillera一处剪切带内发育的C’面理进行几何学统计工作发现，C’面理与C面理之间的夹角有优选角度，且优选角度小于40°(表2；图5h)。Blenkinsop and Treloar (1995)对津巴布韦Mushandike发育的S-C-C’组构进行的统计学工作表明，C’面理与C面理之间的夹角大小范围为15°～25°(38个样本)(表2)。Zhengetal. (2004)对已有的研究中涉及到的数据进行整理，C’面理与糜棱岩面理(即C面理)之间的夹角范围通常在15°～35°且最大为35°(表2)。Michibayashi and Murakami (2007)在其研究中针对一块手标本中发育的C’面理给出的统计数据表明，C’面理与C面理之间的夹角小于20°(表2；图5g)。Agardetal. (2011)同样对西班牙Betic Cordilleras拆离面周边韧性剪切带中发育的C’面理进行统计，发现在长约700m的剖面上，C’面理与C面理之间的夹角范围为15°～35°(表2)。

Agardetal. (2011)对西班牙Betic Cordilleras主拆离面下韧性剪切带内D3变形期内形成的C’面理与D2变形期内形成的S面理之间的夹角δ进行了统计，从韧性剪切带边界到中心长700m的剖面上，δ的大小从10°增大到接近35°(表3；图5i)。Michibayashi and Murakami (2007)对仅发育层内剪切条带(intra-layer)的S面理与C面理的夹角β进行统计，从边界到中心25mm的范围内，夹角β的大小从45°减小到接5°左右(表3)。

表2 C’面理与C面理的夹角统计

2 伸展褶劈理的递进变形行为及其形成机制探讨

2.1 C’面理的递进变形行为

自然界中很难观察到递进变形的应变积累过程，而在同一个剪切带中，应变向剪切带中间增大(Fossen and Cavalcante,2017; Ramsay, 1980)。因此，本文近似的用剪切带不同部位C’面理与C面理之间夹角的变化代表递进变形过程中C’面理相对C面理的旋转方式和程度。对于任一确定的剪切带，当应变逐渐增大时，若α保持不变，则表明伸展褶劈理即C’面理在递进变形过程中不发生旋转；反之不论是α是增大还是减小，均表明C’面理都将随着应变的积累而发生旋转，呈现被动面理的特征。

表3 伸展褶劈理相关面理夹角的统计数据

对收集的α值进行统计分析，结果显示同一条剪切带中α值总体呈现近正态单峰式分布特征，不同剪切带中α的分布呈现相同的特征，但是具有不同的峰值。这种单峰式集中分布且不随应变大小变化的特征表明α在递进变形过程中相对稳定，也就是说C’面理在递进变形过程中并不发生旋转。

2.2 S面理的递进变形行为

β值的统计分析显示，自剪切带边界到中心，在不发育C’面理的情况下，β逐渐减小但不趋近于0，即S面理顺向旋转；然而，在发育C’面理的情况下，β反而随应变的增大而逐渐增大，同时S面理呈现左低右高的宽缓形态，表明在递进变形过程中S面理发生了反向旋转。

剪切条带型不对称布丁构造与韧性剪切带中伸展褶劈理体系具有相似性，主要体现在： C’面理与C面理的夹角较小，最常见的范围在15～35度，而被剪切条带所隔开的不对称布丁，其剪切条带与整体C面理的夹角为24°(340个样本，均值)(Goscombeetal., 2004)；剪切条带的运动学方向与整体剪切方向同样是相同的(Hanmer, 1986)(表4)；韧性剪切带中，C’面理发育之前，S面理是连续的，但C’面理发育之后，S面理被C’面理所截，类似于布丁化，发生伸展作用，变得不连续；C’面理的运动学特征与不对称布丁之间的剪切条带是相同的；均与剪切面(C面)呈低角度斜交。据此，C’面理的形成过程实际上可能也是S面理布丁化的过程。剪切条带型不对称布丁构造中的各布丁块在递进变形过程中会发生与整体剪切方向相反的旋转，即反向旋转(Fossen, 2016; 侯泉林, 2020)。这一旋转行为和机制可能与C’面理发育后S面理的反向旋转相同。

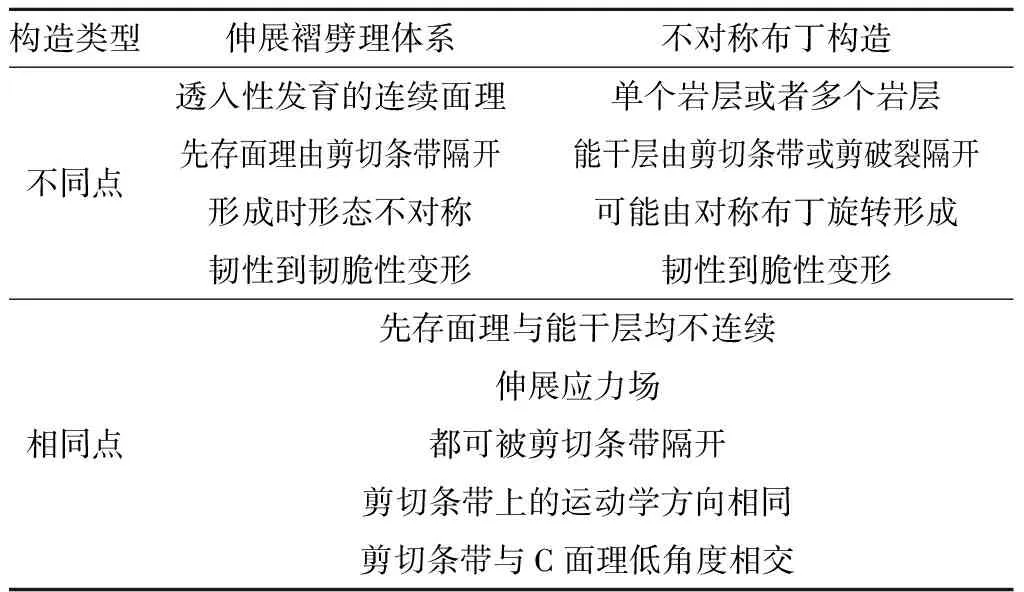
表4 不对称布丁构造与伸展褶劈理的比较

图6 简单剪切(a)、纯剪切(b)、一般剪切(c)情况下分层的运动学涡度以及ISA方向与β的关系(据Ishii, 1992)Fig.6 Kinematic vorticity of delamination under simple shear (a), pure shear (b) and normal shear (c) and the relationship between ISA direction and β (after Ishii, 1992)

Grasemannetal. (2003)利用二维有限元数值模拟研究侧生构造递进变形行为的成果显示，当异质体为有限长度的裂隙，与剪切平面的初始角度小于30°时，在运动学涡度从0到1即整体剪切从纯剪切到一般剪切范围内，寄主元素的偏转方向均与整体剪切方向相反，形成与伸展褶劈理形态十分相似的剪切条带型侧生构造(shear band type)。C’面理与C面理的夹角最常见的范围在15°～35°，假如S面理布丁化形成的断面和C’面理平行，那么根据剪切条带型侧生构造的模拟研究，S面理断开后很可能会发生反向旋转。

综上，据β值的统计特征、S面理和各向异性岩石有限应变特征的类比，本文推测，递进变形过程中，S面理随着应变增大向剪切方向旋转，C’面理形成后，S面理反向旋转。

2.3 应变分配模型对伸展褶劈理成因机制的启示

均匀变形的观点认为，在压剪性区域(一般剪切)内，纯剪切组分与简单剪切组分会均匀分布在整个变形区域内。但是假如压剪性区域内的岩石存在各向异性，那么整体的剪切变形就会分解为若干个不同性质的纯剪切或者简单剪切的子区域，这就是应变分配(Strain partitioning)(Jones and Tanner, 1995)。由于岩石存在原生或者次生的各向异性，应变分配现象出现在各种不同尺度的构造变形之中(Bell, 1985)。局部变形场与整体变形场可能有很大的出入(Jiang, 1994)，对于能干性相对强的层而言，其本身的变形会尽可能维持共轴变形，而能干性相对弱的层而言，其本身的变形则会尽可能维持非共轴变形(Lister and Williams, 1983)。

Bell (1985)指出，在变形的变质岩中，形状变化不明显的变斑晶几乎没有发生过旋转，那是因为应变分配发生后，简单剪切组集中分布于菱网状的狭长区域内，并且菱网状区域与C面理呈低角度斜交。Jones and Tanner (1995)给出的应变分配模型表明，在压剪性质的区域内(类似于一般剪切的剪切带)，如果一旦出现活动的走滑断层，那么断层之间的部分将几乎只受到纯剪，而简单剪切几乎全部被分配在了断层之中，并且据此成功地解释了圣安德烈斯等大型走滑断层两盘的逆断层产状不协调的问题。这与传统构造地质学中均匀变形的观点不同的是，薄弱面的存在承担了简单剪切组分，而不是薄弱面作为物质面一样随着整体的一般剪切而发生旋转。对湖北铁山不对称鱼嘴布丁构造的有限应变测量显示，基质层中靠近布丁体断开处，纯剪切占优势；靠近布丁体连续处，简单剪切占优势，反映了天然应变中应变分配的发生(曾佐勋等, 2013)。

Ishii (1992)进行了二维平面应变条件下的数值模拟，对强弱互层的材料施加纯剪切、一般剪切和简单剪切的模拟，初始条件主要涉及强弱层之间的黏度比、强弱层之间的厚度比，以及层面与剪切平面的初始角度等参数。结果发现，不同初始条件会影响到强弱层之间的应变分配情况。特别是当强弱层厚度比为1，黏度比为10时，整体剪切性质和粘性层与剪切平面间的初始角度共同决定了应变分配的具体情况(图6; 原文中为θ，为方便描述，引用时改为β。考虑到对称性，本文仅讨论β≥0°的情况)。

理想简单剪切条件下，当β=45°时，应变分配的程度最高，黏度高的层接近纯剪切变形，而黏度低的层运动学涡度甚至大于1，形成超简单剪切(图6a)。

在理想纯剪切条件下，当β=45°时，同样达到最大程度的应变分配现象，此时黏度高的层运动学涡度接近于无穷大，为刚体旋转，而黏度低的层则为一般剪切，运动学涡度约为0.6。但是随着β值降低，黏度高的层的运动学涡度迅速降低，黏度低的层的运动学涡度则缓慢降低。当β<20°时，二者均为近纯剪切状态(图6b)。

在一般剪切条件下(简单剪切组分与纯剪切组分各占一半)，当β=58°时，高粘度层反而具有极高的非同轴度，其上的运动学涡度接近于无穷大，本身的变形近似于刚体旋转，而低粘度层反而更接近于纯剪切变形。但是随着变形的进行，β逐渐减小，高粘度层的非共轴度急剧下降，低粘度层的非共轴度逐渐上升。当β减小到30°时，强弱层的运动学涡度相等。在β<20°时，高粘度层的运动学涡度接近于0，低粘度层的运动学涡度接近于1，整体一般剪切中纯剪切组分绝大部分被分配于强硬层上，而软弱层则吸收了绝大部分的简单剪切组分。

β以及ISA与剪切平面的夹角βs之间的大小关系可以表明层在特定情况下的旋转方向：βs小于β时，正向旋转，反之则反向旋转；在βs-β图中，以βs=β为界，位于该直线之上，反向旋转，位于该直线之下，正向旋转(图6)。

简单剪切、纯剪切、一般剪切三种情况下，直线与曲线的交点分别为30°、0°、10°。纯剪切情况下，强硬层A不会反向旋转；简单剪切情况下，强硬层与剪切平面夹角小于30°以后，开始反向旋转；一般剪切情况下，强硬层与剪切平面的夹角小于10°才会发生反向旋转(图6)。特别是，当一般剪切条件下，β=10°时，强硬层与软弱层之间的运动学涡度已经发生了明显的分异，强硬层的运动学涡度约为0.2，为近纯剪切变形，而软弱层的运动学涡度约为0.7，为典型的一般剪切(简单剪切组分近50%)。该实验说明，在整体剪切为一般剪切的情况下，强弱互层的材料，强硬层与剪切平面之间的角度β减小到一定程度(角度范围为10°～30°)后便不再继续减小，造成这种结果的主要原因就是应变在强弱层之间的分配作用(图7)。由此，本文推测，S面理旋转到一定角度后(10°～20°)不再继续旋转，并由于分配了更多的纯剪切布丁化，形成C’面理，应变重新分配，S面理反向旋转。

图7 韧性变形中的应变分配图示Fig.7 Schematic diagram of strain partitioning phenomena under ductile deformation

图8 简单剪切、纯剪切、一般剪切情况下不同粘性层的运动学涡度Fig.8 Kinematic vorticity of layers under simple shear, pure shear and general shear conditions

Passchier and Trouw (2005)的研究表明，在一般剪切条件下更容易形成C'面理。因此，C'面理可能是在一般剪切条件下的递进变形过程中强烈面理化的非均匀岩石中高黏度物质层逐渐被分配了更多的纯剪切组分，而低黏度层则被分配了更多的简单剪切组分的结果(图8)。在整体剪切变形初期，面理化层发生顺向旋转；随着递进变形过程的应变积累，面理化层与C面理之间的夹角逐渐减小，低角度(<30°)下应变分配模式开始发生转变，S面理被分配了更多的纯剪切组分，并且在纯剪切作用下，强的面理化层内部逐渐形成微型剪切条带；随着递进变形的进一步持续，微型剪切条带不断扩展形成C’面理，此时应变分配的形式再次发生了变化，C’面理被分配以绝大部分简单剪切组分。至此，整体的一般剪切作用分别被分解为S面理上的纯剪切和C’面理上的简单剪切，C面理本身不再有剪切作用，因此C’面理不会发生旋转。S面理被C’面理所围限，其行为受控于C’面理，发生与整体剪切方向相反的旋转，即反向旋转。

由此可以看出，递进变形过程中C’面理是否旋转之争本质上是均匀变形与应变分配之争。

认为C’面理在递进变形过程中发生旋转的研究者是从传统的均匀变形的角度出发，认为C’面理形成时的初始位置与最大主应力的夹角为45°，也就是说C’面理形成于剪应力达到最大的位置，而后在递进变形过程中发生旋转，背离最大压缩方向(Passchieretal., 2005)。在这种观点中，C’面理的发育并没有对原有岩石的力学性质产生改变，其行为如同被动面理S面理一样，受到递进变形过程中整体剪切流场的影响而旋转。然而，C’面理实际上并不是物质面，而是剪应变高度集中的剪切条带。

认为C’面理不旋转的研究者则认为，C’面理形成后成为简单剪切的主要载体，总应变中简单剪切被C’面理的剪切活动所吸收，而纯剪切则被S面理所吸收。国内学者郑亚东提出了岩石变形的最大有效力矩准则(Maximum Effective Moment Criterion, 缩写为MEMC)，通过计算认为C’面理形成时的初始位置仅与剪切带的性质有关，在递进变形过程中不发生旋转，是剪切带流场中固有的特征方向，出现在力矩最大的方向上(郑亚东, 1999; Zhengetal., 2004, 2015; 郑亚东等, 2007)。

3 结论

从以上分析可以得出如下结论：

(1)在韧性剪切带内，从边缘向中心随着应变逐渐增大，C’面理与剪切平面(C面理)的夹角保持稳定，表明C’面理在递进变形过程中不旋转。

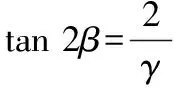
(3)随着递进变形的进行，S面理与C面理的夹角逐渐减小，强硬层分配了更多的纯剪切而逐渐布丁化，进而内部产生微型剪切条带，逐渐扩展形成初始的C’面理，随之C’面理被分配以更多的简单剪切。至此，随着应变分配的完成，C面上的剪切作用自行消失而失去对C’面理的制约， 故C’面理不发生旋转；然而S面理在C’面理的制约下开始反向旋转。

致谢对两位审稿人的精心审核，在此表示衷心的感谢。

为学一生中际逢良师何其有幸，谨以此文表达我及我的学生对恩师李继亮先生的敬意和深切怀念。