逆变器有限集模型预测控制参数不匹配补偿方法研究

唐圣学，邢路铭，黎霞，姚芳

(1.河北工业大学 河北省电磁场与电器可靠性重点实验室，天津 300130；2.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室，天津 300130)

0 引 言

近年来，有限集模型预测控制(finite control set-model predictive control, FCS-MPC)在功率变换、电机驱动等领域得到了广泛应用[1]。相较于传统的线性控制、滞环控制等，FCS-MPC通过滚动优化和在线寻优，省去复杂的调制环节，具有响应速度快、控制原理简单等优点[2]。

目前，逆变器FCS-MPC研究的主要成果有：文献[3]应用FCS-MPC实现了对三相逆变器电流控制，方法简单且易于实现；文献[4]和文献[5]使用FCS-MPC实现了多电平逆变器和多相逆变器的控制；文献[6-7]使用FCS-MPC实现对电机的转矩直接控制；文献[8]将FCS-MPC应用于脉宽调制整流器实现了功率控制；文献[9]将FCS-MPC应用于光伏发电逆变系统中，实现了光伏系统并网的有效控制；文献[10]通过筛选最佳的电压矢量研究了FCS-MPC开关损耗高的问题；文献[11-12]将MPC与准Z源网络结合起来，实现了逆变器的升降压FCS-MPC控制；文献[13]通过在目标函数中加入稳定电容电压的分量，研究了不平衡电网条件下的逆变器FCS-MPC控制；文献[14]研究了使用最优开关序列的方法来固定FCS-MPC的开关频率，以利于滤除谐波；文献[15]使用FCS-MPC实现了对电压型逆变器共模电压尖峰抑制；文献[16]将粒子群算法与FCS-MPC结合起来优化了权重系数设计。综上可见，FCS-MPC可有效应用于各种功率变换器控制中，具有灵活、适应性强的优点，可有效实现逆变器控制。

然而，实际运用FCS-MPC实现逆变器系统的目标优化预测控制，需要获取精确的预测模型。但是，预测模型中的电感、电阻受到电网或其他因素影响，难以精确获取，会导致预测模型参数不匹配，造成控制精度的下降。文献[17]讨论了电阻和电感不匹配对三相逆变器控制效果的影响，但是没有给出改善模型失配的补偿策略；文献[18]通过构造一个扰动观测器削弱了电感参数不匹配对控制效果的影响，但是控制方法复杂，没有考虑电阻和延时影响；文献[19]采用参数估计的方法获得电感实际值，但同时需要设计一个低通滤波器，补偿电路较复杂；文献[20]分析了电感不匹配对控制性能的影响，提出了电感在线辨识的方法，但是缺少对电阻的分析和辨识补偿。同时，由于FCS-MPC需要进行大量的选优计算，需要较长的计算时间，且采集电流等数据也需要时间，采样和计算延时也会造成控制效果变差[21]。实际上，延时与参数不匹配在FCS-MPC中同时存在，需要同时补偿才能更好地提高控制效果。

本文以单相逆变器控制为例，针对模型不匹配导致的FCS-MPC预测性能下降问题，分析了参数不匹配对预测电流误差的影响，研究了基于递推最小二乘法(recursive least squares，RLS)在线识别电感和电阻模型参数的方法，以及参数不匹配和延时协同补偿方法，设计了协同补偿策略，并进行了实验和仿真验证，取得了较好的实际效果。

1 逆变器有限集模型预测控制及误差分析

1.1 有限集模型预测控制

FCS-MPC基本过程为：根据被控系统的离散数学模型预测系统变化，利用目标函数最小化的寻优策略选择控制变量，实现每个采样周期滚动优化控制目标，是一种基于模型的闭环优化控制策略。下面以单相逆变器控制为例，说明FCS-MPC的实施原理。

图1所示为单相逆变器控制系统的结构图，图中：逆变器直流母线电压为UDC；输出电流为i；输出电压为u；R为线路电阻；L为滤波电感；C为滤波电容；e为负载反电动势或并网电压。

由图1知，忽略滤波电容，根据基尔霍夫定律可得逆变器系统电流i与电压u方程为

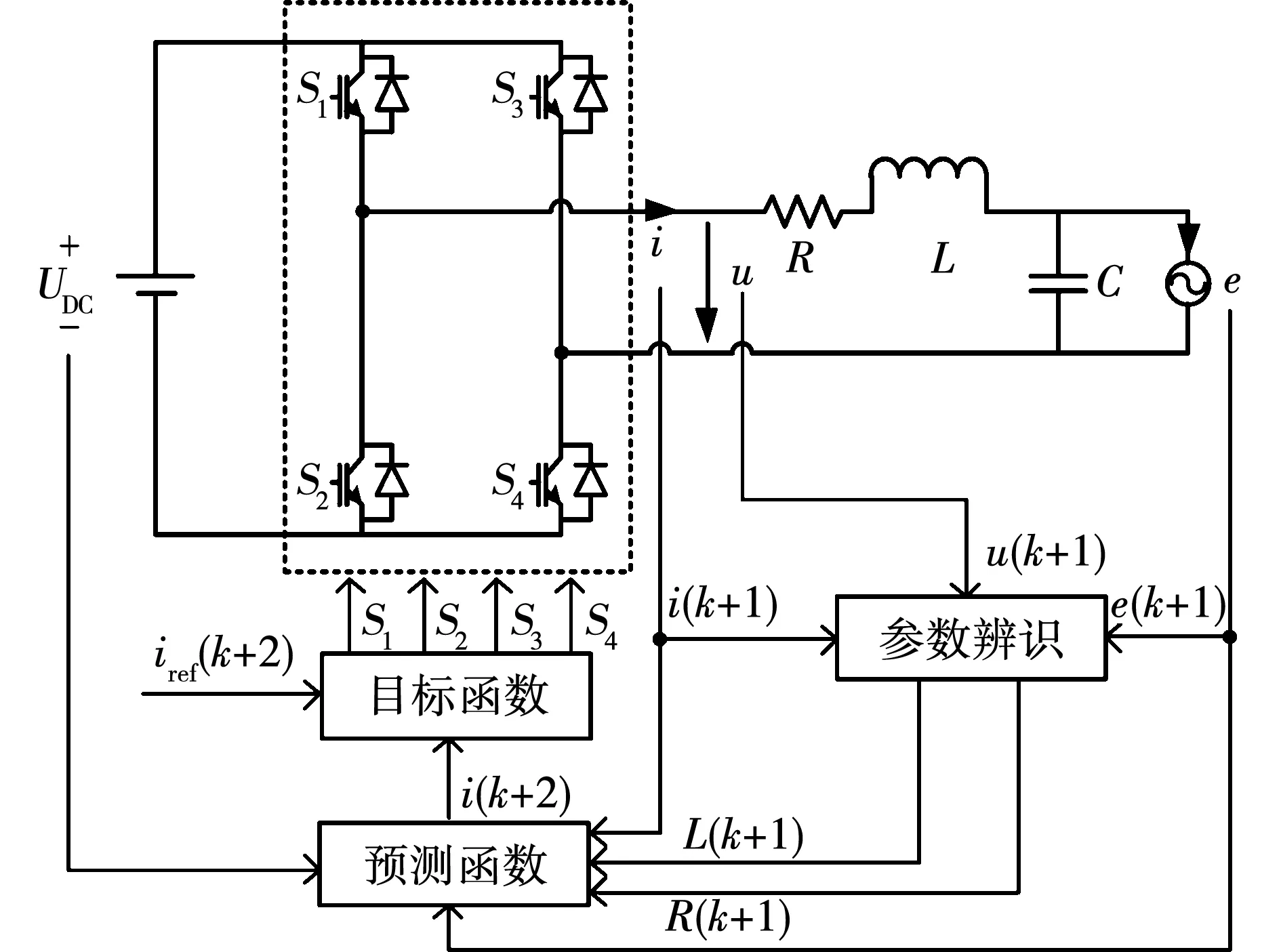
图1 单相逆变器控制系统结构图Fig.1 Control structure of single phase inverter

(1)

定义逆变器开关状态(S1,S2,S3,S4)为

(2)

为了避免逆变器上下桥臂直通短路，同桥臂开关不能同时开通，因此单相逆变器只有4种开关状态，4个电压矢量Vj(j=1,2,3,4)如表1所示，其中电压矢量V1和V4均为0。因此，为了简化分析，文中选择V1、V2和V3为备选电压矢量。

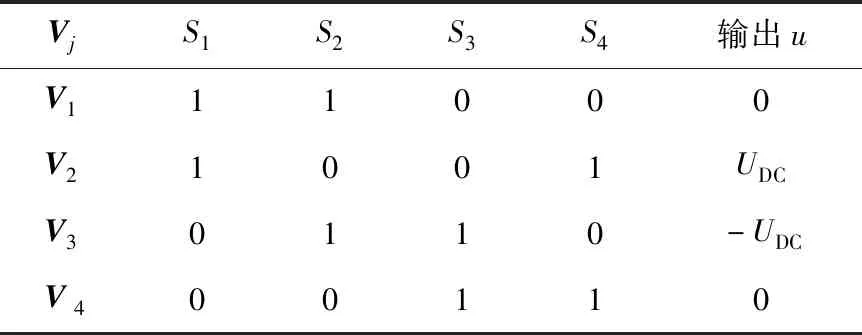
表1 电压矢量Table 1 Voltage vectors

设采样周期为Ts，由式(1)可得系统离散方程为

(3)

式中：i(k+1)为k时刻的预测电流；i(k)、u(k)、e(k)分别为k时刻逆变器输出电流、输出电压和负载电源电压。

根据式(3)，可得在电压矢量Vj(j=1,2,3)作用下k+1时刻的逆变器预测电流为

(4)

定义预测目标函数为

g=|iref(k+1)-i(k+1)|。

(5)

式中iref(k+1)为k+1时刻的参考电流。

FCS-MPC控制思路是选取使目标函数g最小的电压矢量Vj(k)为k时刻逆变器输出电压矢量，并滚动优化上述目标函数，可以实现逆变器输出控制。

根据式(4)可知，k时刻预测电流i(k+1)的预测精度与模型参数R、L和电压矢量Vj(k)相关。然而，实际参数R、L与预测模型式(4)中参数不相等、不匹配会造成控制性能下降。参数不匹配主要由元件容差、测量误差等引起。此外，电感还容易受实际运行中电压、电流等物理量的影响而发生改变，产生不匹配。

同时，式(4)中预测电流i(k+1)由k时刻数据寻优的电压矢量Vj(k)在k时刻作用下产生，从数据采集生成到获取最优电压矢量Vj(k)的处理时间默认为0。然而，实际上这期间存在延时，即数据采集和寻优计算处理需要时间。这些延时也会造成预测误差及控制性能下降。延时导致的误差分析及其影响不再阐述，可参考文献[21]和文献[22]。下面主要定量和定性分析参数不匹配导致的预测性能下降问题。

1.2 参数不匹配误差分析

设预测模型中的电感为L0，实际电感为L1，预测模型中的电阻为R0，实际电阻为R1，那么根据预测模型预测的输出电流为

(6)

实际模型预测输出电流为

(7)

定义电流预测误差为

Δi=i0(k+1)-i1(k+1)。

(8)

将式(6)和式(7)代入式(8)可得

ΔL(u(k)-e(k))]。

(9)

式中：ΔL=L1-L0；ΔR=R1-R0。

由式(9)可以看出，电流预测误差Δi与电阻匹配误差ΔR和电感匹配误差ΔL有关。电流预测误差Δi与前一时刻状态无关，即预测电流误差不存在累积效应。

由式(9)可见，Δi同时还受当前k时刻输出电流i(k)、输出电压u(k)以及电网电压e(k)影响。此外，式(9)中第二项ΔL(u(k)-e(k))相较于第一项(ΔRL0-ΔLR0)的幅值更大，Δi主要受此影响。

建立图1所示的逆变器仿真模型进行预测误差仿真分析与计算(为了体现模型误差影响，这里不考虑延时)，仿真模型参数如表2所示。参考电流最大值为2 A。

表2 仿真参数Table 2 Simulation parameters

图2给出了电感和电阻参数不匹配时的电流预测误差仿真波形。由图2可见，当L1/L0=1.5时，电流误差Δi均值为0.14 A；当L1/L0=0.5时，电流误差Δi均值为-0.43 A。误差电流按正弦规律变化，频率与工频相等，主要与输出电流相关，与式(9)一致。参数正偏差与负偏差引起的预测误差相位相反。

图2 电感和电阻不匹配时的预测电流误差ΔiFig.2 Predicted current error Δi of inductance and resistance mismatch

在R1/R0=1.5与R1/R0=0.5时，引起的电流误差大小基本相同，最大值为0.05 A，误差相位相反。最大误差与预测电流之比为5%。在不匹配程度一致情况下，相较于电感参数不匹配，电阻参数不匹配引起的预测电流误差较小，大约为电感最大误差的30%，且基本上不存在直流分量。

图3所示为电感不匹配时的预测电流误差率|Δi/i(k+1)|仿真波形。由于相位为π及其整数倍时，预测电流i(k+1)为0，误差率趋于无穷大，图3中为进行限幅处理后波形。当L1/L0=1.5时，相位5π/6 rad处的预测电流误差率为5%；当L1/L0=0.5时，预测电流误差率为16%。

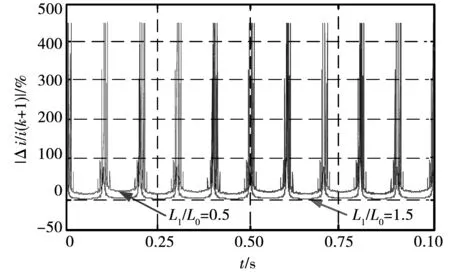
图3 电感不匹配时预测电流误差率Fig.3 Predicted current error rate of inductance mismatch

图4给出了相位5π/6rad处的预测电流误差率|Δi/i(k+1)|随参数不匹配度的变化关系。由图4可见，电感参数与电阻参数同时不匹配时，误差率更大。在L1/L0>1时，预测电流误差率随着R1增大而增大；在L1/L0<1时，预测电流误差率随着R1增大而减小。当R1/R0<1、L1/L0<1时，预测误差最大，失配情况最严重；当电感与电阻同时存在不匹配时，电感造成的误差影响更大。

图4 预测电流误差率随参数不匹配的变化关系Fig.4 Relation between predicted current error rate and parameters mismatch

图5给出了不同失配情况下的预测电流误差率与相位的变化关系。由图5可见，当相位越靠近π rad时，预测电流误差率越大。参数不匹配越严重，误差率对相位的变化越敏感。电阻参数不匹配时，预测电流误差率不受相位影响。

图5 预测电流误差与相位的关系Fig.5 Relation between current error and phase

综上可见，逆变器模型预测控制模型参数不匹配会产生电流预测误差，影响电流预测的准确性。相对而言，电感参数不匹配产生的影响比电阻不匹配大。

2 误差补偿策略

当预测模型参数与实际参数不匹配时需要进行补偿控制，以确保预测准确性以及良好的控制性能。

2.1 模型失配误差补偿策略

针对模型参数不匹配，本文提出在线RLS来实时修正模型参数。在线RLS是系统辨识中一种高效、易于在线实施的参数辨识方法，具有计算量小的优点。相对于其他参数辨识方法[18-20]，RLS算法可同时辨识电感和电阻参数，且计算速度快。辨识过程简述如下：

离散观测辨识系统可表示为

y(k)=xT(k)θ(k)+ξ(k)。

(10)

式中：y(k)为系统k时刻的观测输出；xT(k)为k时刻的输入；θ(k)为待辨识的参数；ξ(k)为噪声扰动。RLS算法辨识参数通过求解下式最小值的参数估计值来实现。

(11)

根据上述RLS算法，将式(3)表示为式(10)形式，即

i(k)=ai(k-1)+b[u(k-1)-e(k-1)]。

(12)

式中：

(13)

由式(13)可得电感和电阻参数为：

(14)

将式(12)重新表示为下列矩阵方程，即

y(k)=ΦT(k)θ(k)+ξ(k)。

(15)

式中：y(k)=i(k)；ΦT(k)=[i(k-1)u(k-1)-e(k-1)]；θ(k)=[a(k)b(k)]T为待辨识参数。

(16)

(17)

Pk+1=λ-1[Pk-Kk+1ΦT(k+1)Pk]。

(18)

式中：Kk+1为修正系数矩阵；Pk为协方差阵；初值为P0=αI，I为单位矩阵，α=104～106；λ为遗忘因子，取值范围一般为0.95～0.995。

根据辨识参数θ的值，代入式(14)可得RLS辨识出的实际电感和电阻值。需要指出的是：遗忘因子λ越大，辨识的速度越快，但是跟踪能力越差。在实际应用中需要反复试凑λ，折中考虑合适的辨识速度和跟踪准确性。

在图1所示逆变器控制系统中，利用采样i(k+1)、u(k+1)和e(k+1)和RLS辨识策略可在线辨识出电感L(k+1)和电阻R(k+1)，并实时修正MPC控制器预测模型，实现对参数误差的在线补偿，不需要额外增加传感器，成本低。

由图6可见，无论是初始0时刻初始辨识还是0.1 s时刻参数突变后的辨识，算法都能在0.02 s内实现两个参数的快速跟踪辨识，且辨识误差在5%以内。因此，RLS算法可以准确地识别出模型中的电感参数和电阻参数。

图6 逆变器参数的RLS辨识Fig.6 RLS identification of inverter parameters

2.2 改进的延时补偿策略

目前，延时补偿通常采用两步预测电流误差最小化的延迟补偿算法，即利用tk+2时刻的电流目标函数来选取最优开关状态，实现消除采样和计算延时的影响。然而，传统MPC延时补偿中，因采样频率远高于电网频率而直接将e(k+1)近似等于e(k)，这样处理会存在一定的误差[9,11]。因此，文中利用电网电压的正弦变化规律，获取k+1时刻预测电压e(k+1)补偿电网电压延时误差，即

(19)

根据式(4)可得k+2时刻的预测电流为

(20)

因此，延时补偿目标函数为

g=|[iref(k+2)-i(k+2)]|。

(21)

2.3 逆变器模型预测误差补偿策略设计

FCS-MPC误差补偿策略算法如图7所示。图中gopt、jopt和Sopt分别为最优电流目标函数、最优电压矢量标号和最优开关状态。补偿算法首先初始化R0、L0、P0、λ、K和θ(0)，然后采样k时刻输出电流i(k)和电网电压值e(k)，以及k-1时刻获取最优电压u(k)，预测电流i(k+1)和电压e(k+1)；然后，利用RLS算法获取k+1时刻的电感L(k+1)和电阻R(k+1)，并更新预测模型；进而，获取k+2时刻的预测电流，并构建预测目标函数；最后，通过寻优算法找到最优开关矢量S(k+1)，即k+1时刻的最优电压u(k+1)。

图7 误差补偿FCS-MPC算法流程图Fig.7 Flow of error compensation FCS-MPC algorithm

3 补偿策略仿真与实验

3.1 仿真结果分析

为了进行对比，进行了无延时、无失配情况下仿真，仿真结果如图8所示，图中给出了输出电流波形和电流总谐波失真(total harmonic distortion,THD)分布情况。仿真中采用延时单元模拟数据采样与计算延时，图9给出了延时0.7Ts、L1/L0=0.5、R1/R0=0.5情况下的输出电流波形和谐波分布图，其补偿后的输出电流波形和谐波分布图如图10所示。

图8 无延时与失配的输出电流性能Fig.8 Output current without delay and mismatch

由图8可见，无延时与失配情况下电流比较平滑，谐波失真THD小于0.9%。此时，谐波与毛刺主要由FCS-MPC算法仿真模型造成，如采样频率、滤波电容参数大小、模型积分步长。

对比图8、图9和图10可知，当存在0.7Ts延时、L1/L0=0.5、R1/R0=0.5情况下，输出电流波形谐波与毛刺明显增多，谐波失真THD增大到6.15%，性能明显下降。经过文中所提的补偿策略后，输出电流波形改善明显，谐波失真THD为3.30%，减少了2.85%，说明所提方法明显地改善了FCS-MPC控制效果。此外，需要说明的是模型仿真采样频率越低，补偿效果越好。

图9 延时0.7Ts、L1/L0=0.5、R1/R0=0.5时输出电流性能Fig.9 Output current of 0.7Ts delay,L1/L0=0.5 and R1/R0=0.5

图10 延时0.7Ts、L1/L0=0.5、R1/R0=0.5时误差补偿后输出电流性能Fig.10 Output current with error compensation of 0.7Ts delay,L1/L0=0.5 and R1/R0=0.5

图11给出了在L1/L0=1.5、R1/R0=0.5情况下RLS辨识补偿前后的预测电流误差对比图，图中在0.05 s前未采用RLS辨识，预测电流误差最大值为0.157 A；采用RLS辨识补偿后，预测电流误差最大值为0.001 A左右，误差幅值被减小了近千倍。因此，采用RLS在线识别参数补偿可有效地提高电流预测精度，改善逆变器控制效果。

图11 RLS补偿前后的预测电流误差对比图Fig.11 Comparison of predicted current error before and after RLS compensation

为了进一步验证文中所提补偿算法的性能，利用仿真，可得不同延时、不同失配情况下电流误差率ΔI/I、谐波失真THD值，具体如表3所示。表中ΔT为延时时间。

由表3可知，当ΔT/Ts=0.7、L1/L0=0.5、R1/R0=0.5时，电流误差率Δi/i可达20%以上，电流THD可达6.15%，说明延时与失配可严重导致性能下降。随着延时的增加，电流误差率Δi/i、系统THD都明显增加。

表3 FCS-MPC补偿性能Table 3 FCS-MPC compensation performances

经过补偿后，整体控制效果明显提升。例如：对于ΔT/Ts=0.7、L1/L0=0.5、R1/R0=0.5情况，当同时采用延时补偿与失配补偿时，电流误差率Δi/i可减少17.1%、电流THD可减少2.85%。因此，文中参数失配和延时协同补偿算法可有效地减少THD和电流误差率，改善控制性能。

3.2 实验验证

为了进一步验证所提的补偿策略，搭建了图1所示单相逆变器并网实验。实验模块采用TMS320F28335DSP板、开关管为小功率单管IGBT，型号为FGW30N60VD、二极管型号为FR307，开关频率为20 kHz，其他实验参数如表2所示。实验中，使用可变电感和可变电阻变化来模拟实际电感和电阻变化，电感和电阻初始值分别设置为10 mH和10 Ω，参数失配后的参数值为5 mH和5 Ω。

实验测试结果如图12所示，其中图12(a)为正常无失配逆变器实验结果；图12(b)为L1/L0=0.5、R1/R0=0.5时无补偿失配实验测试结果；图12(c)为补偿后的实验测试结果。由图12可见，无电感电阻失配时，输出波形平滑，THD只有1.8%；存在失配时，输出波形毛刺增多，谐波失真THD为5.4%，参数不匹配使THD增加了3.6%。采用误差补偿策略后，输出波形明显改善，电流THD为1.3%，降低了4.1%。因此，本文方法有效地提升了FCS-MPC的控制效果。

图12 实验结果Fig.12 Experimental results

图13为电感和电阻参数在线辨识实验结果。可以看出，RLS算法辨识出电感值为5.25 mH、电阻值为4.98 Ω，误差值分别为0.25 mH、0.02 Ω，准确度较高，说明RLS能有效地识别实际电感值和电阻值，可补偿参数不匹配。

图13 参数辨识实验结果Fig.13 Experimental results of identification

4 结 论

本文针对逆变器FCS-MPC参数不匹配引起的误差问题，研究了参数不匹配对误差的影响，提出了基于RLS的协同补偿方法，有效提升了控制性能。具体成果如下：

1)分析了电阻、电感失配对输出电流误差的影响及其关系，给出了误差公式；

2)建立了带遗忘因子的RLS失配参数辨识方法，提出了在线误差补偿的FCS-MPC控制算法；

3)开展了仿真与实验，验证了补偿策略有效性。所提补偿策略能同时补偿电感、电阻失配引起的性能下降，还可以补偿延时造成的误差。算法具有在线、实现简单的优点。