基于时间模糊化长短时记忆的非侵入式负荷分解方法

廖荣文，刘 刚，肖 刚

（1. 上海电力大学自动化工程学院，上海市 200090；2. 上海交通大学航空航天学院，上海市 200240）

0 引言

智能用电是智能电网的关键组成部分，能实现电网和用户的灵活互动［1］。负荷分解作为其重要的组成部分，可以为电力用户侧和供给侧政策的制定提供依据。通过了解每个家用电器的用电量，用户侧可以节省电费开支，供给侧则能提供更多的相关服务［2］。如何在较低的成本下准确分辨负荷种类并计算电能消耗，一直是负荷分解领域关注的主要问题。

近年来，基于深度学习的负荷分解方法受到越来越多的关注。文献［3-4］证明了设备中点元素的状态与中点前后的聚合电能信息相关；文献［5-7］通过同一时间点的聚合值估计特定时间点上设备的消耗，有时会对设备运行状态产生误判；文献［8］提出一种一维卷积堆叠长短时记忆循环神经网络（recurrent neural network，RNN）技术；文献［9］采用的电力特征由于依赖高频采样，所以采集设备成本较高；文献［10］基于电器的持续时间、使用时间和有功功率等非电力特征进行建模；文献［11-12］提出非传统特征与负荷分解目标值之间存在一定的相关性，但依赖于大量特征以及较多的数据。

针对以上问题，本文提出一种基于时间模糊化长短时记忆（time-fuzzified long short-term memory，TFLSTM）的非侵入式负荷分解方法，主要贡献有以下3 点：①算法的输入为有功功率，通过学习固定长度序列的映射关系来代替传统样本点的映射关系，并将数据集分割后进行单独训练，以此来提高算法准确率；②对总功率信号和设备功率信号进行建模，通过长短时记忆（long short-term memory，LSTM）建立状态点之间的联系，利用编码过程和解码过程去除非目标设备的信息，无须采集成本较高的高频特征和大量非电力特征，输入数据整体较为简洁；③引入时间模糊策略，构建了一种与时间区域相关的模糊区域规则，结合用户在不同时间区域的用电习惯实现负荷分解，以提高算法对于设备状态判断的准确率。

1 模型原理

1.1 时间分割

文献［13］提出伪卡诺图（pseudo Karnaugh mapping，PKMap）用于展示数据集中的不平衡类分布，本文引入PKMap，根据不同设备、不同时间区域的功率值给卡诺图上色，使整个数据集实现可视化，来呈现较长时间内设备使用情况的分布。本文对文献［14］房间2 的REFIT 数据集中不同时间区域的设备功率进行统计、映射和着色，并利用PKMap 排列加以呈现，从而展示不同设备的电能使用情况。每种电器单位小时内的工作状态统计如附录A 图A1 所示，图中右侧的色度图呈现了数据集采集期中可视化电功W的数量级。W的公式如下所示：

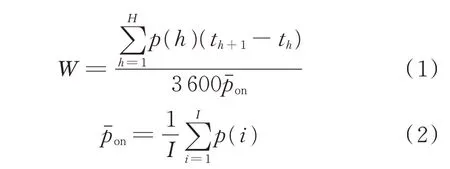
式中：I为数据集中单位小时内所有功率大于阈值功率（本文设为8 W）的采样点个数；p(i)为第i个采样点对应的有功功率；pˉon为功率均值；H为单位小时内所有采样点个数；p(h)为第h个采样点对应的有功功率；th为第h个采样点对应的时刻。通过式（1）进行处理后，可以减小所有设备W的差异，有利于标注色度图。

附录A 图A1 通过颜色深浅表示不同设备的运行时间状况，当颜色为白色时表示设备在该单元对应的时间内均处于关闭状态，其余的颜色越浅表示设备处于开启状态时间越长，颜色越深则表示设备处于关闭状态时间越长。在较长的采样时间下，大部分设备在不同时间区域的运行情况存在明显差异，某些设备在一些时间区域内基本处于不工作状态，而在另一些时间区域内则使用频率很高。根据设备在不同时间区域内的使用差异，将原始数据集划分为数据集A和数据集B。

本文统计并可视化了REFIT 数据集，所基于的数据为2013—2015 年的总表和单个设备传感器测量的有功功率数据，其中包含季节、温度、节假日与工作日等影响因素在内的所有数据。对于不同影响因素下所对应的数据，根据时间区域划分数据集并分别用于训练不同的网络，由网络分解出目标设备的功率信息，使得本文提出的算法在不同影响因素下，仍然可以保持较好的效果。同时，利用居民用电行为规律得到时间模糊策略，提高算法对于设备状态判断的准确率。

1.2 网络结构

本文提出一种长短时记忆自编码器（long shortterm memory auto-encoder，LSTMA）模型来解决负荷分解问题。首先，将输入序列的部分数据基于概率置零，保留输入序列和输出序列的差异性以更好地训练模型。经过处理后，输入序列与输出序列更加接近，提高了训练得到的权重的鲁棒性。

该方法通过学习固定长度输入和输出序列的映射关系，降低了算法误判功率值，提高了算法精度。同时，当输入信号有且仅有电表总功率信号且采样频率较低时，该网络有助于提高模型的分解能力，在负荷分解任务中相较于其他方法往往具有较好的效果。LSTMA 主要网络框架如图1 所示。

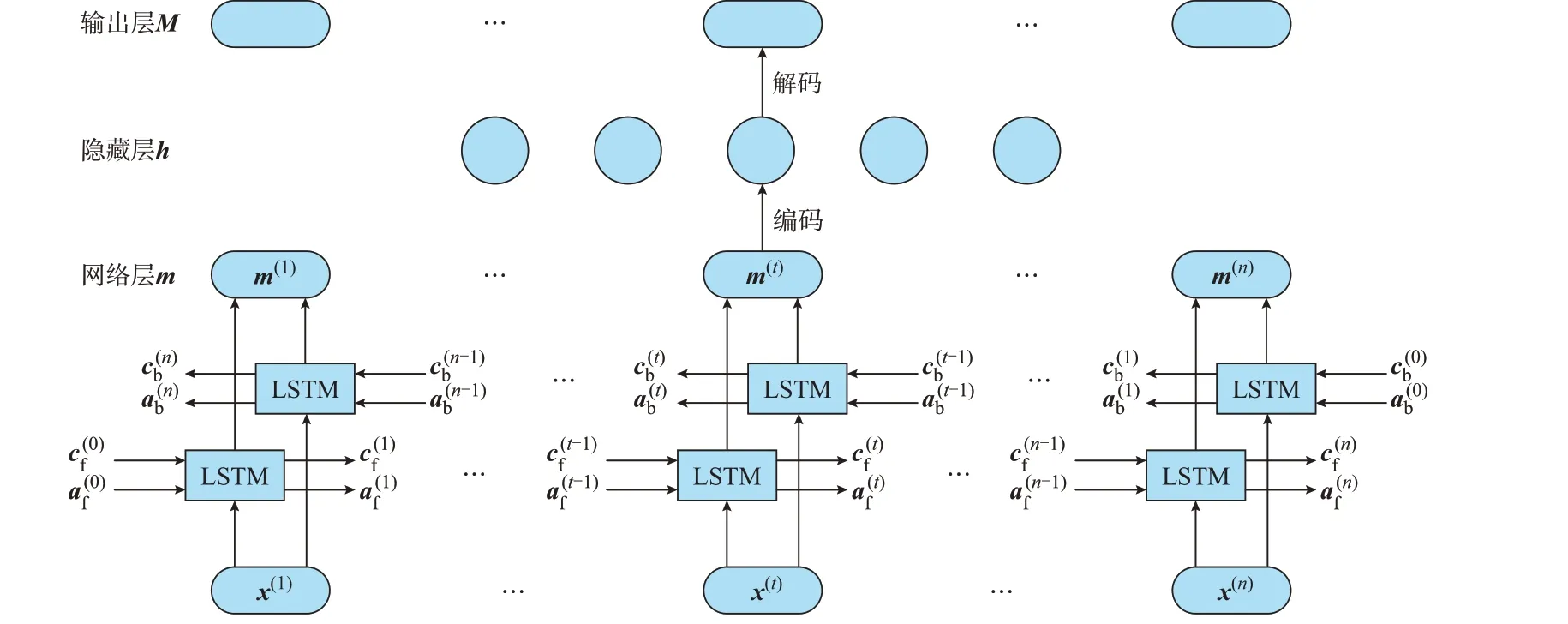
图1 LSTMA 模型结构Fig.1 Structure of LSTMA model

LSTM 网络在RNN 结构的基础上增加了记忆单元c、更新门μ、遗忘门f和输出门o，因此对于第1层正向LSTM 网络，公式如下所示：

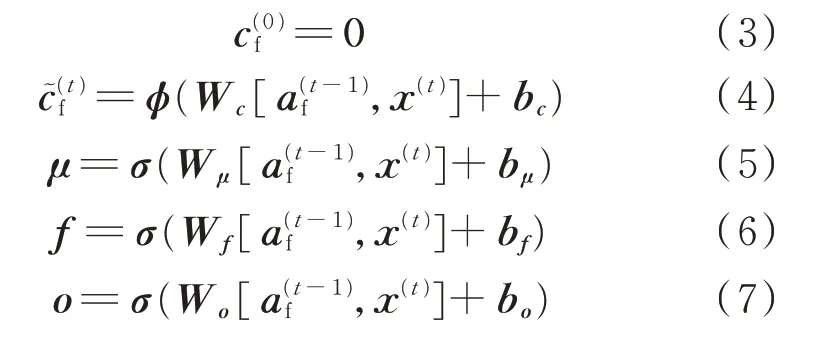
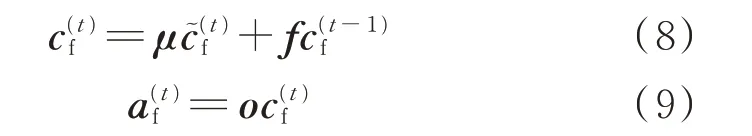
式中：记忆单元c、更新门μ、遗忘门f和输出门o对应的权重分别为Wc、Wμ、Wf、Wo，对应的偏置分别为bc、bμ、bf、bo；为记忆单元初始值；为时间步t记忆单元的状态向量，其候选值为；为时间步t非记忆单元的状态向量；x(t)为时间步t网络的输入向量；σ(·)表示sigmoid 函数变化；φ(·)表示tanh 函数变化；每个时间步更新门μ和遗忘门f共同决定是继承上一个时间步记忆单元的状态向量，还是更新为候选值。当输出门o为0 时释放记忆内容，当o不为0 时保留记忆内容。

第2 层反向LSTM 网络从与第1 层网络相反的方向训练网络参数，然后2 层网络的状态参数和组合为m(t)，网络层m经过加权映射进行数据的降维表示，得到隐藏层h，最后通过反向加权映射得到输出层M，通过上述编码过程和解码过程去除非目标设备的信息［15］。

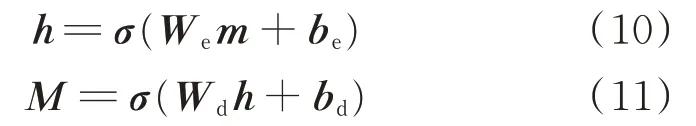
式中：We和be分别为编码层的权重和偏置；Wd和bd分别为解码层的权重和偏置。编码后提取到的m中关键信息作为后续训练网络的输入，完成从m到M的信息重构。

1.3 模糊理论与时间域模糊化

在负荷分解中，同一种家用电器在不同时间区域的使用频率会有所不同［16］，使得负荷分解和时刻呈现相关性。本文通过参考两者之间的隐含关系，提高模型对设备状态判定的准确率。

本文中论域U为24 h，即时刻点x∈[0，24)=U，fT为定义在U上的一个隶属于集合T的隶属度函数，集合T包括集合a和集合b，隶属函数fT把U中的每一个元素都映射到［0，1］区间内，代表元素隶属于T的程度，值越大表示隶属程度越高。数据集中不同时间区域信息在生成模型过程中的重要程度是不清晰的，因此根据模糊理论对论域U的模糊映射如下：

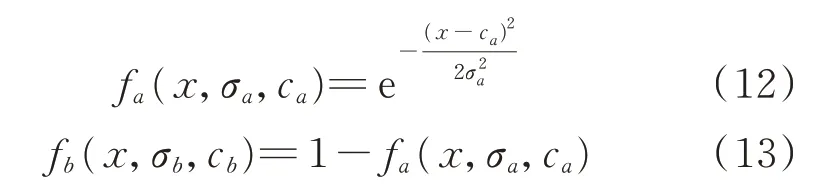
式中：fa(·)为集合a的隶属度函数，函数的均值和方差分别为σa和ca；fb(·)为集合b的隶属度函数，函数的均值和方差分别为σb和cb。

式（12）在数据层面上描述了模糊现象，体现了时间区域属性的不确定性，并通过隶属度判定时间区域的重要性。本文选用高斯型隶属度函数，隶属规则曲线如附录A 图A2 所示。图中隶属度曲线交点的横坐标即为划分数据集的时间节点。时间区域模糊化将区域模糊性转化为每个时刻对应的隶属度值，而模糊区域规则用于进行负荷分解过程中模糊区域的划分和不同时间区域信息重要性的判定。

2 基于TFLSTM 的负荷分解方法

目前，负荷分解算法基于的特征主要分为高频特征和低频特征，高频特征主要包括电压、电流和谐波信号，而低频特征则主要包括有功功率、无功功率和功率因数。然而高频特征往往依赖于高频采样，要求的数据采集设备成本较高，因此本文将有功功率作为输入，探究低频特征下的负荷分解方法。设p(tn)为在时间tn时所有家电测量的总功率。在离散时间取样下，将p(tn)简化表示为p(n)［17］，即

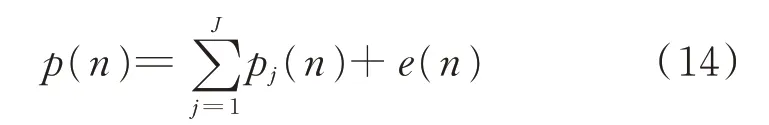
式中：J为家用电器数量；j为各类家用电器的索引；pj(n)为设备j在采样点n上的有功功率；e(n)为测量的附加噪声。

非侵入式负荷分解的目标是从已知的p(n)中提取出未知的pj(n)，而pj(n)的估算值p^j(n)与同一窗口下的总功率p(n)有关，因此可以训练一个网络来进行时间序列回归，使其可以由p(n) 得到(n)，即

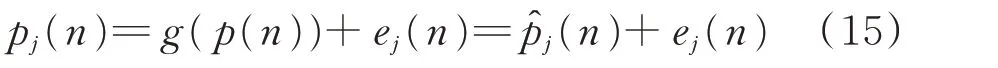
式中：g(·)为在学习过程中的非线性函数；ej(n)为测量设备j的附加噪声。

本文考虑到电力负荷与时间具有相关性，提出了基于TFLSTM 的非侵入式负荷分解方法。在式（15）的基础上，建立基于时间模糊的负荷分解函数模型：

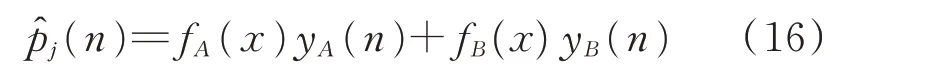
式中：yA(n)和yB(n)分别表示由数据集A和数据集B来训练模型时所得到设备j的功率估计结果；fA(x)和fB(x)为在n对应的时间点x下的模糊参数。当分割点参数确定以后，fA(x)和fB(x)就分别对应于式（13）中的fa(·)和fb(·)。TFLSTM 负荷分解方法的基本结构框架如图2 所示。

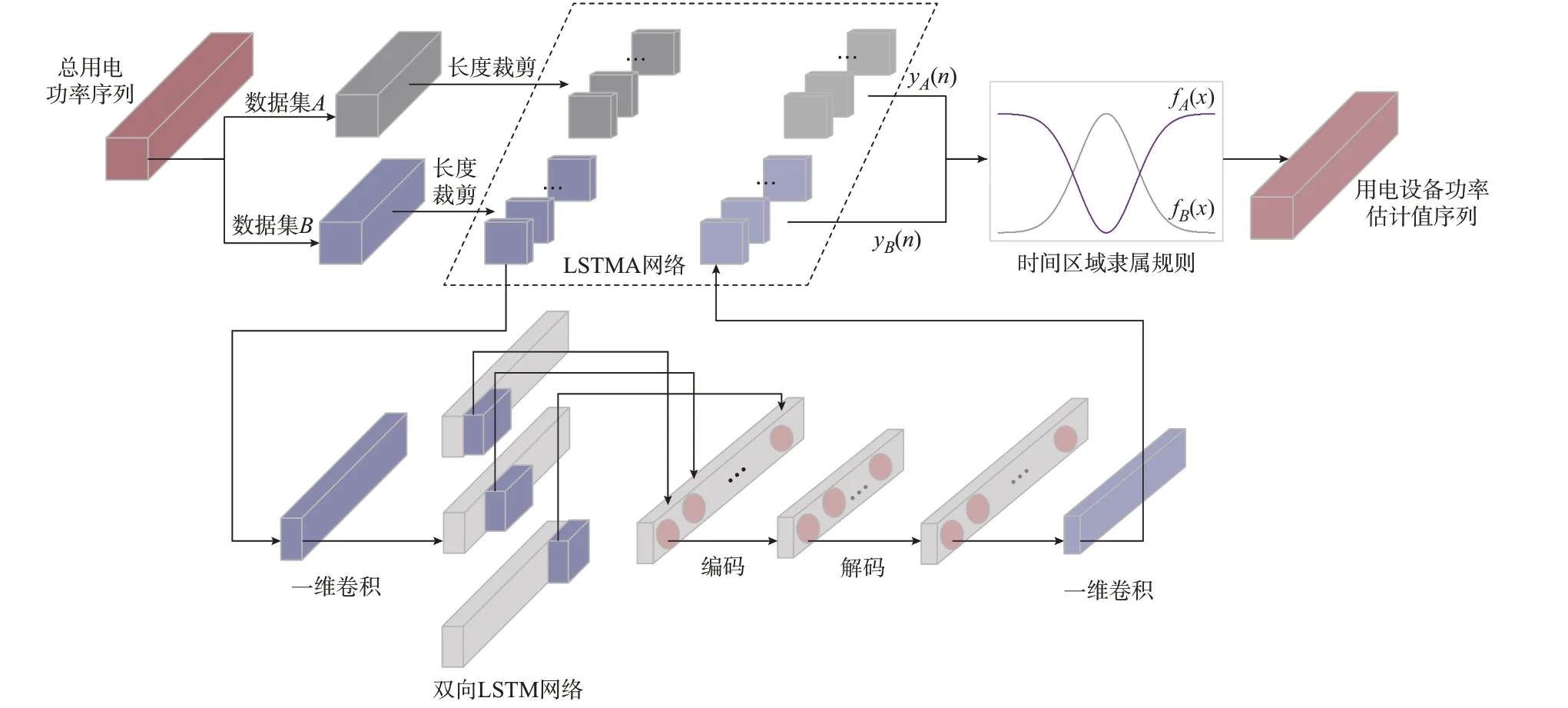
图2 算法框架Fig.2 Framework of proposed algorithm

本文所提出的负荷分解模型可以根据总用电功耗数据，分解出特定的用电设备功耗数据。通过多个不同设备的网络，即可得到多个设备的用电信息。该模型首先将原始数据集中的总用电功率序列按照时间区域分割重组，得到了2 个数据集；再根据种类不同的设备，分别将数据集裁剪成相应序列长度的集合，每小段序列经过LSTMA 网络结构，得到相应的功率估计值序列；2 个数据集共得到2 组对应设备的功率估计值序列，然后由不同时间区域对应的隶属规则，对2 组数据做进一步处理，最后输出通过分解得到的用电功耗估计值。

3 实验评价

3.1 数据集描述和参数选择

本文选用公开的REFIT［14］数据集来评价提出的算法。该数据集收集了来自英国20 户家庭2013—2015 年的总表和单个设备传感器测量的有功功率数据，在此期间，居住者照常进行工作生活任务，以确保数据中保留居住者的用电行为习惯，数据采样时间分辨率为6～8 s。保留REFIT 数据集中一周的用电数据作为测试集，其余数据用于训练，测试过程中算法辨识未知负荷的时长为9 s 左右。选择数据集中设备使用功率占比较高的几种电器作为已知电器用于验证算法，分别是：洗碗机（DW）、冰箱（FF）、水壶（K）、电视机（TV）、洗衣机（WM）。这5 种电器消耗了相当大比例的电能，而且分别代表了一系列不同电力特征的用电设备，如水壶等简单的开/关状态设备和洗衣机等复杂的多状态设备。

本文提出的TFLSTM 算法在TensorFlow2.0深度学习框架下实现，在训练深度学习模型时利用图形处理器（GPU）加速，设置采样间隔为1 min，并采用自适应矩估计（adaptive moment estimation，Adam）优化算法训练模型。每次训练迭代使用128 个样本更新模型权重和系数，将输入网络中的数据归一化到［0，1］范围内，以提高深度学习的性能。文献［3］观察到不同设备的数据在训练网络时，洗衣机等设备训练的网络可以提取比其他设备更多的信息。本文所提出的模型通过训练每个设备对应的网络来对负荷进行分类，但在实际应用场景中很难做到对每个设备单独进行网络训练，为解决成本较高的问题，选择多状态设备洗衣机作为基准设备，保留其负荷分解网络训练后得到的参数，而其他设备每次仅训练最后一层一维卷积层的相关参数。

对于一个电器设备的完整运行过程而言，稳定的区域包括具有相同特性的数据［18］。TFLSTM 算法为每个网络的输入对应设置一个样本跨度，该样本跨度下的总功率序列会通过网络得到同一时间区域下相应设备的消耗功率序列。表1 通过统计每个设备超过设定阈值功率的连续样本个数来确定样本跨度。

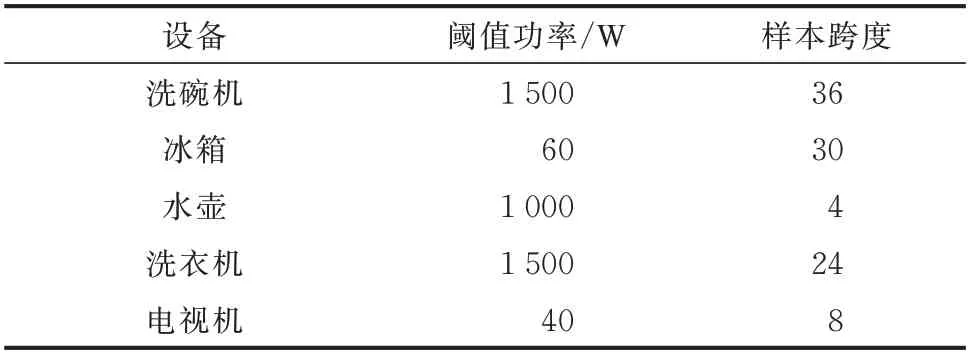
表1 样本参数选择Table 1 Sample parameter selection

3.2 评价指标

本文采用平均绝对误差（mean absolute error，MAE）、均方根误差（root mean squared error，RMSE）、归一化均方根误差（normalized root mean squared error，NRMS）、功率分解准确率cpower、召回率R和电器启动辨识准确率con作为算法的评价指标。计算公式分别如下：

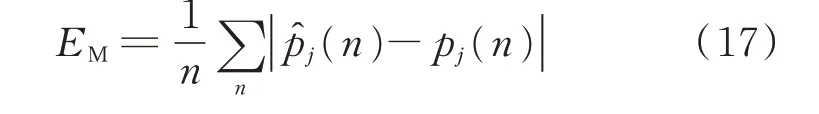
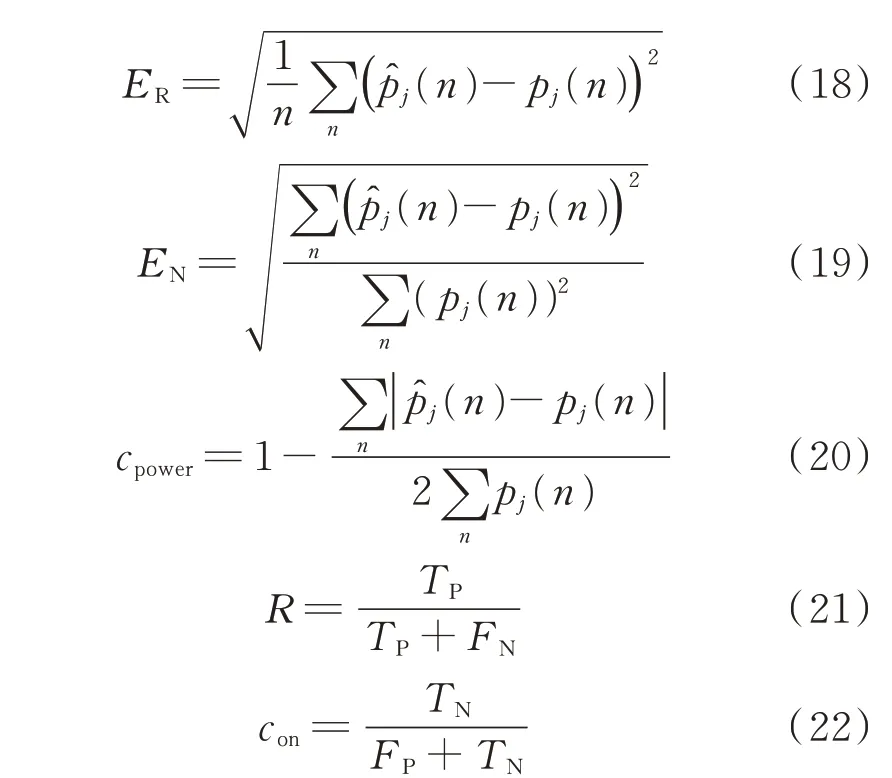
式中：EM、ER、EN分别为MAE、RMSE、NRMS 值；TP为正样本被预测为正样本的采样点总个数；FN为正样本被预测为负样本的采样点总个数；TN为负样本被预测为负样本的采样点总个数；FP为负样本被预测为正样本的采样点总个数。

3.3 数据集分割节点探究

所选数据集中包含了时刻信息、不同时刻对应的房间总有功功率数据以及测量的9 种设备各自消耗的有功功率数据。以房间2 为例，由于数据集中相邻时刻间隔的时间不等，所以本文在统计之前对数据进行了采样，采样时间为1 min，以保证每个时间区域内的采样点数保持一致，并将一个采样周期内设备所有功率值的均值作为每个采样点对应的功率值。数据集根据提供的时间信息分为00：00—01：00、01：00—02：00、…、23：00—24：00 这24 个时间区域对应的子集，剔除房间2 数据集中首尾不完整的2 d 的数据，探究了数据集不同设备在不同时间区域的用电规律。从附录A 图A3 中可以看到，除了设备1 和设备7，大部分电器在不同时间区域的使用频率存在较大差异。

根据统计的数据将时间分为06：00—18：00 和18：00—次日06：00 这2 个区域，2 个区域分别为用电设备使用的相对高频段和相对低频段，然后针对这2 个时间区域，评估训练集时间区域对分解模型测试效果的影响。房间2 的原始数据集A按照上述时间区域分成2 个数据集，其中06：00—18：00 区域的数据集记为数据集B，18：00—次日06：00 区域的数据集记为数据集C，同时2 个数据集分为训练集B1、训练集C1、测试集B2和测试集C2，并且从原始数据集中分出一个测试集A2，以LSTM 算法［19］作为用于评估的负荷分解算法。由数据集B1和数据集C1训练得到的2 个模型分别放在数据集A2、B2、C2上测试，计算3 种模型对应的ER用于评价，具体如附录A 表A1 所示。可以看出，对大部分设备而言，数据集B1训练的模型在测试集B2的效果优于测试集A2，且在测试集C2上的效果最差；数据集C1训练的模型在测试集C2的效果优于测试集A2，且在测试集B2上的效果最差，即当训练集和测试集的时间区域相同时，算法可以达到更好的分解效果。

本文提出利用粒子群优化（particle swarm optimization，PSO）算法确定时间分割节点的时间模糊策略，引入PSO 算法对分割节点x1和x2进行寻优，根据式（12）和式（13）求解模糊策略参数ca和σ2a，然后在不同时间区域训练得到的模型基础上采用模糊策略，以结合家庭用电设备的使用习惯用于负荷分解。得到不同情况下的隶属度函数后，将适应度函数值设置为EN，粒子群的数量设置为100，通过迭代筛选出最优粒子，作为最终确定的时间分割节点。附录A 图A4 展示了引入PSO 算法对分割节点x1和x2进行寻优后，5 种电器在网络迭代过程中适应度值的变化。由图可知，经过75 次迭代后，所有电器的适应度值均逐渐降低并收敛。

3.4 加入模糊的影响

在LSTM 算法和LSTMA 算法的基础上，分别加入模糊策略形成模糊长短时记忆（fuzzified long short-term memory，FLSTM）和TFLSTM 这2 种方法，表2 通过EM、ER、EN这3 种评价指标对比了4 种模型下5 种电器的非侵入式负荷监测（non-intrusive load monitoring，NILM）性能。 FLSTM 相比于LSTM，其对应的EM、ER、EN分别降低了0.44～12.46 W、4.73～56.48 W、0.04～0.17；TFLSTM 相比于LSTMA，其对应的EM、ER、EN分别降低了0.54～13.25 W、5.2～43.67 W、0.02～0.36。这些数据表明，加入模糊策略在一定程度上补偿了设备使用高频时间区域中算法对设备的分解功率，释放了设备使用低频时间区域中算法对设备的分解功率，对算法起到了一定的提升作用。

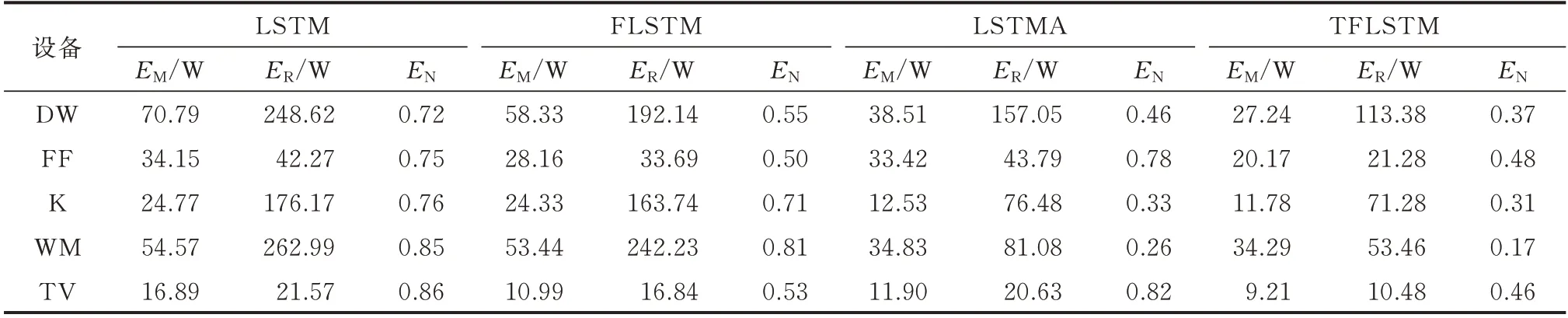
表2 加入模糊对模型的影响Table 2 Influence of adding fuzziness on the model

3.5 TFLSTM 算法与其他算法的性能对比

表 3 将 TFLSTM 算 法 与 组 合 优 化（combinatorial optimization，CO）算法［20］、因子隐马尔可夫模型（factorial hidden Markov model，FHMM）算法［21］、文献［22］中的算法进行对比。对比4 种算法下cpower、R和con指标的平均值，本文算法相较于其他算法分别高出4%～15%、0.07～0.19 和5%～13%。

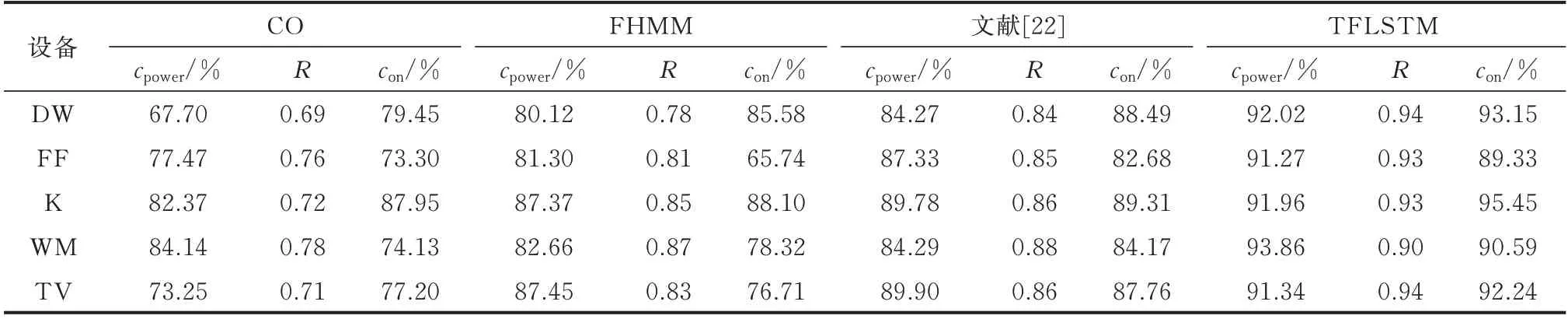
表3 不同模型的评价指标对比Table 3 Comparison of evaluation indices for different models

TFLSTM 算法引入时间分割和模糊策略，将用户的用电行为作为分解的依据之一，并改进了LSTM 算法模型，在一定程度上降低了算法对设备的误判分解功率。

3.6 复杂工况下的负荷辨识精度

在负荷分解多种实际应用场景中，总表中采集的数据往往包含大量噪声，为验证TFLSTM 在复杂工况下是否依然能够取得较好的辨识精度，本文在REFIT 数据集中加入不同分贝信噪比（signal-tonoise ratio，SNR）的高斯白噪声，即

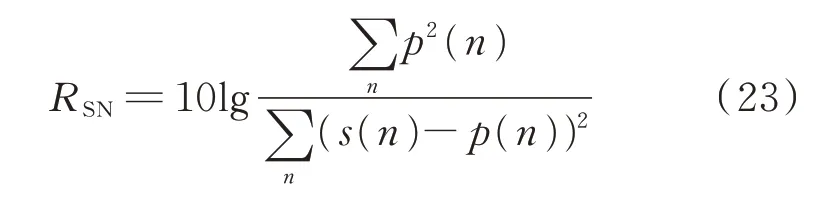
式中：RSN为信噪比；s(n)为采样点n处的噪声功率。

图3 展示了不同算法下5 种设备cpower的平均值。当噪声功率增大即信噪比降低时，算法准确率开始降低，而TFLSTM 算法和文献［22］提出的算法均在信噪比为30 dB 左右时，准确率才开始降低，并且当信噪比相同时，TFLSTM 算法的准确率均高于其他算法，因此，TFLSTM 算法在复杂工况下依然保持了较好的负荷识别精度。

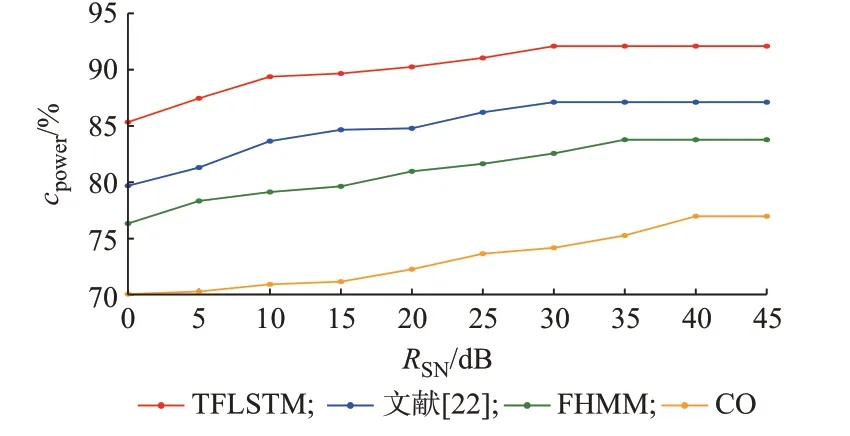
图3 不同算法的鲁棒性对比Fig.3 Comparison of robustness for different algorithms

4 结语

本文提出了一种基于时间模糊化双向LSTM的负荷分解深度学习模型，即TFLSTM 算法，可以自适应地根据设备前后的状态确定当前状态，适应设备特有的运行模式，同时通过改进的LSTM 网络分解结构，对总功率和特定设备功率在连续若干个固定长度序列进行建模。训练好的模型可以从家庭总用电数据中分解出特定电器的耗能情况，实验证明TFLSTM 算法能有效降低设备估计功率值与真实值的误差。此外，该方法中融入了时间模糊策略，将算法和用户的用电行为相结合用于负荷分解，降低了模型分解的状态误判率。未来工作将进一步研究不同地区的时间模糊策略设计方案，以期提升模型的泛化性能。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。