考虑辨识结果连续性的Type-Ⅲ型工商业负荷辨识方法

段 晶，李 勇，张振宇，李巍巍，蒋 林，李 磊

（1. 湖南大学电气与信息工程学院，湖南省长沙市 410082；2. 长沙新奥长燃能源发展有限公司，湖南省长沙市 410005；3. 利物浦大学电气工程与电子系，利物浦L69 3BX，英国；4. 长沙新奥湘江新能源发展有限公司，湖南省长沙市 410005）

0 引言

为提高电力用户终端负荷的能源利用效率、减少电量消耗、促进用户参与需求侧管理或实现远程优化控制，电力负荷的在线监测必不可少［1-2］。电力负荷的在线监测方法主要有侵入式负荷监测（ILM）和非侵入式负荷监测（NILM）两种。ILM 需要为每个监测设备配置一个或多个传感器，虽然监测结果更为准确，但成本高、配置复杂、维护困难。NILM的概念最早由Hart 于1992 年提出［3］，它只需在被监测系统的电力入口处安装一个电力信息采集装置，再通过信号分析和处理实现负荷的分解与辨识，虽然精度稍低，但是硬件结构简单，便于安装和维护，更切合智能电网建设的实际需求［4-5］。因此，近年来NILM 方法的研究备受国内外学者的关注。

负荷辨识是负荷监测的核心内容，负荷辨识方法可分为三大类：优化方法、监督学习方法和无监督学习方法。优化方法是负荷辨识最直接的方法，将提取的负荷特征数据与模板库中的特征数据进行对比，采用优化算法最小化误差，找到匹配度最高的电气设备状态组合，包括动态时间弯曲（DTW）算法［6］、遗传算法［7］、粒子群优化算法［8］等，但优化方法进行负荷辨识普遍需要根据历史信息提前建立负荷特征模板库。监督学习方法需要已知电气设备的特定运行信息进行模型的初始训练，且算法的性能很大程度取决于模型学习的数据标签，基本上是将负荷辨识问题转换为分类学习问题进行解决，主要方法包括贝叶斯分类器［9］、支持向量机（SVM）［10］和人工神经网络（ANN）［11-13］。无监督学习方法可以在没有任何先验信息的情况下运行，相较于监督学习方法减少了训练步骤的干扰性，主要算法包括隐马尔可夫模型（HMM）［14］及其扩展，如文献［15］中的因子隐马尔可夫模型（FHMM）和文献［16］中的隐式半马尔可夫模型（HSMM）均被应用到负荷辨识中。

不同类型的负荷具有不同的负荷特征，按照其运行状态可大致分为3 类［17］。对于连续变化（Type-Ⅲ）型的负荷，由于其工作状态的功率值保持连续变化的特性，导致其状态空间极其巨大。文献［18］指出，对于常用的基于HMM 的负荷辨识方法，仅对Type-Ⅰ型的开关负荷表现较好，在面对状态更为复杂的其他类型负荷时效果将被极大的削弱。因此Type-Ⅲ型负荷的辨识一直是NILM 中研究的重点和难点之一。

为有效辨识Type-Ⅲ型负荷，满足负荷辨识算法对辨识准确率和算法鲁棒性的要求，本文提出了一种基于深度卷积神经网络（CNN）和HMM 的非侵入式负荷辨识算法。通过深度CNN 提取负荷的多维特征，进行负荷的初次辨识，将连续变化的负荷状态辨识问题重构为二分类状态辨识；根据负荷状态的时间依赖性，利用HMM 解决负荷的二分类状态再辨识，减少CNN 辨识结果中出现的状态断点现象，提高辨识准确率。本文以工商业电力负荷为例，在具有代表性的Type-Ⅲ型负荷数据上进行训练和测试，证明了本文算法的有效性，并且可达到97.9%的辨识准确率。

1 负荷数据处理与特征选择

附录A 图A1 展示了3 种典型的负荷曲线，其中Type-Ⅲ型负荷的状态连续可变性特点非常明显。工商业用电在总负荷中占有很大的比重，研究工商业用电特性，对电力系统安全经济运行和电力市场的发展有着重要的作用。对工商业电力负荷进行监测和辨识，可以帮助电力部门了解客户的用电行为，进而为不同的客户群制订相应的市场策略，使双方都受益。因此，本文使用Type-Ⅲ型工商业负荷来验证非侵入式负荷辨识算法的性能。

1.1 数据处理

本文所用的数据集为实测电力数据。测量仪器为日置电能质量分析仪PQ3198，可完成无间隙的连续运算、事件检测、GPS 时间同步等标准要求的测量，测量项目包括有功功率、无功功率、频率、电压、电流及其有效值、最值和高次谐波成分等多维负荷特征数据，并具备波形记录和存储功能。在电力入口处安装数据采集装备，采样频率为1 Hz，采样时长为7 d。为了验证辨识效果，在待辨识负荷处也安装采集设备以准确获取其运行状态，从而为辨识模型提供参考数据。

对于电力入口处采集的任一负荷特征数据，可用时间序列R=[R0，R1，…，RT]表示，其中T为负荷数据的时间长度。数据处理中可通过差分的方式来增强特征的表达能力，因此可以得到负荷的差值特征序列x=[x1，x2，…，xT]，其中任一元素xt皆满足：

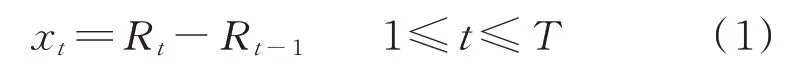
给定时间窗口长度w，并通过特征选择确定n种负荷特征，由此可生成CNN 模型能学习的输入负荷数据{H1，H2，…，HL}，其中L为输入数据的总长度。

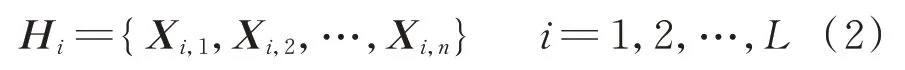
式中：Xi，j为第j种负荷特征的第i个窗口的差值时间序列，如式（3）所示。

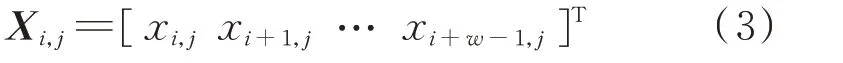
式中：i=1，2，…，T-w+1；j=1，2，…，n。

对于采集的待辨识负荷数据，以其电流有效值Ii+w/2的大小为标准，生成设备的标签状态集{y1，y2，…，yL}，其中yi为第i个时间窗口内的i+w/2 时刻点的负荷的运行状态，i=1，2，…，L。

其中，将1 A 作为状态标记的基准是根据待辨识负荷运行时的最小电流值所选择的。

1.2 特征选择

由电能质量分析仪采集的电力数据共包含3 537 种负荷特征，其中包括能反映待辨识负荷运行状态变化的相关特征和与待辨识负荷状态变化不相关的无关特征。除此之外，负荷特征中还包括一类冗余特征，即这类特征中所包含的信息可从其他特征中提取［19］。冗余特征在负荷辨识模型学习中几乎不起作用，而无关特征反而会对模型学习造成干扰。因此，在进行模型训练之前要进行特征选择，去除无关特征和冗余特征，从而提高负荷辨识的准确率，并且特征选择可以在很大程度上降低维数，减少了模型的运算量。

时间窗口长度、特征维度与CNN 的乘-加操作（multiply-accumulate operations，MAC）次数之间的关系如附录A 图A2 所示。随着特征数目的增加，神经网络的操作次数逐渐变得不可接受，另外，由于特征之间的组合状态爆炸增长，导致需要大量的数据才能对网络进行合适的训练。因此，为了降低网络运算复杂度、缩短模型训练时间，本文采用互信息算法进行特征选择。

在概率论和信息论中，2 个随机变量的互信息是变量间相互依赖性的量度，互信息熵越大表明2 个随机变量之间的相关性越强，反之互信息熵越小，2 个随机变量之间的相关性就越弱［20］。互信息值I(x，y)的计算如下：

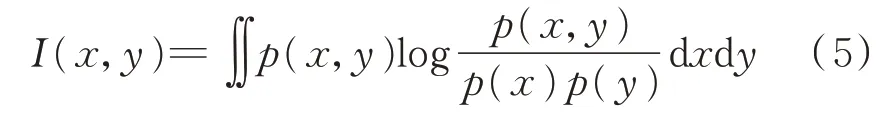
式中：p(x)和p(y)分别为随机变量x和y的边缘概率密度函数；p(x，y)为x和y的联合概率密度函数。

本文采用互信息进行特征选择的具体步骤为：根据式（5）计算每个负荷特征与待辨识负荷运行状态之间的互信息值；按照互信息的大小对所有特征按从大到小进行排序；然后选择前n个互信息最大的特征，构成负荷辨识的初始特征集合{f1，f2，…，fn}；计算fi与fj(i＜j)之间的互信息大小，若fi与某个特征fj的互信息值大于阈值，则将fj移除特征子集，并按照顺序添加新的特征；重新计算新的特征子集中特征之间的互信息值，重复筛选直到两两特征之间的互信息值皆小于阈值，并构建新的特征集合。

附录A 图A3 以热图的形式展示了负荷特征之间的相关性。图A3（a）中互信息值很小，不同特征之间的相关性很弱，而图A3（b）则相反，说明不同负荷特征之间存在冗余性，特征提取时可从不同的特征中提取重叠的信息，以致于增加了许多不必要的运算。因此，去除冗余特征可使得模型在相同的运算维度内，提取到更多的隐含特征。

2 深度CNN-HMM 负荷辨识算法原理

对于Type-Ⅲ型负荷，本文引入了具备强特征提取能力的CNN 模型，用于提取连续的负荷功率变化中隐含的特征。但是，纯CNN 类的方法具有另一种弊端，在本文中将其表述为辨识结果的非连续性问题，如附录A 图A4 所示。由于CNN 本身不具备时序建模能力，所以其对时序数据的感知范围仅能停留在所选取的时间窗长度内，这导致CNN 的辨识结果中经常出现局部性的辨识错误。值得注意的是，使用CNN 重新提取负荷数据中的特征并将其重构为运行或非运行的二分类状态，可以解决HMM面临的状态空间过大的问题，使其重新适用于HMM 对负荷状态的表达。因此，本文最终确立了使用CNN-HMM 架构的Type-Ⅲ型负荷运行状态辨识的解决方案。

2.1 算法流程

基于深度CNN-HMM 的非侵入式负荷辨识算法流程如图1 所示。

图1 基于深度CNN-HMM 的负荷辨识算法流程图Fig.1 Flow chart of load identification algorithm based on deep CNN-HMM

第1 阶段为数据处理：采用互信息算法对电力入口处采集的高维负荷数据进行特征选择，并采用差分处理的方式强化特征表达能力；对于待辨识负荷数据，根据电流有效值大小确定其运行状态，生成设备的标签数据集。

第2 阶段为模型训练：将负荷特征数据和标签数据合成模型的训练数据集，训练深度CNN，使其学习拟合特征数据与标签之间的非线性映射关系；通过深度CNN 得到负荷的初始辨识结果，并将其作为HMM 的已知观测序列，训练HMM 的参数。

第3 阶段为模型评估：将负荷特征数据和标签数据合成模型的测试数据集，采用深度CNN 模型提取负荷的隐含特征并进行初次辨识，然后采用HMM 优化CNN 辨识结果中的状态断点问题，由此得到负荷的最终状态序列，并根据负荷标签数据对CNN-HMM 辨识结果的准确率进行评估。

2.2 深度CNN 结构

残差神经网络（ResNet）因其特殊的捷径连接结构，不仅能通过增加网络的深度来提高准确率，而且可缓解由深度增加所带来的梯度消失问题［21-22］。因此，本文采用ResNet-50 网络作为深度CNN 的基本架构，通过ResNet-50 的学习，逐渐增加输入特征向量的深度，减小其数据维度，提取数据的深层隐含特征，由此优化神经网络的学习性能。附录A 表A1为ResNet-50 网络结构的超参数。

2.3 HMM 参数计算

HMM 是关于时间序列的概率模型，可用一个五元组参数λ={U，V，A，B，π}来表示，其参数定义如下。

1）U={u1，u2，…，uN}是一组隐含状态的集合，其中N为隐含状态数目，系统在t时刻的隐含状态Qt∈U。本文采用CNN 进行负荷特征提取，并将其重构为二分类状态负荷辨识问题，所以本文实验所选择的待辨识负荷的隐含状态数目N=2，只有工作状态和非工作状态，即U={0，1}。

2）V={v1，v2，…，vM}是一组观测状态的集合，其中M为每一个隐含状态可能输出的不同观测值的数目，系统在t时刻的观测值St∈V。对于待辨识负荷，观测状态数目M=2，即V={0，1}。

3）状态转移概率矩阵A=(aij)，其中aij为在t时刻状态为ui的条件下，在t+1 时刻状态为uj的概率，计算公式如下。

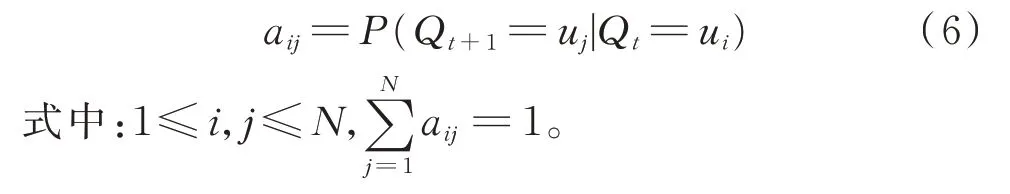
4）观测状态转移概率矩阵B=(bi(k))，其中bi(k)为在t时刻隐含状态为ui的条件下，观测状态为vk的概率。

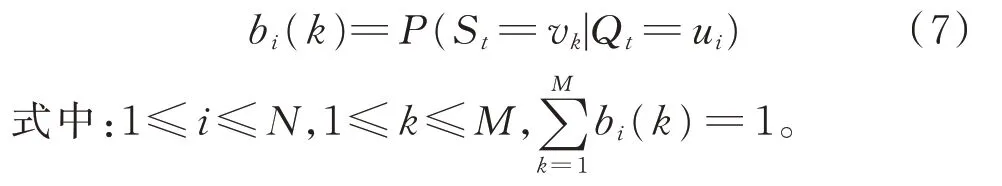
5）初始状态概率矩阵π=(πi)为t=1 时刻初始状态的概率分布。

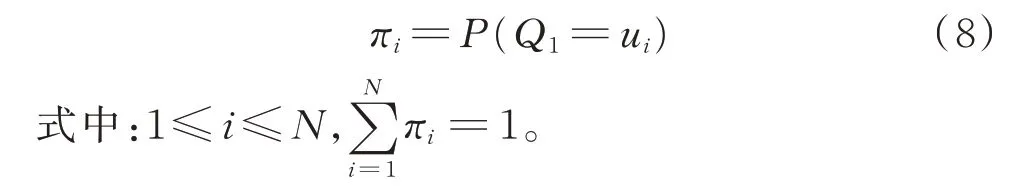
本文提出的非侵入式负荷辨识算法采用ResNet-50 模型对负荷数据进行初辨识，并将其重构为运行或非运行的二分类问题，再采用HMM 对初始辨识结果进行优化。HMM 算法的具体步骤为：①初始化HMM 可更新参数λ′0={A，B，π}；②根据深度CNN 的初辨识结果生成观测序列S=[S1，S2，…，SL]；③迭代更新的参数λ′，直到观测序列出现的概率P(S|λ′)达最大值；④通过最优参数λ′和观测序列S，采用维特比算法求使得可能性P(Q|S，λ′)最大的状态序列Q=[Q1，Q2，…，QL]，即为待辨识负荷的最终辨识结果。

3 算例分析

3.1 评价指标

负荷辨识算法的性能可用准确率Acc、精确度P′、召回率R以及调和平均评价指标Fscore进行评估。准确率Acc的计算如下：

式中：m为经过算法辨识预测正确的数量。

精确度P′用来表示算法抗误检的能力，召回率R用来表示算法抗漏检的能力。

式中：TP为被辨识为正样本、实际为正样本的数量；FP为被辨识为正样本、实际为负样本的数量；FN为被辨识为负样本、实际为正样本的数量。

Fscore是用来平衡精确度和召回率的评价指标。

此外，本文采用Wasserstein 距离衡量负荷辨识结果的运行时间概率分布与实际负荷运行时间概率分布之间的差异［23］，距离可表征算法解决识别错误断点的能力，该值越小表明2 个概率分布之间的拟合程度越好。Wasserstein 距离的计算公式如下。

式中：pr和pg为需要计算二者之间距离的2 个概率分布；inf(·)表示取最小值；Π(pr，pg)为以pr和pg为边缘分布的所有可能的联合概率分布γ的集合。从γ中采样(x，y)～γ，计算其范数距离||x-y||，由此计算该联合分布下的距离期望值E(x，y)～γ(||x-y||)，所有可能的联合分布中取该期望值的下确界为Wasserstein 距离。

3.2 算例数据集介绍

本文实验所用数据集为实测电力数据，数据采集地点分别为湖南大学研究生教学楼和湘江欢乐城能源站。其中，教学楼背景负荷较为简单，主要用能设备包括电梯与中央空调。而能源站用能结构较为复杂，它是一个冷热电综合能源站，包括溴化锂机组、蒸汽锅炉、燃气热水锅炉、热水锅炉循环泵等多种用能设备以及内燃发电机等发电设备。除去大型设备外，也存在数量众多的中小型负荷，由于供能覆盖范围较大，难以穷举。为满足2 所酒店与冰雪世界的用能需求，设备机组经常处于复杂的动态调控过程中，用电情况多变、辨识难度较高，是一个典型的工商业复杂负荷。

附录A 图A5 为实验数据采集地点的电网拓扑结构图，数据采集装置的安装位置已在图中标记。图A5（a）为教学楼低压侧的拓扑，包括相互独立的1 号与2 号电梯、中央空调、照明设备等，本文选择1 号电梯负荷为待辨识负荷，采集的部分电梯负荷数据见附录B。图A5（b）为能源站低压侧的拓扑与其部分负荷，为保障能源站供电的安全可靠性，其中包含两支独立的进线，电源进线为消防负荷供电，非消防负荷进线为其他电力负荷供电，本文选择锅炉负荷作为待辨识负荷。

图2 为待辨识负荷的有功功率和无功功率的联合分布图。可以看出，电梯负荷和锅炉负荷的有功和无功功率变化范围都非常广泛，并且分布较随机，不能简单地将其聚类处理划分为有限个状态，且其有功功率并非维持在一个或多个稳定值附近。电梯负荷和锅炉负荷的状态多变复杂，是典型的Type-Ⅲ型负荷，因此可以作为验证本文算法有效性的待辨识负荷。

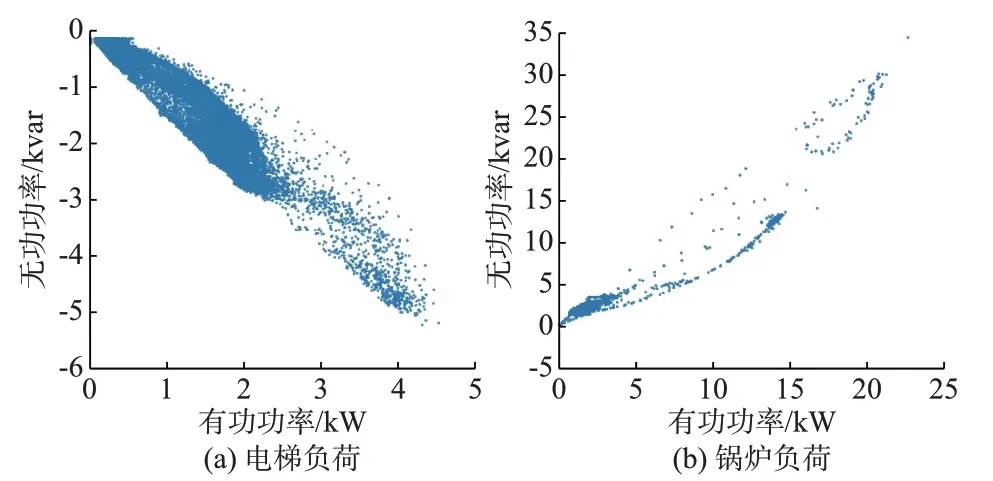
图2 待辨识负荷的有功、无功功率联合分布图Fig.2 Diagrams of active and reactive power joint distribution for load to be identified

3.3 时间窗口长度和特征数目对负荷辨识的影响

对采集的数据集进行预处理和特征选择时，选择不同的时间窗口长度w和特征数量n会产生不同的辨识结果。表1 为固定w=50 s 时，不同的特征数目对ResNet-50 网络每轮训练时间的影响。由表1 可知，随着特征数目的增加，输入数据维度变大，网络的训练时间也会随之变长，因此采用互信息进行特征选择可以缩短模型的训练时间，从而提高模型运算效率。

表1 ResNet-50 网络每轮的训练时间Table 1 Training time of each epoch in ResNet-50 network

图3 展示了算法辨识准确率与时间长度和特征数目的关系。由图可见，随着n的增加，负荷辨识模型可从输入数据中提取更多的隐含特征，但当n达到某一数值后，选择的负荷特征中开始出现重叠信息或是无关信息，反而会对模型辨识产生干扰，降低辨识的准确率；随着w的增加，模型可从一个时间窗口内学习待辨识负荷状态之间的时间连续性，从而减少辨识结果非连续性的现象，但当w覆盖负荷的最大运行周期值时，模型逐渐达到饱和，负荷辨识准确率便不会随着w的增大而增大。综合考虑算法的运算量和准确率，本文选择时间窗口长度w=60 s、特征数量n=40 进行特征选择和模型训练。

图3 时间长度和特征数量与辨识准确率的关系Fig.3 Relationship of time length, number of characteristics and identification accuracy

3.4 ResNet-50 网络训练过程

从实验数据集中选择周六的数据作为网络的训练数据，选择周一的数据作为测试数据，并且在训练数据中将80%用于训练，其余20%用于模型的评估，从而选择出效果最佳的模型。在训练过程中，采用Adam 优化器，设置初始学习率为0.001，并使用线性整流函数(ReLu）以加快模型的收敛速度，用交叉熵函数计算分类误差。附录A 图A6 为损失函数值随训练过程迭代次数的变化曲线图。可以看出，在迭代次数达到30 左右时，无论是训练误差还是评估误差，模型的损失值都趋于平缓，达到收敛状态。

3.5 与其他辨识算法的对比

本文将几种常用的非侵入式负荷辨识算法作为对比算法进行测试，包括k最近邻(KNN）［24］、随机森林（RF）［25］、HMM［14］、长短期记忆（LSTM）网络［12］、CNN［11］以及CNN-LSTM 模型。其中，选择HMM和CNN 算法是为了对比本文算法相较于单独模型的优化效果。KNN 和RF 算法是经典的分类识别算法，而LSTM 网络模型是处理时间序列的神经网络，这3 种算法均被普遍应用于非侵入式负荷辨识领域中。

待辨识负荷的辨识结果如表2 所示，图4 展示了几种负荷辨识算法在相同时间内的辨识结果。由图4 可见，LSTM 和CNN 算法的辨识结果中都存在一定的状态断点问题，导致负荷辨识的准确率降低；而2 层模型CNN-LSTM 和CNN-HMM 相较于单独模型在一定程度上优化了辨识结果的非连续性，提高了负荷辨识的准确率，且HMM 比LSTM 的优化效果更为显著，本文提出的CNN-HMM 算法具有更高的精度。结合表2 中的评价指标对比，可在数据上证实这一观点。虽然在精确度P′和召回率R上，本文算法并非是最优的，即本文算法在所有对比算法中并不具有最强的抗误检和抗漏检的能力，但是对于能综合反映辨识结果的可靠程度指标Fscore，提出的算法取得了0.987 9 的最高值；对于反映负荷辨识结果与实际运行状态之间差异的Wasserstein 距离，提出的算法取得了最小值，而d值越小表明算法解决识别错误断点的能力越强。综上所述，本文算法对于Type-Ⅲ型工商业负荷的辨识效果优于其他对比算法，并且具有最高的辨识准确率，能达到97.9%。

表2 待辨识负荷的辨识结果Table 2 Identification results of load to be identified

图4 辨识结果对比Fig.4 Comparison of identification results

3.6 用户用电行为分析

用户的用电行为是指在什么时间用了什么电器产生了多大的负荷，通过NILM 技术可以方便地获得各电器的使用情况，进而可以对各电器的用电信息如启停时间、持续时间及用电量等进行统计，以得到用户准确的用电行为，从而帮助电网公司制定供需互动策略。

附录A 图A7 为根据负荷辨识结果得到的电梯负荷和锅炉负荷一天的用能统计。由图A7（a）可知，电梯负荷的运行具有明显的时间特性，主要用电行为集中在09：00—23：00，而在00：00—06：00 时段内几乎没有运作，且工作日的运行时长较周末的略长，这与电梯负荷所处的学校环境有关，电梯的运行时段与学生上下课时段重合。由图A7（b）可知，锅炉负荷的运行几乎与时间无关，因其处于供能站内，要满足站内所有的供热需求，所以锅炉负荷每天的工作时间都很长，用能量很大，且工作日与周末的用能并没有很大区别。

4 结语

为有效辨识Type-Ⅲ型负荷，本文提出了基于深度CNN-HMM 的非侵入式负荷辨识算法。首先，根据互信息原理进行特征选择并去除冗余特征，采用参数搜索确定最优时间窗口长度和特征数目；由于ResNet-50 网络可有效解决深度网络训练过程中梯度消失的问题，将其作为深度CNN 模型的架构，提取负荷的多维特征，并完成初次辨识；根据初次辨识结果，计算HMM 的参数，并完成负荷的二次辨识，从而优化CNN 模型辨识中存在的辨识结果非连续性问题；最后，与其他负荷辨识算法的对比测试结果表明，本文算法能有效辨识Type-Ⅲ型工商业电力负荷，具有更好的准确率和辨识精度。

下一步的工作重点是研究Type-Ⅲ型负荷运行时的典型状态辨识问题。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。