集成经验模态分解与深度学习的用户侧净负荷预测算法
刘友波,吴 浩,刘挺坚,杨智宇,刘俊勇,李秋航
(1. 四川大学电气工程学院,四川省成都市 610065;2. 国网成都供电公司,四川省成都市 610041)
0 引言
负荷预测是电力系统安全经济运行与稳定发展的重要内容,其与电网的发展规划、电力市场的运行、电力调度紧密相关[1]。近年来,许多机器学习算法被应用于负荷预测。文献[2]采用协整-格兰杰因果检验分析用电量与长期经济趋势、循环分量以及季节分量之间的关系,减小了支持向量机对数据长度、质量的依赖,从而改善了预测效果。文献[3]提出了一种核函数极限学习机模型并应用于小容量微电网的短期负荷预测。随着深度学习技术的兴起,如深度置信网络[4]、循环神经网络[5-6]、生成对抗网络[7]已应用于负荷预测并取得一定的成果。文献[8]则利用长短期记忆(LSTM)网络和轻梯度提升机进行短期负荷组合预测,可降低单一模型机端预测误差的风险,提高预测精度。上述方法都是通过数据拟合各因素和电力负荷的影响关系,直接预测负荷净需求。然而,随着用户侧分布式能源尤其是园区内、表计后新能源的装机容量增长,用户端口的净负荷需求呈现出强随机性和波动性,给主动配电网净负荷预测带来挑战,成为当前研究的重点与难点[9]。
用户侧净负荷分离属于一种单通道盲源分离(single channel blind source separation,SCBSS)问题,即传感器接收到一组信号的混合数据,研究人员期望将原始信号一一分离出来。如果在某些域中存在足够大的差异,如时域、频域、联合域和其他变换域,则可以进行信号分离。基于此共识,文献[10]通过变换域滤波实现了信号识别。此外,文献[11]总结了一些通用的SCBSS 方案。目前大多数基于连续小波变换[12-13]的研究取得了不错的效果,是时频分析中常用的数据处理工具,但是这种方法需要事先指定基函数并逐一进行尺度搜索,计算冗余、计算量大,不具备自适应性。而经验模态分解(EMD)无须预先设定任何基函数,依据原始时序数列自身特点从数据层面进行SCBSS。因此,理论上EMD 可以处理任何类型的时间序列[14-15]。在针对用户侧净负荷等非平稳数据的处理上,数据分解是基于数据信号序列的各个时间尺度的局部特性。因此,其具有自适应性和优越性。文献[16-17]介绍了EMD 算法在负荷预测中的简单应用。自适应噪声的完全集成EMD(complete ensemble EMD with adaptive noise,CEEMDAN)作为一种改进的EMD 算法,可以实现可忽略的重建误差,并解决信号加噪声的不同实现方式的“模式混合”问题[18],突出展示各频率负荷特性,从而构建不同频率下的负荷预测模型,精准刻画用户侧净负荷需求。
端口表计只可测量园区的综合净负荷需求,电网公司难以获取用户侧负荷、风光分布式能源各分量的数据信息,这是传统预测方法的关键难点。因此,本文以盲源分离独立预测的思路来研究含分布式电源智能园区的净负荷需求预测问题,采用CEEMDAN 方法对具有不同变化特征的信号进行时序分解,配合深度信念网络(deep belief network,DBN)独立预测,实现用户侧净负荷一次性精准预测,可以有效避免进行单独预测产生的预测误差累积,减少调度中心预测系统的配置成本。
1 时序数列的EMD 算法
1.1 净负荷需求
随着分布式能源的发展与智能电网的进步,电网将会朝着各个智能化单元的方向发展,对于一个智能台区中既含有风能又含有太阳能的系统,除开自身运行所需的电量外,其可向整个大电网提供的电量或其所需大电网供给的电量将是智能电网负荷预测所要考虑的一个重要指标。这种“净负荷”指标的获得依赖于给智能园区风力发电功率、光伏发电功率、负荷功率带来波动后,进行更加准确的预测。
净负荷需求主要包含3 个部分。在一个研究区域的原始负荷基础上减去光伏、风机等所有形式的分布式能源出力后,即可得到本文所研究对象的净负荷需求。风机和光伏出力的不确定性给净负荷需求预测带来了极大的挑战。由于新能源的出力,光伏和风机往往就地平衡了一些原始负荷,使得净负荷发生波动性变化,而电网运营公司只关注于用户从电网获得的电能,即净负荷。
1.2 传统EMD
EMD 由黄锷等人提出,用于分析处理波动性较大的非平稳非线性信号[19]。它可以将任何信号分解为若干个本征模态函数(intrinsic mode function,IMF),每个IMF 代表着不同的振荡成分,所生成的IMF 应满足以下2 个要求。
1)IMF 极值的数量与穿越零值的次数必须相等或最多相差1。
2)在IMF 的任意一点,由局部最大值定义所形成的上包络线的平均值和局部最小值定义所形成的下包络线的平均值应等于零。其分解流程如图1 所示,步骤如下。

图1 EMD 流程图Fig.1 Flow chart of EMD
步骤1:获取净负荷需求数据P(t),通过局部最大值和局部最小值的3 次样条插值来创建其上包络和下包络线。
步骤2:计算上下包络线的平均值m(t)。
步骤3:在原始净负荷需求数据P(t)中减去m(t),检验剩余部分h(t)是否满足之前所述的IMF的2 个要求,如果满足则h(t)为其中一个IMF 分量,记为Ii(t),如果不满足则将h(t)作为新的输入重复步骤1 至步骤3,直至满足要求。
步骤4:将所有IMF 从P(t)中分离出来,令IMF总个数为N,得到N个IMF 分量Ii(t),其中,i=1,2,…,N。检验残余序列Res(t),停止条件为残余序列是否为常数或单调函数,如果不满足则继续寻找IMF,如果满足则停止分解,最终的净负荷信号分解结果如式(1)所示。

1.3 CEEMDAN
CEEMDAN 方法通过添加自适应白噪声以及计算独特信号残差来克服EMD 的不足,从而获得IMF,使重建后的信号几乎与原始信号相同。CEEMDAN 方法不仅克服了现有的EMD 模式混合现象,而且通过增加分解次数减少了重构误差。
定义Ej(·)为通过EMD 获得的第j个模式分量的计算算子,则待分解的原始净负荷曲线P(t)经过CEEMDAN 的第k个IMF 为Iˉk,其算法步骤如下。
步骤1:CEEMDAN 采用原始净负荷曲线P(t)+ε0ωi(t)在第1 阶段(k=1)时进行M次实验,其中ωi(t)为符合正态分布的高斯白噪声,i=1,2,…,M,ε0为高斯白噪声幅值常数。通过EMD对其进行分解,来获取第1 个本征模态函数Ii,1,则CEEMDAN 得到的一个分量Iˉ1为M次实验所有Ii,1的均值,即

步骤2:在第1 阶段,计算第1 次的残余序列r1(t)。

步骤3:对序列r1(t)+ε1E1(ωi(t))进行M次EMD,直到获得其第1 个IMF,其中ε1为第1 阶段后添加的高斯白噪声自适应系数,E1(·)为EMD 得到的第1 个分量。此时,可以计算得到CEEMDAN 的第2 个分量。

步骤4:对于其余每个阶段k,需要重复步骤3,并按以下方式计算k+1 模态分量。

式中:rk(t)为第k次的残差序列;εk为第k阶段后添加的高斯白噪声对应自适应系数;Ek(·)为由EMD得到的第k个分量。
步骤5:执行步骤4 直至获得的残差信号不再执行任何IMF,且标准条件是无法从残差中提取IMF,极端点的数量不超过2。
最终残差信号为:

式中:K为模态分量的总数。
因此,原始净负荷信号序列P(t) 经过CEEMDAN 最终分解为:

CEEMDAN 方法通过添加标准正态分布的白噪声可以解决传统的EMD 模态混叠问题,在电力用户侧净负荷信号分解上更具备自适应性[20-21]。
2 用户侧净负荷预测模型
2.1 受限玻尔兹曼机
玻尔兹曼机由Hinton 和Sejnowski 于1986 年首次提出[22]。后来,Smolensky 提出了一种改进的玻尔兹曼机,也称为受限玻尔兹曼机(restricted Boltzmann machine,RBM)。RBM 是一种能量生成模型,通常由2 层组成,即可见层和隐藏层,层间全连接。RBM 的体系结构如附录A 图A1 所示。
在图A1 中,可见层V用于输入训练数据,而隐藏层H包含特征检测器。第σ个可见和隐藏单元分别用vσ和hσ表示,每一层可见单元数量和隐藏单元数量分别用nv和nh表示,aσ和bσ为偏差。同一层的各个单元之间没有连接,但是每个单元仍然通过对称权重矩阵W与另一层的单元完全连接。可见和隐藏单元的能量表示为:式中:wστ为可见层第σ个单元vσ与隐藏层第τ个单元hτ之间的权重参数。
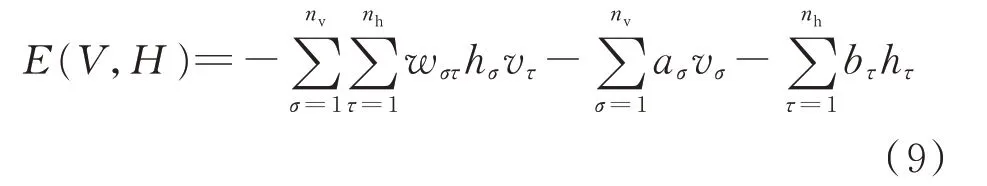
可见层的概率分布函数为:

为了学习RBM 权重参数w、可见层偏置参数a、隐藏层偏置参数b的集合θ={w,a,b}的值,需要把方程式给出的似然函数最大化。似然函数形式定义为L=lnp(V),因此梯度为:

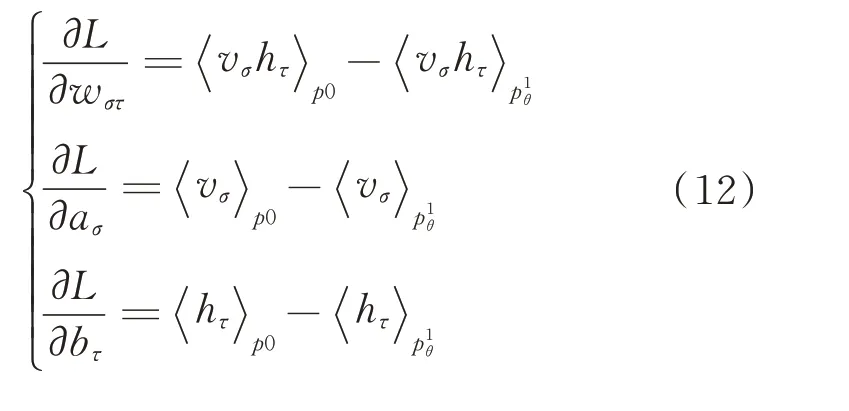
2.2 DBN
DBN[23]是一种导入的深度学习模型,而RBM是其基本模型之一,DBN 通过若干层RBM 堆叠后加一层反向传播(back-propagation,BP)神经网络构成,其架构和训练过程如附录A 图A2 所示。图中所示的DBN 是通过堆叠若干个RBM 形成的。它的训练过程分为2 个步骤:无监督训练和微调。在步骤1 即无监督训练期间,使用CD 算法以能量函数最低来训练第1 个RBM。得到第1 个训练完成的RBM 后,其隐藏层用作第2 层RBM 的可见层,以训练第2 个RBM,以此类推直至所有的RBM 全部训练完成。步骤2 使用从步骤1 获得的参数作为初始值,通过BP 对DBN 进行微调。值得注意的是,通过使用从步骤1 获得的参数初始化网络而不是随机初始化,可以避免训练过程中的局部最优。
3 某地区实际数据算例测试
为解决电表后分布式能源不可观带来的用户侧净负荷难以精准预测问题,本文提出基于CEEMDAN-DBN 的电力用户侧净负荷需求预测框架模型,如图2 所示。

图2 净负荷需求预测框架模型Fig.2 Framework model of net load demand forecasting
首先获取原始净负荷数据信号,通过CEEMDAN 得到若干个IMF 分量及残差分量r。之后引入电力用户当地的气象数据,包括光照、温度、风速等,这些因素关系到用户电表后的光伏发电出力、风机发电出力和负荷数据,对净负荷有至关重要的影响,通过气象数据与净负荷数据构成训练集合,针对每个IMF 分量独立并行训练DBN 模型,得到各自最佳预测模型。最后,通过测试集验证,将所有DBN 的输出结果相加得到最终的用户净负荷预测结果。为了验证本文所提方法的优越性和有效性,采用某地区实际净负荷数据(该地区含有大量光伏发电与风机发电装置,波动性清洁能源占比高)叠加到负荷数据上,导致净负荷需求不平稳性增强,体现了本文所提方法在非平稳时序数列上预测的优势。
3.1 CEEMDAN 算例
为了比较净负荷需求信号的EMD 和CEEMDAN 的分解效果,选择504 个用户侧负荷时序数据点进行分析,分解效果如图3 和图4 所示。根据CEEMDAN 的建议,ε0和M是非常重要的参数。ε0的合适值在0.01 至0.5 间,而较大的M会延长算法的运行时间。考虑到实际的计算条件,选择ε0=0.2 和M=500。同时,EMD 和CEEMDAN 算法分解负荷曲线所用时间分别为0.665 s 和6.472 s,均满足小时级尺度的短期负荷预测要求。

图3 EMD 结果Fig.3 EMD results
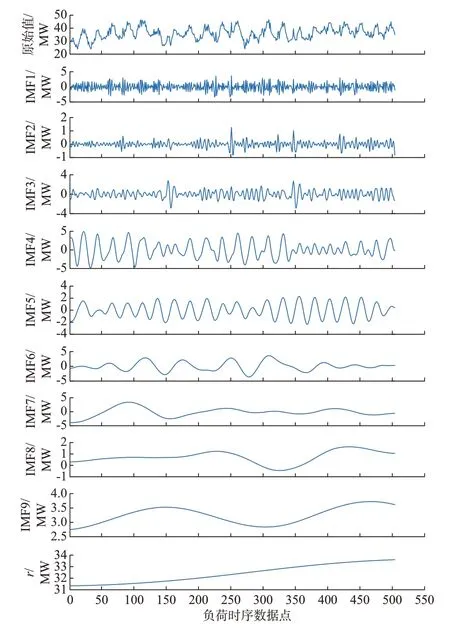
图4 CEEMDAN 结果Fig.4 CEEMDAN results
通过对比可以看到,与EMD 相比,CEEMDAN的IMF 更多,可以更有效地获得信号的频率分量,且IMF 更集中在特定的频率上。CEEMDAN 的IMF 分量中IMF1 至IMF3 为幅值较低(均值为-0.015 MW)的高频分量,是原始净负荷中波动性难以预测的重要因素,但由于其幅值较低,预测误差在净负荷预测全局中显得非常小。IMF4 至IMF6 为中等频率分量,其幅值均值也在-0.015 MW 附近。IMF7 至IMF9 的频率更低,波动较小,幅值较大,均值为1.221 MW。r为单调曲线,数值较大,幅值均值为32.501 MW。DBN 具有强大的非线性拟合能力,在面对较为平稳的时序数列预测时能够更好地发挥其预测能力。
3.2 某地区配电网净负荷预测算例
本文采用了某地区的实际负荷数据,同样引入当地的气象数据,包括温度、气压、光照、风速等,所选择因素能够影响用户净负荷。为了验证本文所提方法的有效性,选择平均绝对百分误差eMAPE和均方根误差eRMSE用于评判时序数列预测模型,作为评价预测模型准确性的指标,其计算公式为:

式中:yi和分别为第i个时刻的净负荷需求实际值和净负荷需求预测值;N为所有作为测试集的样本个数。从计算公式上可以看到,eMAPE值代表了预测结果偏移的百分比,而eRMSE值代表了预测结果实际偏差的绝对值。eMAPE和eRMSE值越小说明预测效果越好。
净负荷需求在经过EMD 和CEEMDAN 后,分别形成了7 个和10 个IMF 分量,通过DBN 对每个IMF 分量各自的DBN 最佳模型进行独立并行训练,输出预测结果并计算2 个误差指标,如表1 和表2 所示。在使用DBN 独立预测各IMF 分量时,选取日期、时间等要素和温度、风速、光照强度等和负荷强相关的环境因素作为其输入数据,负荷作为预测模型的输出结果,采用贪婪训练法逐一搜索各DBN 的最佳层数与神经单元数的最佳组合,选取前78%作为训练集,剩余部份作为测试集进行模型有效性的验证。可以看到,DBN 在预测高频信号分量时,虽然eMAPE值较大,但由于其幅值较小,产生的代表绝对误差的eRMSE值并不大,因此高频信号分量的预测误差对最后的实际预测结果影响不会太大。在对中等频率和低频信号分量预测时,DBN 能够展现出强大精准的预测能力,特别是对规律性较强、幅值较大的残项,两者的eMAPE值分别达到0.540% 和0.024%,eRMSE值分别为0.057 5 MW 和0.010 6 MW,能够较好地克服传统方法对高频信号难以准确预测的不足,弱化其对最终负荷预测结果准确性的影响。

表1 EMD 各IMF 预测误差Table 1 EMD forecasting error of each IMF

表2 CEEMDAN 各IMF 预测误差Table 2 CEEMDAN forecasting error of each IMF
最后,将每个IMF 分量的预测结果叠加,可以得到最终的净负荷需求预测结果,如图5 所示。

图5 不同算法负荷预测结果Fig.5 Load forecasting results with different algorithms
通过式(13)和式(14)计算可以得到,采用EMD-DBN 和CEEMDAN-DBN 方法得到的最终预测误差eMAPE值分别为4.79%和4.32%,而采用DBN直接预测的误差eMAPE值为5.55%,2 种方法分别将eMAPE值降低了13.69%和22.16%。同时,每个IMF预测的时间均在3 s 以内,足以满足日前净负荷小时级时间尺度的预测需求。此外,本文还将通过对比预测需求的算法,进一步论述分离方案。
3.3 基于CEEMDAN 的净负荷预测算例对比
为对比直接预测净负荷需求和独立预测叠加后的准确性,本文采用6 种常用的机器学习方法进行测试:多元线性回归(MLR)、最小二乘支持向量机(LSSVM)、支持向量回归(SVR)、高斯过程(GP)、LSTM 网络和DBN,分别对比各自独立预测与直接预测效果,并计算本文所用方法的性能提升效果。各个算法采用独立预测方法和直接预测方法的误差如表3 所示,同时给出了采用独立预测算法后对预测模型的性能提升效果。

表3 不同方法预测误差Table 3 Forecasting errors of different methods
与直接预测相比,独立预测提高了4 组预测精度,平均预测误差降低了14.08%。这是因为独立预测不仅基于实测数据,而且借助CEEMDAN 后形成幅值较低的高频信号和幅值较大的低频信号。在高频信号预测时,预测误差尽管偏移百分比较大,但对于净负荷需求整体而言偏移量在可接受范围内。而在低频信号预测时,能够很好地拟合净负荷需求曲线,淡化由高频信号预测引入的误差分量,从而提高了预测精度,进一步验证了分离法的高效性。
4 结语
为了解决用户侧可再生能源发电量无法监测、配电网内部分布式电源不可观而带来的净负荷需求难以精准预测的问题,本文从数据层面出发,将原始净负荷数据分解为若干个频率、幅值不一的时序分量,提出了一种基于CEEMDAN-DBN 的净负荷需求预测方法。通过某地区实际净负荷数据进行测试,可以得出如下结论。
1)CEEMDAN 能够解决EMD 过程中的模态混叠问题,同常用的EMD 方法相比,有效地减少了迭代次数,增加了重构精度,更加适合非线性信号的分析。
2)DBN 通过其强大的特征提取和函数表征能力,在处理高度复杂的隐性非线性时序数据拟合方面展现出明显优势。
3)通过CEEMDAN 可以将原始的非平稳序列分解为若干个幅值较低的高频信号和幅值较大的低频信号,配合DBN 智能算法,适用于非线性非平稳的净负荷需求,有助于降低净负荷需求整体预测误差。
后续研究将结合迁移学习、增量学习等技术手段,实现预测模型对用户侧模态变化的跟踪与学习更新,提高预测模型的适应性与泛化能力。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

