不同重力环境下DFFSR自适应神经鲁棒控制*

武宁宁，孟广耀

(青岛理工大学机械与汽车工程学院，山东 临沂 273400)

0 引言

随着太空探索进程的加快，空间机器人能够代替宇航员出舱活动进行科学实验、空间探测、垃圾回收等任务，大幅降低了太空活动的风险和成本，因而受到广泛的关注和研究[1-3]。为确保系统正常运行，空间机械臂往往需要在地面进行装调试验后才能送上太空，为此，如果不克服地面与空间不同重力环境带来的影响，地面装调阶段的控制方法将无法运用于太空环境中。

当前解决上述问题的办法主要分为两种，一种是通过物理手段实现空间微重力的模拟。如文献[4-6]分别采用气浮法、被动悬吊法、主动悬吊法，通过引入与重力平衡的外力实现太空微重力环境的等效模拟，但此类方法均需构建大量的机械装置，且无法完全消除重力的影响，模拟精度较差。另一种是通过设计控制器，从控制方法上消除重力项对控制精度的影响。如刘福才等[7]提出了一种自适应反演滑模控制方法，较好的克服了不同重力环境的影响。雷霆等[8]提出了一种整体逼近的神经网络自适应控制方法，克服了建模误差以及不同重力等不确定性。刘福才等[9]提出了一种切换控制方法，地面装调阶段采用含重力项的PD控制，空间运行阶段采用不含重力项的PD控制，实现了变重力环境的末端轨迹跟踪控制。但以上均针对的是单臂空间机器人，而DFFSR具备更高的稳定性和更广的操作空间，更具研究价值，庞哲楠等[10]针对双臂空间机器人变重力环境的轨迹跟踪控制问题，设计了一种自适应模糊控制方案，但其模糊建模过程计算量较大。

考虑上述问题，本文针对不同重力环境下的DFFSR轨迹跟踪控制问题，基于传统PI控制方法，设计一种局部模型逼近的自适应RBF神经网络控制方法。根据第二类拉格朗日建模方法，获取双臂空间机器人动力学基本表达形式，利用RBF神经网络的非线性逼近特性，对动力学方程中的惯性矩阵以及重力不确定项进行在线逼近，设计自适应RBF神经网络控制器，并通过引入鲁棒控制项对逼近误差以及外部扰动进行控制补偿。所设计控制器无需建立精确的系统动力学模型，大大减少了计算量，且能够较好的克服重力以及外部扰动对控制器的影响，具有较强的鲁棒性。

1 系统建模

以文献[11]中的双臂空间机器人通用模型为研究对象，如图1所示。

图1 双臂空间机器人系统

其中，M0、M1、M2、M3、M4分别表示系统的基座及4个机械臂，O为系统质心，O-XY为惯性坐标系，Oci(i=0,1,2,3,4)为各分体质心，Oi(i=1,2,3,4)为4个连接铰，ρi(i=0,1,2,3,4)为各分体质心Oci相对惯性坐标系的位置矢量，xi(i=0,1,2,3,4)为基座与机械臂的对称轴，θi(i=0,1,2,3,4)为各对称轴之间的夹角。设O0在O0e0轴上与O1的距离为l0，Mi(i=1,2,3,4)沿轴ei(i=1,2,3,4)的长度为li(i=1,2,3,4)；质心Oci在轴ei上与Oi的距离为ai(i=1,2,3,4)；各分体的质量和中心惯量张量分别为mi和Ji，m=∑mi(i=1,2,3,4)为系统总质量。

当上述系统处于不受外力的自由漂浮状态下时，根据拉格朗日第二类方程，其关节空间动力学方程可表示为[12]：

(1)

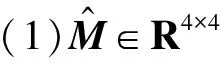
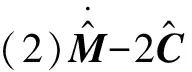
当系统各项惯性参数已知且固定不变时，可通过一般的地面机械臂控制方法实现对空间机器人的轨迹跟踪，而实际上空间环境中，惯性参数容易发生变化且外部干扰不可避免，加之地面和空间的重力环境不同，当考虑上述因素时，动力学方程式(1)又可表示为：

(2)

其中，M、C为实际的惯性参数矩阵，G为系统重力项，f为外界干扰。

2 控制器设计

2.1 经典PI控制器设计

定义轨迹跟踪误差函数、滑模函数以及误差函数分别为：

e(t)=qrd(t)-qr(t)

(3)

(4)

(5)

式中，qr为机械臂实际运动轨迹，qrd为期望运动轨迹，λ=diag(λ1,λ2,λ3,λ4)为常系数矩阵。

若系统惯性参数精确已知，且不考虑外部干扰和重力影响，将上式代入动力学方程式(1)中，则有：

(6)

根据PI控制理论，可设计控制器为：

(7)

为验证该控制器的稳定性，定义Lyapunov函数为：

(8)

对上式求导，结合动力学方程式的性质(2)，则可推出：

(9)

2.2 自适应RBF神经网络控制器设计

RBF神经网络能在一个紧凑集和任意精度下，逼近任何非线性函数，其包含输入层、隐含层和输出层三层结构，网络的输出由如下函数形式实现[13]：

(10)

f(x)=WTφ(x)+ζ

(11)

其中，φ=[φ1φ2…φi]，x=[x1x2…xi]为系统输入，W=[w1w2…wi]为网络权值，ζ为神经网络逼近误差，且有|ζ|≤ζN，σi为节点j的基宽度参数，cj= [cj1cj2…cjn]为神经网络第j个节点的中心矢量。

考虑系统惯性参数未知以及存在重力不确定项，利用神经网络的逼近特性对动力学方程式(2)中的模型不确定部分M、C、G进行逼近，则有：

(12)

(13)

(14)

将上式代入动力学方程式(2)中，则有：

(15)

结合控制律式(7)，设计自适应RBF神经网络控制器为：

(16)

其中，τm为自适应神经网络控制项，τr为用于消除逼近误差以及外部扰动的鲁棒控制项，其表达式分别为：

(17)

τr=Krsgn(s)

(18)

(19)

(20)

(21)

3 稳定性分析

定义Lyapunov函数为：

(22)

(23)

对式(22)求导，结合动力学方程式的性质(2)，则可推出：

(24)

将控制律式(16)以及自适应律式(19)～式(21)代入上式，结合式(23)，整理可得：

(25)

(26)

4 仿真算例

为充分验证本文所提控制方法对不同重力环境下DFFSR系统轨迹跟踪控制精度的有效性和优越性，与传统控制方法进行对比仿真验证。设置系统参数如下。

双臂空间机器人关节角度的期望轨迹分别为：

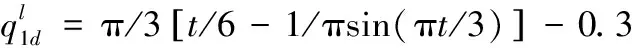
系统运动的初始值为：

选取神经网络隐含层节点数node=5，高斯函数参数cj=[-1.5 -1.0 0 1.0 1.5]，σi=10。选取控制器参数分别为：

λ=diag(5,5,5,5)，Kp=diag(5,5,5,5)
KI=diag(100,100,100,100)
Kr=diag(0.1,0.1,0.1,0.1)

系统重力项和外部干扰分别为：

其中，g=9.8为重力加速度项。

4.1 仿真算例1：传统前馈PD控制方法控制效果

采用经典前馈PD控制方法对两种不同重力环境下的机械臂系统进行仿真，结果如图2所示。

(a) 地面装调阶段机械臂轨迹跟踪

(b) 空间运行阶段机械臂轨迹跟踪图2 PD控制(含重力项)效果

仿真结果图2反应的是采用含重力项的前馈PD控制方法分别对同一机械臂系统处于地面装调和空间运行两个不同阶段时的控制效果。从图2a可以看出，在地面装调阶段由于重力项能够相互抵消，因而控制效果较好，跟踪精度较高，但一旦运送到空间环境中，从图2b可以看出，由于太空中机械臂处于失重状态，此时的控制方法将失效，跟踪过程始终存在较大跟踪误差。

仿真结果图3反应的是采用不含重力项的前馈PD控制方法分别对同一机械臂系统处于地面装调和空间运行两个不同阶段时的控制效果。

(a) 地面装调阶段机械臂轨迹跟踪

(b) 空间运行阶段机械臂轨迹跟踪图3 PD控制(不含重力项)效果

从图3b可以看出，该方法对处于自由漂浮状态下的双臂空间机器人能够实现高精度的轨迹跟踪，但从图3a可以看出，该方法不适用于处于地面装调阶段的机械臂，跟踪精度较差。

若进一步考虑外部干扰，采用与图2a和图3b相同的仿真条件，即采用含重力项的PD控制方法作用于地面机械臂、采用不含重力项的PD控制方法作用于空间机械臂，得到仿真结果如图4所示。

(a) 地面装调阶段机械臂轨迹跟踪

(b) 空间运行阶段机械臂轨迹跟踪图4 PD控制(存在外部扰动)效果

仿真结果图4反应了虽然传统PD控制方法能够通过调整前馈重力项使机械臂在地面或空间中的某一个阶段下实现机械臂的高精度轨迹跟踪，但一旦外界存在扰动，控制效果会受到明显影响。

综上仿真结果表明，传统PD控制方法无法同时保证对地面状态和空间运行两个不同阶段的机械臂控制效果，且鲁棒性较差。

4.2 仿真算例2：本文所提控制方法控制效果

采用本文所提的自适应RBF神经网络控制方法对存在外部扰动且重力环境不同的机械臂系统进行仿真，结果如图5～图7所示。

(a) 地面装调阶段机械臂轨迹跟踪

(b) 空间运行阶段机械臂轨迹跟踪图5 本文方法控制效果

从图5可以看出，在考虑系统存在重力项以及外部干扰的情况下，无论是在地面装调阶段还是在空间运行阶段，所设计的自适应RBF神经网络控制器均能够使双臂空间机器人左右两臂各关节角在t=0.5 s的时间内从初始角度迅速运动至期望角度并实现轨迹持续跟踪，跟踪误差始终控制在较小范围。

(a) 地面装调阶段参数逼近

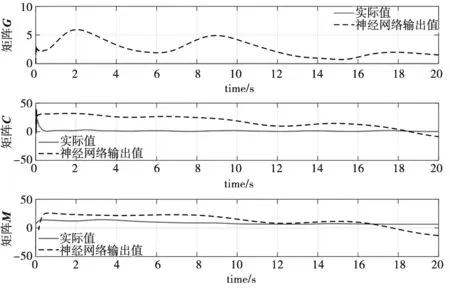
(b) 空间运行阶段参数逼近图6 惯性参数矩阵和重力项范数值逼近

从图6可以看出，无论是在地面装调阶段还是在空间运行阶段，所设计的神经网络控制器对系统惯性参数矩阵M、C以及系统重力项G均具有较好的逼近效果，虽然存在一定的逼近误差，但误差始终有界，满足控制器设计条件。

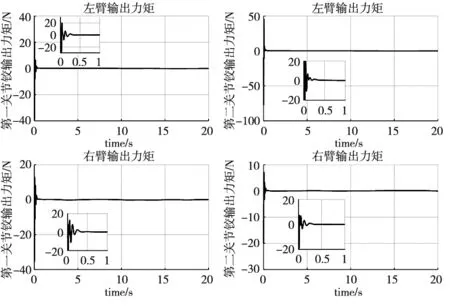
(a) 地面装调阶段关节控制力矩

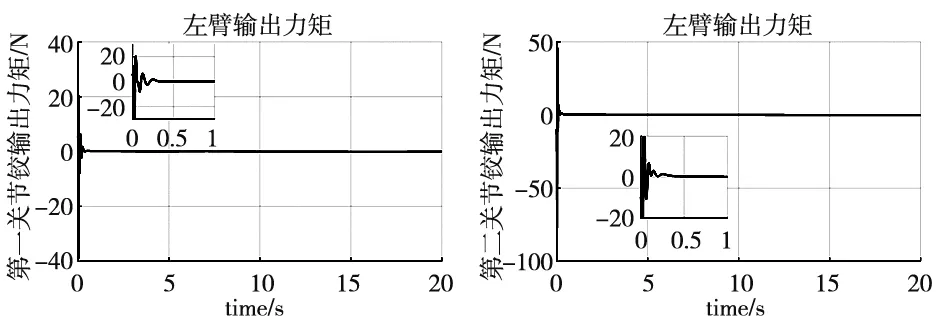
(b) 空间运行阶段关节控制力矩

从图7可以看出，本文控制方法在两个阶段的控制力矩相差不大，且整个控制过程除初始控制力矩较大外，后续跟踪过程控制力矩均很小，满足实际工程需求。

5 结论

本文针对不同重力环境下的双臂空间机器人轨迹跟踪控制问题，基于传统PI控制方法，提出了一种局部模型逼近的自适应RBF神经网络控制方法，实现了机械臂角度的精确轨迹跟踪。所设计控制方法的优点在于：利用神经网络的逼近特性对系统惯性参数矩阵M、C以及系统重力项G进行了在线逼近，从而无需建立精确的系统动力学模型，大大减少了计算量，且能够较好的克服重力以及外部扰动对控制器的影响，具有较强的鲁棒性。