基于中心位的粒子群优化算法

张渊博 邹德旋 张春韵 杜星瀚

摘  要： 针对粒子群优化算法（Particle Swarm Optimization，简称PSO）容易陷入局部极值、进化后期的收敛速度慢和精度低等缺点，提出了基于中心位的粒子群优化算法（Particle swarm optimization algorithm based on center particle，简称CPPSO）。该算法采取双策略更新粒子位置，一种通过随机惯性权重作用的粒子和影响算子作用的个体极值、全局极值来更新粒子位置，另一种在之前更新的粒子位置基础上，通过中心位采用差分算法来更新粒子位置。通过和其他3种优化算法在18个典型基准函数的仿真测试结果表明，该算法具有更好的全局收敛能力，其收敛速度、寻优精度和稳定性都有明显的提升。

关键词： 粒子群优化算法; 随机惯性权重; 简化粒子群优化方程; 影响算子; 中心位; 基准函数

中图分类号：TP301.6          文献标识码：A     文章编号：1006-8228（2021）12-22-05

Abstract： Aiming at the shortcomings of particle swarm optimization （PSO）， such as prone to fall into local extreme values， slow convergence speed and low accuracy in the later stage of evolution， a particle swarm optimization algorithm based on the central particle （CPPSO） is proposed. The algorithm adopts two strategies to update the particle position. One is to update the particle position through the particles affected by stochastic inertia weight and the individual extreme value and global extreme value affected by the influence operator; the other is to update the particle position by using the difference algorithm through the center position based on the previously updated particle position. Simulation test results of 18 benchmark functions with other 3 optimization algorithms show that the proposed algorithm has better global convergence ability， and the accuracy， speed and stability of convergence are significantly improved.

Key words： particle swarm optimization algorithm; stochastic inertia weight; simplified particle swarm optimization equations;influence factor; center position; benchmark function

0 引言

粒子群算法（PSO）是由Kennedy和Eberhart[1，2]在1995年提出的。由于其結构简单、计算量小，粒子群算法已被广泛应用于求解大范围优化问题[3]。该算法已成功应用于解决许多实际优化问题，如路径规划[4]、柔性作业车间调度[5]、特征选择[6]、深度神经网络[7]等。粒子群优化算法虽然原理简单、易于实现、收敛速度快，但仍存在收敛过早、全局搜索能力差等缺点。为了提高粒子群算法的优化性能，许多学者提出了各种各样的粒子群算法变体。这些算法可分为两大类：自适应粒子群算法和混合算法。

自适应粒子群算法主要是对粒子群算法公式进行改进和更新。在后来的研究中实施了一种自我调节权重来调整最佳粒子以改善勘探。其中，张鑫[8]提出的自适应简化粒子群优化算法（Self-Adjusted Simplified Particle Swarm Optimization，简称SASPSO），在每代更新时，通过权重以及全局极值引导来更新位置，并加入锁定因子，使全局历史最优解有规律地引导粒子位置更新。改进惯性权重公式，令其根据当前粒子位置做出自适应配置。不论速度还是精度都得到了提高。赵国新[9]提出的混合自适应量子粒子群优化算法（Hybrid Adaptive Quantum Particle Swarm Optimization，简称HAQPSO），使用收缩—扩张系数随着粒子的适应度值的改变而自适应调整;利用Levy飞行策略的偶尔长距离的跳跃，使得种群多样性增加，提高了跳出局部最优的能力。在Rosenbrock函数问题上得到了很大改进。

混合算法的重点是结合不同算法的优点，来提高粒子的搜索能力。许多学者在这方面做出了突出研究，其中，易文周[10]提出一种结合粒子群和差分演化的两阶段算法，前期用粒子群算法进行全局搜索，后期用差分演化算法进行局部搜索，发挥两种算法的优点而避开各自的短处。李俊[11]提出了一种基于异维变异的差分混合粒子群算法，首先，使用熵度量初始化粒子;其次引入异维变异学习策略和维度因子以引导粒子及时跳出局部极值达到最优解。但是迭代次数很大，有较长的运行时间。

虽然改进的优化算法众多，方法独特，但针对粒子群优化算法快速逃脱局部最优到达理论值的研究仍是值得的。本文采取双策略更新粒子位置，一种通过随机惯性权重作用的粒子和影响算子作用的个体极值、全局极值更新粒子位置，另一种在之前更新的粒子位置基础上，通过中心位采用差分算法更新粒子位置。从而比较两者新粒子的适应度，进而选择好的位置迭代寻优。最后改进算法通过和其他三种优化算法在用18个典型基准函数的仿真测试。

1 基本粒子群优化算法

在PSO中，每个粒子代表多维空间中的一个点，其当前位置用[xtid]表示，其中[i]为单个粒子，[t]为迭代次数。每个粒子的初始位置到目前为止最优解用[pid]表示。算法跟踪的另一个值是全局最优解[pgd]。粒子速度[vt+1id]为每次迭代[t]时粒子位置的变化。简而言之，粒子群优化算法使试图通过更新粒子的速度，使其朝着自身最优解和全局最优解的方向加速。[vtid]和[xtid]都是迭代更新的分别通过以下两个方程：

其中，认知因子[c1]和社会因子[c2]统称为加速系数。[r1]和[r2]是第[t]次迭代生成[（0≤rand≤1）]的随机数，[N]表示种群的大小。[ω]为权重，粒子速度更新方程中存在三个矢量分量;即动量向量，认知或个人成分和社会或全局成分。

2 改进的粒子群算法

2.1 简化粒子群算法

胡旺[12]提出一种简化粒子群优化算法，在原始粒子群算法上，舍去速度项，由个体极值、全局极值和权重共同更新粒子位置，本文在此基础上，提出影响算子，并且加入随机惯性权重更新粒子位置。迭代公式如下：

其中右边的第1项为“历史”部分，表示过去对现在的影响，通过[ω]来调节影响程度;第2项为“认知”部分，表示粒子对自身的思考;第3项为“社会”部分，表示与邻居粒子的比较和模仿，实现粒子间的信息共享以及合作。其中影响算子[e1，e2]表示为：

影响算子能够有效的改变两种极值对粒子位置的更新，并且平衡个体极值与全局极值。粒子的更新前期受个体极值影响大，使粒子快速找到相对较好的位置，寻优中期，一部分粒子向全局最优值靠近，一部分粒子继续搜寻更好的位置点，迭代次数达到后期时，所有粒子向全局最优值靠近，使粒子得到更好的收敛。

2.2 随机惯性权重

惯性权重[ω]是粒子位置更新中重要的参数之一。它起到了一个平衡全局搜索能力和局部搜索能力的作用，恰当的[ω]值可以提高寻优能力，减少迭代次数。本文提出随机惯性权重，表示为：

式中[r]为[（0，1）]之间的随机数;[t]为当前迭代次数;[T]为最大迭代次数;[i]为第[i]个粒子。改进的权重的特性是随迭代次数非线性下降的，使算法具备逃脱局部最优的能力。在后期较小惯性权重，有利于提高局部搜索能力。

3 改进的差分进化算法

差分进化（Differential Evolution，DE）算法是由Storn和Price[13]这二位科学家在1995年提出的一种基于遗传算法的启发式随机搜索算法，具有结构简单、容易实现、收敛速度快、鲁棒性强等优点。本文基于差分进化的变异操作进行改进，改进的公式如下：

式⑺通过中心位与变量[G]随机地生成粒子的一维信息进行差分进化，以达到跳出局部最优的效果。其中[qtid]为采用差分算法更新的新位置，[F]为缩放因子，[xtid]为采用公式⑷更新后的粒子位置。[F]和[G]计算公式如下：

其中[r]为（0，1）的随机数，[t]为当前迭代次数，[T]为最大迭代次数，为了跳出局部最优值，本文基于文献[14]设计一种中心位，跳出局部最优，中心位表示为：

算法实现步骤如下。

Step1 设置最大迭代次数、种群数量、影响算子，初始化种群位置，惯性权重。

Step2 根据适应度函数计算出粒子的适应度。

Step3 比较找出个体极值[Pbest]与全局极值[Gbest]。

Step4 根据式⑷，⑸，⑹，分别计算出影响算子[e1，e2]和惯性权重[ω]。

Step5 根据式⑶更新粒子位置。

Step6 根据式⑺更新出新的粒子位置。

Step7 计算两种粒子的适应度值，更新两种极值。

Step8 判断是否满足终止条件，若满足执行Step9，否则转到Step4。

Step9 输出全局极值[Gbest]。

4 仿真实验

4.1 测试函数

为了检验算法CPPSO的有效性，用18个标准測试函数进行仿真对比，其中函数[f3、f4、f6、f9、f12-f18]为单峰测试函数，函数[f11]在低维情况下为单峰，高维情况下为多峰，[f1、f2、f5、f7、f8、f10]为多峰函数，[f8、f11]为病态的二次函数。测试函数见表1。

4.2 实验参数与测试结果

本文算法的参数设置如下：粒子种群数目40个，粒子维数30维，最大迭代次数为100，每个测试函数算法运行30次，将适应度值取以10为底对数值表示。两种算法的实验数据对比结果见表2。

从表2可以看出，对于测试函数，CPPSO算法基本上优于SASPSO算法，除了[f8]、[f12]的最小值，CPPSO劣于SASPSO，其标准差都比SASPSO小。[f11]函数搜寻最优解极为困难，但CPPSO算法搜寻到了SASPSO算法难以达到的比较好的解。虽然实验结果中[f1、f2、f9、f12]和[f13、f14]相差不是很大，但是[f2、f3、f6、f15、f16、f18]测试函数结果，无论是最小值、平均值，还是标准差，相比SASPSO算法都能搜寻到更准确稳定的解。而且CPPSO算法搜索到[f4、f5、f7、f10]的理论解。

图1-图4是[f3、f8、f17、f18]典型的四个测试函数寻优30次平均适应度的迭代曲线，纵坐标是适应度对数值，可知，[f3、f8]的进化曲线在22代前已经稳定搜索到了比SASPSO算法较好的解。因为SASPSO算法只有全局极值引导的粒子更新，在一些多极值的函数寻优中容易陷入局部最优，导致寻优结果不精确，达不到理论值。CPPSO算法有影响算子作用的双极值和中心位更新的位置信息，从而能够及时地跳出局部最优。

4.3 算法性能分析

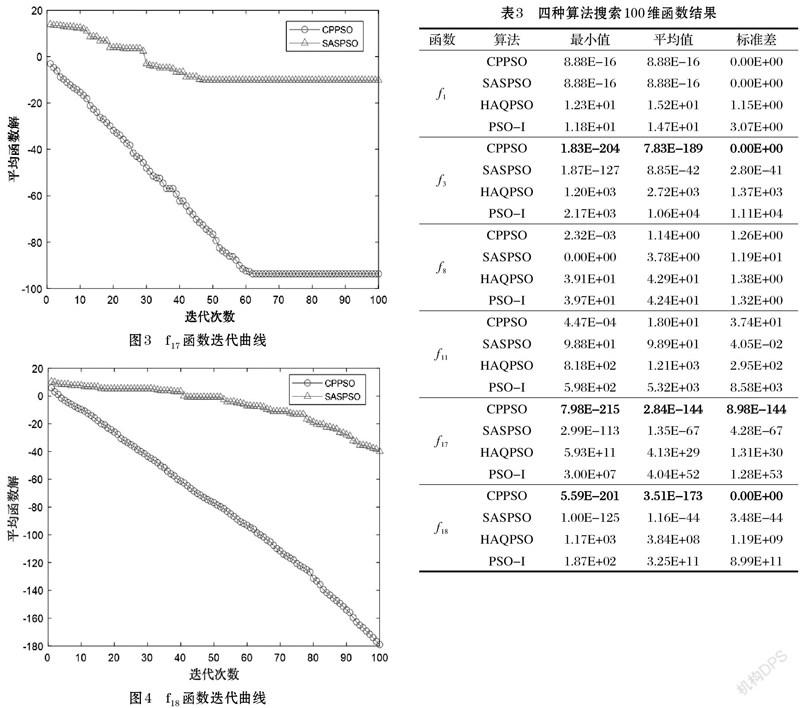
为进一步评价CPPSO算法的性能，对CPPSO算法与近两年的新算法SASPSO、HAQPSO，以及动态调整惯性权重的粒子群算法（A particle swarm optimization algorithm that dynamically adjusts the weight of inertia，PSO-I）[15]算法在100维下进行30次实验分析。在18个测试函数中找到具有代表性的[f1、f3、f8、f11、f17、f18]六个典型测试函数实验。

从表3可知，CPPSO算法无论是最小值、平均值，还是方差都比其他三种算法优秀，除了[f8]，SASPSO算法搜索到了理论解，但很不稳定。维数的增加提高了算法寻优的复杂度，而对CPPSO算法影响不大，通过六个典型的测试函数可知，粒子维数的增加，对算法寻优精确度影响不大。

5 结束语

本文针对粒子群优化算法在迭代的后期会出现种群多样性不足导致易陷入局部最优的问题，提出三点改进，首先，加入影响算子随迭代次数，平衡了局部和全局搜索能力，使算法能很好的搜寻到较好的最优值，然后通过随机惯性权重更新粒子位置，使算法很好的从全局寻优过渡到局部寻优，最后采用中心位改变粒子位置，使算法逃脱了局部最优，并且是算法找了更好的解。通过18个测试函数的实验结果和与参考文献中的方法进行比较可得，CPPSO算法的表现较好，改进的方法提升了算法的全局搜索能力，提高了稳定性以及收敛的精度。但针对个别测试函数算法仍存在陷入局部最优的问题，之后研究应对该问题深入了解，运用不同的局部搜索方法增加算法收敛精度。

参考文献（References）：

[1] Kennedy J，Eberhart R.Particle swarm optimization[C].Proceedings of 1995 IEEE International Conference on Neural Networks.Piscataway，NJ：IEEE Press，2002：1942-1948

[2] Shi Y，Eberhart R C.Empirical study of particle swarmoptimization[C].Proceedings of the 1999 Congress on Evolutionary Computation.Piscataway，NJ：IEEE Service Center，1999：1945-1950

[3] 邵晴.粒子群算法研究及其工程应用案例[D].吉林大学，2017.

[4] 陈嘉林，魏国亮，田昕.改进粒子群算法的移动机器人平滑路径规划[J].小型微型计算机系统，2019.40（12）：2550-2555

[5] 尉雅晨.改进粒子群算法研究及其在柔性车间调度问题中的应用[D].兰州理工大学，2020.

[6] 邓瀚浡.大规模粒子群算法及其在视频流量特征选择中的應用研究[D].济南大学，2019.

[7] 黄荣煌.采用粒子群算法优化深度神经网络压缩的研究[D].厦门大学，2019.

[8] 张鑫，邹德旋，肖鹏，喻秋.自适应简化粒子群优化算法及其应用[J].计算机工程与应用，2019.55（8）：250-263

[9] 赵国新，陈志炼，魏战红.混合自适应量子粒子群优化算法[J].微电子学与计算机，2019.36（7）：76-80，86

[10] 易文周.基于差分演化和粒子群优化的改进WSN覆盖算法[J].计算机与现代化，2019.8：33-38，62

[11] 李俊，罗阳坤，李波，李乔木.基于异维变异的差分混合粒子群算法[J].计算机科学，2018.45（5）：208-214

[12] 胡旺，李志蜀.一种更简化而高效的粒子群优化算法[J].软件学报，2007.4：861-868

[13] Storn R. Differrential evolution-a simple and efficient adaptive scheme for global optimization over continuous spaces[J].Technical report， International Computer Science Institute，1995.11.

[14] Xiaojing Y， Qingju J， Xinke L. Center Particle Swarm Optimization Algorithm[C].2019 IEEE 3rd Information Technology， Networking， Electronic and Automation Control Conference （ITNEC）.IEEE，2019：2084-2087

[15] 吴静，罗杨.动态调整惯性权重的粒子群算法优化[J].计算机系统应用，2019.28（12）：184-188