基于VMD的水电站厂房结构模态参数识别研究

方国富，黄文龙，王海军，郭飞飞

（1.福建厦门抽水蓄能有限公司，福建 厦门 361000；2.天津大学建筑工程学院，天津 300350）

为了满足我国对可再生能源发展的需求，近年来水电开发得到了快速发展，兴建了一大批大型的常规电站和抽水蓄能电站。机组的单机容量已经突破了百万千瓦，并在白鹤滩水电站得到了应用。所带来的问题是机组、厂房结构的运行安全问题更加突显。进行厂房结构动力安全评估需要获得结构准确的模态参数。因此，如何准确获取厂房结构精确的模态参数，对水电站厂房的智能化运行监测、安全评估等非常重要。

近20 a 来，结构模态参数识别领域的研究无论是理论方面还是应用方面都得到了长足发展。国内外学者开展了广泛的研究。Lawrence 等[1]提出了一种利用拉普拉斯小波将信号分解模态参数的估计方法，并应用于飞机机翼动力响应分析，效果良好。吕志民等[2]采用非线性模型和小波变换方法组合，成功地识别了水轮机轴系的模态参数。张志宜等[3]提出了一种基于Gabor 变换的模态参数识别方法。吴长智等[4]提出了一种基于模糊优化的信号非线性参数识别方法，准确地识别出了结构的模态参数。Dragomiretskiy K和Zosso D[5]2014年提出了变分模态分解方法（VMD），该方法可将一输入信号分解成多个变分模态分量，各分量围绕中心频率并且各变分模量具有稀疏性[6-9]，同时该方法具有良好的抗噪性能和抗模态混叠性能。水电站厂房结构包括各种孔洞、板梁体系，空间结构复杂，引起振动的振源包括水力、机械、电磁等，荷载繁多，因此对水电站厂房结构进行模态识别，噪声、模态混叠难以避免。

本文依托现场振动实测数据，将VMD 与随机减量法、STD 等方法相结合，开展水电站厂房结构模态参数的精确识别研究。

1 基于VMD的信号分解

VMD 可视为一个信号分解过程。具体步骤如下：①采用Hilbert 变换进行模态分解，得到各模态分量的单边频谱；②将各模态分解信号与预估指数项进行混合；③采用高斯估计分析信号的模态带宽。其表达式即为式（1）所示的约束变分方程。

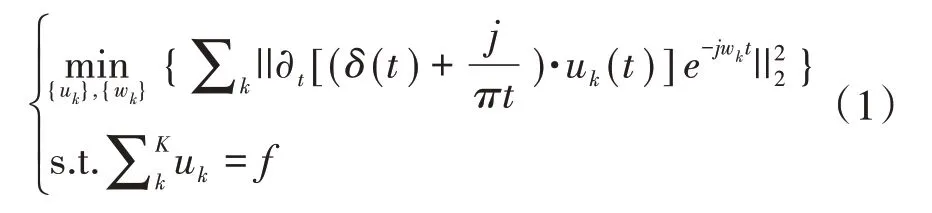
式中：f为信号；{uk}={u1,…,uk}为模态分解信号集合；{ωk}={ω1,…,ωk}为中心频率集合；K为分解层数[10]。

为求得式（1）的最优解，引入二次罚项因子α和拉格朗日乘法算子λ，可得表达式（2），具体求解流程如图1所示。

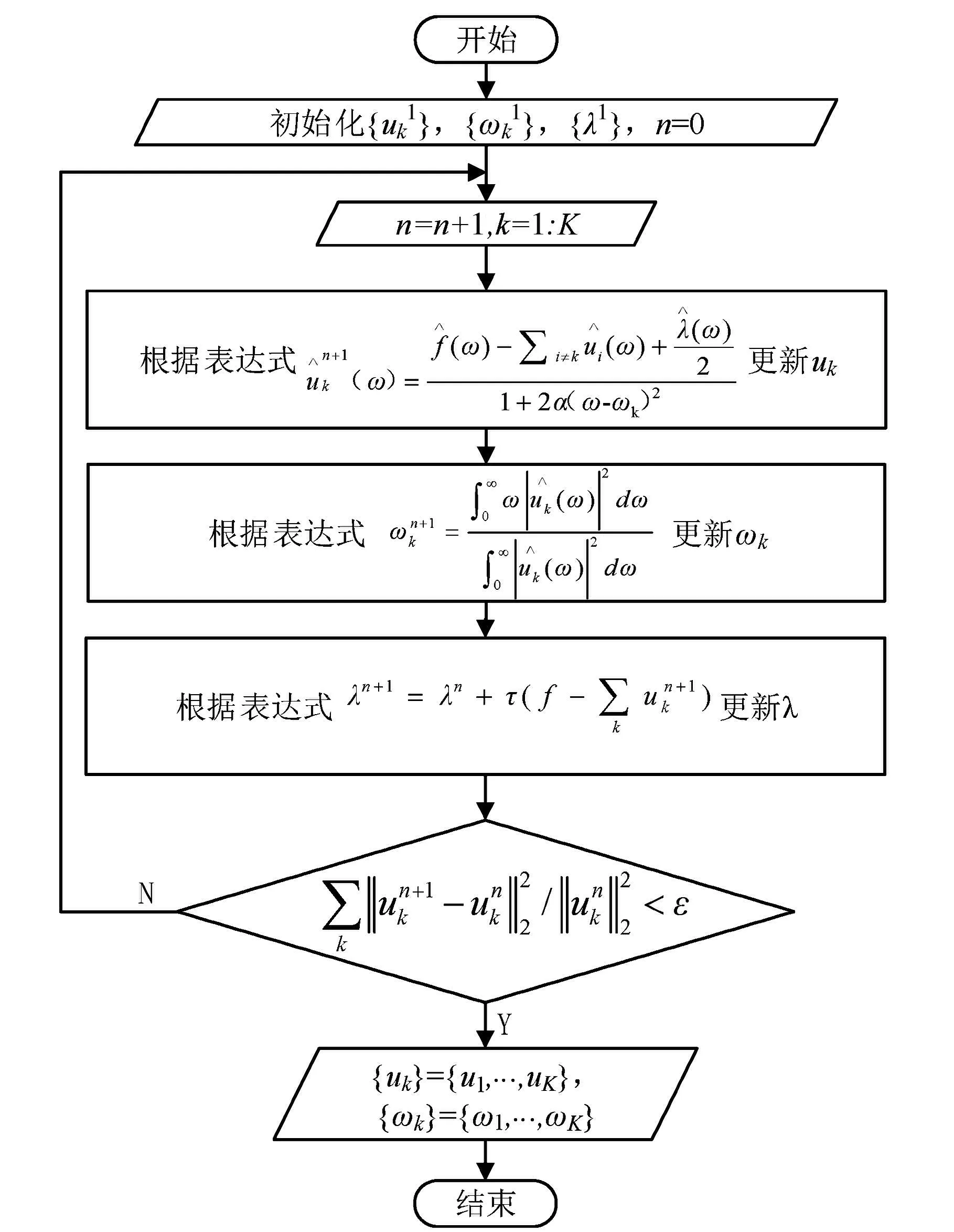
图1 VMD流程

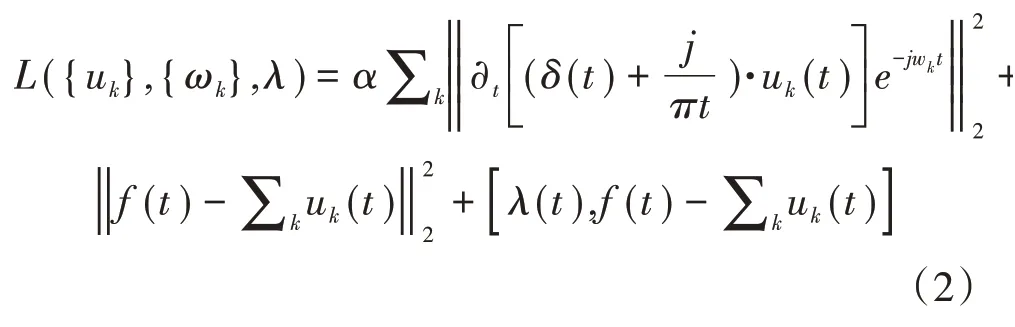
2 仿真信号模拟验证

根据上述的方法开发了相应的程序，为验证程序的合理性以及VMD 方法的抗混叠性能和抗噪性能，分别构造包含间断信号的仿真信号和包含噪声信号的仿真信号进行验证。

2.1 抗混叠验证

仿真信号x1(t)由正弦信号x11(t)和余弦间断信号x12(t)组成。正弦信号的频率为10 Hz，余弦信号的频率为100 Hz。仿真信号如式（3）所示，仿真信号x1(t)的时程线如图2所示。

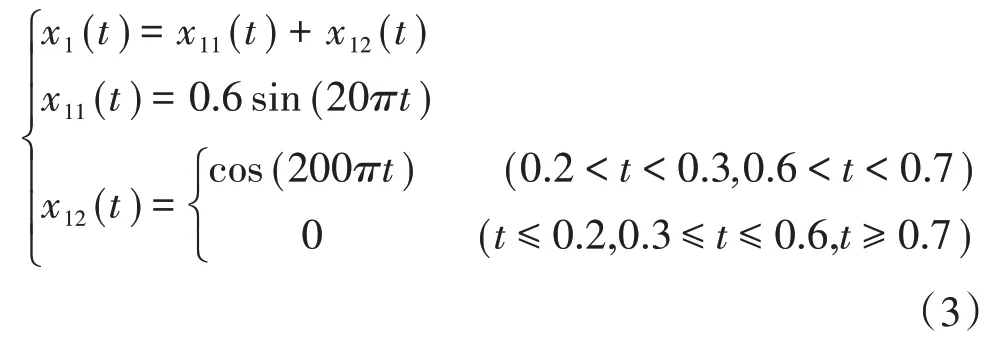
图2 仿真信号x1 ( t )时程线

采用VMD 方法对信号进行分解，分解的层数K设置为2，分解的结果如图3所示。

图3 仿真信号x1 ( t ) VMD分解

从图3 可以明显看出，正弦信号以及余弦间断信号非常完整地进行了分离。图中u1对应正弦信号x11(t)，u2对应余弦间断信号x12(t)。程序经过13次迭代，获得了2 个中心频率，分别为9.8、100.2 Hz，且运算时间很短。与已知的构造信息比较，频率的误差分别为2%、0.2%，识别精度较高，可以满足工程的需求。由此可见，采用VMD方法可以较好地将混叠信号进行分解。

2.2 抗噪验证

为了验证VMD 方法的抗噪性能，构造含噪仿真信号x2(t)，其由x21(t)、x22(t)2 个余弦信号和x23(t)高斯噪声随机信号组成，如式（4）所示。余弦信号频率分别为10、40 Hz。信号时程线，如图4 所示。VMD分解层数K取为3，VMD分解如图5所示。

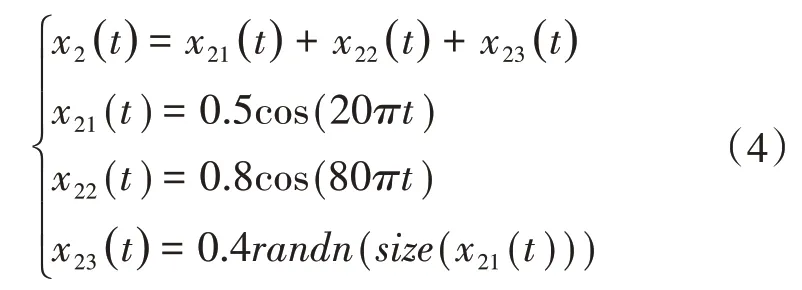
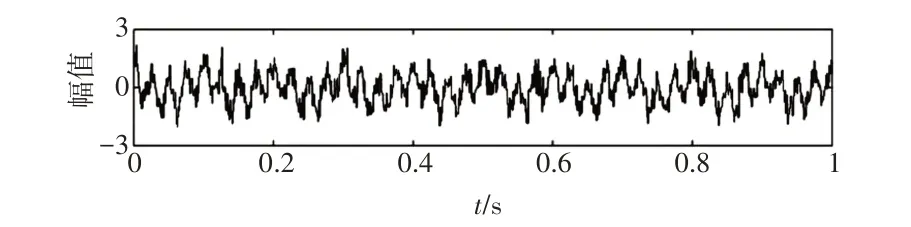
图4 仿真信号时程线

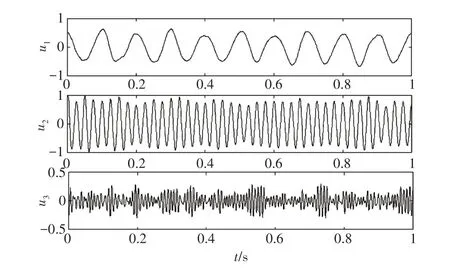
图5 仿真信号VMD分解

各分量与信号x21(t)+x22(t) 的相关系数，详见表1。

表1 相关系数

由表1可知，前2阶的模态分量与不含噪原信号的相关性较大，相关系数分别为0.519和0.836；而第3 阶的相关系数很小，为0.001。因此，选取u1、u2两层信号进行信号的重构，分析认为第3 阶信号为噪声信号。信号的重构相当于对噪声的识别，并进行去噪滤除。

为了验证方法的抗噪性能，引入信噪比SNR和均方根误差RMSE2 个指标作为识别合理性判断依据，两指标如式（5）所示：

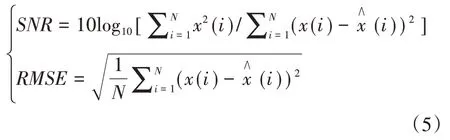
式中：x(i)为原信号；(i)为重构信号；N为信号长度。

经过程序的多次迭代，可以得到模态的中心频率为10、40 Hz，两频率值与仿真信号完全一致。

为了比较该方法的抗噪性能，文中采用常用的经验模态分解方法（EMD）进行了计算，并对2 种方法进行对比分析。2种方法的SNR和RMSE值，详见表2。

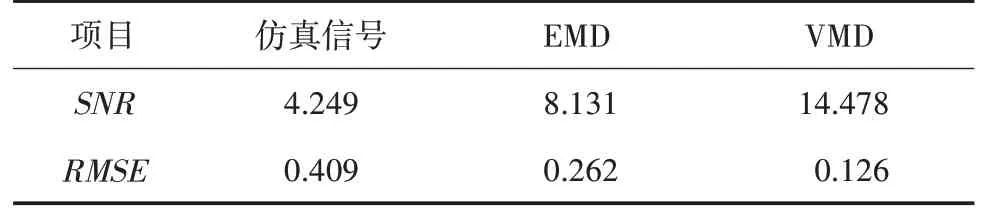
表2 信噪比和均方根误差对比

由表2 可知，VMD 方法SNR为14.478，RMSE为0.126；EMD 方法SNR为8.131，RMSE为0.262。与EMD 方 法 比 较，VMD 方 法 的SNR增 大 了6.347，RMSE减小了0.136。因此，可知VMD 的抗噪性能相对更优。

3 厂房结构模态参数识别

在采用仿真信号验证VMD 方法的有效性后，将该方法应用于实际的水电站工程，以期为水电站工程的安全评价提供参数支持。工程背景为：一大型水电站总装机容量为2 400 MW，厂房为地下厂房，尺寸为243.44 m×31.1 m×76.3 m（长×宽×高），空间巨大。引水发电建筑物主要包括地下厂房、主变洞、出线洞、母线洞、进水口、压力管道等，厂房的空间结构复杂。日常运行中，可监测到厂房局部结构振动偏大，因此需获取准确的厂房结构模态参数，进一步对厂房结构的安全进行评估。

水电站厂房结构一般都非常巨大，孔洞较多，通过人工激励方法来获取结构的激励振动信号是难以实现的。文中采用机组停机过程中机组制动所产生的突变荷载作为激励，测试停机过程中的厂房结构振动位移响应。在厂房结构和机组上布置了13 个测点、7 支传感器，包括振动位移传感器和水压脉动传感器。限于篇幅，选取电站厂房机墩结构上的水平振动信号，信号时程线如图6 所示。信号的采集频率为512 Hz，VMD分解的层数设为5层，采用上述方法和开发的程序可以得到相应的模态分量，如图7所示。

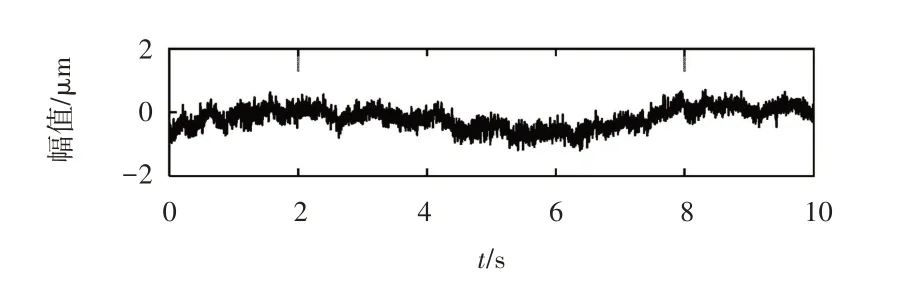
图6 实测信号时程线

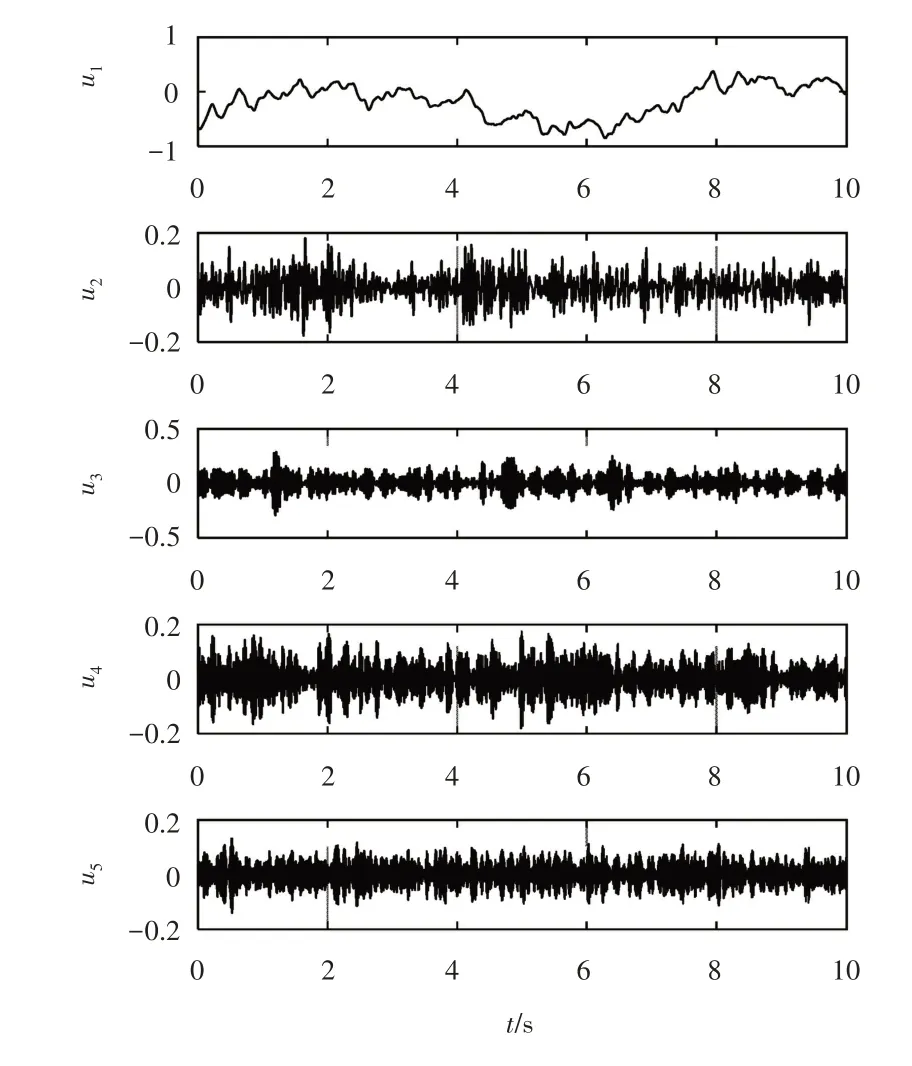
图7 实测信号VMD分解

为了获取准确的厂房结构频率和相应的阻尼，文中提取了VMD 分解的模态分量中与原信号相关性高的3个分解信号。VMD方法可以获取模态中心频率，但无法获取相应阻尼比。因此，引入随机减量和STD方法来组合识别阻尼比。该方法也可以识别各模态分量对应的频率，其频率值与中心频率值是一致的。采用组合方法识别出来的该电站厂房结构自振频率和阻尼比，详见表3。识别出该厂房结构1阶频率为19.26 Hz，前3阶的阻尼比在1.78%～2.56%。采用多个位置测点识别结构与表3 是一致的，在此不再赘述。

表3 自振频率和阻尼比

为了进一步验证识别结果的合理性，选取厂房结构一机组段，采用有限元方法进行三维数值模拟，并进行模态分析。主体结构采用实体单元，钢蜗壳采用壳单元，机组等设备采用质量单元。仿真模型范围为：上下游混凝土墙向外延伸至1 倍厂房宽度的围岩，向上至发电机层楼板，下部从尾水底板向下延伸至1倍厂房高度的围岩，两侧至机组段分缝处。约束条件为：机组段分缝处为自由状态，围岩底部全约束，四周围岩为法向约束[11]。混凝土结构动弹性模量取36.4 GPa，容重为25 kN∕m3；钢结构动弹性模量取210 GPa，容重为78.5 kN∕m3；围岩动弹性模量取20 GPa，容重为27 kN∕m3。模型实体，如图8所示。

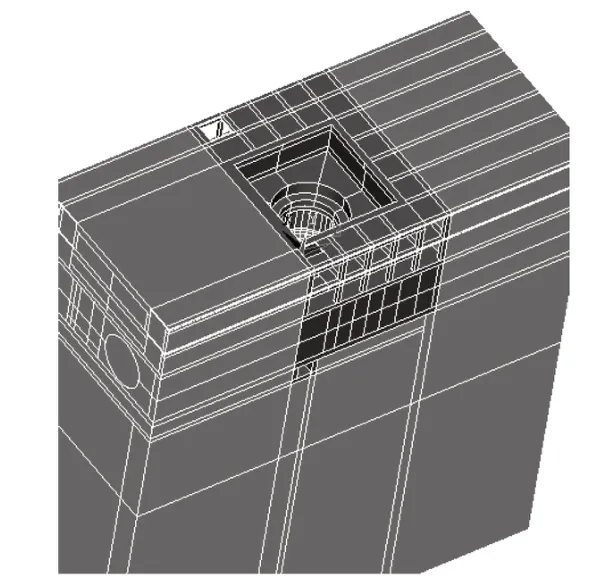
图8 整体模型实体

三维有限元模态分析计算结果，详见表4。

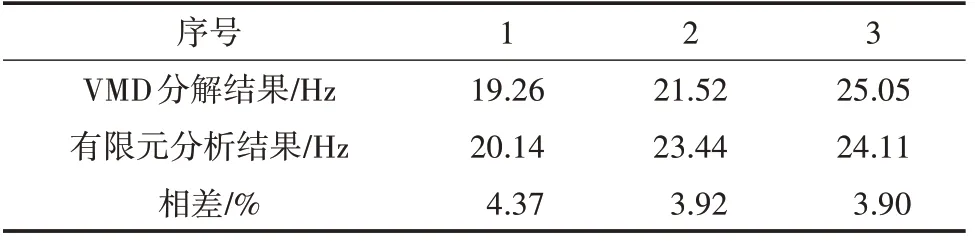
表4 自振频率对比结果

由表4 可知，采用基于VMD 方法的模态参数识别方法对实测振动信号进行分析得到的厂房结构自振频率值与有限元模态分析结果基本一致。前3阶频率值比较最大相差4.37%，识别方法和有限元方法互相验证。由此可见，基于VMD 分解的结构模态参数识别方法具有很高的准确性。

4 结论

（1）VMD 方法能有效地分解各类信号，具有良好的抗模态混叠的能力和抗噪性。

（2）依托水电站厂房振动原型观测数据，采用基于VMD 的模态参数识别方法准确地识别出了结构的前3 阶自振频率和对应阻尼比，为厂房结构的耦合动力安全评估提供了相关模态参数。