基于GM(1,1)季节指数模型的快递业务量预测

王 芳,叶耀军

(浙江科技学院 理学院,杭州 310023)

自从中国在改革开放初期同日本签署的第一份快递代理协议开始,快递这一新型的运输形式才进入民众的视野。在随后不到30年的时间里,快递行业就发展得风生水起。从最初的邮政快递(Express Mail Service,EMS)到如今的申通、圆通、顺丰等民营快递企业,快递行业的前景十分光明[1]。

目前,有不少研究者运用不同评价方法和模型分析预测了快递行业的影响因素和发展潜力。孙丽等[2]指出快递业务量是量化快递行业的一个重要指标,对其进行建模预测,有助于企业高管做出正确的决策。肖烯岚等[3-5]提出快递行业有着发展迅速、跨度空间大等发展特点,认为未来几年之内应提高快递分拣技术,以及快递运输效率。邹志云等[6-7]运用灰色关联度评价法分析了各个指标的权重,确定了应急物流的路径选择,表明物流产业在未来发展中的多样性。除此之外,研究者还从定量角度进行快递需求量预测,如利用差分整合移动平均自回归模型(autoregressive integrated moving average model,ARIMA)和误差反向传播算法模型[8-10]进行快递业务量的预测,预测效果良好。为了减少误差,王惠婷等[11-12]在ARIMA模型的基础上加入二次指数平滑模型和多项式指数预测模型进行组合预测,发现组合模型预测的精度更高。以上研究成果为本研究运用季节指数模型提供了理论基础。

通过对现有文献的整理,发现关于快递业务量的预测研究,大多是单独使用GM(1,1)模型、ARIMA模型或者神经网络等算法定量分析,较少利用组合模型进行业务量的预测。2014—2019年的快递业务量明显呈季节性周期变化,若单独使用GM(1,1)模型,则精度并不会很高,而且只能反映序列的总体变化趋势。因此,本研究应用季节指数修正的GM(1,1)模型进行预测,从而得到更好的预测效果。

1 2种预测模型的建立

1.1 GM(1,1)模型的建立

灰色模型[13-14]主要适用于数据结构分布不明确、信息量少的非典型过程,其优点在于不需要大量的数据。其中GM(1,1)模型结合微分方程和差分方程的特性,能较好地描述序列的内部特征和发展趋势。建模步骤如下:

给定观测数据序列X(0)=(X(0)(1),X(0)(2),X(0)(3),…,X(0)(n)),其中X(0)(k)≥0,k=1,2,…,n。接着对观测序列进行累加生成一次累加生成算子序列(one-accumulating generation operator,1-AGO):

X(1)=(X(1)(1),X(1)(2),X(1)(3),…,X(1)(n));

(1)

(2)

构造数据矩阵B和Y:

(3)

(4)

式(4)所对应的时间相应函数为

(5)

式(5)通过累减算出预测值

x(0)(k)=α(1)x(1)(k)=x(1)(k)-x(1)(k-1),k=1,2,3,…,n。

(6)

1.2 GM(1,1)季节指数模型的建立

原序列的观测值除以季节指数后得到一组没有季节性波动的平稳光滑序列,然后以平稳光滑序列为基础建立预测模型,计算出的模拟值乘以季节指数,恢复其季节波动,进行结果分析。以下是求季节指数的方法,假设数据量为n,季节性波动周期为N(一般为一年的季度数4或者月数12)。

1)求时间序列移动平均值

(7)

2)计算中心移动平均值

(8)

3)计算比例因子

(9)

4)比例因子乘以100后取平均值,调整平均比例,使各季度的平均值等于100N,即得到季节指数。

1.3 精度检验

根据文献[15],主要采取以下3个指标进行模型的精度检验,精度检验公式见表1。P是模型的预测值,Z是原始值,n是预测数据量。

表1 精度检验公式

2 实例分析

本文从文献[16-17]获取2014—2019年的全国快递业务量的季度数据(表2),以表2数据为基础,运用灰色系统理论软件和Excel软件分别建立GM(1,1)模型和GM(1,1)季节指数模型。最后,计算出精度指标,选出最优的预测模型。

表2 2014—2019年的全国快递业务量的季度数据

2.1 GM(1,1)预测模型分析

根据表1,给出原始数列

X(0)=(26.1,33.0,34.8,45.8,37.0,47.6,52.4,69.7,57.8,74.8,78.5,101.9,75.8,97.2,100.7,126.6,99.2,121.6,126.6,159.7,121.4,156.0,165.5,196.1)。

通过式(2)计算出1-AGO序列

X(1)=(26.1,59.1,93.9,139.7,176.7,224.3,276.7,346.4,404.2,479.0,557.5,659.4,735.2,832.4,933.1,1 059.7,1 158.9,1 280.5,1 407.1,1 566.8,1 688.2,1 844.2,2 009.7,2 205.8)。

通过式(3)计算出a=-0.070b=36.902,得到预测模型

x(1)(k)=553.271 428 57e-0.070k-527.171 428 57,k=1,2,3,…,n。

通过式(6)累减还原,得出预测值

x(0)(k)=x(1)(k)-x(1)(k-1)=(40.110,43.013,46.126,49.464,53.044,56.883,60.999,65.414,70.148,75.225,80.669,86.507,92.767,99.481,106.680,114.401,122.680,131.559,141.079,151.289,162.238,173.980,186.571)。

2.2 GM(1,1)季节指数预测模型分析

数据n=24,季节性波动周期N=4,用Excel软件计算季节指数,过程见表3～4。原始序列根据季节指数去掉季节性波动后得到一组新的建模序列,利用灰色系统理论软件建立GM(1,1)季节指数模型,最终得到模型参数a=-0.067,b=38.208,预测模型方程为

表4 季节指数计算表

656 716 4e-0.067k-570.268 656 71,k=1,2,3,…,n。 (10)

2.3 2种模型的精度评价

2种模型2014—2019年的快递业务量拟合值与实际值的精度对比见表5,拟合效果如图1所示。

表5 2种模型精度对比

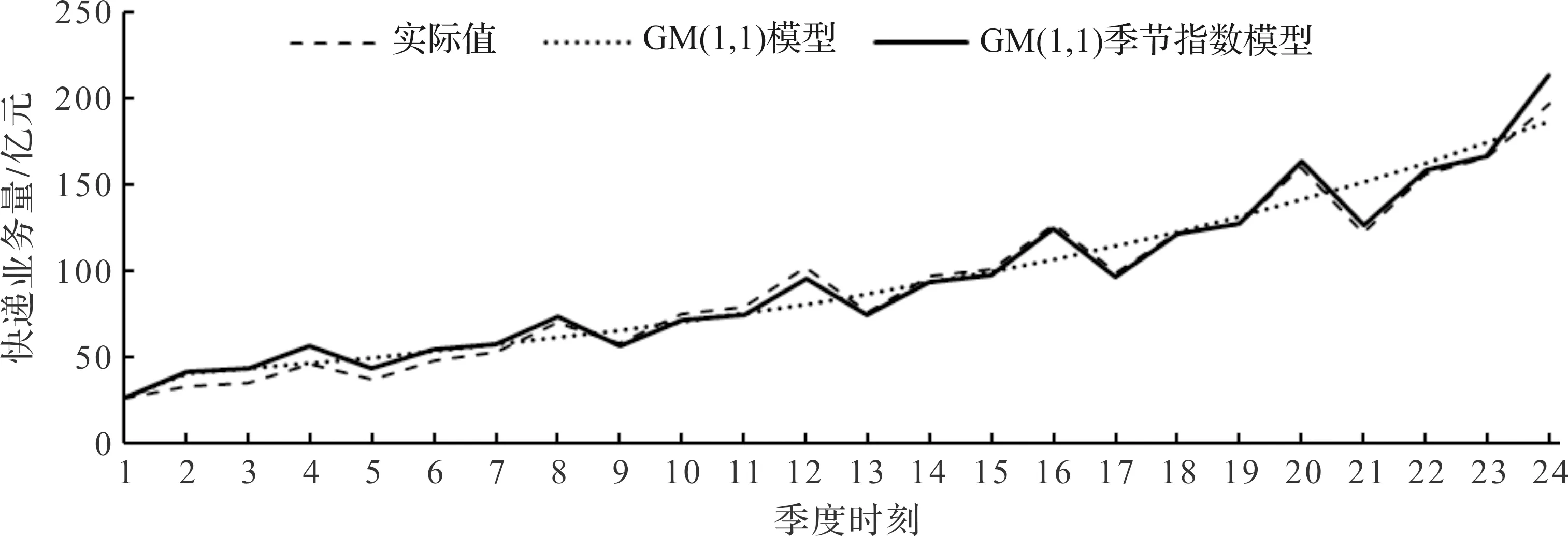
图1 2014—2019年各季度快递业务量拟合效果

根据表5,GM(1,1)模型仅仅反映了总体趋势并没有体现出季节因素,精确度很低,加入季节指数后的GM(1,1)模型,不仅反映了快递业务量的总体趋势,而且精度指标平均绝对误差、均方差和平均绝对百分误差降低了36.840%,74.547%和50.314%。

从图1可以明显地看出,GM(1,1)季节指数模型拟合值比GM(1,1)模型更贴近实际值,图1中的GM(1,1)模型模拟出来的发展趋势表明全国的快递量会持续上涨。结合这几年的形势,在电商、外贸等行业的背景下,快递运输业的业务量大概率会出现新的增长。季节时刻的变化可以说明,每年的第四季度是业务量的高峰,这说明商家的双十一、双十二等促销活动在很大程度上吸引了消费者的目光,从而影响到快递行业的业务量。

2.4 GM(1,1)季节指数模型的预测结果

运用式(10)累减还原计算出2020—2024年全国快递季度业务量预测结果,如图2所示。

图2 2020—2024年全国快递季度业务量预测结果

由图2可以看出,未来几年的快递业务量迅猛增长,展现了消费市场的蓬勃活力。总体来看,在未来的一段时间内快递行业将维持高景气状态,预计2024年快递业务量将超过两千亿件。

3 结 语

本研究以国家统计局、国家邮政局对全国快递量的有关统计数据为基础,应用灰色模型预测快递业务量。先利用2014—2019年的季度快递业务量求出季节指数,接着建立GM(1,1)季节指数模型。通过与GM(1,1)模型对比,得出GM(1,1)季节指数模型精度高于GM(1,1)模型,平均绝对误差降低了36.840%、均方差降低了74.547%、平均绝对百分误差降低了50.314%。通过绘制模拟数据与实际数据的拟合图,得出GM(1,1)季节指数模型计算出的模拟值更接近实际值,能够很好地预测快递业务量。