虚拟同步发电机参数自适应控制策略

程国栋,邵宣,王贵峰

（1.中国矿业大学徐海学院，江苏徐州 221008；2.中国矿业大学电气与动力工程学院，江苏徐州 221008；3.江苏师范大学电气工程及自动化学院，江苏徐州 221008）

0 引言

随着配电网中可再生能源的发电占比逐年提高，大量逆变器接入到电力系统中，这导致电力系统的总惯性下降、稳定性受到严重影响[1]，[2]。利用虚拟同步发电机（Virtual Synchronous Generator，VSG）控制技术，可以为微电网提供类似同步发电机的惯性和阻尼特性，进而维持逆变器输出频率和功率的稳定[3]，[4]。

VSG并不是真正物理上的机械惯量，但VSG的虚拟惯量和阻尼灵活可变，可采用参数自适应的控制策略来提高VSG的运行性能。文献[5]提出一种自适应惯性控制策略，根据不同的工况实现功率调节与频率调节之间的平衡，同时给出了参数的设计原理，确定自适应的范围。文献[6]考虑外界频率波动对系统的冲击，分析配电网频率突变时，不同转动惯量对逆变器输出频率的影响，设计合适的惯性控制策略，实现频率的快速响应。文献[7]在多VSG并联的微电网中提出改进的转动惯量自适应控制，有效抑制了并联VSG带来的功率振荡，但其并未考虑阻尼变化对系统的影响。文献[8]提出一种自适应控制策略，在运行过程中使系统保持最佳阻尼比，用以优化超调以及响应时间等指标，进而抑制频率和功率的振荡，提高了VSG的动态性能。文献[9]提出一种使用模糊逻辑的自适应虚拟惯性控制方法，以保证系统在高渗透条件下运行所需的频率稳定性。该方法根据有功功率和系统频率偏差自动调整虚拟惯性常数，避免了参数选择不当，实现了快速的惯性响应。文献[10]根据负载扰动情况改变转动惯量的大小，进而调节系统的频率响应，但其并未给出转动惯量的具体表达式。

上述文献均只对转动惯量进行自适应控制，没有考虑阻尼系数的影响。本文提出一种基于模糊控制的双参数自适应控制策略。通过分析VSG的功角特性，确定转动惯量和阻尼系数的选取原则；根据角速度偏差量及其变化率来确定模糊规则，实现转动惯量和阻尼系数的自适应调节，进而抑制频率和有功功率的波动，提高系统的动态性能。

1 虚拟同步发电机的数学模型

虚拟同步发电机的控制框图如图1所示。系统主控部分为三环控制。外环为VSG功率控制环，是VSG控制的核心部分，由频率控制和电压控制组成，提供电压和频率支撑；内环为双闭环控制，用以稳定VSG的输出电压，提高系统抗扰性能，加快电流动态响应。将双闭环输出的电压信号传送到SVPWM调制环节，便得到开关管的驱动信号。

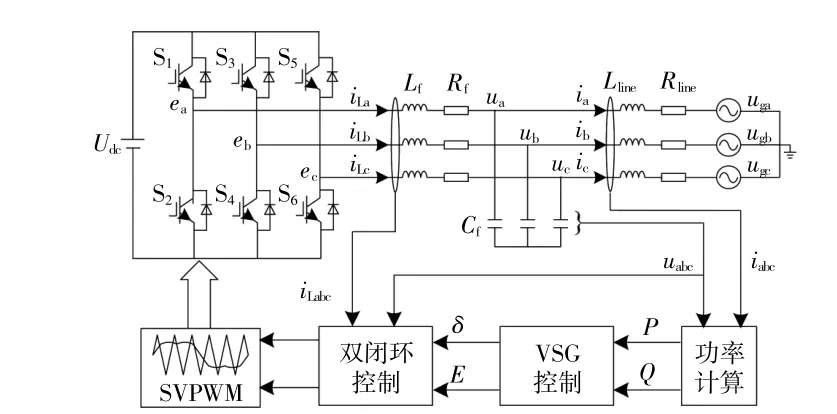
图1 虚拟同步发电机的控制框图Fig.1 Control block diagram of VSG

VSG的频率控制可通过转子运动方程实现。为便于逆变器的控制，对同步发电机的模型进行降阶处理，采用经典二阶模型对虚拟同步发电机进行建模，可得转子运动方程为

式中：J为转动惯量；ω为转子角速度；ω0为额定角速度；Pm为VSG机械功率；P为VSG输出功率；D为阻尼系数；δ为VSG的功角。

转子运动方程通过模拟转矩的不平衡来实现转子的加速和减速，虚拟转动惯量J可抑制频率的波动，阻尼系数D可增强系统的抗扰能力。根据同步发电机的无功调压特性，可得到VSG的电压控制方程为

式中：Um为系统电压参考值；U0为额定电压；Q为VSG的无功功率；Qref为无功功率指令值；Kq为无功下垂系数。

在下垂控制基础上，加入励磁调节控制，用于维持VSG输出电压的稳定，励磁调节控制方程为

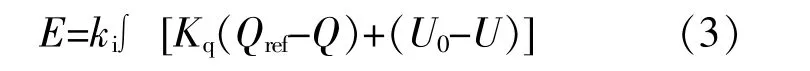
式中：E为励磁电动势；ki为积分系数；U为VSG实际输出电压。

由式（1）和式（3）可得VSG的控制框图，如图2所示。

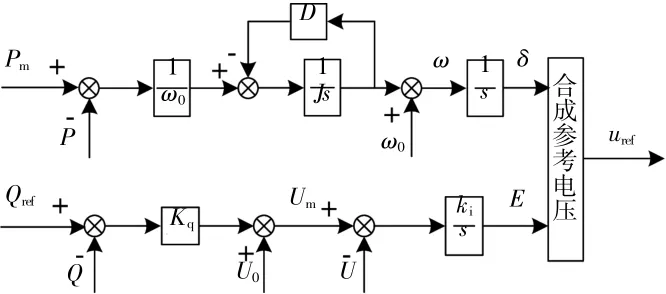
图2 VSG的频率和电压控制Fig.2 Frequency and voltage control in VSG

由图2可知，在逆变器控制策略中加入同步发电机的特性，可提高微电网输出频率和电压的稳定性。

2 转动惯量和阻尼系数对VSG的影响

VSG技术不仅具有调频、调压特性，还能克服电力电子设备带来的缺陷，使微电网具备转动惯性和阻尼。然而，VSG的外特性受转动惯量J和阻尼系数D这两个关键参数的影响较大，为了获得更好的运行性能，须对上述两个关键参数进行详细分析。

2.1 关键参数对输出功率的影响

根据图2可得VSG有功环的控制框图，如图3所示。

图3 有功环控制框图Fig.3 Control block diagram of active power loop

图中：Pref为参考有功功率；P为VSG输出有功功率；U为VSG输出电压；Ug为电网电压；X为系统等效阻抗。

由图3可得VSG有功环的闭环传递函数为

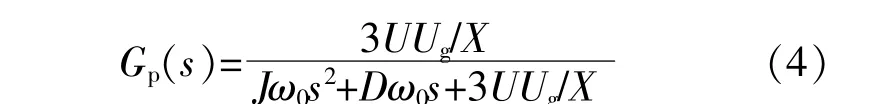
根据式（4）可得VSG输出有功功率的单位阶跃响应曲线，如图4所示。

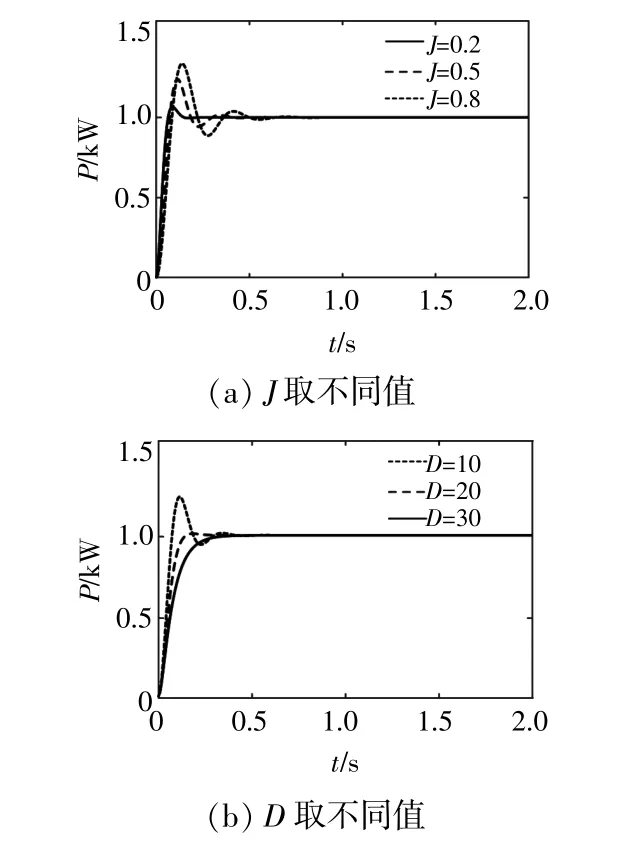
图4 有功功率阶跃响应曲线Fig.4 Step response curve of active power

由图4可知，当J增大时，有功功率的超调量增大，动态响应慢，功率变化速度相对平缓，调节时间相应变长，功率出现振荡现象，系统的稳定性受到一定的影响。当D变大时，系统阻尼增加，功率的超调量逐渐减小，动态响应慢，上升时间增大，功率波动逐渐减小，稳定性得以提高。

2.2 关键参数对输出频率的影响

根据图3可得参考有功功率Pref与输出频率ω之间的传递函数为

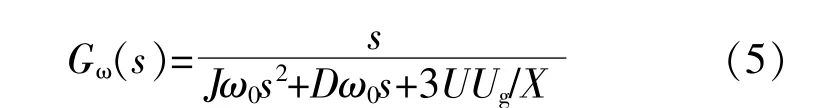
根据式（5）可得VSG输出频率的阶跃响应曲线，如图5所示。

图5 频率阶跃响应曲线Fig.5 Step response curve of frequency

由图5可知，当J增大时，VSG的输出频率变化较为平缓，响应速度变慢，可有效抑制频率突变，但同时也带来频率的振荡。当D变大时，频率的超调量减小，动态响应时间变长，可见D的增大能够有效减小频率的波动。

VSG有功环的动态性能由J和D这两个关键参数共同决定，且对输出功率和输出频率的影响又相互制约[11]。增大J可使频率变化较为平缓，但增大了功率的超调量，并且加剧了系统的振荡。减小J虽能够减弱功率的振荡，实现功率的快速响应，但会造成频率的突变，带来过大的超调。较大的D能够减小功率及频率的振荡，使之变得平缓，但削弱了系统的动态响应速度。因此，针对系统特性之间的矛盾，应综合考虑各项性能指标，折中选取J和D。

3 参数自适应控制策略

3.1 扰动状态下的功角特性

VSG功角特性曲线如图6所示。

图6 VSG功角特性曲线Fig.6 Power-Angle characteristic curve of VSG

当功率参考值从P0阶跃到P1时，系统的稳态工作点从a点变化到b点。这一变化过程并不是瞬间完成的，而是存在一个逐渐衰减的振荡过程。图7为VSG暂态振荡曲线。

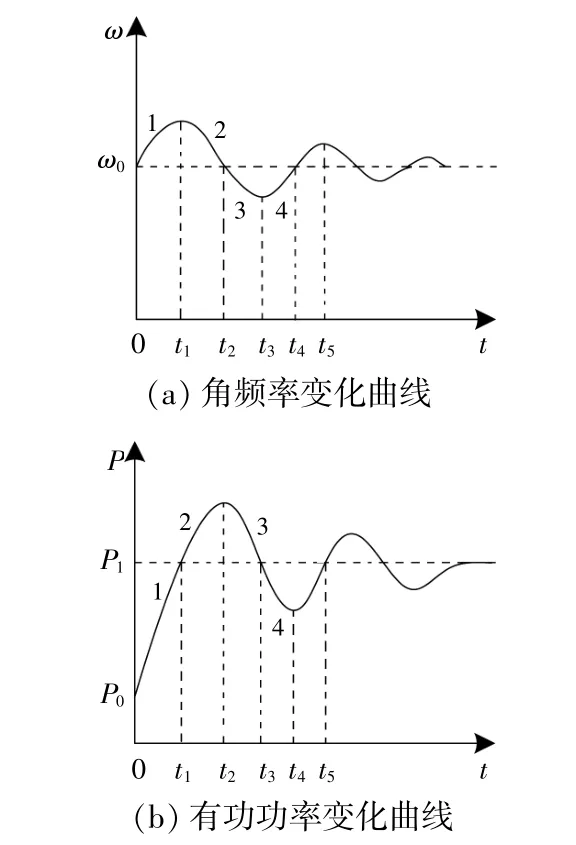
图7 VSG暂态振荡曲线Fig.7 Transient oscillation curve of VSG

当系统处于第1阶段（0～t1）时，VSG的给定功率大于输出功率，促使角频率加速增长，即dω/dt>0，且此时角频率始终大于额定值。为防止频率出现较大的超调而过多偏离额定值，应增大惯量J和阻尼D的取值，以减缓角频率的变化率及其偏移量。

当系统处于第2阶段（t1～t2）时，VSG的输出功率大于给定值，角频率到达峰值后开始向额定频率回调，该阶段的角频率仍大于额定值，但变化率始终小于0，即dω/dt<0，角频率处于减速阶段。此过程应减小惯量J以减缓功率的超调，同时可以加速角频率的回调，使其尽快回到额定值。同时在角频率偏移较大时稍微增大阻尼D，以达到进一步减小频率偏移的效果。

阶段3和阶段4的过程类似于阶段1和阶段2。由此可以根据角频率的偏差量及其变化率来分别确定惯量J和阻尼D的选取原则，如表1所示。

表1 惯量J和阻尼D的选取原则Table 1 Principles of selecting inertia J and damping D

3.2 基于模糊控制的参数自适应算法

根据表1中惯量J和阻尼D的选取原则，利用模糊控制实现上述两个参数的自适应变化，使系统具有较强的鲁棒性和自适应性。

假设VSG输出频率为ω，偏差e=ω-ω0，偏差的变化率ec=de/dt。将连续域的e和ec转换成离散域N=[-n，-n+1，…，-1，0，1，…，n-1，n]，n为离散量的档数，本文取n=6。设在连续域内输入量的取值范围为[xL，xH]，则转换到离散域的量化因子可以表示为

式中：x为连续域的e或ec；X为离散论域E或Ec。

将得到的模糊语言变量进行区间划分，分别记为：{PL，PS，ZE，NS，NL}。其中，PL和PS分别代表偏离正方向较大和较小的数值；ZE表示没有偏差；NS，NL分别代表偏离负方向较小和较大的数值。考虑到频率偏差量E过0时有较高的区分度，此处选择三角形隶属度函数，其他位置均选用较为平滑的高斯型隶属度函数。

输入值的隶属度函数如图8所示。根据表1中参数的选取原则，制定模糊控制规则，如表2，3所示。

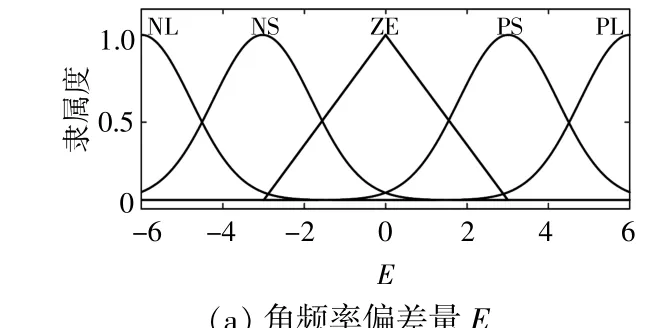
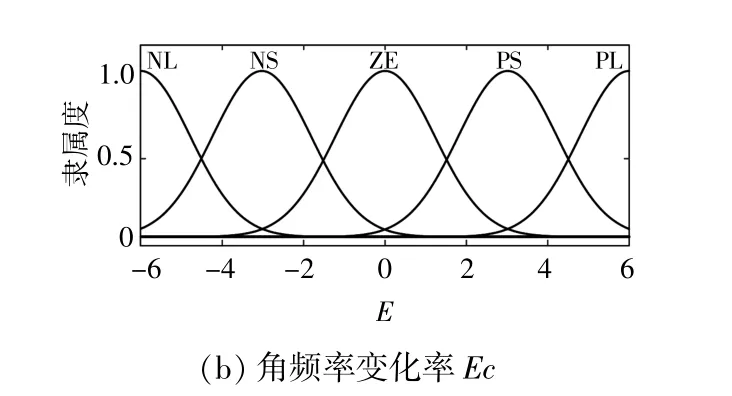
图8 输入量的隶属度函数Fig.8 Membership function of the input

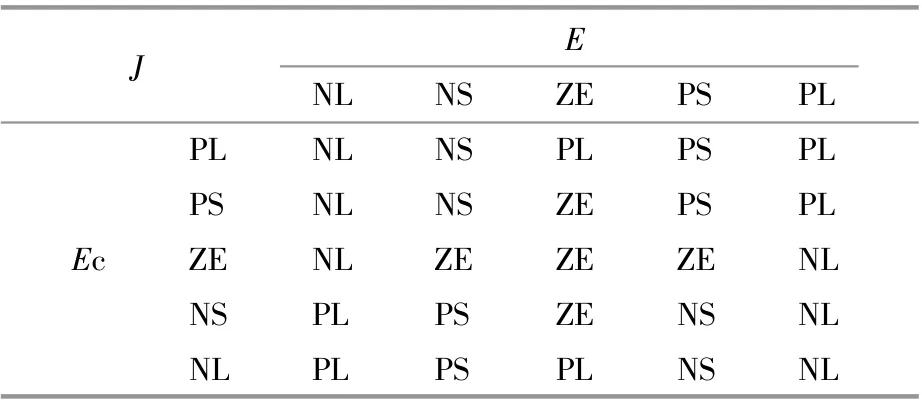
表2 惯量J的模糊控制规则表Table 2 Fuzzy control rule of inertia J

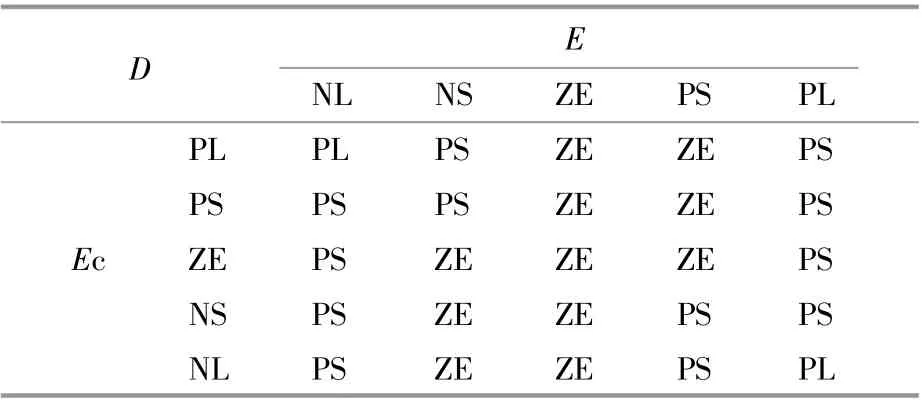
表3 阻尼D的模糊控制规则表Table 3 Fuzzy control rule of damping D

模糊控制下J的输出呈现双向发展，变化灵活，可设置大的初始惯量来抑制频率的波动；D的输出变化较为平缓，避免了阻尼过大而造成的响应缓慢的问题。由此可得输出量的模糊集合，输出量选择适用性强、计算简单的三角形隶属度函数，如图9所示，利用重心法，对输出模糊集合求取加权平均值，论域仍为[-6，6]，得到最终输出量U。

图9 输出量的隶属度函数Fig.9 Membership function of the output

设自适应参数的调节范围为[yL，yH]，将最终的模糊输出量U转换到连续域下的量化系数为

自适应参数y的输出表达式为

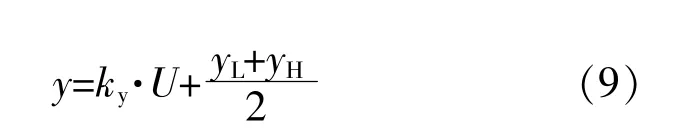
式中：y为惯量J或阻尼D的自适应变化取值。

根据前文分析，可得基于模糊控制的惯量J和阻尼D的自适应控制框图，如图10所示。

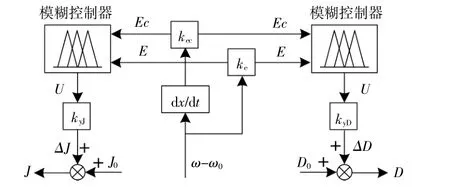
图10 基于模糊控制的自适应控制框图Fig.10 Adaptive control diagram based on fuzzy control

4 仿真与实验验证

4.1 仿真验证

为验证基于模糊控制的参数自适应算法的可行性，在Simulink中搭建VSG模型进行仿真分析，仿真参数如表4所示。

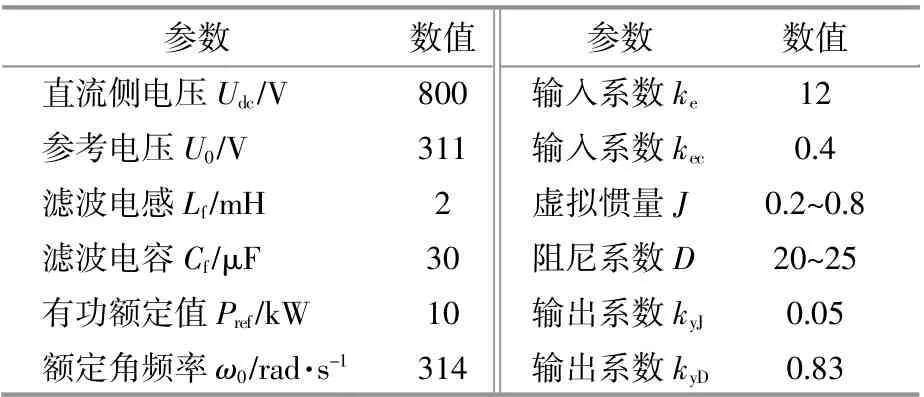
表4 仿真参数Table 4 Simulation parameters

仿真工况为VSG并网运行，启动时有功参考值为5 kW，2 s突增到10 kW，4.5 s再降为5 kW。对固定参数控制和参数自适应控制两种方式进行对比仿真，结果如图11，12所示。

图11 不同控制方式下的有功功率波形Fig.11 Active power waveforms under different controls

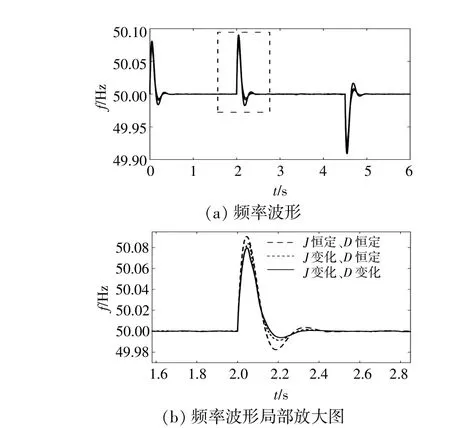
图12 不同控制方式下的频率波形Fig.12 Frequency waveforms under different controls

由图11，12可得，参数固定不变时，有功和频率均具有较大的超调，调节时间较长，系统有较大波动；仅采用惯量J自适应控制时，系统超调量降低，调节时间变短，系统波动得到抑制；采用惯量J和阻尼D双参数自适应控制时，控制效果得到了进一步提高，验证了基于模糊控制的参数自适应控制策略的有效性。

图13为模糊控制自适应参数J和D的变化情况。

图13 模糊控制自适应参数的变化Fig.13 Variation of adaptive parameters when fuzzy control is used

由图13可以看出，参数J和D均连续变化，J以初始值为中心呈双向变化，D的变化范围相对较小，以免阻尼过大而减缓响应。系统发生振荡时，J和D均增大，从而减小波动带来的影响；频率恢复时，J和D均减小以加快该过程。

4.2 实验验证

在基于TMS320F28335的LC型并网逆变器平台上对参数自适应控制进行实验验证。t0时刻有功功率参考值增加1.5 kW，t1时刻减少0.75 kW，实验结果如图14所示。

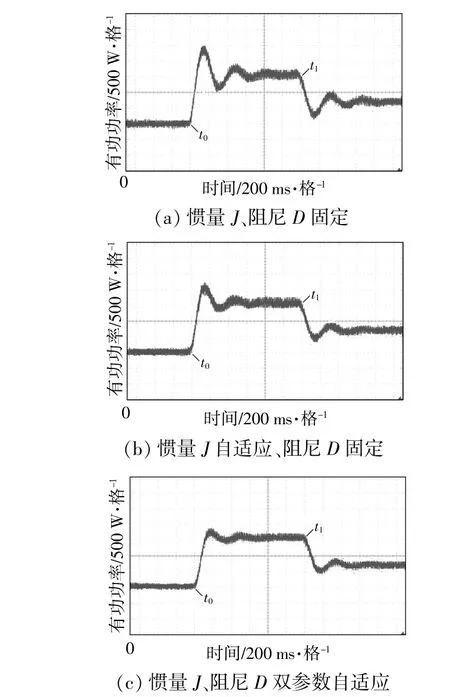
图14 不同控制方式下的有功功率波形Fig.14 Active power waveforms under different controls

由图14可以看出，采用惯量J的自适应控制要比固定参数控制的功率变化更为平缓，而采用惯量J和阻尼D双参数自适应控制的动态性能又优于前两种控制方式，其超调更小，调节时间更短，有效抑制了有功功率波动。

5 结论

针对传统虚拟同步发电机固定参数无法兼顾快速性和稳定性的特点，本文建立其数学模型，分析了转动惯量和阻尼系数对虚拟同步发电机特性的影响。从功角特性出发，确定转动惯量和阻尼系数的选取原则，进而提出一种基于模糊控制的虚拟同步发电机参数自适应控制策略，兼顾了系统动态调节的快速性和稳定性，同时增强了系统的鲁棒性。通过与传统固定参数控制策略的对比仿真和实验，验证了所提控制策略的可行性和有效性。