明渠平板闸门过闸流量特性研究

申祖宁，张文正，姜明梁，吕谋超

（1.华北水利水电大学水利学院，郑州450046；2.中国农业科学院农田灌溉研究所/农业农村部节水灌溉工程重点实验室，河南新乡453002）

0 引 言

我国水资源分布极不均匀，总体表现为南多北少、北方干旱少雨，严重制约了工农业的发展，这就要求我们更加合理地利用和分配水资源[1]。我国共有大中型灌区7 800 余处，部分灌区仍存在工程老化、配套设施不完善、信息化水平较低等问题，难以支撑起当地农业和经济可持续发展。“十四五”期间，国务院将大型灌区续建配套与现代化改造纳入了近期推进的150项重大水利工程，进一步加强大中型灌区建设与管理[2]。灌区续建配套了许多水利工程、量配水设施及水利信息化工程，其中量配水设施是支撑灌区现代化发展、提高水资源利用效率的关键技术，是提升灌区用水管理水平、核定水费、推进农业水价综合改革的重要保障。

配套完善用水计量设施并推广应用，提升灌区水资源管理能力，是大型灌区续建配套与现代化改造中的重要环节。胡荣祥等[3]对量水设施率定方法进行了分析研究，给出了不同输水方式对应的不同率定方法。管光华等[4]提出了一种用于灌区实际应用的率定模型，且大部分数据的误差保持在5%以内；孔祥宇等[5]通过改进的人工蜂群算法降低了闸门实际流量与给定流量的差值。邓海龙等[6]将渠道量控一体化系统在江西省赣抚平原灌区二干渠灌片进行了应用，其效益效果提升较为明显；赵万勇等[7]运用FLUENT 数值模拟对明渠平板闸门淹没出流流场进行研究，通过与实测流量的对比验证了数值模拟的可靠性；高军等[8]研发了一款智能测控一体化闸门装置，可进行远程自动灌溉控制和调节，解决了渠道末端控制问题。Dou 等[9]以水闸为例，建立了基于人工神经网络和回归分析的自由流计算模型，并利用实测数据对模型进行了充分验证。实验结果表明，三阶多项式和多层感知器神经网络具有较好的适应性。

近年来对闸门量水的研究越来越多，但末级渠系的量水精度和信息化程度还处于较低水平。目前灌区平板闸门主要通过测量闸门前后水位及闸门开度来计算流量，以此实现灌区闸门测控一体化，提高灌区的信息化水平。平板闸门在灌区中应用较为广泛，为保证闸门测流的精度，对流量系数经验公式的选取就显得尤为重要。对此，国内外学者也进行了大量试验研究，依据不同的适用条件得到了多种流量系数经验公式[10-14]。

本文基于室内水力学性能试验，依据最小二乘法原理拟合出闸孔自由出流状态下的流量系数公式，并与3种常用的闸孔自由出流流量系数经验公式：Garbrecht[10]公式、杜屿[11]公式、武汉水利学院[12]公式进行对比分析，研究发现通过本试验拟合公式的适应性更好，流量计算精度更高，可为渠道平板闸门量控水技术研究提供理论基础。

1 平板闸门测流原理

矩形平板闸门因体积小、安装方便、性价比高、驱动能耗低等特点，被广泛应用在灌区斗农渠中[15]。根据明渠测流理论，矩形平板闸门通过闸门开度变化来调节流量，当闸门开度与闸前水位之比e/H0≤0.65 时，属于闸孔出流状态。根据闸门下游水位的影响效果，闸孔出流又可分为自由出流和淹没出流，若闸门下游水位不影响闸下流出的射流状态，称之为自由出流；反之，则称为淹没出流。本文主要针对闸孔自由出流状态展开研究，如图1 所示[16]，H为闸门上游水位，Ht为闸门下游水位，e为闸门开度，H0为包含水动能的闸前总水头，在实际应用中常忽略动水位，用H代替H0。

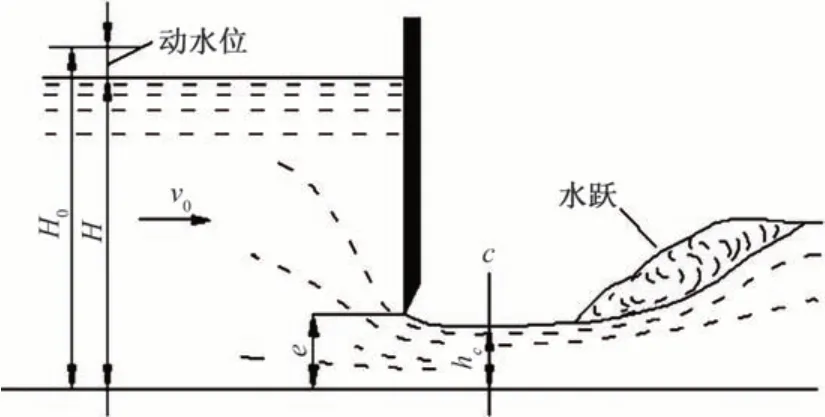
图1 闸孔自由出流Fig.1 Sluice free outflow

闸孔自由出流状态的过闸流量计算公式为：

式中：μ0为孔流流量系数；b为闸门宽度；e为闸门开度。

闸孔自由出流流量计算值的不同主要在于流量系数选取的不同[14]，而流量系数的选取同样决定计算值的精确度。以下为3种常用的闸孔出流流量系数经验公式。

（1）Garbrecht公式：

（2）杜屿公式：

（3）武汉水利学院公式：

流量系数μ0一般与闸门相对开度（e/H0）有关[17]，而流量系数μ0是闸门开度、闸前水位的函数，也可通过试验装置来控制流量Q、闸门开度e，获取闸前水位H0等参数，利用闸孔自由出流流量公式反推出流量系数μ0：

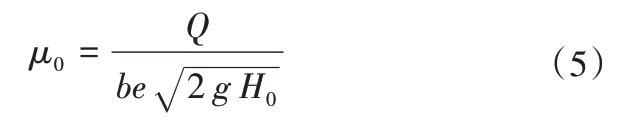
本研究设置不同试验工况，测出多组流量系数μ、e/H0的值，从而获得μ0与e/H0的相关关系，并与3种常用经验公式的函数图像进行对比，依据最小二乘法拟合出新的流量系数公式，并验证其可靠性。

2 试验设计

试验布置于中国农业科学院农田灌溉研究所的渠道水力学性能测试平台，试验渠道为矩形钢化玻璃材质，宽60 cm，深58 cm，底坡斜率i为0.005 24。渠道前段设有蓄水池、消力池、水泵等装置，可通过变频控制柜调节水泵，进而控制流量，使蓄水池水位升高，水流自然进入渠道（见图2）。为减轻紊流对闸门测流的影响，在距离消力池15 m 处的渠道中布置了测控一体化矩形平板闸门，闸门过水宽度为60 cm，开度启闭精度为1 mm，可通过远程自动调节和现场手动调节两种模式来控制闸门启闭高度。渠道末端设有挡水板和回水装置，通过调节挡水板可控制下游水位，通过调节开度使其保持在闸孔自由出流的状态，渠道的水通过回水装置流回蓄水池，可循环使用。

图2 试验布置示意图Fig.2 Schematic diagram of test layout

矩形平板闸门开度最小设置为3 cm，根据不同工况依次抬升1 cm，并使闸门开度与上游水位的比值始终不大于0.65。闸门上游水位通过液位计量测，测量精度为0.1 mm。渠道过水流量范围为100～200 m3/h，梯度为20 m3/h。充分考虑渠道特点、水流流态等情况，共进行17组不同工况试验。

3 结果与分析

3.1 试验结果与3种经验公式对比分析

为能直观的表现试验的实测数据与3种流量系数经验公式两者之间的数值关系，将试验实测数据代入闸孔自由出流公式（1），得出闸门相对开度e/H0和闸孔自由出流流量系数μ，见表1。

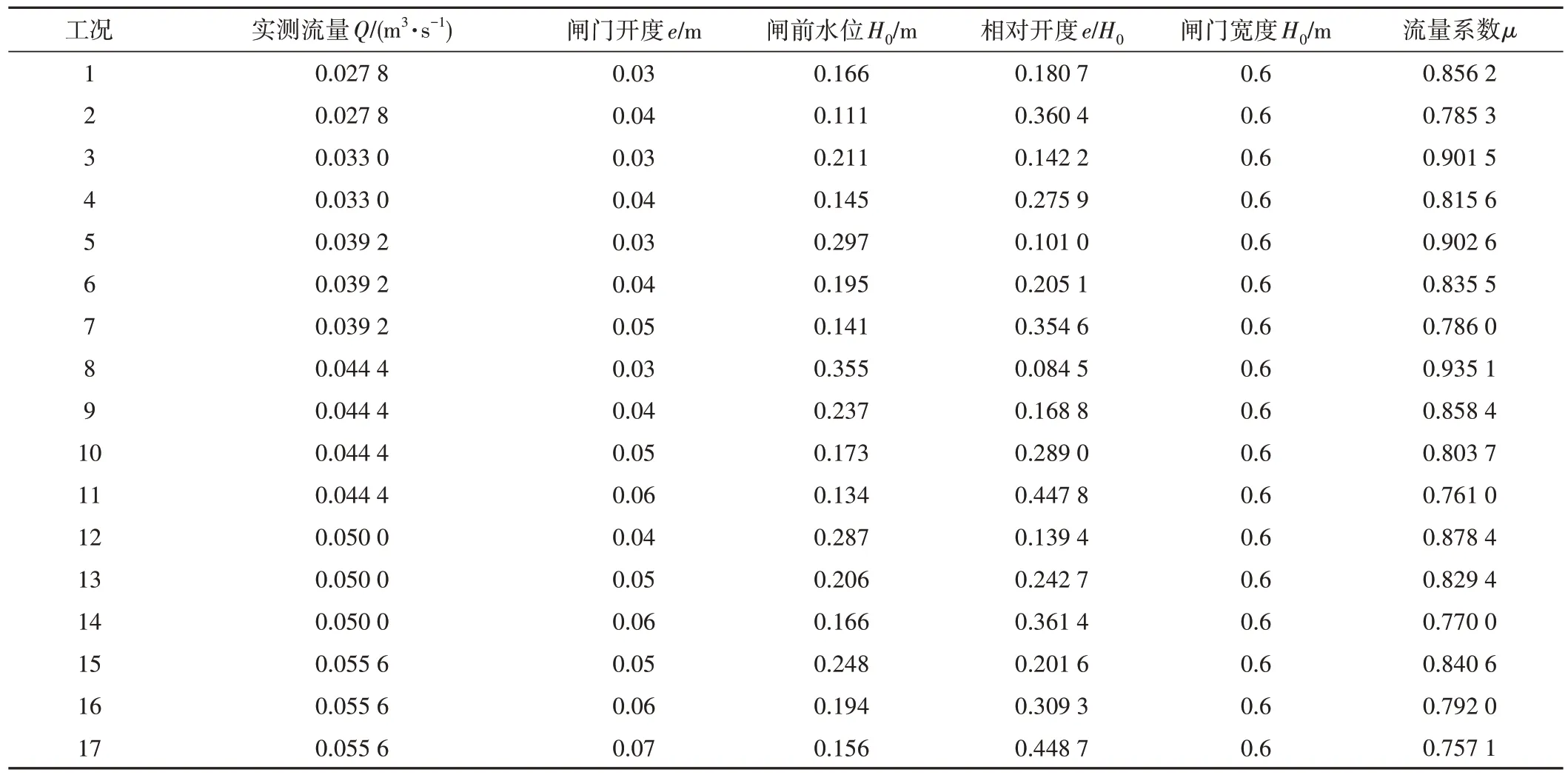
表1 试验数据与计算数据Tab.1 Test data and calculation data

将所得的（e/H0，μ）各点分别与Garbrecht、杜屿、武汉水利学院3种流量系数经验公式的函数图像进行比较，对比结果见图3～图5。

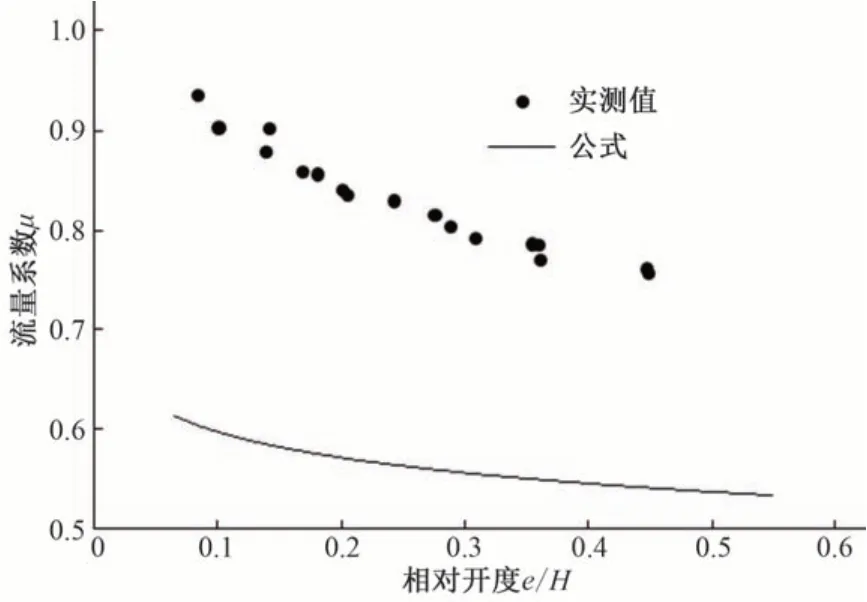
图3 Garbrecht公式Fig.3 Garbrecht formula

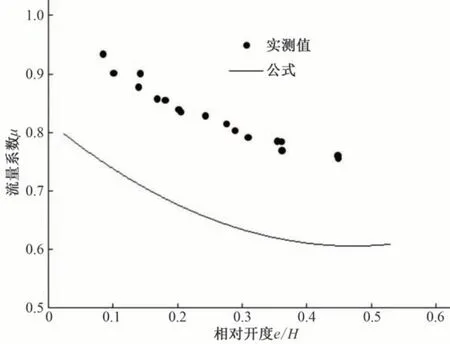
图4 杜屿公式Fig.4 Du Yu formula

由图3～图5 可知，武汉水利学院公式中的μ0与e/H0呈线性关系，与实测的μ0与e/H0的对应关系显然不符，且误差较大。Garbrecht 公式、杜屿公式的趋势线同实测值的趋势较为相似，而杜屿公式的相似度更高。

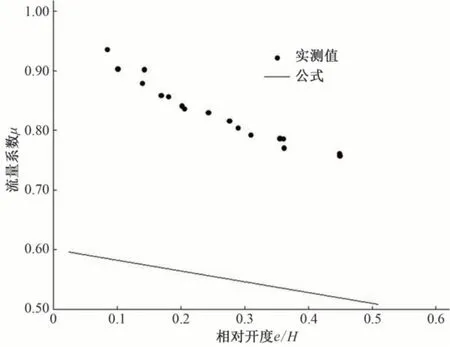
图5 武汉水利学院公式Fig.5 Formula of Wuhan University of water conservancy

通过计算可知，Garbrecht 公式、杜屿公式、武汉水利学院公式流量计算与实测值的最大绝对误差分别为0.017 7、0.011 3、0.018 3 m3/s，绝对误差平均值分别为0.013 6、0.008 6、0.014 2 m3/s。3种经验公式计算的过闸流量相对误差值见图6。由图6 可知，武汉水利学院公式和Garbrecht 公式的相对误差值均较大，误差范围在30%～40%之间，其中武汉水利学院公式在工况8 条件下最大相对误差为37.46%，而杜屿公式误差在20%处浮动，相对另外两种经验公式来说误差较小。

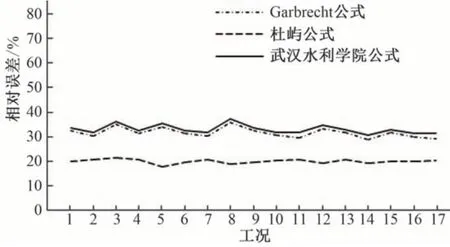
图6 各公式计算结果相对误差比较Fig.6 Relative error comparison of each formula computing results

3.2 反推流量系数及结果分析

根据函数图像特点，采用最小二乘法原理将实测数据计算值（e/H0，μ）各点输入拟合程序，并进行不同关系的拟合，选取其中拟合效果较好的二次多项式曲线，即流量系数μ0值近似采用如下公式表示：

式中：A、B、C均为常数。

A、B、C的值可由最小二乘法进行回归拟合后求出，最终得到拟合方程为：

其曲线相关性为0.978 2，拟合精度很高，满足拟合要求，见图7。

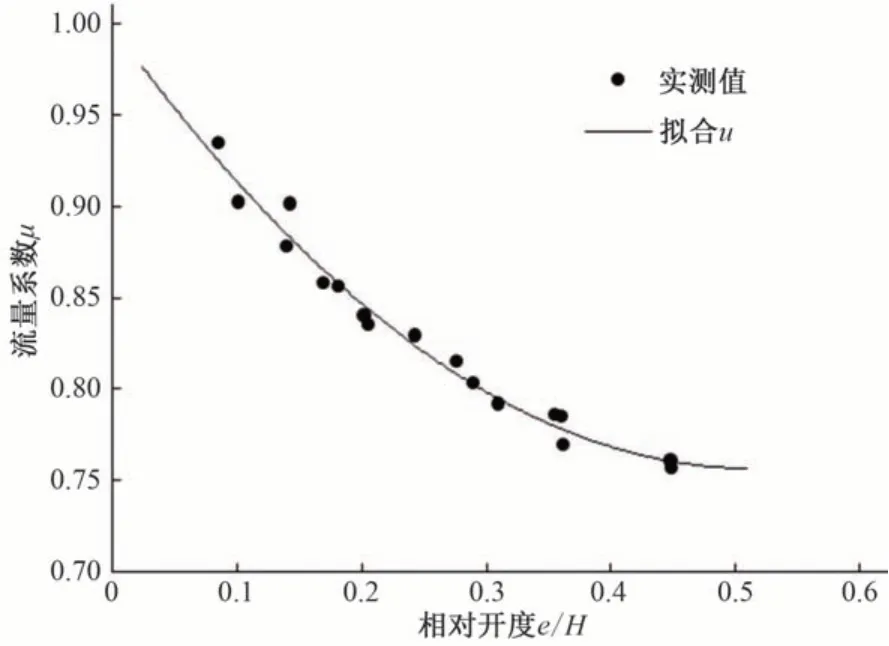
图7 拟合公式Fig.7 Fitting formula

为进一步验证流量系数拟合公式（8）的流量计算值与试验实测流量值的吻合性，另选取17 组工况将计算流量与实测过闸流量进行对比，并计算相对误差，由表2可见，自由出流条件下，计算流量与实测过闸流量的相对误差平均值为1.68%，根据《GB/T 21303-2017 灌溉渠道系统量水规范》规定，新拟合公式满足渠道量水的精度要求。

表2 流量系数分析结果Tab.2 Analysis results of discharge coefficient

将3种常用流量系数经验公式与新拟合出的流量系数计算公式（8）的适用性进行对比分析，采用相对误差最大值（Rmax）、相对误差平均值（Rave）、变差系数（Cv）来分析各公式流量计算值的精度。各公式计算的Rmax、Rave、Cv值见表3。

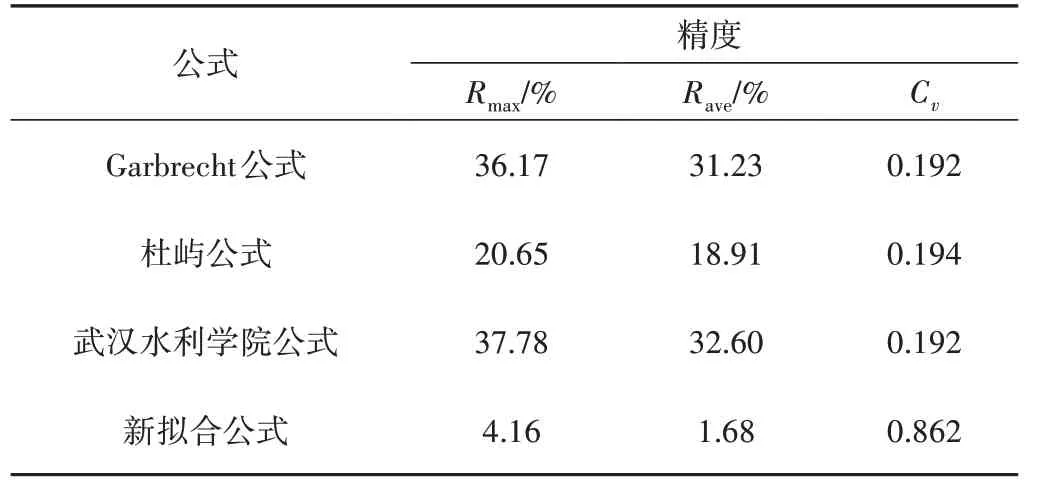
表3 各公式计算的Rmax、Rave、Cv值Tab.3 Rmax、Rave and Cv value of each formula

由表3可知，①Garbrecht公式和武汉水利学院公式求得的Rmax较为接近，且武汉水利学院公式求得的Rmax最大，为37.78%，杜屿公式求得的Rmax为20.65%，比前两者较小，新拟合公式的Rmax最小，为4.16%。②新拟合公式求得的Rave最小，为1.68%，其次是杜屿公式，为18.91%，Garbrecht 公式和武汉水利学院公式的Rave值最大，分别为31.23%、32.60%。③从变差系数Cv来看，Garbrecht 公式、杜屿公式和时武汉水利学院公式的值比较近似，分别为0.192、0.194 和0.192，新拟合公式的Cv值为0.862，虽然不是最小，但相差不大，说明其离散程度和误差波动都较小。

综合考虑绝对误差值、相对误差最大值（Rmax）、相对误差平均值（Rave）和变差系数（Cv）变化情况，可见新拟合公式的效果较好，相对误差小，更适用于矩形斗农渠道的用水计量。

4 结 论

本文利用渠道室内试验平台，布置测控一体化矩形平板闸门，对闸孔自由出流条件下流量系数公式选取进行了分析研究，得到以下结论：

（1）探讨了Garbrecht 公式、杜屿公式、武汉水利学院公式对矩形渠道的适用性，通过3种经验公式的过闸流量计算值和实测值的对比，发现误差较大。

（2）通过控制过闸流量、实测闸门开度和上游水位等数据反推出流量系数μ0，利用最小二乘法原理将各个实测计算值通过拟合程序拟合出新的流量系数公式，显示曲线相关性较高，说明拟合精度较好、满足拟合要求。

（3）通过新拟合的流量系数公式分析计算流量与实测流量的绝对误差、相对误差和变差系数，与其他3种公式进行比较，相对误差均值仅为1.68%，且相对误差都在5%以内，可知利用最小二乘法拟合的公式适用性更好、精度更高。

本文是在室内利用玻璃材质渠道进行试验的，与田间实际应用条件还存在一定差异，未来尚需将闸门安装在田间典型斗农渠中进行实际水力学特性测试研究。