灌区明渠糙率及其计算方法
卫小丽,章少辉,2,白美健,2
(1.中国水利水电科学研究院,北京100038;2.流域水循环模拟与调控国家重点实验室,北京100038)
0 引 言
灌区用水过程的重要载体是明渠,其主要物理参数是糙率[1]。明渠糙率的物理意义是各类因素对水流运动阻力的定量表征[2]。对灌区明渠水流而言,在均匀流、恒定非均匀流、甚至完全非恒定流态下,如何计算获取准确的糙率值,是合理设计输配水及排水工程、开展灌区水动力多过程模拟仿真工作、提升灌区整体用水质量、实现灌区智慧化管理的重要前提。
明渠糙率取值应区分两种典型工况,一是工程设计阶段的糙率,即设计工况取值,二是工程实际运行时的糙率,即实际工况取值。这两类糙率取值,事实上都是基于实测数据计算得到,因为糙率本身并不是一个物理可观测量[3]。对设计工况值而言,由于没有对应的实际工程数据可观测,故只能借助已有公式、采用类似物理条件的实验室装置或其他类似状况的原型工程实测值来反向计算糙率值。而实际工况下的流态具有显著的复杂多样性,难以严格达到糙率定义满足的均匀或拟均匀流态,故实际工况的糙率在空间平均的基础上,应是一个时均流态值[4],这与热力学中均衡和非均衡系统之间的关系类似[5]。由此,导致了不同工况下丰富多彩的糙率计算方法。
本文在回顾糙率的定量表征发展史基础上,阐明了糙率的影响要素,总结了糙率计算的主要方法及其优缺点,讨论了在当前各类技术快速发展的背景下糙率计算方法的发展趋势,以期为实际工作中获得更加合理准确的糙率值提供一些扩展思路。
1 糙率表征回顾
糙率的概念源于对水流运动的能量耗散描述,具体而言,就是对渠道水流所受阻力的定量表征[2]。从历史视角而言,为合理的设计引水明渠横断面几何尺寸及坡度,法国水力学家谢才基于均匀流情景下水流重力与阻力相等的观察认知,通过假设水流阻力与渠道平均流速的平方和湿周分别成正比的前提条件,于1769年提出一个半理论公式,并通过均匀流观测试验数据,验证了该公式的合理性[2]。为增强其实用性,谢才对其进一步简化后,于1776年获得了迄今被广泛应用的表达形式[3]:

式中:V为通过渠道横断面的平均流速,m/s;R为水力半径,m;J为水力梯度或比降,m/m;C为谢才系数,m1/2/s。
在历史上,有一个与谢才公式(1)类似的公式,即Darcy-Bazin 公式,是法国水力学家达西和其助手巴辛通过大量室内实验总结的统计分析结果,其形式表达如下[6]:

式中:a和b为两个待定参数。通过类比式(1)和式(2)可知,式(2)等号右侧括号内的变量,即是C2。
把谢才公式(1)应用于实际工程问题的重要前提工作,就是确定谢才系数C的具体数值或包含水力梯度及水力半径等可观测量的解析函数表达式。19 世纪上半叶,通常认为谢才系数为常数,因为这更利于当时无复杂计算工具的工程师们做简单运算[7]。然而,随着工程案例的增多,人们发现这难以与实测结果相吻合。为此,瑞士学者Ganguillet 和Kutter 于1869年首次引入了糙率系数的概念,给出了C的一个解析计算式[6]:
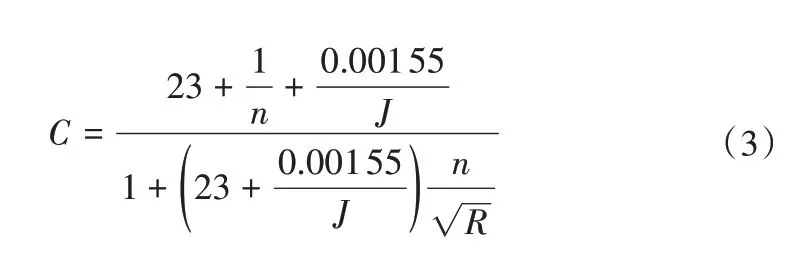
虽然从物理学视角而言式(3)存在着量纲不协调的怪异问题,但该公式发表后以其计算简单的显著优势而迅速被欧美水利工程师们所接受,并累积了大量不同材料衬砌下糙率系数取值表。工程计算永远追求简洁高效实用。为此,著名法国水力学家曼宁,在式(1)和式(3)的基础上,于1890年总结发表了一个形式更为简洁的流速计算经验公式[2]:

式中:c为流动阻力系数,m1/3/s。
如果与目前被广泛应用的如下公式做对比,即可知流动阻力系数c与糙率系数n成反比[3]:

若联立求解式(1)和式(5),即可获得如下教科书中被广泛载录的曼宁公式[8]:

直接基于式(6)进行推导可知,糙率系数的单位为s/m1/3,很多文献中的公式推导,均采用该奇特的量纲。糙率系数另一个常用的量纲形式更加简洁,在国际单位制下直接取m1/6[9],比如美国土木工程师协会(ASCE)推荐的手册[10],这是因为在式(6)中引入了一个具有国际单位制(m1/2/s)的单位系数cu,此时式(6)被表达如下,这就是曼宁公式量纲不协调的问题。

自从Ganguillet 和Kutter 提出糙率系数的概念后,其在不同工况下的累计值日益剧增,且通过查询表格的手段获得对应的糙率值后,式(4)或式(5)可满足一般的工程设计要求。因此,虽然其缺乏理论基础,且量纲不协调,但简洁实用的形式及计算流程,使曼宁公式成为了水力学中应用最为广泛的公式之一[3]。
由上所述,糙率事实上源于均匀流下经典的明渠过流能力设计问题,从经验的视角定量描述了明渠水流运动这个物理耗散系统的能量耗散特征。从拉格朗日视角而言,这个能量耗散源于水流粒子之间相互碰撞形成的阻力以及水流粒子与各类其他物体粒子之间的摩擦力[11]。
对于明渠非恒定流而言,由于目前没有更好的描述水流阻力的方法,故仍沿用糙率的概念进行描述[12]。因此,式(5)目前已经被广泛引入圣维南方程组或地表浅水方程组中,以定量表征非恒定水流受到的空间诸点的时均摩阻力,并取得了较好的模拟效果,此时的糙率即是空间诸点的时均糙率。以圣维南方程组为例,在适合于数值计算的守恒形式下,地表水摩阻力Sf被表达如下[13]:

相应的圣维南方程组的动量守恒分量式表达如下[14]:
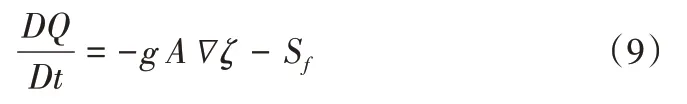
式中:Q为明渠流量,m3/s;为流量Q的拉格朗日全微分算子;A为过流断面面积,m2;g为重力加速度,m2/s;ζ为地表水位,m;∇为空间梯度算子。
对于正在输配水或排水的明渠而言,水流流态更接近恒定非均匀流,此时可忽略式(9)中左侧的时间变化率项,从而在实际观测渠段可获得沿渠长方向的空间平均糙率值,或称之为沿程糙率。如果分别用变量下标“in”和“out”标记观测渠段的入流和出流位置,则在恒定非均匀流状况下,由式(9)可直接获得如下沿程糙率的表达式,是当前常用的糙率计算公式[15,16]:
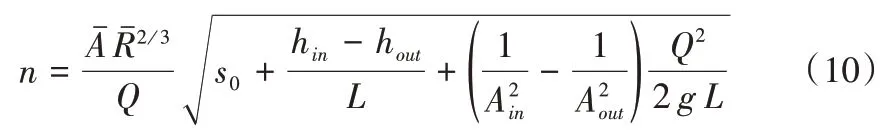
式中:L为观测渠段的长度,m;s0为渠底坡度,m/m;变量上侧的符号“—”表示观测渠段入流和出流位置的水力学变量的算术平均值。
2 糙率影响要素
如前所述,糙率是对明渠水流所受阻力的定量表征。由于实际工程中形成阻力的因素众多,故难以对糙率进行理论推导和表征,这也是上述各类糙率表征式仅是经验公式的缘由。由于影响明渠水流运动阻力的要素众多,故捋清并分类相关影响要素,是获取合理糙率值、分析误差来源、形成新型糙率计算方法的基本前提。
2.1 工程要素
从式(5)所包含的变量而言,凡是能影响观测区域内水力梯度J、过流断面A及湿周χ(R=A χ)的工程要素,均能影响糙率值。故从直观而言,糙率影响要素包括:渠道断面尺寸、壁面粗糙度、水工建筑物形式、渠道平顺情况、渠底比降、渠道淤积、悬浮泥沙、渠内杂草植被、渠道水深、施工质量、使用年限以及运行维护条件等[17-22]。这也表明,灌区明渠进行定时清淤,定期维护,是减少糙率不确定性、提高输配水和排水效率的重要前提[23]。
上述工程要素虽然众多,但它们在一定程度上相互依存、互相作用。以明渠内植被覆盖的情况为例,在不同植被覆盖度下,糙率与度量湍流度的雷诺数、水深以及坡度均有关系,且对应关系相对而言较为复杂。当植被覆盖率大于一定值时,糙率及糙率变化率均随雷诺数的增加而增大。另当植被覆盖度大于某值时,糙率则随着水深的增加呈幂函数递增趋势。在一定坡度下,糙率随着植被覆盖度的增加而增加[24,25]。针对植被的各项因素,譬如植被密度及植株高度对糙率的影响,也进行了大量详细的实验研究。研究结果表明:同一流量下,糙率随植被密度和植株高度的增加而增大;且相同条件下,植株高度对水流的阻力作用要高于植被密度的阻力作用[26]。除此之外,白寅祯等[27]使用winSRFR 软件对春小麦不同生育期(依次为分蘖期、拔节期、孕穗期及灌浆期)的畦田糙率进行研究,指出田面糙率总体表现为灌浆期>分蘖期>孕穗期>拔节期,究其原因,其一为作物长势越茂盛对水流推进的阻碍作用越明显,进而导致田面糙率越大;其二,由于分蘖期土壤结构松散、田面起伏不平,导致水流推进阻碍较大,故该生育期阶段作物长势虽最不茂盛,但田面糙率却并非最小。
如果明渠中存在泥沙,比如引黄灌区输配水渠道,需考虑泥沙对糙率值的影响[28]。目前对含沙量的影响进行分析时存在某些分歧,有人认为含沙量影响的是水流内部的内能消耗,对糙率没有影响[18],有人则认为以悬移质泥沙为主的挟沙水流中泥沙的存在使水流紊动受到阻碍,进而减小糙率[29]。这两者出现分歧的起点是对于糙率的定义有所不同,前者将糙率简单定义为边壁对水流的阻碍作用,后者则将其定义为综合糙率,水流内部消耗也被视为糙率的一部分。
2.2 物理要素
若从水流的物理状态而言,以平均流速和浅水波速之间的比值定义的傅汝德数[30],显然直接影响着糙率值,因为傅汝德数直接决定了明渠水波的扩散方向及其非线性叠加耦合过程,从而直接影响决定了水流的湍流度、过流断面及湿周形态[2],实测结果亦表明,无论急流还是缓流,傅汝德数都与糙率有着极为明显的线性或非线性函数关系[16]。实测结果表明[28],水位较低时,糙率与平均水深的相关程度较高,平均水深越低,糙率相对越大。
对非恒定流而言,若把曼宁糙率式(5)融入到圣维南方程组或地表浅水方程组中后,糙率值就会与水动力过程耦合[31]。此时,基于实测值,直接用式(5)计算获得的时均糙率值,比融合水动力学方程后的时均糙率值大近50%,原因是水动力过程具有显著的自我非线性对流输运特征[32]。从非平衡态物理及糙率是描述水流阻力这两个视角而言[14],考虑水动力过程后的时均糙率值,显然更能反映真实的物理现象。
另外需注意的是,上述工程要素中提到了悬浮泥沙对糙率的影响。若从物理流态而言,在相同试验装置和流量条件下,水沙两相流的湍流过程会显著不同于单纯的水流过程[33]。而正如上述所言,水流阻力的一个重要来源就是湍流状况下水流粒子之间不同程度的相互碰撞导致的局部能量耗散,这种能量耗散会引起极其直观的流速分布变异[34],进而导致不同程度的阻力。故从物理机理而言,水中存在悬浮泥沙应会影响到糙率取值。
3 糙率计算方法
糙率是一个不可直接观测的物理变量,故基于实测数据进行反向计算是最基本的获取糙率值的手段。实测数据源于两种方式,一是室内严格的物理实验,二是工程原型观测,由于两者有时相差较大,故后者更具备实际工程意义。由此,形成了基于原型观测试验的最基本的糙率计算方法。进而,通过把基本的糙率公式融入水动力学方程组中,使得糙率更加接近水流所受真实阻力的表征。在此基础上,形成了数值求解水动力学方程的同时,借助智能优化算法或数据同化算法,迭代反算糙率的方法。
3.1 原型观测方法
随着实际工程案例的增多,采用原型观测数据来反向计算糙率,逐渐成为扩充糙率推荐值的重要手段。例如,曾祥等[35]依据实测资料以及各地糙率设计取值,结合有关设计手册,针对不同地区和不同衬砌方式的混凝土渠道,列出了混凝土渠道糙率值推荐表,指出大型混凝土渠道糙率介于0.015~0.018 之间,均匀段糙率则介于0.011~0.013 之间。王开等[36]在整合国内外大型灌溉工程糙率取值基础上,指出良好衬砌状况下灌溉明渠糙率介于0.014~0.015 之间、非灌溉明渠糙率介于0.011~0.013 之间,该差异与施工质量密切相关;针对南水北调中线工程,结合设计规范和工程经验选取糙率值为0.015,且在此基础上,建立了长距离渠道输水能力校核模型,分析结果表明:糙率在一定范围内每增加0.001,渠道水面线抬高幅度约为0.2 m。王光谦等[29]通过对国内外渠道糙率取值的分析以及输水渠道实地考察,结合设计规范与经验确定南水北调中线渠道糙率基准值为0.013,在此基础上引入不同因素的影响因子,得到中线工程明渠段糙率取值为0.015,并针对设计流量及加大流量,确定了其在不同运行阶段的糙率值。目前已有大量此类相关文献,此处不再做更多综述,文献中这些由原型试验总结而来的糙率值,在明渠工程设计和灌区用水管理中,起到了重要的基础数据支撑作用。
然而,该类方法的缺点是受随机因素影响较大,随机因素包括渠道沿程高度及横断面几何尺寸测量误差,以及流量和水位测量误差等。为定量描述随机因素带来的糙率不确定性,杨开林和汪易森[15,37]以及郭新蕾等[16]理论推导出渠道糙率率定误差与水力测量(水位与流量)误差之间的定量关系,并进行了多个渠道原型观测和理论分析。结果表明,糙率率定误差与流量测量误差基本相同;糙率的进出口水深误差绝对值非常接近;渠道越短,糙率的水深误差就越大。为减小糙率误差,即提高糙率率定精度,郭新蕾等[16]在系统研究测量水位误差、渠道长度和渠道雍水对糙率精度的影响后,建立了计算渠道糙率率定误差的简化公式,并针对以上影响提出了减小糙率误差的方法:①使渠道进出口位置的观测水位具有同方向误差;②合理布设渠道测点,使渠道长度满足设定条件;③控制闸门开度来减小渠道中雍水坡度[16]。
原型观测试验是一切计算糙率工作的基础,更合理与完善的糙率计算方法,均需基于原型观测数据。故对相关研究与应用而言,加大原型试验观测力度和广度,是提高一切糙率研究工作质量的基础。
3.2 系统辨识方法
系统辨识方法是现代控制理论的一个分支,借助可观测输入和输出数据,依据最小二乘法或变分法等寻优方法来率定黑箱模型中的待定系数,达到预测当前问题合理参数的目的。在水利工程中引入此类方法的目的,是减弱原型观测试验方法带来的随机因素影响程度。
对明渠沿程糙率而言,存在如下经验表达式[16]:
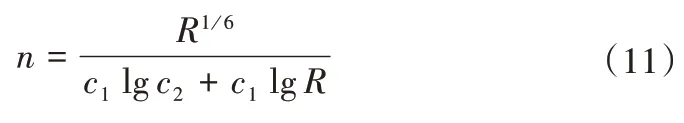
式(11)实际上是在大量原型观测数据基础上,由式(10)进一步简化得到的如下两式总结而来[16]:
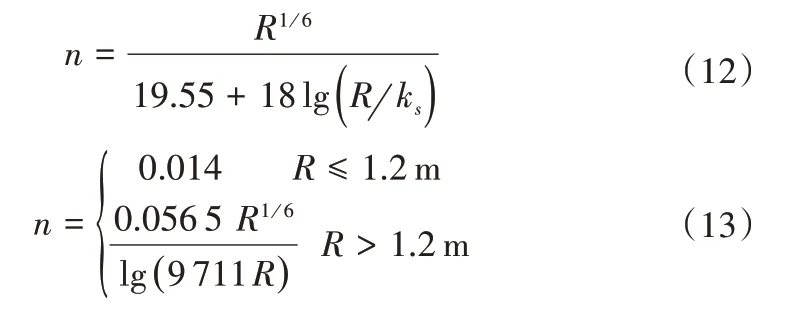
式中:ks是表征明渠表面平整度的当量粗糙高度,工程初期一般取值0.61 mm。
式(12)是目前我国工程设计中常用的明渠沿程糙率计算公式,式(13)则是美国垦务局推荐的公式。依据郭新蕾等[16]学者的研究,两者的差异事实上仅在参数常量的取值方面,这也在事实上反映了两国在模型试验和原型观测方面的差别。
郭新蕾等[16]在南水北调中线京石段应急供水工程实测数据基础上,借助最小二乘法来无偏估计式(11)中的待定参量,建立了明渠糙率的系统辨识模型,并把该模型用于南水北调工程其他渠段,获得了良好的效果。其结果分析表明,系统辨识模型能从无偏、一致与有效估计三个层面获得高精度和稳定的沿程糙率值,能有效消除原型观测方法中随机因素的干扰,故是一类具有较强竞争力的糙率计算方法。该类方法获取的是空间平均的沿程糙率值,而尚未考虑具有时变特征的糙率值,故该方法在应用广度层面仍需改进完善。
3.3 基于水动力学方程反算的糙率优化方法
如前所述,带有糙率摩阻项的水动力学方程,考虑了水流自身的非线性对流输运过程与阻力之间的耦合,故由此隐式包含的糙率值更符合物理事实。在此基础上,基于实测数据迭代反算糙率值,更具物理真实性。但水动力学方程的数值求解具有强独立性,仅能以黑箱模型的形式嵌入到优化算法中,进而通过不断对比实测值与模拟值之间的误差,来迭代获取真实的糙率值。针对长河道长时段的非恒定水流运动,于显亮等[38]在将水流运动过程概化为恒定问题的基础上,以实测水位与计算水位的误差平方和最小为目标,利用动态规划法建立了糙率反演模型。通过实际应用验证了该模型的可用性,并指出模型精度越高,水位误差越小。但该模型与真实河道非恒定流水流运动的状态有所出入,且未考虑河床冲淤会改变水位等情况,故有待更深入的研究。
水动力学方程数值求解过程中循环往复的迭代要求优化算法必须具有自身的寻优策略,而基于问题本身特征计算的下降梯度寻优的经典优化方法,比如牛顿梯度法、双重共轭梯度法等,就难以应用于该类问题,与经典优化方法相比,通过比拟生物演化策略来开展优化计算的遗传算法和人工神经网络等智能算法,就成为该类糙率计算方法的必然选择[39]。
章少辉等[40]通过耦合水动力学算法和基本遗传算法,来同时优化地表糙率值和土壤入渗参数,获得了良好的结果,但效率有待提高。陈素红等[41]和夏铭辉等[42]通过把水动力学算法融合到多亲遗传算法及BP 人工神经网络中来寻优明渠糙率值,达到了高效获取稳定糙率值的目的。另外需特别注意的是,张潮[43]早期的河网糙率计算工作具有较强系统性和代表性,其在进行河网概化后,利用实测水文资料,采用水动力学模拟结合机器学习的方式反算糙率,提出一种复杂河网糙率直接反演法,在恒定和非恒定流态下采用BP 神经网络和GA-RBF神经网络对树状河网和环状河网分别进行河网糙率的直接反演,并对不同组合下的计算结果进行相应分析,指出GA-RBF神经网络计算效率更高,但由于设置有限的隐节点以及数据覆盖度不足,导致计算精度下降,在某些点会产生较大误差。为完成反演解的获得和检验过程,张潮[43]进一步提出了BP-Bayesian 方法,将其与直接反演法相结合,构建了完整的河网糙率反演问题解决框架。总之,张潮[43]针对复杂河网糙率首次引用了3 种技术手段:BP、GA-RBF 和BP-Bayesian,并结合算例进行了计算及分析,总结出了各方法的优缺点,并探究了分别适用的工况。鉴于灌区明渠输配水和排水网络具有显著的拓扑复杂性,加之众多闸控约束条件,故进一步融合先进的多层深度人工神经网络,实现闸控约束下复杂渠系的时空变异糙率值计算,是一个很好的解决方案。
此类方法的缺点是,计算量较大。提高水动力模拟算法效率,并选取适宜水利工程这个特定物理问题的优化方法,是克服该类方法缺点的发展方向。
3.4 基于数据同化的糙率同步求解方法
数据同化方法,就是借助卡尔曼滤波等方法,融合离散时空情景下不同来源和不同分辨率的观测数据,来自动调整数值模型的模拟结果,进而不断改进完善动力学模型的精度,提高动力学过程的预测能力。该方法的前提假设是动力学过程在短期内具有物理决定论的一致性,已被应用于洪水过程的糙率实时更新和土壤水动力学参数的计算方面,取得了良好的动力学行为预测效果[44,45]。
基于数据同化的糙率同步求解方法,事实上是上述“基于水动力学方程反算的糙率优化方法”的进一步发展,即在水动力过程模拟过程中,基于水位、流量、甚至地形等几何数据信息的不断更新完善,来不断用同化技术更新糙率值,以期获得更加精确的水动力过程预测能力。在该方面,陈一帆等[46]的工作具有一定的代表性,其实现了糙率与水位流量的同步校正,将糙率和水位流量数据作为系统变量,并采用扩展的卡尔曼滤波方法,构建了结合糙率动态校正的河网水情数据同化模型,基于丰富的实测结果,对水位、糙率初始值及其演变值以及测站个数对水动力学模型校正的影响进行了分析,结果表明,靠近测站的河道糙率同化值更接近于当前真值,远离测站的河道糙率同化值接近初始值。
数据同化方法应用于糙率的实时更新计算,目前正在不断发展中。由于结合了复杂的动力学过程实时模拟,故对糙率更新计算的实时性具有一定的要求,因此该类方法目前在不断地融合GPU 并行计算技术和大数据分析技术,具有广阔的发展前景。
4 糙率计算方法发展趋势
随着海量线程同时并发的GPU 计算技术、大数据分析技术以及web技术的快速发展,通过云端实时在线计算出高精度糙率的方式必然成为下一步的趋势[47,48]。比如,郭新蕾等[16]已经基于大数据分析技术和web技术,通过融合其建立的糙率系统辨别方法,实现了明渠糙率在线实时计算率定,相对于以往的线下延时糙率计算方式,能在各地工程现场实时开展糙率计算工作,显著提高了明渠输配水评估和管理工作效率与质量。
基于由水动力学方程反算糙率的方法具有更强物理意义的前提,水动力过程实时计算方法与技术的突破,会为糙率的实时在线计算带来革命性发展。在此,尤其值得关注的是,GPU 计算技术以及由此催生的人工智能技术,已经开始与水动力学模拟技术进行深度融合,学者们通过采用人工智能模型来并行的实时更新水动力学方程时空离散式中具有显著水运动因果律的仿射坐标组合系数[49],来实现百万量级甚至更多空间离散节点下水动力过程的高效实时模拟[50],有效克服了人工智能方法没有可解释性和泛化性的缺陷,为高效获取具有空间和时间变异特征的高精度糙率值奠定了基础[51]。这类方法融合了比傅汝德数更加精细的水运动的物理流态过程,故属于典型的物理要素影响下的糙率实时计算方法。
人工智能技术,事实上是人工神经网络在节点数量及网络层级上的进一步深化发展的结果。与前述采用人工神经网络等智能优化算法融合水动力学模拟反算糙率的方式不同。在GPU 并行技术环境下,采用现代人工智能技术进行实时高效的水动力过程模拟计算,进而反算获取糙率,事实上基于的是水动力过程具有极其直观的物理机制背景。如图1 所示,若不考虑糙率,明渠等浅水流永远都仅包含稀疏波和激波这两类基础波形,随着水流演进,亦仅是这两类基础波形的叠加和扰动,其基础波形的叠加与扰动系数,即是水动力学方程时空离散式中的仿射坐标系数,这是上述[50]工作的基本理念。在此基础上,通过人工智能技术在线实时的识别真实的流态与未考虑糙率的理想流态之间的差异(图1),便能很快计算出高精度的糙率值。事实上,从水流的物理阻力视角出发,已有学者开始开展相关工作[52,53]。
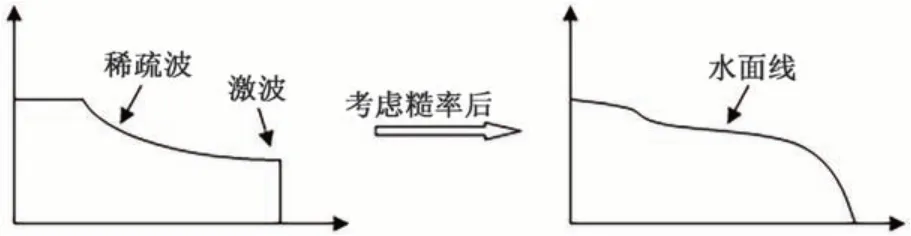
图1 存在有无水两个区域时考虑明渠糙率前后的地表浅水过程水面线Fig.1 Surface profile of surface shallow water process before and after considering roughness of open channel when there are two areas without water
与此同时,与物理要素相比,前述的影响糙率的工程要素,具有更加显著直观的实时图像特征,这为直接应用人工智能技术来实时的综合识别现场工程状况、进而实时的计算当地工程糙率值提供了基础。迄今,基于人工智能的水位和自由水面流速标志物自动识别技术已经开始应用于明渠用水管理中。如若在此基础上,再借助水动力学实时算法来校核率定相关流量过程,此时获取的具有时空变异性的当地工程糙率值会更加高效和更加精确,更能提升灌区用水过程管理的智慧化。
总之,借助GPU 并行计算技术和人工智能强悍的图形图像识别技术,来高效的获取水动力过程的基本波形信息和工程自身的几何信息,进而通过对比考虑与不考虑糙率下水动力过程的差异,来实时计算出更加符合物理真实过程的糙率值,是未来的发展趋势。
5 结 论
明渠水流运动阻力的复杂性,导致难以对其进行理论描述,由此诞生了经验性的糙率概念及表征。当前糙率计算公式和计算手段众多,但都源于法国水力学家谢才的工作,故明晰糙率定量表征的发展史,对于捋清当前各类糙率计算公式之间的关系、认清各类糙率获取方法的优缺点至关重要。为此,本文在归纳分析明渠糙率定量表征的发展及一些重要公式之间关系的基础上,把影响糙率的要素分为工程要素和物理要素两个层面,该种分类有望与现今发展迅速的人工智能技术进行深度融合。
目前,计算糙率的方法主要有原型观测方法、系统辨识方法、基于水动力学方程反算的糙率优化方法、基于数据同化的糙率同步求解方法。其中,原型观测方法是基础,因为所有衍生的方法均需基于原型观测数据。而系统辨识方法具有不受随机因素干扰的显著优点,且目前已有实时在线分析系统,在当前具有显著的实用价值。基于水动力学方程反算的糙率优化方法由于融合了明渠水流特有的物理过程,故能获取更加精确合理的糙率值,但具有效率低的缺点。而基于数据同化的糙率同步求解方法能在一定程度上弥补基于水动力方程反算糙率优化方法的缺点,提高了效率,增强了实用性。
在当前水动力学计算方法与GPU 并行及人工智能方法融合形成的海量空间节点水动力实时模拟背景下,通过借助人工智能技术强悍的图形图像识别技术,来实时的获取水动力学过程的基础波形叠加和工程复杂的几何信息,通过比较考虑与未考虑糙率的水动力过程差异,在线计算出更加符合真实物理场景的糙率值,或许是下一步的趋势。

