基于模拟退火与布谷鸟混合算法的树状灌溉管网优化设计

王永涛，刘 坚，李家春，蔡家斌，索鑫宇，李继学

（1.湖南大学汽车车身先进设计制造国家重点实验室，长沙410082；2.贵州省水利科学研究院，贵阳550002；3.贵州大学机械工程学院，贵阳550025）

0 引 言

李道西博士等[1]指出经济、合理、实用是设计灌溉管网的最终目的，管网优化方案制定应综合考虑降低能耗、节省投资和提高灌水质量。灌溉管网优化布置可视为网络图优化问题，最佳管网设计具有理论和实际双重意义。传统的灌溉管网优化主要为微分法、非线性规划法、线性规划法、动态规划法与枚举法等。当求解问题规模较大时，传统方法存在求解效率低等局限性。近年来，智能优化算法在解决规模限制问题方面，具有明显的优势。李援农教授等[2]从控制灌溉面积最大、简化灌溉管网系统、减少管网建设及运行管理成本等方面入手，基于最大控制面积和单位面积管网投资最低分别对毛管单向布置和双向布置的微灌小区建立了目标函数，设定灌水均匀度与压力为约束条件，采用遗传（Genetic Algorithm，GA）算法进行求解，得到最优化的灌溉管网布置与管径组合方式。该研究从灌区整体出发，通过压差（坡度或地形高差）与水头损失（局部水头损失、沿程水头损失）计算得出各灌水节点的相对压力值，具有方法简单且易于获得最优解的特点。马孝义等[3]对树状输配水管网进行两级优化，第一级采用单点供水的原则，构建GA 算法优化布置模型；第二级根据整数编码的原则，构建投资最低的GA 算法优化模型。胡杰华等[4]为解决灌溉管网布置和管径优化问题，建立管网投资最低的目标函数，采用结合设计者实际工程经验的Kruskal 算法求解灌溉管网最小生成树。实践表明，该方法能较好解决局部最优解的问题，高效求解出符合工程实际的树状管网布置和管径。范兴业[5]、马雪琴[6-7]等采用GA 算法开展树状灌溉管网的优化设计，具有较强的指导意义，但受遗传算子的影响，求解结果稳定性较差。朱成立等[8]采用蚁群优化（Ant Clony Optimization，ACO）算法对树状灌溉管网的管径和布置进行了优化设计，实例研究表明，ACO 算法解决了搜索方向不明确、效率低等问题，对实际工作具有借鉴意义，但易于陷入局部最优的问题。付玉娟等[9,10]认为灌溉制度、灌水方式会直接影响灌溉配水管网的流量分配模式，进而影响工程的总投资。同时通过对轮灌工作制度下灌溉管网优化设计研究，提出了将轮灌组的划分也进行优化，用基于整数编码的遗传算法进行优化，通过VB 和MATLAB 混合编程来实现。计算结果表明提出的方法效果明显，可以应用于生产。

然而，以上单一算法在解决收敛速度过快引起早熟现象或无法找到符合条件的解以及算法后期的局部搜索能力较差等问题局限性较大。牛寅[11]提出了模拟退火遗传（Simulated Annealing Genetic Algorithm，SAGA）混合算法，针对江苏省南通市港闸区花鱼地村灌溉工程项目，分别对传统经验设计方法和SAGA 混合算法进行了对比分析，结果表明优化后的灌溉管网投资降低了19.77%，但其忽略了坡度对优化结果的影响，在山丘区地势起伏，坡度影响较大场合下，还需开展大量的研究。布谷鸟优化算法模型简单、参数少及前期搜索较快的优点，但存在搜索效率低、局部搜索效率不高等问题。同时，模拟退火算法优点是局部搜索能力较强，缺点是具有较低的搜索效率。为此，马灿等[12,13]将布谷鸟（Cuckoo Search，CS）算法与模拟退火（Simulated Annealing，SA）算法结合构建（Simulated Annealing Cuckoo Search，SACS）混合算法，充分利用布谷鸟优化算法全局搜索能力把握搜索方向，模拟退火算法的局部搜索能力提高搜索效率，以期得到更好的求解质量。通过对经典测试函数和旅行商问题进行测试，结果表明，改进后的混合模拟退火的布谷鸟算法在收敛速度以及寻优精度方面有明显提升，对于函数优化问题和组合优化问题都具有一定的优势。但其仅对经典测试函数和旅行商问题进行了测试，将算法应用到工程优化领域还需要大量研究。本文的创新点是在马灿等人研究得基础上，进一步研究SACS 混合算法在树状灌溉管网优化设计等方面得应用，将SACS 混合算法应用于具体灌溉工程，为解决灌溉工程管网优化设计实际问题提供了新的思路。

1 树状灌溉管网优化模型设计

对石阡县龙塘大屯茶叶园区216 hm2现代水利试点区工程实地调查的基础上，在等高线地形图上明确水源及各灌溉节点的位置，采用紧邻规划的原则并结合实际情况初步确定灌溉管网连接图，并确定水源至各需水节点的长度、高程及供水流量等工程特征信息。

1.1 树状灌溉管网数学建模

对灌溉管网系统的优化设计问题是指在管网布置一定，满足灌水均匀度、灌溉施肥制度、轮灌制度等一系列设计准则的前提下，实现建设投资、管理成本、运行维护成本等综合成本最低的管网最优配置。灌溉管网系统涉及的参数较多，且各参数间包含复杂的非线性关系和耦合关系，因此该设计优化问题可以看做是一个以综合成本最小为优化目标，同时满足多个约束条件的复杂的非线性问题的优化。山区地形地势起伏，多采用低压灌溉管网，构建非线性规划模型，并以管网的一次性建设投资最小为优化目标[14]。为简化模型求解过程，本文采用惩罚函数将多约束优化问题转化为无约束优化问题，进一步提高模型的求解效率。

目标函数：

式中：F′为管网一次性投入，元；Di为向第i节点供水管道的管径，mm；Li为向第i节点供水的管道长度，m；N为管网需水节点数；a、B、b为管道造价系数和指数。

（1）压力约束：

式中：I(k)为从水源到管网第k个节点处所经过的管段个数；M为标准管径数；α为局部水头损失的放大系数，通常取1.1；f、m、n为管道水头损失中与管材相关的参数，见表1；E0为自由水面高程，m；Qij为从水源到第i需水节点供水管网中的第j段管道流量，m³/h；Dij为从水源到第i需水节点供水管网中的第j段管道直径，mm；Lij为从水源到第i需水节点供水管网中的第j段管道管长，mm；Ek为管网第k个节点的地面高程，m；Hkmin为满足第k个节点处流量所需要的最小水头，m。

表1 塑料管道常用的f、m、n值

（2）管径约束：

①管径应满足标准管径：

式中：DW为可选标准管径的集合。

②管径沿水流方向应满足非增条件：

式中：Dij-1为从水源到第i需水节点供水路径中的第j- 1段管道直径，mm。

（3）流速约束：

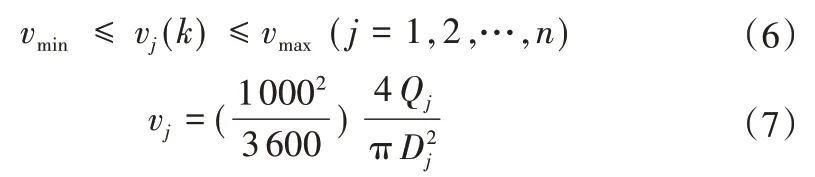
式中：vj(k)为第j段管道流速，m/s；vmax为系统允许通过的最大流速，m/s；vmin为系统允许通过的最小流速，m/s。

1.2 适应度函数的构造

采用罚函数法将有约束条件的优化问题转化为无约束的优化问题。若迭代点满足约束，则不予惩罚；否则，若不满足约束条件，惩罚较严重，惩罚值以违反约束条件的平方增大。

式中：Mp、Mv分别为压力、流速惩罚因子。

2 SACS混合算法设计

2.1 参数编码

（1）管网布置编码：按照近邻规划原则，逆时针对管段进行编号，根据节点和供水管段一一对应的关系，各个基因位上的数字代表的就是向节点供水的管段编号。

（2）管径编码：编码组合采用市场上标准商用管材的管径，鉴于管径组合均为有限的离散值，常用的二进制编码会导致冗余和非可行解等不足，本文采用整数编码的方式。不同管道的管径进行从N+ 1 到M（M为正整数）进行编码，见表2。

表2 管径编码

2.2 布谷鸟搜索操作

步骤1：种群初始化，在D维解空间中随机生成N个鸟巢，计算所有鸟巢的适应度值，并保留适应度值最优的鸟巢位置。

步骤2：设鸟巢i的位置为xi=(xi1,xi2,…xiD) ，1 ≤i≤N，计算第t次迭代的所有鸟巢的适应度值，最优的鸟巢位置保留到下一代，按式（9）进行所有鸟巢位置的更新：

式中：为鸟巢i第t次迭代的位置；N(0,1)为D维的标准正态分布；⊗为点乘；α为步长因子；step为由Lévy 分布产生的随机步长；为第t次迭代的最优鸟巢。

步骤3：设鸟巢宿主发现外来鸟蛋的概率为Pa，产生均匀分布随机数r，r∈(0,1)若r＞Pa，则对所发现的鸟巢进行随机变异，以新鸟巢替换旧鸟巢，计算所有鸟巢的适应度值，且保留适应度值最优的鸟巢位置。

步骤4：记录历史最优解，若未达到迭代终止条件，则返回步骤2。

2.3 模拟退火操作

步骤1：设初始退火温度为T0、温度冷却系数为C，建立冷却进度表Tk=C T0以及马尔可夫链的长度L。

步骤2：令T=T0，根据当前解的位置xk，按式（9）迭代产生下一代的解的位置xk+1。产生一个在(0，1)区间上均匀分布的随机数β，按式（10）计算出在给定当前解xk和温度Tk下与Metropolis接受准则相对应的转移概率P：

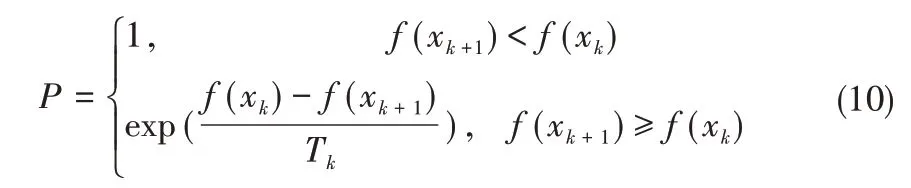
若β＜P则，接收新解，令xk=xk+1，否则xk不变。

步骤3：对步骤2 重复k次，按照冷却进度表更新当前退火温度Tk+1，进行此温度下的平衡点寻优。

步骤4：判断迭代次数是否到达马尔可夫链的长度L，若次数到达则终止算法，否则转至步骤2继续执行。

2.4 SACS混合算法流程

SACS 混合算法的基本思路是当基本布谷鸟（CS）搜索算法陷入局部最优时，随机选择部分鸟巢按式（9）进行更新，并进行模拟退火（SA）搜索，产生新的鸟巢，然后继续采用基本布谷鸟（CS）算法进行搜索。SACS 混合算法流程图见图1，主要步骤如下：

图1 SACS 混合算法流程图

步骤1：相关参数初始化。设种群数量为N，最大迭代次数为M，步长因子为α，发现概率为Pa。

步骤2：种群初始化。随机生成N个鸟巢，计算每个鸟巢的适应度值，并保留最优鸟巢的位置。

步骤3：对鸟巢位置进行Lévy 迭代。采用式（9）对鸟巢位置进行更新，计算新一代鸟巢的适应度值，并与上次鸟巢进行比较，保留更好的鸟巢。

步骤4：模拟退火过程。对除最优鸟巢外剩余的鸟巢全部进行模拟退火操作，计算所有鸟巢的适应度值，且保留适应度值最优的鸟巢。

步骤5：鸟巢宿主以概率Pa发现外来鸟蛋。产生均匀分布的随机数r，r∈(0,1)，若r＞Pa，则对所发现的鸟巢进行随机变异，以新鸟巢替换旧鸟巢，计算所有鸟巢的适应度值，且保留适应度值最优的鸟巢位置。

步骤6：记录历史最优解，若未达到迭代终止条件，则返回步骤2。

3 模型验证及分析

采用文献[14]资料数据，管道造价系数和指数为a= 0、B= 0.007 5、b= 1.438 4。设定种群规模为N= 40、最大迭代次数M= 200、步长因子α= 1、发现概率Pa= 0.1；初始温度T= 50、温度冷却系数C= 0.96、马尔可夫链长度L= 50；压力惩罚因子Mp=5、流速惩罚因子Mv=5，利用MATLAB 编程计算，得出符合实际且造价最小的方案，其中管网布置和管径优化结果如图2和图3所示。最优解的管网长度为3 600 m，投资额为1.79 万元，与文献[14]GA 算法的管网优化布置图4 相比，本文SACS 混合算法管长减少了16.27%，投资节约了2.13%；与SAGA 混合算法方法、CS 算法相比，虽管长相等，但管径优化较大，投资分别节约了3.76%、17.28%，验证了SACS混合算法的有效性，具体结果见表3。

图2 SACS混合算法的管网优化结果

图3 SACS混合算法的管网优化布置图

图4 文献[14]SA算法的管网优化布置图

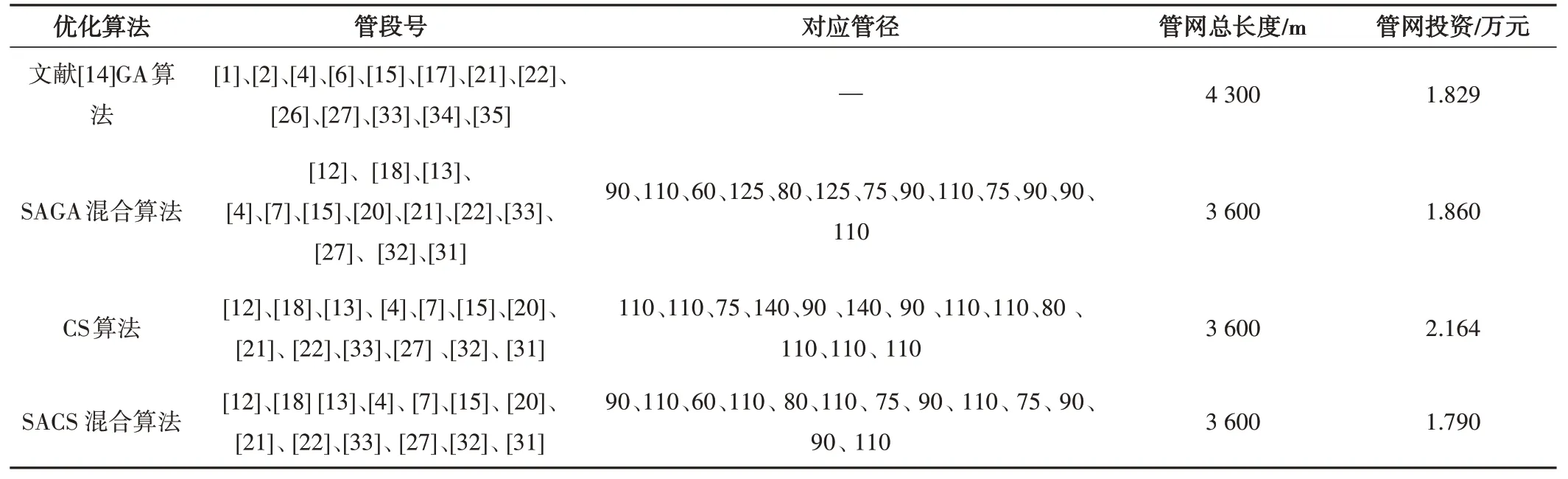
表3 优化结果对比表

4 石阡县茶叶园区灌溉管网优化设计

4.1 灌区概况

本文以贵州省石阡县龙塘大屯茶叶园区216 hm2现代水利试点区喷灌工程项目为例，开展灌溉管网优化设计。项目区平均海拔高程857 m，年平均气温16.8 ℃，年平均降水量1 105 mm，年平均日照时数1 233.2 h，全年无霜期303 d。根据《灌溉与排水工程设计标准》（GB 50288—2018）及项目区实际情况，确定灌区设计保证率为80%[15]。项目区年降水量时空分布不均，本次灌溉工程为补充性灌溉，根据《贵州省行业用水定额》（DB52T—2011）确定茶园灌溉定额为1 800 m3/hm2[16]。

4.2 管网布置

贵州省石阡县龙塘大屯茶叶园区共有12 个灌水节点，传统设计方法管网管网布置方案见图5。采用紧邻规划的原则初步确定共有42 条可能的连接方案见图6。1～12 个节点最小压力水头为10 m，管网最低流速为0.5 m/s，最高流速为3 m/s。茶叶园区灌溉管网各管段长度见表4，各节点特征见表5，不同管径的管道单价见表6。

表5 茶叶园区灌溉管网各节点特征

图6 茶叶园区灌溉管网初步连接图

表4 茶叶园区灌溉管网各管段长度

4.3 计算结果及分析

对表6灌溉管道单价回归拟合，得到管道造价系数和指数为a= 0、B= 0.004 8、b= 1.968 3。种群规模、最大迭代次数、步长因子、发现概率；初始温度、温度冷却系数、马尔可夫链长度；压力惩罚因子、流速惩罚因子等参数设定与“3模型验证与分析”节均相同。

表6 不同管径的管道单价（1.25 MPa）

采用MATLAB 编程对本文设计的SACS 混合算法进行计算[17]，得出管网布置和管径优化结果如图7 和图8 所示。不同方案下管网投资比较见表7，传统设计方法管长1 661.35 m，管网投资为14.460 506 万元；SACS 混合算法优化后的管网长度为1 649.27 m，投资为11.867 810 万元。管网总长度减少了12.08 m；管网投资节约了17.93%，灌溉工程优化效果明显。

图7 茶叶园区SACS混合算法管网布置优化结果

图8 茶叶园区SACS混合算法管网优化布置图

表7 茶叶园区不同方案下管网投资

5 结 论

本文针对树状灌溉管网投资节约的设计需求，在满足灌水均匀度、灌溉施肥制度、轮灌制度等一系列设计准则的前提下，设计了基于整数编码的SACS 混合算法，对树状管网管径及布置进行了优化，并结合文献[14]资料数据与GA 算法、SAGA 混合算法、CS 算法进行了对比分析，表明本文SACS 混合算法比GA算法管长减少了16.27%，投资节约了2.13%；比SAGA混合算法、CS算法相比，虽管长相等，但管径得到较大的优化，投资分别节约了3.76%、17.28%，验证了SACS 混合算法的有效性。

应用本文设计的SACS 混合算法，对石阡县龙塘大屯茶叶园区216 hm2现代水利试点区工程输配水管网进行优化，并与传统设计方法进行了对比，结果表明：优化后的管网长度为1 649.27 m，管网总长度减少了12.08 m。由于管径优化效果明显，故管网总投资由14.460 506 万元降低为11.867 810 万元，投资节约了17.93%，实现了灌溉管网建设投资降低的目标，为灌溉工程优化设计提供了新的思路。