数学建模竞赛对大学生创新能力的影响
孟 军,白钰莹,张战国,张誉蓉
(1.东北农业大学文理学院;2.东北农业大学公共管理与法学院,黑龙江哈尔滨 150030)
1 研究背景
我国发布的《国家中长期教育发展规划纲要(2010—2020 年)》明确指出,高校应在国家的政策鼓励下进行知识创新和技术创新,大力发挥高校在国家创新体系中的重要地位,着重培养学生的自主创新能力和解决实际问题的积极性与动手操作能力。教育部发布的《面向21 世纪教育振兴行动计划》强调要大力培养创新型人才,提高高校的人才培养质量,全面开展国家创新教育实践活动的目标,加强我国高等教育创新能力水平的提升。当前我国大学生规模在不断增长,对大学生创新能力的大力培养成为了当代素质教育的主要要求,培养创新能力是一个国家能否拥有可持续发展竞争力的一项必不可少的指标。创新能力的培养并不是一个短暂的过程,它是一个持久的、循序渐进的、在学习实践中逐渐养成的长期的过程。当前对于大学本科生的教育,更多是对大学生课本知识的教育,大学生较少去参与创新型活动,而参加数学建模竞赛这类创新实践活动便成为培养和提高大学生创新能力与创新意识的有效途径[1]。
数学建模竞赛被普遍认为是我国高等院校培养创新型人才的重要教育方式[2]。数学建模就是通过运用数学系统相关的知识方法,将一个实际问题转化成一个数学问题,应用数学的思维和语言找出其中的数学关系,并进行求解和解释的过程[3]。大学生参加数学建模竞赛的过程,也是对自身创新能力培养的过程:参赛前,各高校会由专业的教师组建竞赛培训团队对参赛生进行相关建模技术方法及数学统计软件等技能提升培训;参赛中,以3 人为一队各自分工进行题目的分析、数学模型的构建、论文的完成;参赛后,进行自我总结。在这一整个过程中,大学生的思维能力、对信息的检索能力、模型的构建和运用能力、团队之间的协作能力等都会得到一定的提升,同时对调动大学生的学习积极性、增强其创新意识和加强其科学素养培养上也起到了重要的作用[4]。
现有文献对数学建模活动的研究主要集中在3个方面。一是数学建模竞赛对大学生能力培养的研究,如曾剑熊[5]在研究第二课堂对大学生核心竞争力的影响中收集了5 年以内的大学毕业生的相关数据,实证结论为第二课堂对大学生核心竞争力有正向的显著影响;杨志斌等[6]以大连交通大学材料科学与工程学院的学生为例,通过对传统教学培养模式和以学科竞赛为依托的教学培养模式相比较,发现学科竞赛活动可以更好地去激发学生学习的积极性,有利于培养学生的综合能力,对培养学生的创新能力和实践能力具有良好的效果;张雷洪等[7]在“新工科”背景下建立了以赛促教的人才培养改革模式,促进了对学生综合素质和创新精神的培养。二是依托数学建模的课程建设和教学改革,如王晓岗等[8]以上海大学生化学实验竞赛为例,结合了学生具体的参赛过程,从各个高校参与学科竞赛的结果发现存在的实验教学问题、举办竞赛以改善竞赛实验室的条件、竞赛期间实验教学培训研讨及后续学习交流这4 个方面,阐述了学科竞赛对推动上海地区各高校实验教学改革和高校教师教学质量的提高具有明显的成效;李春阳等[9]提出了基于学科竞赛的工程训练“五位一体”的精准教学模式,在这种教学模式下可以发挥学科竞赛对学生创新能力培养的最大作用,对新形势下工程教育改革具有一定借鉴意义。三是数学建模竞赛组织管理及提高竞赛质量的研究,如沈秀等[10]以常州大学为例,对该校学科竞赛的开展进行总结和分析,认为应该加强对学科竞赛的改革和实践,从而推动学科竞赛活动管理体系的构建与完善;郑立利[11]针对学科竞赛管理上出现的问题,提出树立学科竞赛管理质量意识、追求高效率精细化管理、加强竞赛培训、开展政策奖励四点措施。
当前大多关于数学建模对大学生创新能力影响的文献,主要是通过定性研究,根据来自相关领域的经验总结进行理论的分析和经验的论述,有的学者从数学建模竞赛自身的特点出发,有的学者从数学建模竞赛赛题进行分析研究,论述数学建模竞赛对大学生创新能力的影响作用,这样的研究稍显理论高度不足、体系完善程度欠缺[12]。同时,当前对于数学建模竞赛活动开展的效果究竟如何,并没有较为科学、系统化的评价。因此,本研究主要从大学生创新能力培养的角度,运用定量分析方法,通过对农业类院校、工科类院校和综合类院校这3种不同类型的大学中参加过和未参加过数学建模竞赛的大学生发放调查问卷,并通过模糊综合评价法和层次分析法对这两组大学生进行创新能力评价,研究数学建模竞赛对大学生创新能力的影响。
2 大学生创新能力评价指标体系的构建
2.1 评价指标确定的依据和指标体系
根据对大学生创新能力评价相关国内外文献的整理和归纳,在教育评价理论和建构主义学习理论基础上,参考邓成超[13]提出的大学生创新素质的量质化评价指标体系和曹颖颐[14]的研究,同时还参考了大量优秀文献中所构建的大学生创新能力评价指标体系,运用德尔斐法,结合了专家的意见,遵循客观性、科学性和严谨性原则,确定了包含创新学习能力、创新知识基础、创新思维能力、创新实践操作能力这四大方面作为创新能力的一级指标。创新能力是由多种能力要素构成的,而这是学者们从不同角度、层面上分析的结果,并且对于不同的能力要素指标要进行进一步分解,从而形成一套评价指标体系,为此,本研究整理出了与大学生创新能力评价一级指标要素相关的指标,经过讨论、修改和完善,确定了大学生创新能力评价的二级指标及相关要素标准。将已整理和确定的评价标准以问卷的形式发放给25 位相关领域的专家学者,在征求他们意见后,最终构建了由4 个一级指标和13 个二级指标构成的大学生创新能力综合评价指标体系(见表1)。其中,结合数学建模竞赛活动的特点,将大学生创新能力分解为创新学习能力、创新知识基础、创新思维能力、创新实践操作能力这4 个方面。创新学习能力是评价学生创新能力的前提,它是学生在现有知识素养的基础上对新知识的探索、实践和思考,从而获得新的想法、新的观点和新的方法等的学习能力。创新学习基础是学生创新能力培养的基础,只有具备一定的知识素养才能更有效地培养创新能力。创新思维能力是学生创新能力培养的核心。创新实践操作能力是评价学生创新能力的实践表现。

表1 大学生创新能力评价指标体系及要素标准
2.2 评价指标体系的检验
2.2.1 信度检验
信度检验是指问卷的可靠性检验。对于调查问卷中的李克特量表题项,常常用到的检验方法是克朗巴哈系数(Cronbach'sα,以下简称“α系数”)检验量表的内部一致性程度。若α系数是低于0.6,说明量表的内部一致信度不足,信度效果不好;若是α系数是在0.6~0.8 之间,说明量表具有一定信度,信度效果较好;若是α系数大于0.8,说明量表的信度效果非常好。由表2 可知,本研究量表的α系数大于0.8,表明问卷信度较高,可信度很好。

表2 评价指标信度检验结果
2.2.2 效度检验
通过探索性因子检验(KMO 检验和Bartlett 球形度检验)来说明调查问卷的有效程度,从而在有效的基础上更好地分析问卷的数据结果。若KMO 的值越接近于1,说明因子间的相关性越强,更适合做因子分析,且规定KMO 的值至少要比0.6 大。由表3 可知,KMO 值为0.837,是大于0.8 的,说明本研究测量量表的各变量间相关性较强。Bartlett 球形检验的P值为0.000<0.01,检验结果显著。

表3 评价指标效度检验结果
2.2.3 差异分析
为了解不同变量在大学生创新能力以及大学生创新能力各维度上是否存在差异,对调研数据采用独立样本T 检验运用独立样本T 检验分析参加过数学建模竞赛和未参加过数学建模竞赛的大学生在大学生创新能力及大学生创新能力各维度上是否存在显著的差异,并分析不同性别的大学生创新能力是否存在显著差异;采用单因素方差分析(ANOVA)方法分析获奖级别、年级、专业在大学生创新能力及大学生创新能力各维度上是否存在显著差异。
(1)参赛经历维度下大学生创新能力的差异性。从表4 可知,是否参加过数学建模竞赛在大学生创新能力以及大学生创新能力各维度上是存在显著差异的,参加过竞赛的大学生的创新能力要高于未参加过竞赛的大学生,尤其在创新实践操作能力这一方面,参加过竞赛的大学生要高出未参加过的大学生很多。
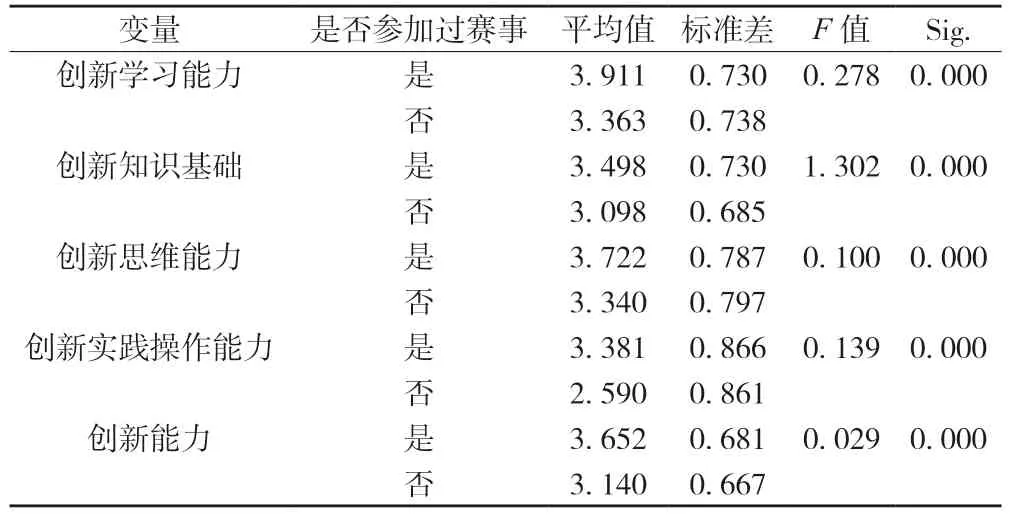
表4 参赛经历对大学生创新能力的差异性分析
(2)参赛者性别维度下大学生创新能力的差异性。从表5 数据可知,不同性别的大学生的创新能力以及在大学生创新能力各维度上都不存在显著的差异。

表5 参赛者性别对大学生创新能力的差异性分析
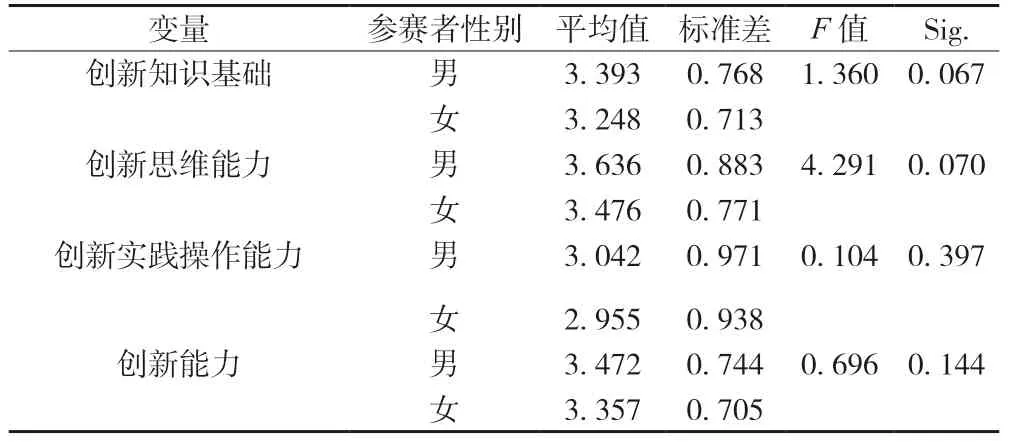
表5 (续)
(3)参赛获奖级别维度下大学生创新能力的差异性。本次调查的大学生参赛获奖级别共分为4 种情况,分别是在数学建模竞赛中没有获得过奖项、获得过校级奖项、获得过省级奖项和获得过国家级奖项。从表6 可以看出,获奖级别不同的大学生在大学生创新能力以及大学生创新能力各维度上均存在显著差异。

表6 参赛获奖级别对大学生创新能力的差异性分析
(4)参赛者所在年级维度下大学生创新能力的差异性。本次调查的大学生所在年级共分为4 种情况,分别是一年级、二年级、三年级和四年级。从表7 可以看出,除了创新实践操作能力这一指标以外,不同年级的大学生在大学生创新能力以及大学生创新学习能力、创新知识基础、创新思维能力这3 个维度上均不存在显著差异。

表7 参赛者所在年级对大学生创新能力的差异性分析
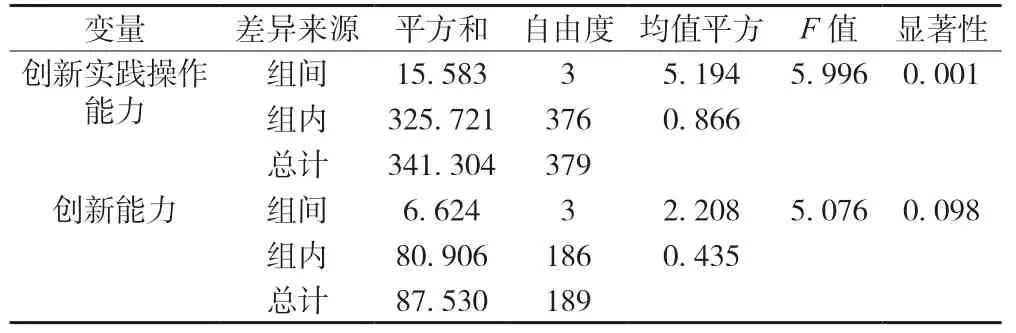
表7 (续)
(5)参赛者专业维度下大学生创新能力的差异性。本次调查的大学生所在专业共分为4 种情况,分别是文科、理科、工科和艺术。从表8 可以看出,不同专业的大学生在大学生创新能力以及大学生创新能力的各个维度上均不存在显著差异。
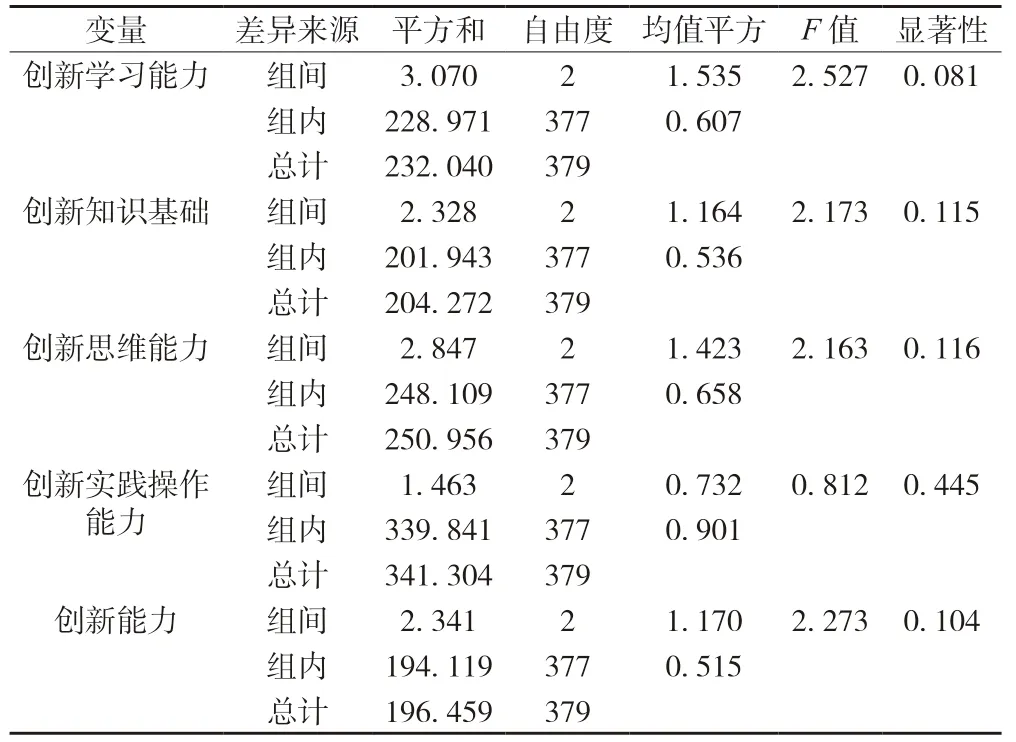
表8 参赛者专业对大学生创新能力的差异性分析
综上所述,是否参加数学建模竞赛和参加数学建模竞赛的获奖级别不同在大学生创新能力以及大学生创新能力的各个维度上均存在显著差,而性别不同、所在年级不同和所在专业不同的大学生在大学生创新能力以及大学生创新能力的各个维度上均不存在显著差异。
2.3 指标权重的计算
本研究选取了某大学25 名常年从事数学建模工作的专家、教授对各指标的重要程度进行评价,并运用层次分析法得到各指标的权重值,结果如表9所示。一级指标中,创新实践操作能力所占比重最大(0.298),其中创新实践能力占比较大(0.674);其次是创新学习能力(0.287),其中发现问题能力占比较大(0.413);创新思维能力(0.286)排名第三,其中逻辑思维能力(0.287)和创新想象能力(0.273)占比较大;创新知识基础所占比重(0.129)排名第四,其中专业知识水平占比较大(0.468)。由此可得,在数学建模竞赛对大学生创新能力影响的评价中,创新实践操作能力指标最重要,尤其是创新实践能力;其次是创新学习能力指标和创新思维能力指标,其中发现问题能力相较于逻辑思维能力和创新想象能力重要;最后是创新知识基础指标,专业知识水平相较于基础知识水平和交叉知识水平重要。

表9 大学生创新能力评价指标体系及权重
3 实证研究
设立参加过数学建模竞赛和未参加过数学建模竞赛大学生两个对照组,运用模糊综合评价模型对两组学生的创新能力情况进行评价,并得出评价结果。
3.1 数据收集
根据上述大学生创新能力评价指标体系设计了“大学生创新能力评价问卷”,通过问卷星发放给农业类、工科类和综合类院校参加过和未参加过数学建模竞赛的大学生,其中涉及到一年级到四年级各个专业的大学生,回收有效问卷980 份。问卷数据中,参加过数学建模竞赛的有420 人。根据问卷统计数据计算评价结果。
3.2 数据分析
3.2.1 确定评价对象的因素集
评价对象因素集U是由二级指标的各个指标构成的集合。
3.2.2 确定评价等级
将评价等级分为5 个级别,可以表示为V={ 优,良,中,差,很差} 。
3.2.3 评价结果量化处理
评价等级量化结果如表10 所示。

表10 大学生创新能力评价等级划分
3.2.4 模糊综合评价法计算评价分数
(1)参加过数学建模竞赛的大学生创新能力综合评价。根据统计的评价结果,对每项指标进行等级评定实现归一化处理(见表11)。
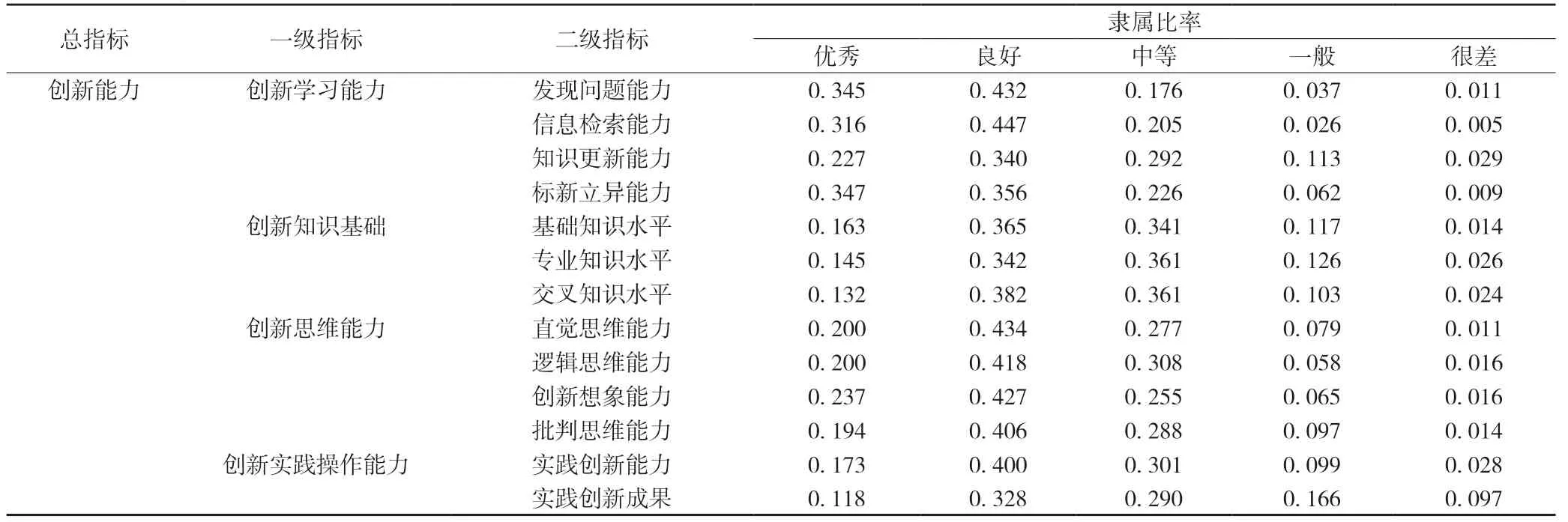
表11 参与数学建模竞赛的大学生创新能力平均评价等级
根据表11 中确定模糊关系矩阵RA:

由表9 可知创新学习能力的权重AA=(0.413,0.196,0.287,0.102),计算创新学习能力模糊综合评价向量BA,即BA=AA×RA=(0.345,0.413,0.287,0.113,0.029)。同理可得:创新知识基础模糊综合评价向量BB=(0.163,0.342,0.361,0.127,0.026);创新思维能力模糊综合评价向量BC=(0.237,0.287,0.287,0.097,0.016);创新实践操作能力模糊综合评价向量BD=(0.173,0.400,0.301,0.167,0.097);创新能力模糊综合评价向量B1=(0.287,0.298,0.298,0.167,0.097)。此时,创新能力模糊综合评价向量B1就是参加过数学建模竞赛大学生的综合评价结果。依据最大隶属原则,数值最大所对应的等级即为创新能力情况评价等级,因此,参加过数学建模竞赛的大学生创新能力处于良好和中等之间的水平。
计算出参加过数学建模竞赛的综合评价分数P1,即:

同理可得:创新学习能力得分PA=82.85 分;创新知识基础得分PB=79.81 分;创新思维能力得分PC=75.66 分;创新实践操作能力得分PD=78.37 分。从评价结果可知,参加过数学建模竞赛的大学生的创新学习能力较强,创新知识基础较为扎实,创新思维能力和创新实践操作能力相对较好,但仍需要进一步的提高,总体说明参加了数学建模竞赛的大学生的创新能力处于良好与中等之间水平。
(2)参与数学建模竞赛获得各类级别奖项的大学生创新能力模糊评价。方法同上,根据评价等级数据计算出参加数学建模竞赛中获得国家级奖项的大学生的创新能力模糊综合评价向量B2=(0.287,0.298,0.262,0.126,0.024),评价分数P2=81.70 分;获得省级奖项大学生的创新能力模糊综合评价向量B3=(0.298,0.298,0.287,0.140,0.040),评价分数P3=81.34 分。此时,创新能力模糊综合评价向量B2和B3就是参加数学建模竞赛中获得国家级和省级奖大学生的综合评价结果,依据最大隶属原则,数值最大所对应的等级即为创新能力情况评价等级。因此,参加了数学建模竞赛并获得国家级和省级奖大学生的创新能力均处于良好偏上的水平。
(3)未参加过数学建模竞赛的大学生创新能力综合评价。根据统计的评价结果,对每项指标进行等级评定实现归一化处理,如表12 所示。
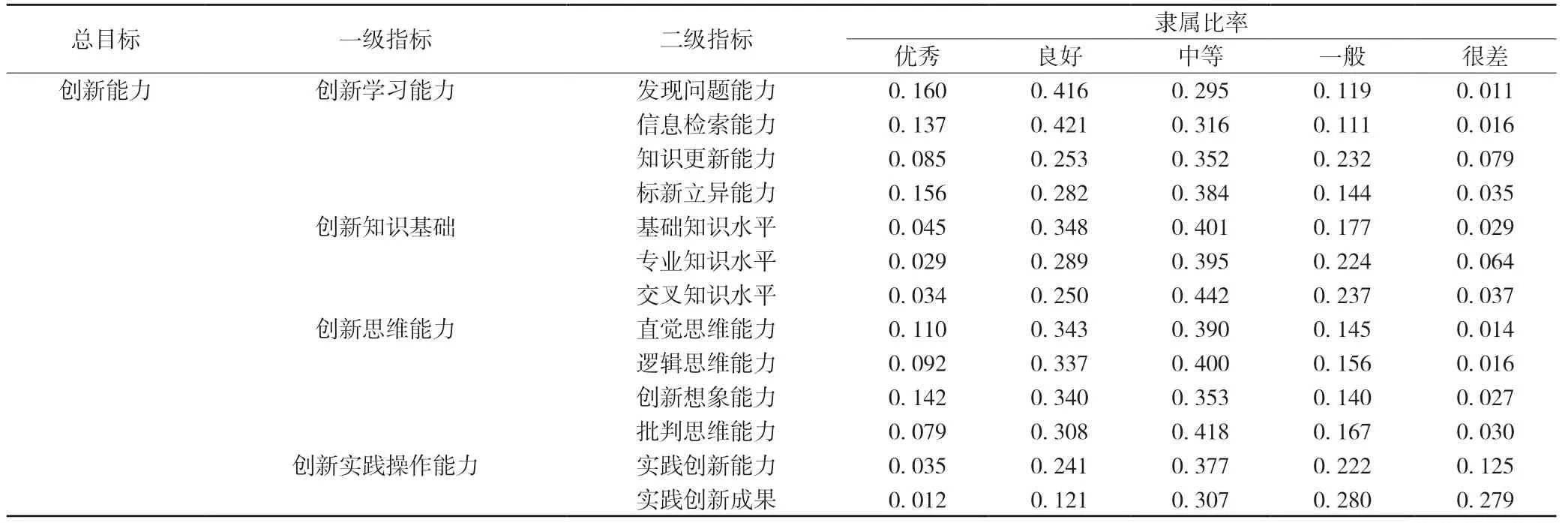
表12 未参与数学建模竞赛的大学生创新能力平均评价等级
根据表12,计算创新学习能力模糊综合评价向量BA,即BA=(0.160,0.413,0.287,0.232,0.079)。同理可得:创新知识基础模糊综合评价向量BB=(0.045,0.296,0.395,0.236,0.046);创新思维能力模糊综合评价向量BC=(0.142,0.287,0.287,0.167,0.030);创新实践操作能力模糊综合评价向量BD=(0.035,0.241,0.377,0.280,0.279);创新能力模糊综合评价向量B4=(0.160,0.287,0.298,0.280,0.279)。此时,创新能力模糊综合评价向量B4就是未参加数学建模竞赛大学生创新能力的综合评价结果,依据最大隶属原则,数值最大所对应的等级即为创新能力情况评价等级。因此,没有参加数学建模竞赛的大学生创新能力处于中等水平。
计算出未参加过数学建模竞赛的评价分数P4为:

同理可得:创新学习能力得分PA=77.93 分;创新知识基础得分PB=75.23 分;创新思维能力得分PC=71.87 分;创新实践操作能力得分PD=70.65 分。从评价结果可知,没有参加数学建模竞赛的大学生的创新学习能力评级得分相对较高,创新学习能力处于中等偏上水平,而创新知识基础、创新思维能力和创新实践操作能力还需要进一步培养与提升,总体说明没有参加数学建模竞赛的大学生的创新能力水平处于中等偏下水平,还有待提高。
3.3 评价结果分析
3.3.1 各类指标评价结果分析
为了更好地说明数学建模竞赛对大学生创新能力的具体影响,对参加数学建模竞赛和未参加的大学生的创新学习能力、创新知识基础、创新思维能力和创新实践操作能力进行了对比分析,如表13所示。可以看出,参加数学建模竞赛的大学生在创新学习能力、创新知识基础、创新思维能力和创新实践操作能力上的评价得分都要高于没有参加数学建模竞赛的大学生。具体来看,创新实践操作能力是参赛大学生和未参赛大学生创新能力中变化百分比最高的,说明数学建模竞赛注重学生将理论知识运用于实践的能力,锻炼学生更好地去运用知识解决实际问题,从而提高学生的创新性;其次是创新学习能力和创新知识基础,这两个指标在参赛大学生和未参赛大学生中的变化百分比分别为6.31%和6.09%,说明大学生通过数学建模培训能够较为熟练地运用数学软件并通过数学软件构建所需的数学模型,而且在竞赛中通过小组成员的互相讨论和意见的发表,不断拓展思维,使大学生能够更加主动地去发现问题和解决问题,也提高了大学生的学习意识和创新意识,从而更好地培养了大学生的创新学习能力和创新知识基础;对于创新思维能力,参赛和未参赛学生的变化百分比为5.27%,变化幅度相对较小,说明对于创新思维能力的培养是一个循序渐进的过程,需要学生不断地去学习和锻炼,并且要更加积极地去参加有关创新活动,才更利于自己创新思维能力的培养和提高,从而可以说明数学建模竞赛对学生创新思维能力的培养有一定的促进作用。所以,总体上来说,数学建模竞赛对大学生的创新实践操作能力影响最为显著,其次是创新学习能力、创新知识基础和创新思维能力。
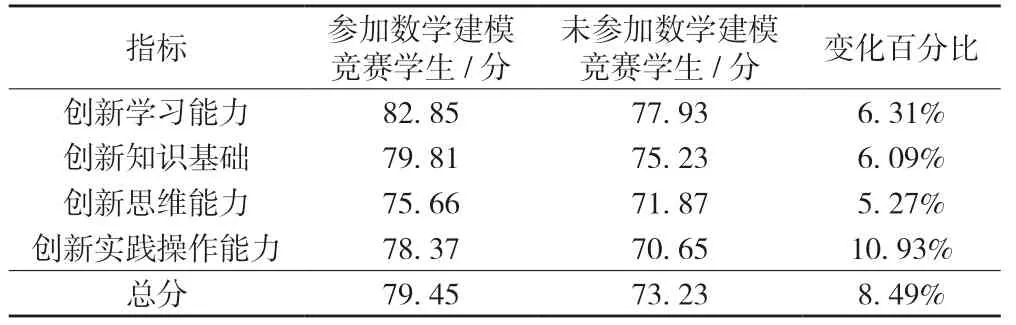
表13 数学建模竞赛对大学生创新能力影响评价
3.3.2 总指标评价结果分析
通过对数学建模竞赛对大学生创新能力影响的具体分析,进一步对参赛和未参赛大学生在创新能力上的评价分数进行总体上的对比分析,如表14 所示,可以得出:参赛获国家级奖学生的评价分数>参赛获省级奖学生的评价分数>参赛学生的总体评价分数>未参赛学生的总体评价分数。

表14 数学建模竞赛经历对大学生创新能力影响评价
综上所述,通过评价结果的对比,说明参加过数学建模竞赛的大学生的创新能力相对于没有参加过数学建模竞赛的大学生较强,而且其创新能力水平大都处于良好水平以上。除此之外,还可以从评价结果看出,参加数学建模竞赛获得奖项的大学生的创新能力水平要明显高于未参加数学建模竞赛大学生的创新能力水平,特别是获得国家级奖的大学生的创新能力。所以可以得出,数学建模活动对于大学生的创新能力是有显著影响的,有助于大学生创新能力的培养。但其中也反映了一个问题:从评价分数看,参加过数学建模竞赛的大学生的总体创新能力水平是介于中等与良好之间,未参加过数学建模竞赛的大学生的总体创新能力水平是介于一般与中等之间,说明大学生总体的创新能力水平状况较为一般,还有待提高。
4 结论
本研究从数学建模竞赛对在校大学生创新能力影响的评价分析的结果显示,参加过数学建模竞赛的学生创新能力得分是79.45 分,而未参加过数学建模竞赛的学生创新能力得分是73.23 分,说明数学建模竞赛参与对在校大学生创新能力的培养是有显著的促进作用的;对在数学建模竞赛中获得过奖项的学生的创新能力评分结果显示,获得过国家级奖项的学生的创新能力得分是81.70 分,获得过省级奖项的学生的创新能力得分是81.34 分,说明在数学建模竞赛中获奖级别的不同在大学生的创新能力上是具有较为显著的差异,对大学生创新能力的培养有促进作用;而通过独立样本T 检验和单因素方差分析得出不同性别、年级、专业在大学生的创新能力上均不存在显著差异。从数学建模竞赛对大学生创新能力各维度影响的变化百分比数据上可以看出,通过参与数学建模竞赛,学生的创新实践操作能力提升是最为明显的,其次是学生的创新学习能力和创新知识基础,最后变化幅度最小的是学生的创新思维能力。从总体来看,目前大学生总体的创新能力水平还有待提高,应加强对数学建模竞赛机制的完善,提高数学建模竞赛对大学生创新能力提高的影响效力,促进我国创新型人才的培养。

