转子式压缩机的可靠性建模与分配

迟 莹，李红旗，朱红伟

（1.北京工业大学 环境与能源工程学院，北京 100124；2.珠海格力电器股份有限公司，广东珠海 519070）

0 引言

可靠性模型是从识别系统的故障规律、反映系统的主要故障特征的角度对系统及其组件进行建模，并用于预测或估计产品的可靠性。可靠性建模是进行可靠性设计与分析的基础，也是开展系统维修性和保障性设计分析的基础。

目前针对转子式压缩机数学模型的研究主要集中在性能分析方面，如系统控制模型、几何模型、热力学模型、动力学模型、泄漏模型、传热与流动模型等[1-6]。但在可靠性设计方面开展的研究较少，尚处于起步阶段。针对压缩机结构优化，主要涉及的方法包括：FMEA/FEM综合可靠性分析法[7]、结合有限元技术和概率设计方法[8]、模糊可靠性设计[9]、考虑材料离散性[10-14]等。

转子式压缩机的全封闭结构决定了其不可维修性的特点，因此在传统的设计过程中，为保证规定寿命和无故障运行时间，通常选取高的安全系数，这造成严重的零部件过度设计问题。在当前中国巨大的制造规模下，开展转子式压缩机的可靠性研究与可靠性设计具有重要的意义。

本文基于可靠性建模相关理论知识，对某型号转子式压缩机初步构建可靠性模型，在此基础上，进行可靠性指标分配。

1 转子式压缩机可靠性建模

1.1 系统划分与定义

1.1.1 系统定义

根据可靠性工作的特点和转子式压缩机的结构特征，将转子式压缩机划分为7个系统：基础部件、电机、泵体、润滑系统、储液器、曲轴部件以及其他附件。各个系统的具体含义和组成如下。

（1）基础部件：其他零部件赖以连接、固定和运动的基础。包括机壳组件、上盖组件、下盖等。

（2）电机：将电能转换为动能，驱动曲轴进行转动。包括定子、转子、机座等。

（3）泵体：实现气体压缩。包括气缸、滚动转子、滑片、滑片弹簧、阀片等。

（4）润滑系统：向压缩机各摩擦副供油，起减少摩擦、带走摩擦热和磨屑、密封作用。包括润滑油、冷冻油、导油片等。

（5）储液器：起气液分离、储存制冷剂液体及缓冲吸气压力脉动的作用。包括进气管、滤网组件、出气管等。

（6）曲轴部件：曲轴带动转子沿着气缸内壁转动，传递运动和动力，是转子式压缩机实现旋转运动的执行件之一。包括曲轴、曲轴支承部件等。

（7）其他附件：除上述组成以外的其他附属装置。

在各系统功能的基础上，对其进行功能层次划分如图1所示。

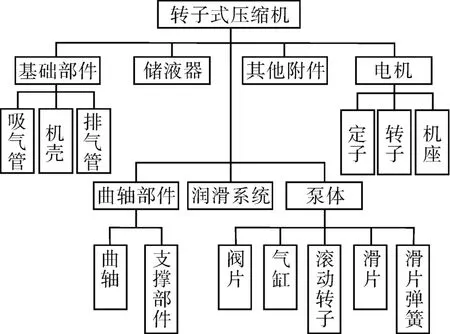
图1 转子式压缩机功能层次Fig.1 Function hierarchy diagram of rotor compressor

1.1.2 功能框图

通过对转子压缩机的系统划分与定义，可以了解各系统的功能、各系统之间的相互关系以及系统内部的接口，分析得到转子式压缩机的功能框如图2所示。

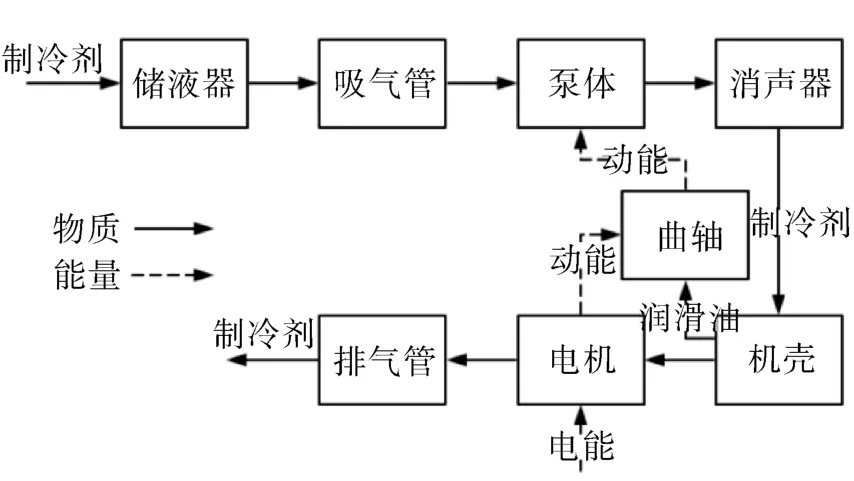
图2 转子式压缩机功能框图Fig.2 Functional block diagram of rotor compressor

基本可靠性的故障判据为：寿命期内与转子式压缩机设计、制造有关的零部件故障（如滑片损坏、弹簧断裂等），都需要必要的保障性工作，影响压缩机的基本可靠性，均计为关联故障。

任务可靠性的故障判据为：凡由于转子式压缩机设计、制造缺陷造成的不能完成吸、排气以及压缩或可能造成压缩机漏气、漏电等运行故障，均计为影响任务与安全的关联故障。

1.2 可靠性建模中采用的假设条件

（1）所有组成部件只有故障与正常两种状态，不存在第3种状态。如转子磨损，虽然影响性能，但可以正常工作，记为正常状态。

（2）系统所有输入在规定范围之内，如不考虑电压不稳定等造成系统故障的情况。

（3）所有部件的寿命均服从于指数分布，部件内的所有故障都导致部件功能故障。

1.3 可靠性框图

1.3.1 转子式压缩机可靠性框图

直接导致转子式压缩机非正常停机的故障可能发生在电机、泵体系统、润滑系统、曲轴部件系统、储液器系统、其他部件系统。上述各系统对保证压缩机正常稳定运行缺一不可，图3示出各系统串联模型。

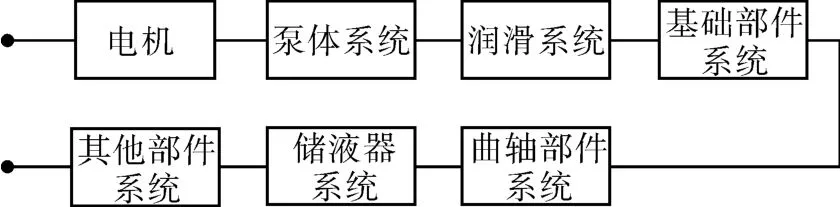
图3 转子式压缩机可靠性框图Fig.3 Reliability block diagram of rotor compressor

由此可按照一定的结构层次建立7个子系统的可靠性模型，其中，泵体系统是转子式压缩机中重要组成部分，故以之为例，建立可靠性框图以及进行可靠度分配分析，其余系统可参照进行，本文不再赘述。

1.3.2 泵体系统可靠性框图

泵体系统严重故障包括弹簧失效、滑片卡死、泵体异物、滑片与滑片槽的配合间隙过小、滑片与滑片槽刮伤、阀片故障等。由于这些严重故障都有可能造成压缩机非正常停机，因此各组件之间为串联关系，如图4所示。

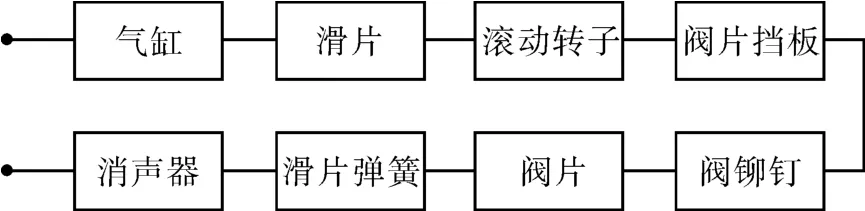
图4 泵体系统可靠性框图Fig.4 Reliability block diagram of pump body system

2 转子式压缩机可靠性分配

可靠性分配是把系统规定的可靠性指标（故障率或可靠度）按一定的数学方法合理地分配给各分系统或元件。

2.1 可靠性分配原则与方法

根据转子式压缩机的结构与特点，按照下列原则进行可靠性指标分配：

（1）对于复杂度高的系统分配较低的可靠性指标。因为系统越复杂，组成单元越多，达到高可靠性就越困难且费用高。

（2）对于重要度较高的产品分配较高的可靠性指标。因为重要度高的产品的故障率会影响系统的安全运行。

（3）当把可靠度作为分配参数时，对于需要长时间运行的产品，应分配较低的可靠性指标。这是因为可靠度是随着工作时间的增加而降低的。

2.1.1 重要度和复杂度分配法

重要度和复杂度都是定量指标，分别用ωi（j）和Ci表示。重要度表示各系统的故障对产品故障的影响；复杂度表示某个系统中基本构成部件数所占的百分比。

首先统计各系统的组成单元部件数以及工作时间，然后分析分配系统的可靠性框图模型，根据重要度和复杂度的定义，计算各系统的ωi（j）、Ci。

2.1.2 评分可靠性分配法

2.2 当量运行时间

在进行可靠性分配时，需要确定压缩机的工作时间。当前大量的转子式压缩机为变频压缩机，且未来的占比将不断增加。而频率变化对压缩机系统可靠性的影响可分为两种：一种是与转速无关的系统，如基础部件、储液器等，其运行时间就是压缩机开机时间；另一种是与转速相关的部件，如泵体系统、曲轴系统，其可靠性除开机时间外还受频率变化的影响。为此引入当量运行时间的概念，将不同频率下的运行时间折算到额定频率运行时间，综合考虑开机时间和转速的影响。

压缩机运行频率主要取决于环境温度（假定室内温度设定不变），包括地域差异和环境温度变化两个因素。对于制冷运行，根据不同地区的逐时环境温度变化设定开机温度以确定运行时间。对于制热运行，除考虑开机温度外，还需考虑北方地域集中供暖的影响（集中供暖期间无开机）。

当量运行时间分析如图5所示，通过DeST-H软件获取某城市一年的逐时环境温度、建筑单位面积冷（热）负荷，根据环境温度可得到额定频率下房间空调器制冷（热）量，定义频率系数=房间负荷/额定频率制冷（热）量，根据频率系数可得到当量运行时间=时间步长×频率系数，累加所有时刻的当量运行时间即可得到该城市累计开机时间内当量运行时间总和。

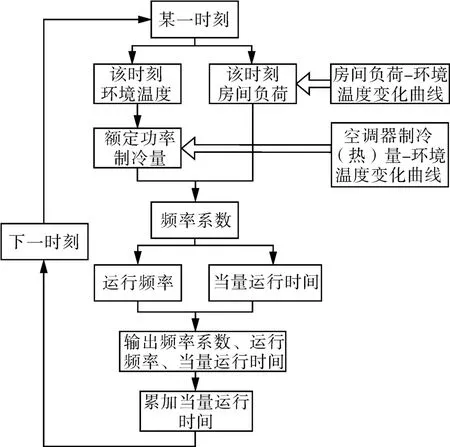
图5 当量运行时间分析流程Fig.5 Flow chart of equivalent running time analysis

可靠性分配应该可以满足最不利情况下的可靠性要求。为此选取典型北方城市北京和哈尔滨（冬季集中供暖）、典型南方城市广州和海口、中部城市上海和武汉进行计算，结果见表1。

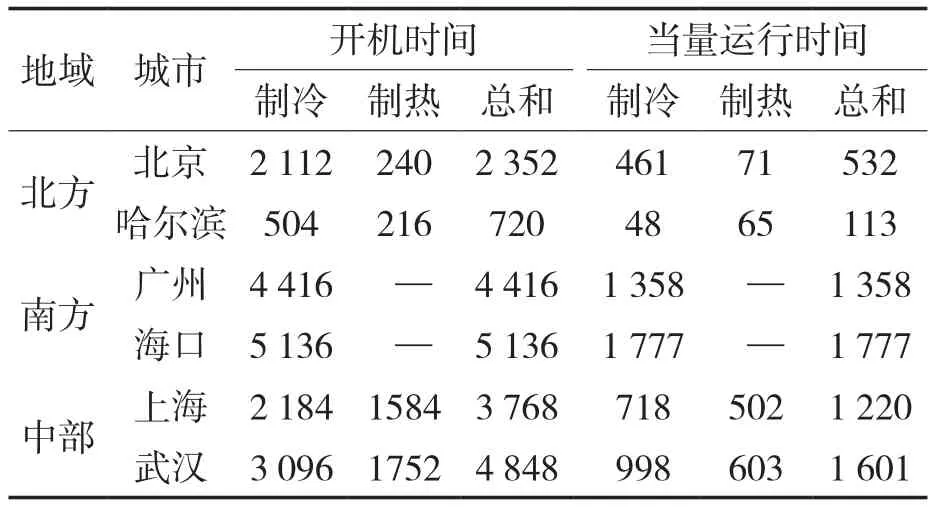
表1 各城市当量运行时间计算Tab.1 Calculation table of equivalent running time in each city h

从表1可以看出，6个城市中海口为最不利情况，其当量运行时间最大，为1 777 h/a。以此作为可靠性分配时压缩机的运行时间，按照10年寿命计算，取整为18 000 h。

2.3 转子式压缩机系统可靠性分配

期望转子式压缩机系统10年间运行18 000 h的可靠度，对该可靠度在各系统中进行分配。

按照对转子式压缩机系统的划分，将压缩机零部件进行归类并确定每个组成系统的工作时间及重要度。工作时间按照当量运行时间概念选取18 000 h，由压缩机可靠性框图（图3）可知，转子式压缩机的7个子系统之间为串联关系，故各系统重要度都为1.0（见表2）。

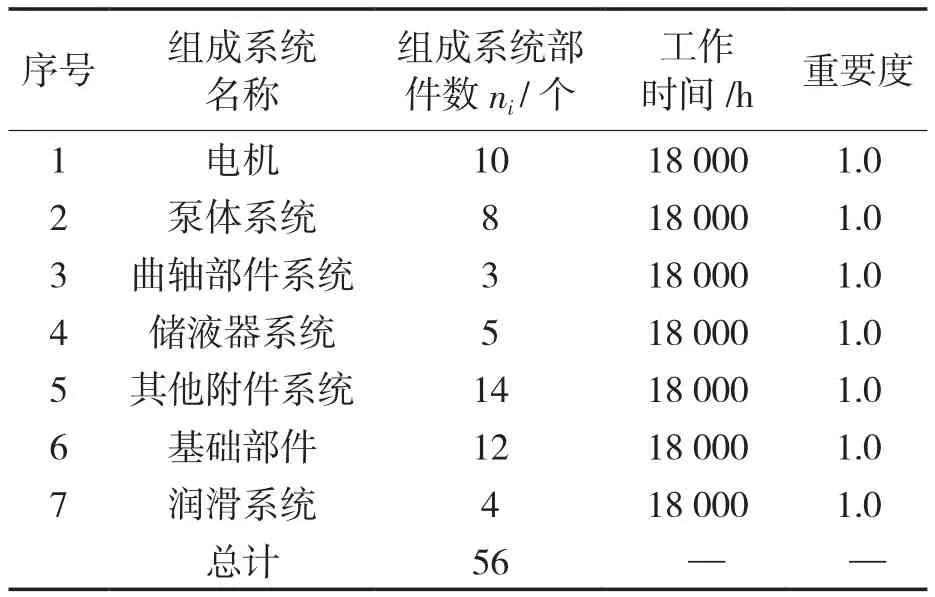
表2 转子式压缩机相关数据Tab.2 Relevant data of rotor compressor

采用重要度和复杂度分配法对转子式压缩机的可靠度进行分配，结果见表3。从可靠度分配结果来看满足规定。为使压缩机安全稳定地运行，曲轴部件系统分配了高的可靠度0.999 5，此外润滑系统和电机也分配了较高的可靠度。

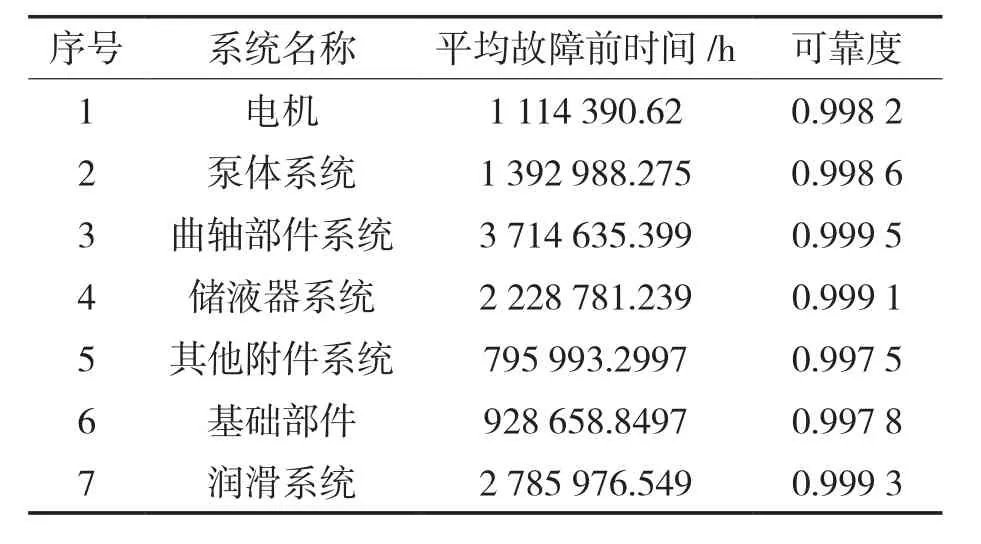
表3 压缩机各系统可靠度分配Tab.3 Reliability distribution table of compressor systems

2.4 泵体系统的可靠性分配

2.4.1 评分可靠性分配

由于泵体系统结构相对简单，故采用评分法进行泵体系统的可靠性分配。考虑到转子式压缩机主要零件的失效形式及影响原因，选用运行环境重要度、复杂度、磨损情况作为评价可靠性的影响因素，具体情况见表4。采用评分法时，首先按照各因素对可靠性的要求，划分为4个等级，等级标号越高对可靠性要求越低，分配的不可靠度或故障率越高。参考其他相关标准，压缩机可靠性影响因素等级划分标准见表5。

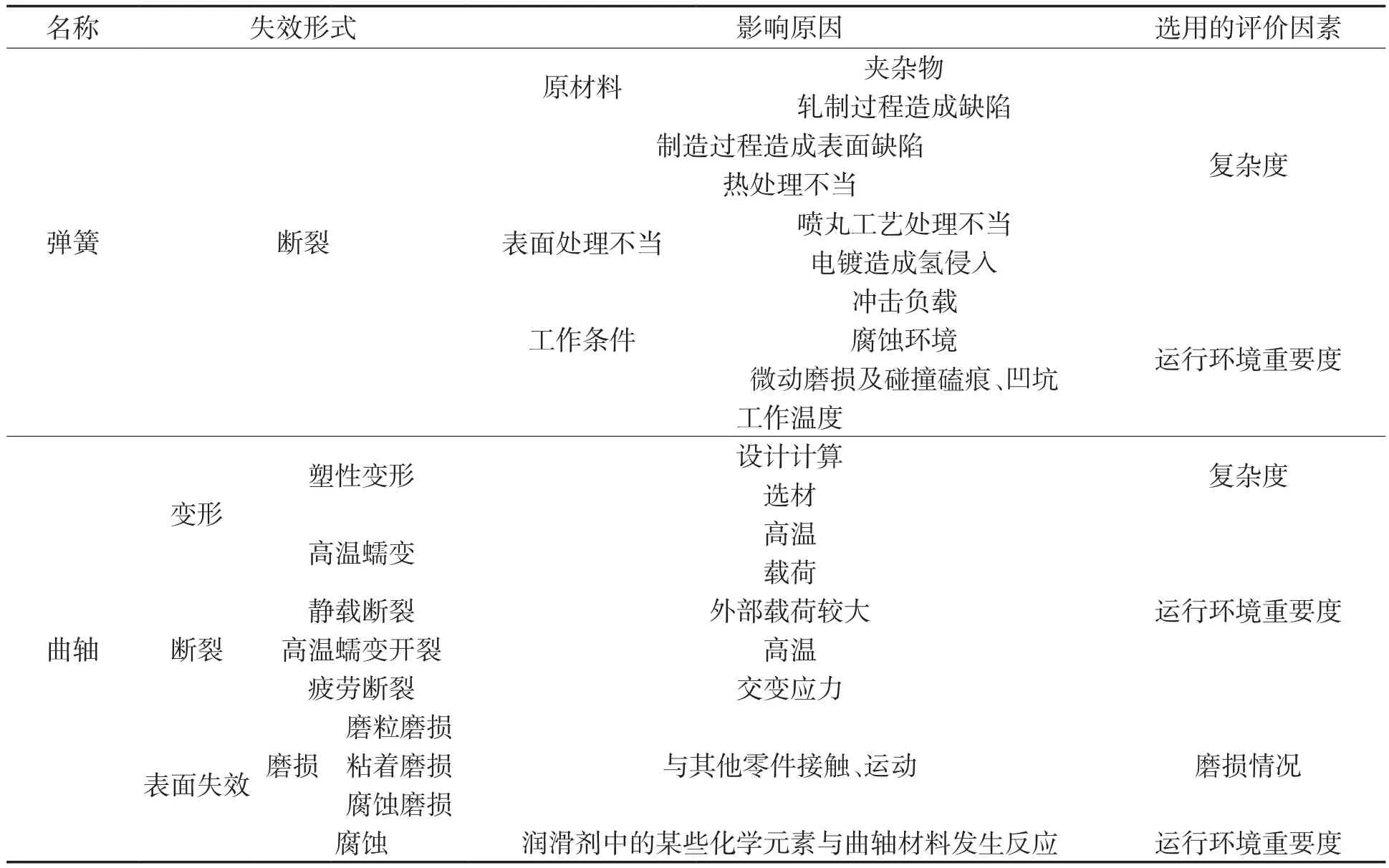
表4 主要零部件失效及评价因素分析Tab.4 Failure analysis of main components and evaluation factors

在进行可靠性分配时，某些部件的结构简单，运行环境重要度、复杂度、磨损情况评分非常低，由此分配的可靠度非常高，认为在压缩机运行期间不会发生故障，在后续可靠度分配时设其可靠度为1，如消声器、阀铆钉。

2.4.2 泵体系统可靠性分配与分析

根据评分分数不同，分配的可靠度也会有所差异。图6中实线为各部件可靠度随评价系数变化情况。随着评价系数增大，部件可靠度减少，可靠度函数曲线呈下降趋势，这说明得分越高，评级系数越大，各影响因素对可靠性产生的影响越恶劣，所分配的可靠度就会越低。不同分配情况下，部件分配的可靠度也随着评价系数的增大而降低。图6中虚线为气缸在5种分配方案下可靠度与评价系数的关系，随着气缸的评价系数从0.171 429增加到0.315 789，气缸分配的可靠度从0.999 76下降到0.999 558。

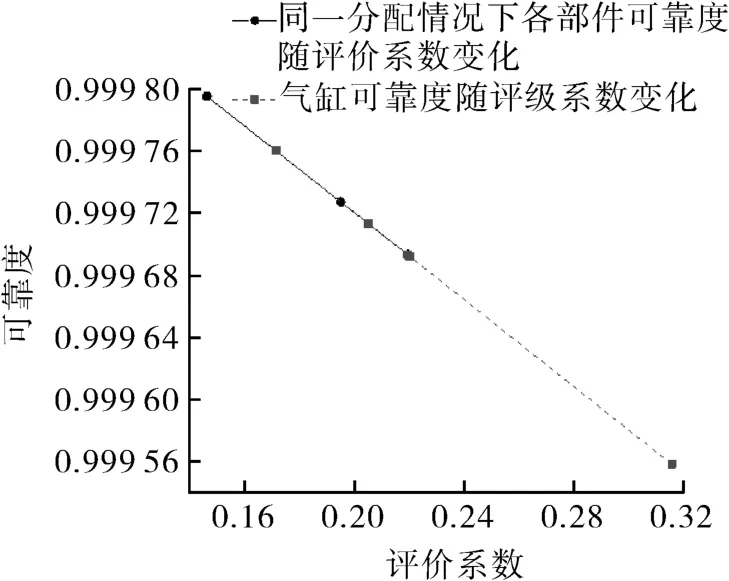
图6 可靠度随评价系数变化Fig.6 Variation of reliability with evaluation coefficient

各种评分方案下泵体系统可靠度与评价总分的关系如图7中实线所示，随着泵体评价总分增加，可靠度随之增加，且大于设计目标0.998 6，说明部件的评分高低不仅影响自身的可靠度分配值，也会对系统整体可靠度产生影响。在总分120～164之间，泵体可靠度的增加发生了跃变，这是因为随着总评分增大，相应初投资也增加，超出设计目标的过度设计越多，对应可靠度的增长也会加快。

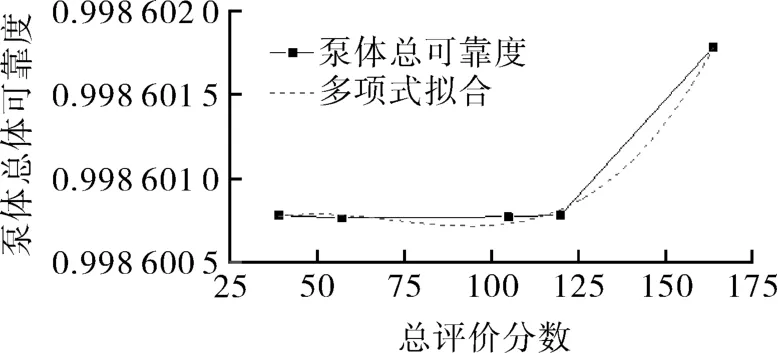
图7 泵体可靠度随总评分变化Fig.7 Variation of pump body reliability with total score

2.4.3 最佳可靠度分配

由上述分析可知，泵体系统可靠度随总评分增大而增大。但随着可靠度的提高，不仅初期投资会增加，而且也会出现过度设计的现象。故在保证可靠度满足要求的前提下，应选取适当的评价分数，达到最佳的可靠度分配，此时成本降低，零部件结构尺寸设计也满足要求。

对泵体总可靠度-评价分数进行多项式拟合，可得到图7虚线，拟合公式为y=0.998 6+2.230 65×10-8x-3.431 01×10-10x2+1.591 14×10-12x3，x 为评价分数，y为泵体系统可靠度。由划分标准可知，评价总分最低为5分，即每个影响因素评价分为1，此时泵体总体可靠度为0.998 6；最高分为320，每个影响因素评价分为4，泵体总体可靠度为0.998 624，都能满足设计要求总体可靠度0.998 6。在材料相同时，目标可靠度R越高，对应的Z值就会越大，代入相应联结方程后求得尺寸就越大。在高、低分评价方案都能够满足设计要求的情况下，若选取最高评分的方案，对零部件的设计以及制造精度都提出更高的要求，就会造成尺寸设计大、精度高的过余设计。这不仅增加了初期投资，而且造成了资源浪费。而最低评分的方案则刚好满足可靠度设计要求，不会过度设计。故在评分与产品实际情况相符的情况下，评分最低的可靠度分配方案是泵体系统的最佳分配方案。

3 结语

（1）根据转子式压缩机的工作特点与结构，可将其划分为7个子系统，对转子式压缩机、泵体系统建立可靠性模型，可知压缩机组成系统、泵体组成部件间均为串联关系。

（2）考虑压缩机频率对与转速相关部件可靠性的影响，引入当量运行时间概念，将不同频率下开机时间折算为额定频率下的当量运行时间。对5个不同地域典型城市的分析表明，最不利条件下的当量运行时间为1 777 h/a（取整为1 800 h/a），发生在海口。

（3）采用重要度和复杂度分配法、评分分配法对压缩机整机、泵体系统进行可靠性分配。在10年18 000 h、可靠度0.99的情况下，泵体系统可靠度为0.998 6，为进一步的研究分析奠定基础。

（4）基于泵体系统5种分配方案分析不同评分情况下泵体系统可靠度、各组成部件可靠度变化，可知随着评分增高，评价系数增大，曲线呈下降趋势，泵体可靠度、部件所分配的可靠度越低，评价因素对可靠度产生的影响越恶劣。

（5）由拟合的泵体可靠度随评价分数变化曲 线 y=0.998 6+2.230 65×10-8x-3.431 01×10-10x2+1.591 14×10-12x3可知：在满足可靠性要求情况下，选取低评价分数方案可达到最佳分配、避免过余设计，减少投资而降低成本。