加速多标签特征提取的内核依赖最大化

邱 劲

（苏州科技大学 电子与信息工程学院，江苏 苏州215009）

多标签分类近年来在图像自动标注[1]、多主题文档分类[2]和蛋白质功能预测[3]等各种应用中受到了广泛的关注。与传统的单标签分类（每个实例只属于一个类别）不同，多标签分类解决每个实例可能与多个类关联的问题。文献中已经给出了大量的算法。现有的方法大致可以分为两类：算法自适应和问题转化[4]。算法自适应法尝试扩展现有的单标签分类算法来处理多标签问题。典型示例包括神经网络[5]、惰性学习[6]、Adaboost MR[7]、秩SVM[8]。对于转化法，通常将多标签分类问题转化为多个单标签分类问题，以便可以轻松使用现有的单标签方法。显著的示例包括二元相关性法[9]、成对法[10]和标签嵌入法[11]。

但是多标签分类经常涉及高维数据，这使得现有方法由于维数问题而变得难以实现。在文献中已经给出了大量的多标签降维方法。如在文献[12]中提出了多标签信息隐形语义索引（MLSI），用于多标签降维。多标签信息隐形语义索引（MLSI）使用标签信息来指导转换的学习，并已成功应用于多标签文本分类。文献[13]将经典线性判别分析拓展至处理多标签数据样本。但是这并没有将标签相关性考虑在内。文献[14]中提出了一种新型多标签线性判别分析（MLDA），其利用标签相关性并探索强大的辨别能力以处置多标签DR。文献[15]中则提出了一种基于依赖最大化的多标签降维方法（MDDM）。该多标签降维方法使用希尔伯特-施密特独立性准则（HSIC）来获取特征描述和相关标签之间的强依赖性。但MDDM需涉及到广义特征值分解，这使得其对于高维数据的计算成本大大增加。上述问题表明多标签特征提取方法通常需要解决一个特征值问题且该问题计算量非常大。因此近年来很多学者对多标签特征提取中的可扩展性问题进行了相关研究。文献[16]中的作者给出了一类广义特征值问题的最小二乘公式并采用共轭梯度算法来提高训练进程。具体而言典型相关分析和核典型相关分析已重新表示为最小二乘问题，但kMDDM的最小二乘公式仍然是一个未解决的难题。因此在文中制定了一种有效解决kMDDM的算法-kMDDM的等效最小二乘公式用以降低计算成本。简言之，本文的主要贡献有以下三点：首先，证明了kMDDM可以重新表示为一个最小二乘问题，基于这种等价关系可通过共轭梯度算法有效推导出kMDDM的解；其次，在多个基准数据集上进行了大量试验用以证明所提出的公式的有效性；最后，将有效的正则化技术合并至最小二乘框架用以提高泛化性能。

1 基于最小二乘法的有效kMDDM

1.1 最小二乘kMDDM

为了有效地计算kMDDM，需使用以下定理。

定理1设b为特征问题的特征向量

特征值为λ。如果Kp=b，则p是具有相同特征值λ的特征问题的特征向量。

证明 将Kp=b代入式（1），得到

定理1表明在不求解特征问题时，式（1）的解可以通过以下两个步骤得到:第一步，求解特征问题（1）得到b；第二步，求出满足Kp=b的p。

在实践中，线性方程Kp=b可能不成立，转而考虑以下最小二乘问题

由于K通常是对称正定的，因此基于共轭梯度的迭代算法可用于求解最小二乘问题（3）。在实施过程中使用LSQR算法来求解稀疏线性方程组和稀疏最小二乘。

上述步骤表明，kMDDM可以重新表示为一个最小二乘问题，此方法被称为最小二乘kMDDM（LSkMDDM）。

然后开始解决特征值问题（1）。令Q＝HY∈Rn×c，从而得到

然而，矩阵QQT的大小为n×n，这对于直接寻找特征值及其相关向量是很难的。因此利用下面的引理并采用一种计算可行的方法来解决这个问题。

引理1如果矩阵QTQ有一个特征值对其中vk是对应于特征值σk的归一化特征向量，那么矩阵QQT有一个特征值对是对应于特征值σk的归一化特征向量。

上述引理表明，为了得到大n×n矩阵QQT的特征系统，可以求解需要较少计算成本的小c×c矩阵QTQ的特征系统。

以LSkMDDM的计算成本分析来结束本节。LSkMDDM需要求解特征问题（1）和最小二乘问题（3）。特征问题的计算需要3/2nc2+9/2c3flam，其就n而言具有线性时间复杂度。对于最小二乘问题，LSQR的每次迭代需要2n2+8n。由于最小二乘求解c次，所以LSQR的总成本为Tc（2n2+8n），其中T是迭代次数。因此，LSkMDDM的总时间复杂度为3/2nc2+9/2c3+Tc（2n2+8n）。考虑到c＜＜n，时间复杂度可以改写为2Tcn2+O（m）+O（n），比原公式小得多。

1.2 LSkMDDM拓展

基于kMDDM和最小二乘法之间的等价关系提出了LSkMDDM的两种泛化。

首先，考虑使用正则化技术来控制复杂性并提高泛化性能。一种常见的正则化项是在p上加上l2范数，为此提供了以下正则化的LSkMDDM（称为rLSkMDDM）

其中，η＞0是一个权衡参数。这种正则化在机器学习中得到了很好的研究，称为岭回归[17]。通过将右侧关于p的导数设置为零，得到

最后，得到了一个闭式解

此外，正交约束也可以合并到kMDDM的最小二乘公式中，从而得到以下表达式

其中，B是n×c矩阵，其列是（1）的特征向量。约束条件形成一个Stiefel流形，导致了矩阵流形的一个典型优化问题[18]。经典的牛顿算法和共轭梯度算法可以拓展到Stiefel流形上来处理这类问题。

2 试验结果及分析

2.1 试验装置

首先使用场景和酵母数据集来验证kMDDM和LSkMDDM之间的等价关系[19－20]。同时，利用Yahoo数据集、pascal07和RV1三个高维数据集来进一步验证最小二乘模型的有效性。这些数据集的重要统计数据如表1所列。

表1 数据集统计汇总

使用由高维网页构成的多主题网页分类数据集（表示为Yahoo）来验证提出的模型的有效性。Yahoo数据集如表1所述，其由14个顶级类别（即“艺术与人文”、“社会与教育”等）构成。顶级类别进一步分为多个二级子类别，这些子类别构成了每个数据集中分类的主题。RCV1数据集包含来自路透社的新闻专线报道。该数据集的处理方法是删除停止词、词干提取并将文档转换为TF-IDF格式的向量。在试验中使用了一个包含6 000个示例的子集，其中3 000个示例用于训练，其余的用于测试。

Pascal07数据集包含20个不同对象类别的9 963个图像。本文使用标准训练/测试分区来评估所提出方法的性能，有5 011张图像用于训练，4 952张图像用于测试。

对于表1中前两个相对较小的数据集，从3个随机分区中选择2个作为训练集，其余的作为测试数据。对于Yahoo数据集，其被分成两部分：一个包含4 000个样本的训练集和一个包含剩余样本的测试集。接下来，重复分区过程10次并报告平均结果。

试验中用到的五种算法总结如下：

·KPCA：主成分分析的非线性拓展。KPCA是一种无监督的方法。

·KCCA：核典型相关分析在试验中采用了更有效的KCCA的最小二乘公式。

·LSkMDDM：kMDDM的最小二乘公式。

·rLSkMDDM：正则化LSkMDDM。

·OLSkMDDM：正交LSkMDDM。这里使用文献[21]中提出的算法来推导OLSkMDDM的解。

在实施过程中采用了高斯核函数，其中核的标准偏差等于数据点之间成对欧氏距离的中值。

利用上述算法可得到一个变换矩阵并将每个测试样本映射到一个低维空间。接下来将低维空间的维数设置为c（标签的数量），然后采用多标签k-最近邻分类器 来预测测试样本的标签[22]。

其次，使用七种标准来评价多标签学习算法的性能。第一组评价标准包括macro F1和micro F1，它们与每个实例的标签集预测性能有关。设f是一个分类器函数，f（xi）是由f预测的二元标签向量。两个评价指标定义如下

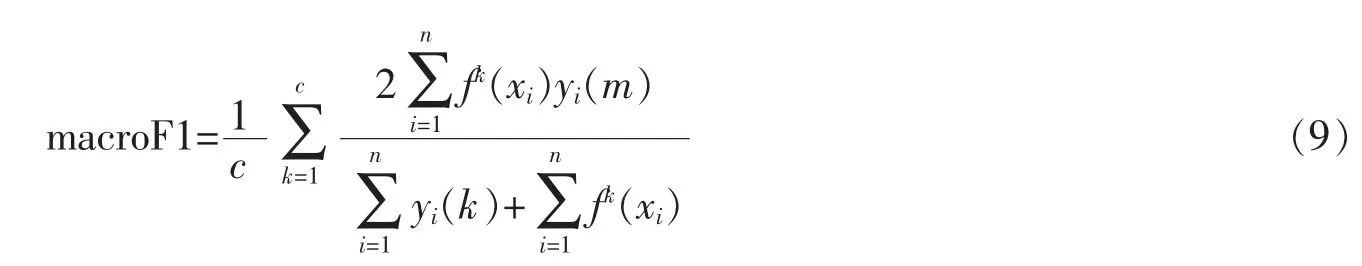
其中，yi是真二元标签向量，例如xi，yi（k）是yi的第k个元素，fk（x）是f（x）的第k个元素。

请注意，这两个值越大，性能越好。

第二组评价标准包括排名损失（RL）、一次误差、覆盖率和平均精度（AP），与标签排名性能有关。这些标准的详细说明见[23]。还研究了每个标签的ROC曲线下面积（AUC）[24]。将多标签分类视为c个二元分类问题，并计算每个问题的AUC。之后报告所有标签的平均AUC。注意RL、一次误差和覆盖率的值越小，而AP和AUC的值越大时，性能越好。

2.2 kMDDM和LSkMDDM性能分析

首先评估kMDDM和LSkMDDM的等价关系。其中表2描述了kMDDM和LSkMDDM在AUC和两个F1分数方面的性能。由表2可知kMDDM和LSkMDDM具有相似的性能这与文中的分析结果高度一致。

表2 场景和酵母数据集的kMDDM和LSkMDDM三方面性能

Yahoo数据集在AUC、macroF1和microF1方面的试验结果报告如表3和表4所列。

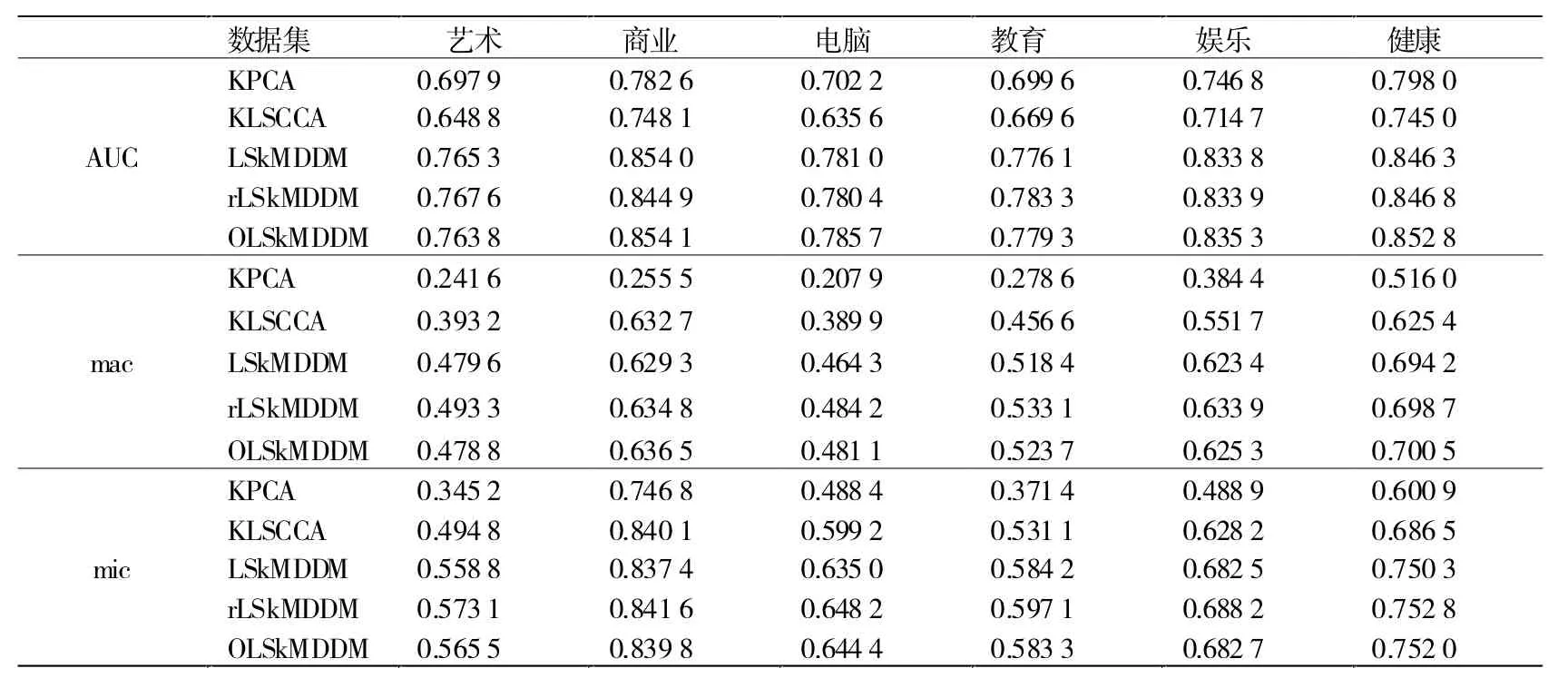
表3 关于前六个数据集的七种比较算法在AUC（顶部）、macro F1（mac）和micro F1（mic）方面的性能

表4 关于五个数据集的七种比较算法在AUC（顶部）、macro F1（mac）和micro F1（mic）方面的性能

由表3和表4可知，KPCA取得了比KLSCCA更高的AUC，而KLSCCA在macroF1和microF1方面的性能优于KPCA；kMDDM和rLSkMDDM都依赖于HSIC并取得了比KPCA和KLSCCA更好的性能。这表明HSIC在处理高维多标签样本时的优越性；无论数据集如何，rLSkMDDM在所有数据集上都实现了microF1的最高性能。此外，rLSkMDDM在九个数据集中的macro F1得分最高，而OLSkMDDM在其余两个数据集上的得分最高。这些观察结果表明，通过结合正则化技术和正交约束，可以显著提高kMDDM最小二乘公式的性能。有趣的是，在所有数据集上，rLSkMDDM和OLSkMDDM在AUC方面取得了相当相似的性能。

表5 至表7报告了Yahoo、pascal07和RCV1数据集在RL、一次误差、覆盖率和AP方面的结果。结果也很理想。从表5和表6中可以看出，无论标准如何，rLSkMDDM在八个数据集上都实现了最高性能。此外，可以看到OLSkMDDM在pascal07数据集上实现了最佳性能，而rLSkMDDM就RCV1数据集在RL、覆盖率和AP分数方面取得了更好的性能。

表5 关于前六个数据集的七种比较算法在RL、一次误差、覆盖率和AP方面的性能

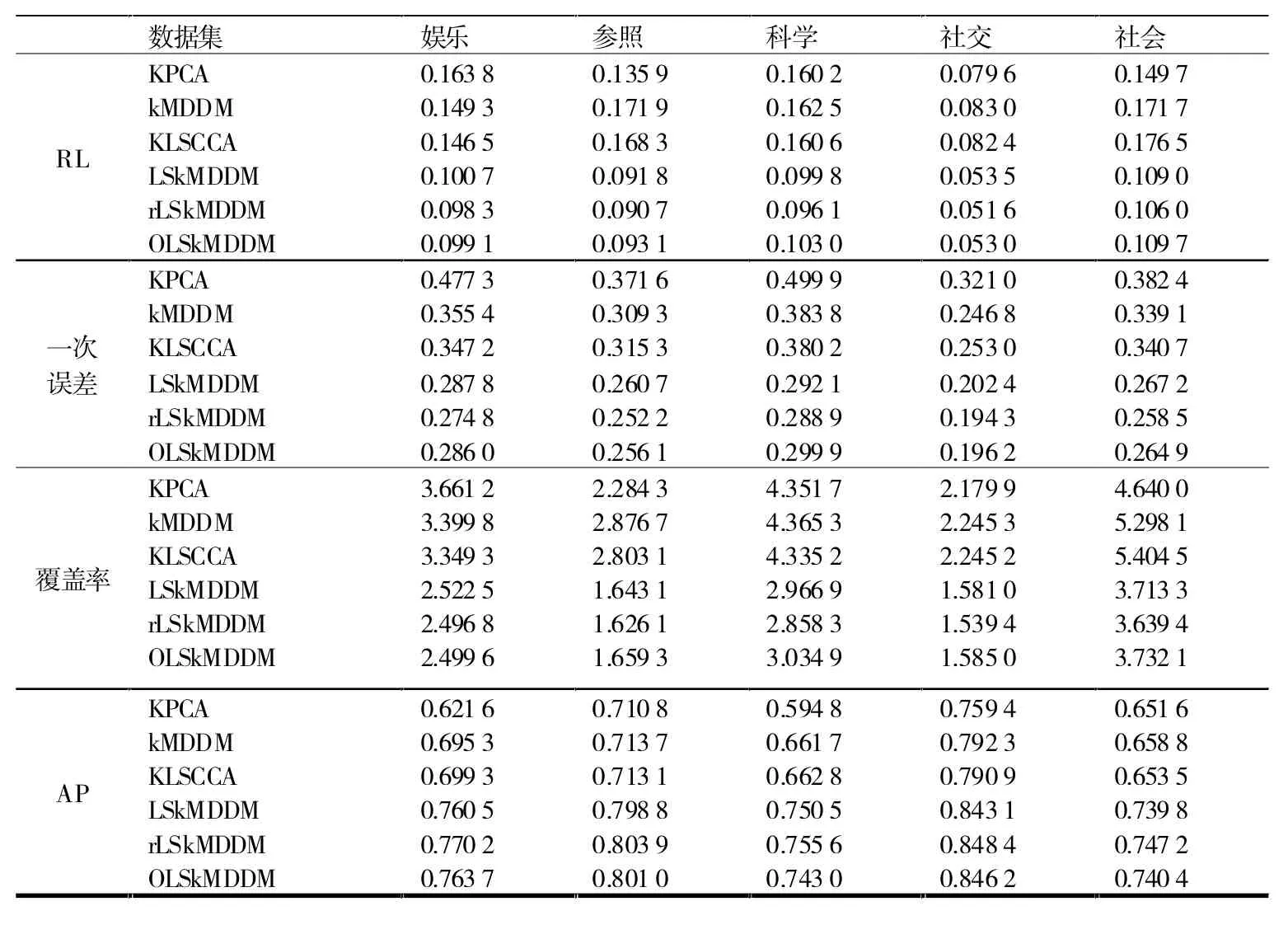
表6 关于五个数据集的六种比较算法在RL、一次误差、覆盖率和AP方面的性能

表7 pascal07和RCV1的试验结果

2.3 降维数的影响

使用Yahoo数据集来测试维度对分类性能的影响。首先从Yahoo中选取了四个高维数据集，并用不同的降维方法对其性能进行了评估。图1至图3描述了不同降维条件下AUC、macro F1和micro F1的性能。可以观察到，随着维数的增加，所有比较方法的性能都有所提高。特别是，rLSkMDDM和OLSkMDDM往往比其他方法取得更好的性能。

图1 不同维度的AUC值

图3 不同维度的微观F1值

2.4 可扩展性评估

在本试验中，比较了原MDDM与第2.1中给出的MDDM最小二乘公式（LSkMDDM）的可扩展性。除了基于SVD的kMDDM方法外，还使用免逆预处理Krylov子空间方法]来求解kMDDM的原始特征值问题。具体而言，从Yahoo中选择了四个数据集并通过将训练集的大小从500改到2 000来估计kMDDM和LSkMDDM的计算时间，其他数据集也可以观察到类似的趋势变化。

计算时间如图4所示可以看出，当训练集的大小固定为500时，所有方法的时间复杂度大致相同。然而，随着训练集规模的增大kMDDM的时间复杂度远高于kMDDM-ifp和LSkMDDM。此外，很容易看出最小二乘kMDDM可以进行大规模应用。

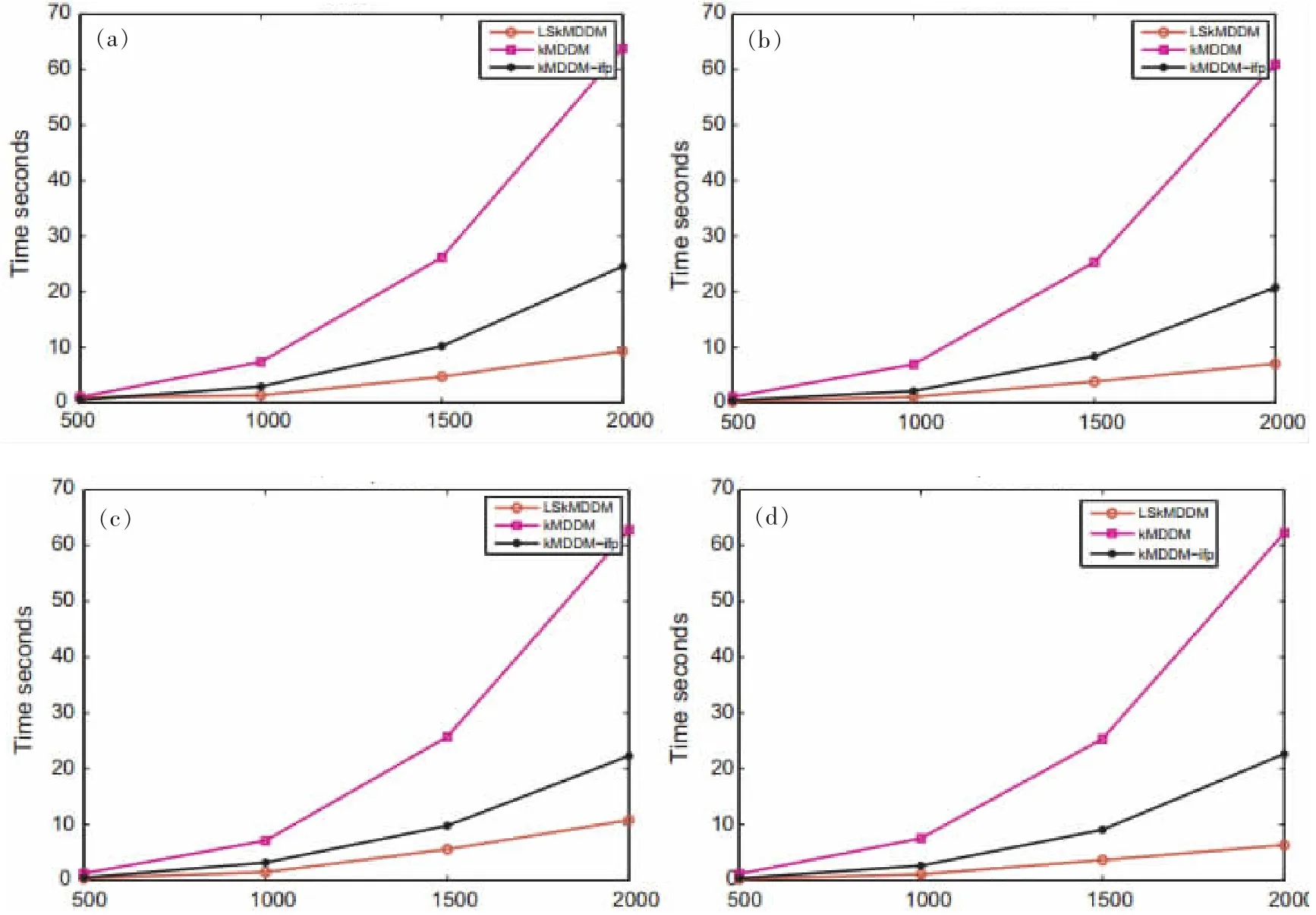
图4 随着样本量的增加，LSkMDDM、kMDDM和kMDDM-ifp在艺术、商业、电脑和教育数据集上的计算时间比较

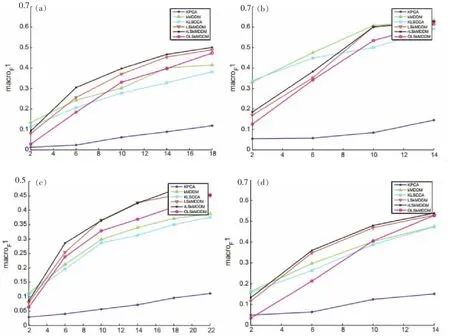
图2 不同维度的macro F1值

3 结论

本文研究了用于多标签特征提取的高效kMDDM问题。基于kMDDM与其最小二乘公式之间建立的等价关系可以采用迭代共轭梯度算法来显著降低原kMDDM的计算成本。此外一些前景很好的技术（如l2-范数）可以很容易地合并到新的最小二乘公式中从而显著提高泛化性能。基准数据集的试验结果证明了所提出公式的有效性和效率。