深海矿产矿浆泵矿石颗粒回流性能

关英杰， 邹丽， 郑皓， 边有刚， 于宗冰

(1.湖南大学 机械与运载工程学院，湖南 长沙 410082； 2.大连理工大学 船舶工程学院，辽宁 大连 116024； 3.长沙矿冶研究院有限责任公司 深海矿产资源开发利用技术国家重点实验室，湖南 长沙 410012； 4.清华大学 水利系， 北京 100084)

随着陆地矿产资源的衰竭，深海矿产资源开发技术也越来越被世界各国所重视[1]，目前最有商业开采前景的开采方案是管道提升法[2]。扬矿泵作为采矿系统中最核心的动力装备，世界各国都进行了大量研究，德国KSB公司[3]开发的扬矿泵存在过流部件磨损严重，韩国Cundall等[4-5]开发的扬矿泵存在局部颗粒堵塞的情况，日本学者[6]开发的多级扬矿泵停泵后矿浆无法顺利回流，我国长沙矿冶研究院[7-8]开发的扬矿泵在实验过程中也出现了回流堵塞。目前国内开发的扬矿泵过流和回流能力往往不足，导致流道堵塞。采矿系统正常关闭时，矿浆的输送将会提前停止，停泵时输送系统内无矿浆，不存在堵塞问题。而采矿系统在实际开采过程中，船舶的电力供应相对陆地来说不是很稳定，因此矿浆泵存在一定断电紧急停泵风险。在紧急停泵后，水下系统内两相流经短暂波动，其运动状态将趋于稳定，矿物颗粒在重力作用下向海底自由沉降下落。在沉降回流过程中一旦发生堵塞，整个采矿系统将无法重新工作，因此对于颗粒回流过泵通过性的研究具有重要意义。目前我国海试用矿浆泵具有较好的正向流动防堵塞性能，矿浆泵采用多级叶轮-空间导叶的布局，通过放大流量的思路进行水力设计[9-11]。众多学者通过试验和数值模拟分析了颗粒体积分数、流量、转速等参数对矿浆泵的外特性的影响规律。针对深海采矿矿浆泵流动特点[12-16]，Zhou等[17]提出了一种基于无量纲方法和突变理论定量研究湍流相变的新方法，对泵内固液两相流动进行了分析。Tan等[18]采用高速摄影技术，对双叶片深海采矿泥浆泵内粗颗粒固液两相流中单颗粒的运动规律进行跟踪，分析了粒子直径和粒子密度对粒子通过和碰撞特性的影响。Ma等[19]通过Fortran和Matlab环境下的数值模拟和配件模拟，研究了离心泵的建模和工作原理，确定了最优效率、总能耗、输运损失因子和相关开采参数之间的关系。文献[20-21]采用不同粒径，不同浓度的模拟结核在两级矿浆泵进行了实验，测试了某型矿浆泵的回流能力。数值模拟相对于实验研究可以更加好的发现泵内的堵塞细节，分析堵塞机理，目前还鲜有运用数值模拟方法对泵回流能力方面研究的发表。为此，本文采用CFD-DEM耦合算法，考虑了颗粒的体积效应和碰撞作用以及不同颗粒形状，对矿浆泵的回流情况进行数值模拟，分析矿浆泵的回流堵塞原因，为可回流矿浆泵的设计提供理论依据。

1 模型与方法

1.1 矿浆泵回流理论分析

采矿系统回流过程如图1所示，矿浆泵下方管道内的矿浆颗粒将在管道内自由沉降，基本无回流堵塞风险，而矿浆泵上方管道内的矿浆颗粒将通过矿浆泵回流到海底，在矿浆泵内存在一定的堵塞风险。回流过程中，颗粒群在流道内贴着泵体表面滑动，在导叶流道内沿着导叶叶片和导叶前盖板流动，在叶轮流道内沿着叶轮叶片和叶轮前盖板流动。泵的回流能力与叶轮导叶的子午面形状和叶片的包角有关，在叶轮导叶叶片数相同的情况下，叶轮和导叶子午面形状与水平线的角度越大，颗粒在轴向方向的回流情况越好，矿浆泵流道子午面形状如图2所示，相对叶轮流道，导叶子午面形状与水平线的角度更大，导叶流道回流情况要好于叶轮流道，泵的过流能力主要决定于叶轮的形状。

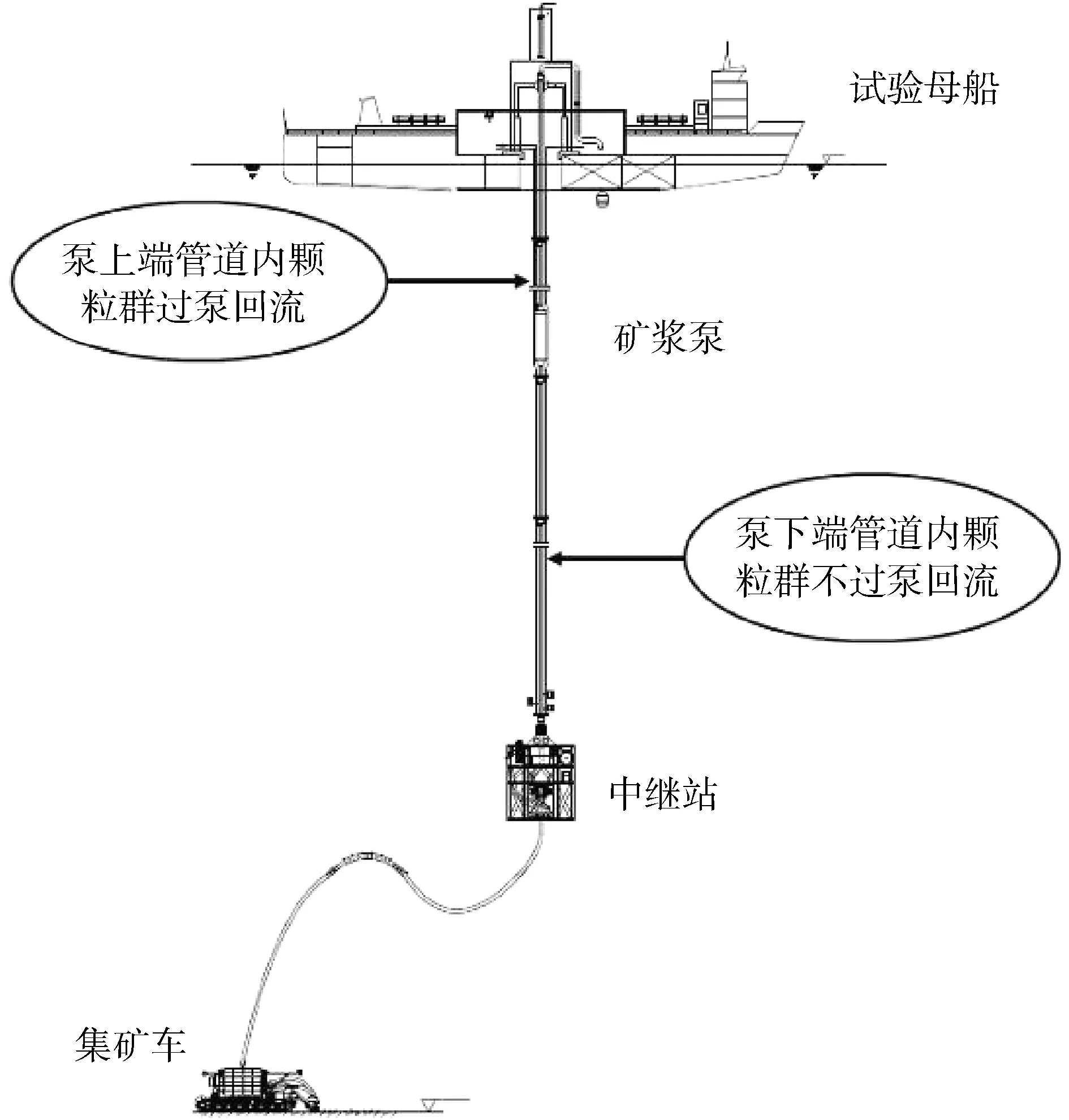
图1 采矿系统及紧急停泵后矿浆回流示意Fig.1 Mining system and reflux after emergency stop of pump

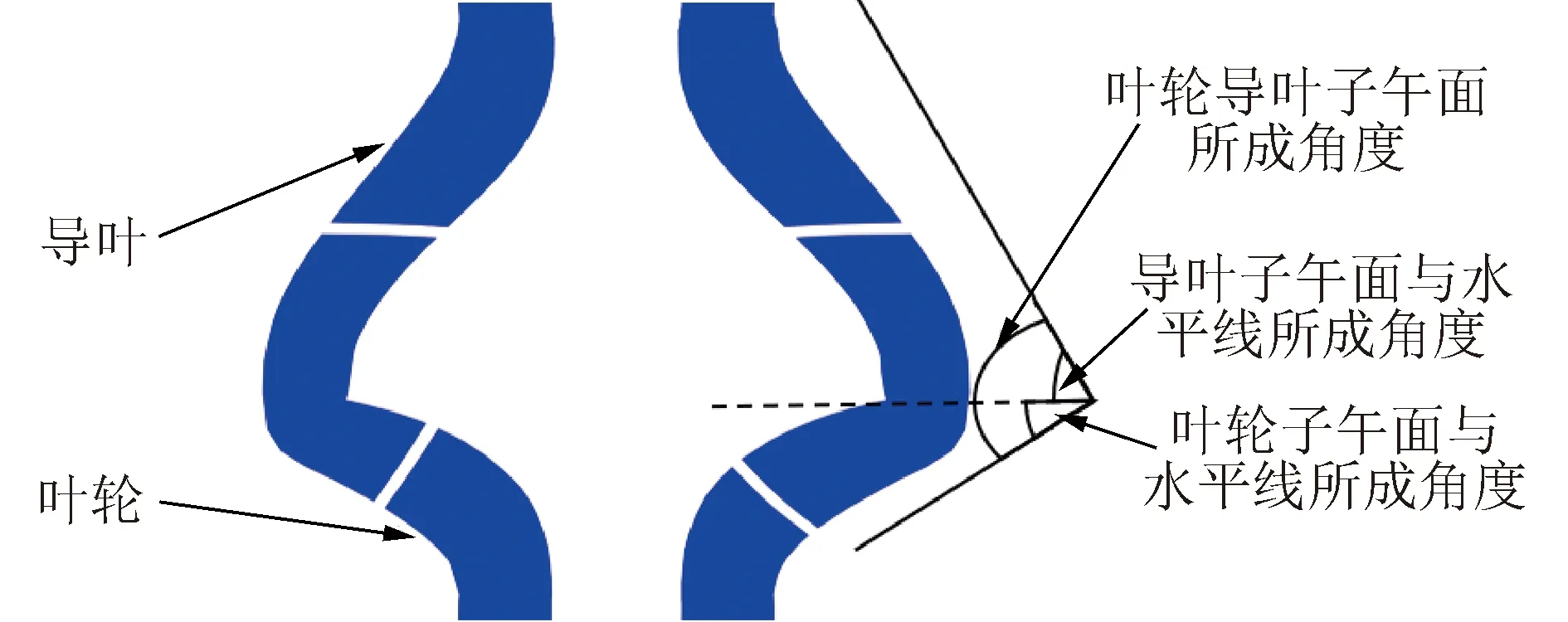
图2 泵叶轮导叶轴面图Fig.2 Pump axial surface diagram

颗粒在叶轮流道内的流动轨迹可以分为轴向方向和径向方向，如图3所示，轴向方向的流动长度与叶轮的轴面投影有关，径向方向的流动长度与叶轮的平面投影形状有关。如图4所示，叶轮轴面投影形状与泵的比转速有关，低比转速叶轮窄而长，高比转速叶轮宽而短，颗粒在高比转速泵叶轮流道内回流时，流动距离短，更有利于颗粒的回流。颗粒在径向方向上的流动距离与叶轮叶片的型线有关，如图5所示，颗粒在型线3的叶轮内流动距离短，更容易回流，即小包角的叶轮叶片具有更好的回流性能。

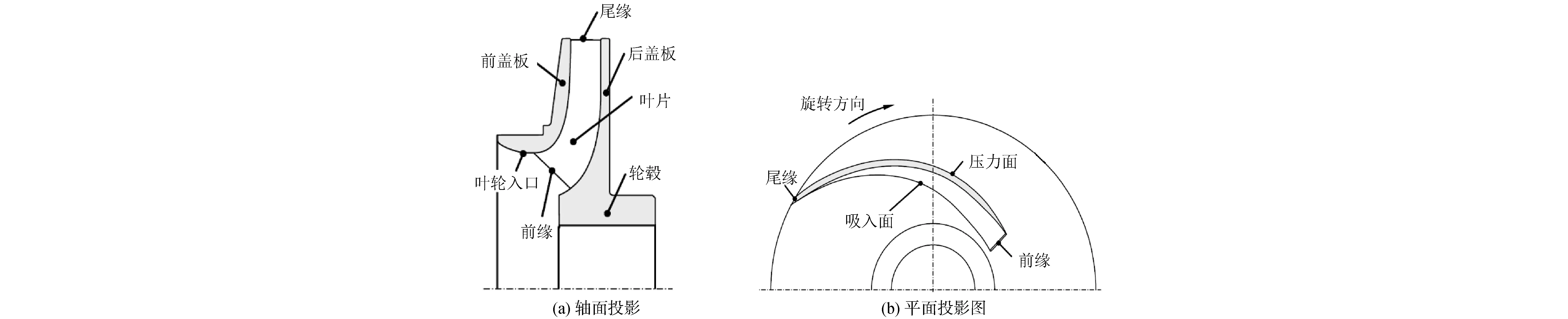
图3 叶轮轴面投影图和平面投影Fig.3 Meridional section and plan view of a impeller

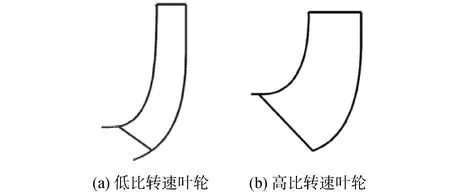
图4 不同比转速叶轮形状Fig.4 Impeller shape of different specific speed

图5 不同叶轮工作面型线Fig.5 Different profiles of blade working surface

1.2 CFD-DEM耦合算法

CFD-DEM耦合算法的求解策略由CFD求解器求解连续相，由DEM求解器求解离散相，所以CFD-DEM求解分为3个部分：连续相求解、离散相求解和两相间的耦合。

流体连续相求解主要应用连续性方程和动量方程(Navier-Stokes方程)。离散相的求解主要是通过接触模型求解颗粒碰撞过程的受力，并运用牛顿第二定律计算出颗粒的加速度，然后更新颗粒的速度和位移。

如图6所示，在每个时间步长中，首先CFD求解器计算连续相流场，仿真迭代至收敛，然后将网格单元的流体条件传递给DEM求解器，从而计算出作用在颗粒上的阻力，并将此力代入颗粒运动方程，求解离散相的位置、速度等信息。DEM迭代计算结束后，估计出计算单元内的孔隙率并连同相间作用力传递回CFD求解器。CFD求解器利用这些数据求解连续相流场，更新流动区域，以此循环进入下一个时间步长[22]。

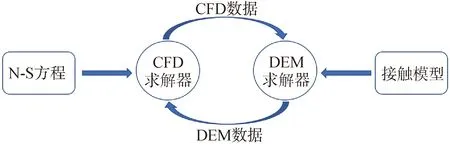
图6 CFD-DEM耦合原理Fig.6 CFD-DEM coupling

1.3 流场计算域及计算参数设置

选取某型6级矿浆泵为研究对象，其基本参数为流量Q=420 m3/h，单级扬程H=45 m，转速1 450 r/min，叶轮叶片数Z1=3，导叶叶片数Z2=4，叶轮外径D2=420 mm，叶轮叶片出口宽度b2=60 mm，导叶进口宽度b3=62 mm。对六级泵进行数值模拟需要巨大的计算资源，对单级和两级叶轮和导叶进行研究足以反应泵的回流能力及颗粒回流运动特征。流场计算区由进口延长段、出口延长段、叶轮和导叶4部分组成，其三维模型如图7(a)所示。回流连续相介质的流动相对简单，对网格的要求不是很高，采用较适合CFD-DEM耦合算法的多面体网格进行数值计算，局部网格如图7(b)所示；DEM算法为无网格算法，DEM计算的时间步长设置为30%的Rayleigh时间步长以内。计算域连续相为静止流体，进出口无流动，颗粒自泵出口射入计算域。对单级和两级叶轮导叶内的单一粒径颗粒回流以及两级叶轮导叶内混合粒径颗粒和非球形颗粒回流进行非定常计算。

图7 计算域实体模型及网格Fig.7 Computational domains and mesh

2 计算结果与分析

2.1 单级叶轮导叶回流

对20 mm粒径体积浓度5%的颗粒群在单级泵内的回流情况进行数值模拟，泵内颗粒群分布情况如图8所示，随着时间增加泵内颗粒数量不断增加。泵内颗粒群总体积随时间的变化曲线如图9所示，泵内的颗粒群总体积虽不断增加，但曲线的斜率逐渐减小，总体积增大的趋势逐渐放缓。当泵流道内的颗粒数逐渐增多时，由于重力的作用，下端颗粒受到上端颗粒的重量压力作用，更容易流动过泵，颗粒相流入流出计算域的速度逐渐接近，泵内的颗粒群总体积趋于稳定。此外，泵内不同导叶流道内的颗粒群塞积情况不同，图10为30 s时刻泵内不同导叶流道内的颗粒分布情况，以图10(a)为泵流道正面视图角度，图10(b)、(c)、(d)分别为将泵顺时针(自上向下观察)旋转90°、180°、270°后的正面视图。出口延长段内的颗粒随机分布，进入4个导叶通道内的颗粒数量基本相同，相同时间不同通道内的颗粒数量不同。将4个导叶流道分别编号，导叶通道4内的颗粒群数量最多，通道2内的颗粒群数量最少，通道1、3内颗粒数量介于两者之间。不同导叶通道与叶片的位置关系如图11所示，4个导叶叶片编号为a、b、c、d，叶轮叶片编号为A、B、C，叶轮流道分别编号为①、②、③，4个导叶流道与图10中的导叶流道编号相同。

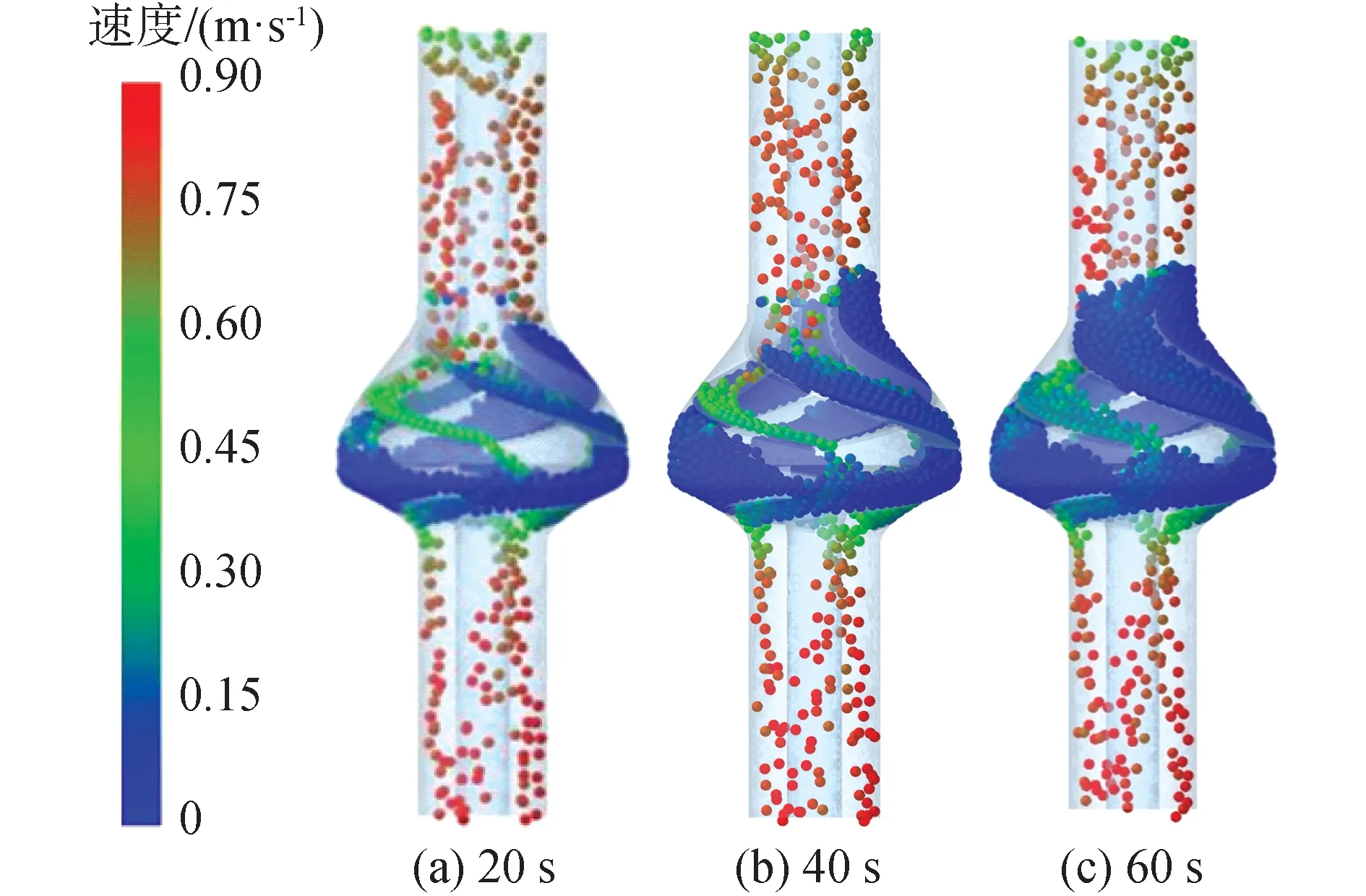
图8 不同时刻单级叶轮导叶内颗粒分布Fig.8 Particles distribution in single stage pump at different moments

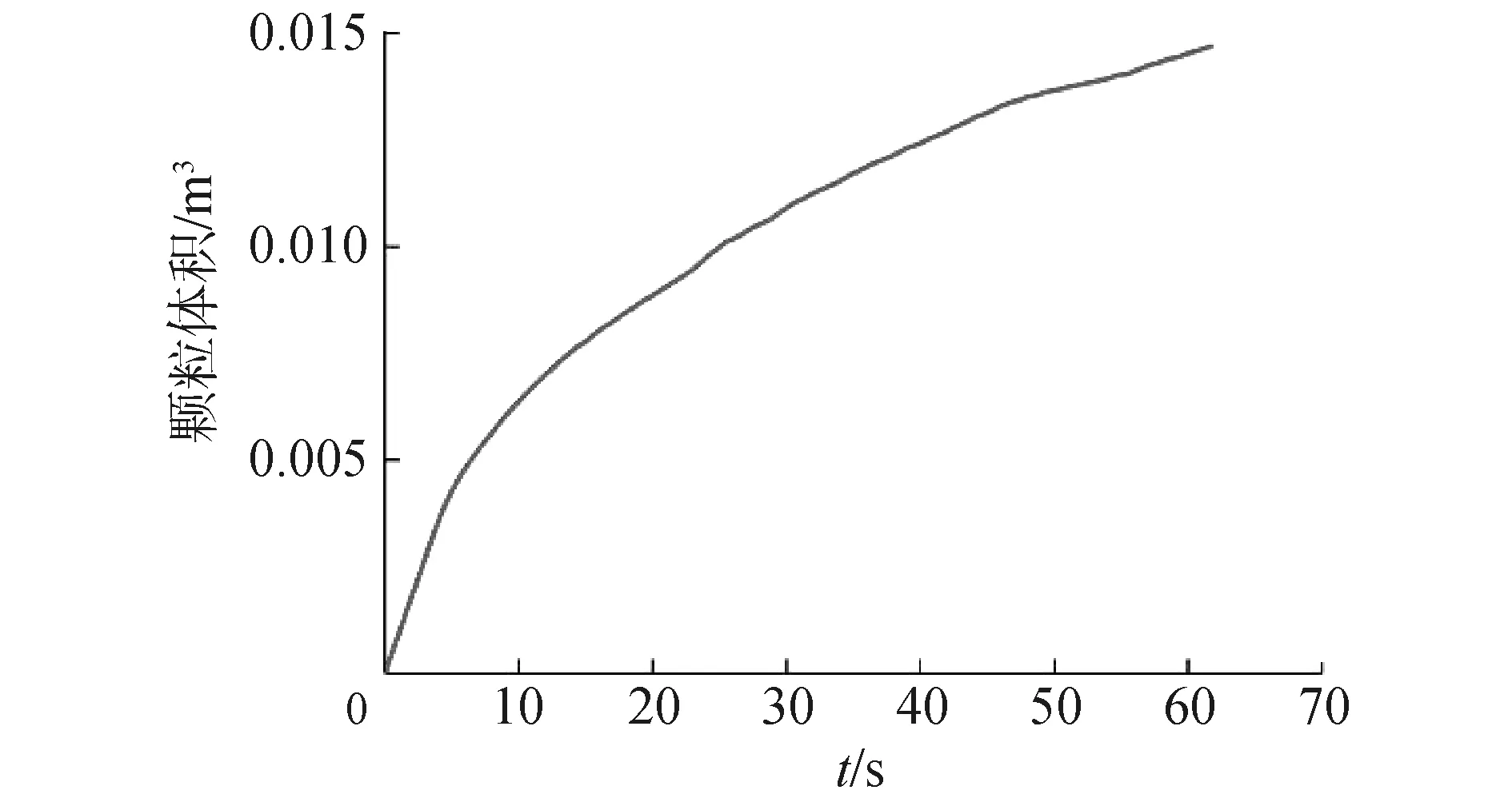
图9 单级叶轮导叶内颗粒总体积随时间的变化Fig.9 variation of particle volume in single-stage pump with time

不同导叶流道内的颗粒群进入叶轮流道后的流动情况不同，导叶流道2内的颗粒群从导叶叶片a表面滑入叶轮流道②内，沿着叶轮叶片A向下流动，颗粒从导叶流道进入叶轮流道后落到叶轮叶片A靠近头部位置，流出泵内的运动距离较短，在叶轮流道②内同时还要通过导叶流道3的少部分颗粒，但对导叶通道2流出的颗粒回流影响并不大，导叶通道3的颗粒主要通过叶轮流道③回流。导叶流道4内的颗粒群从导叶叶片c表面滑入叶轮流道③内，颗粒落到叶轮叶片C靠近尾部位置，但在叶轮流道③内还存在导叶流道3的大部分颗粒，对来自导叶通道4的颗粒回流形成阻碍，颗粒在叶轮流道③出口处滞留塞积后导叶流道4的小部分颗粒流入叶轮流道①，总的来说，导叶通道4的颗粒从叶轮流道①和③回流均会存在较大的阻碍，颗粒在导叶通道4中回流通过性较差。导叶流道1和导叶流道3的回流通畅性介于导叶流道2和导叶流道4之间，导叶流道1内的颗粒进入叶轮流道①后落到叶轮叶片B的靠近尾部位置，同时颗粒从导叶叶片b滑落时带有叶轮叶片B尾部运动的速度，但速度不足以使颗粒沿叶轮叶片B进入叶轮流道②，这一现象导致导叶流道1内的颗粒回流通畅性不如导叶通道2那么好。颗粒在导叶流道3的运动情况刚好与导叶流道1的情况相反，颗粒沿着导叶叶片d滑落时，带有向叶轮叶片A尾部的速度且导叶叶片d尾部与叶轮叶片A尾部的距离很近，大部分颗粒进入叶轮流道③，回流阻碍相比导叶流道4较少。综上，不同导叶流道内颗粒的回流通过性不同，主要是由导叶叶片与叶轮叶片的相对位置决定的。

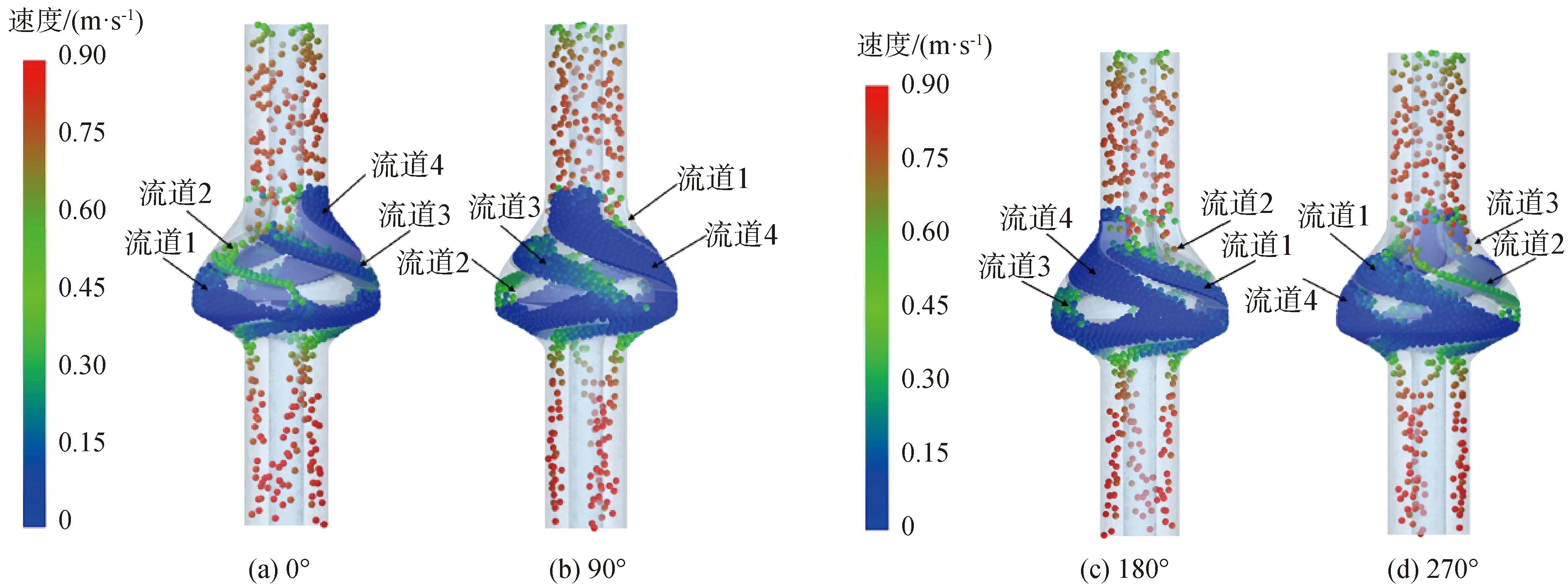
图10 单级叶轮导叶30 s时流道内颗粒群分布Fig.10 Particles distribution in single-stage pump at 30 s

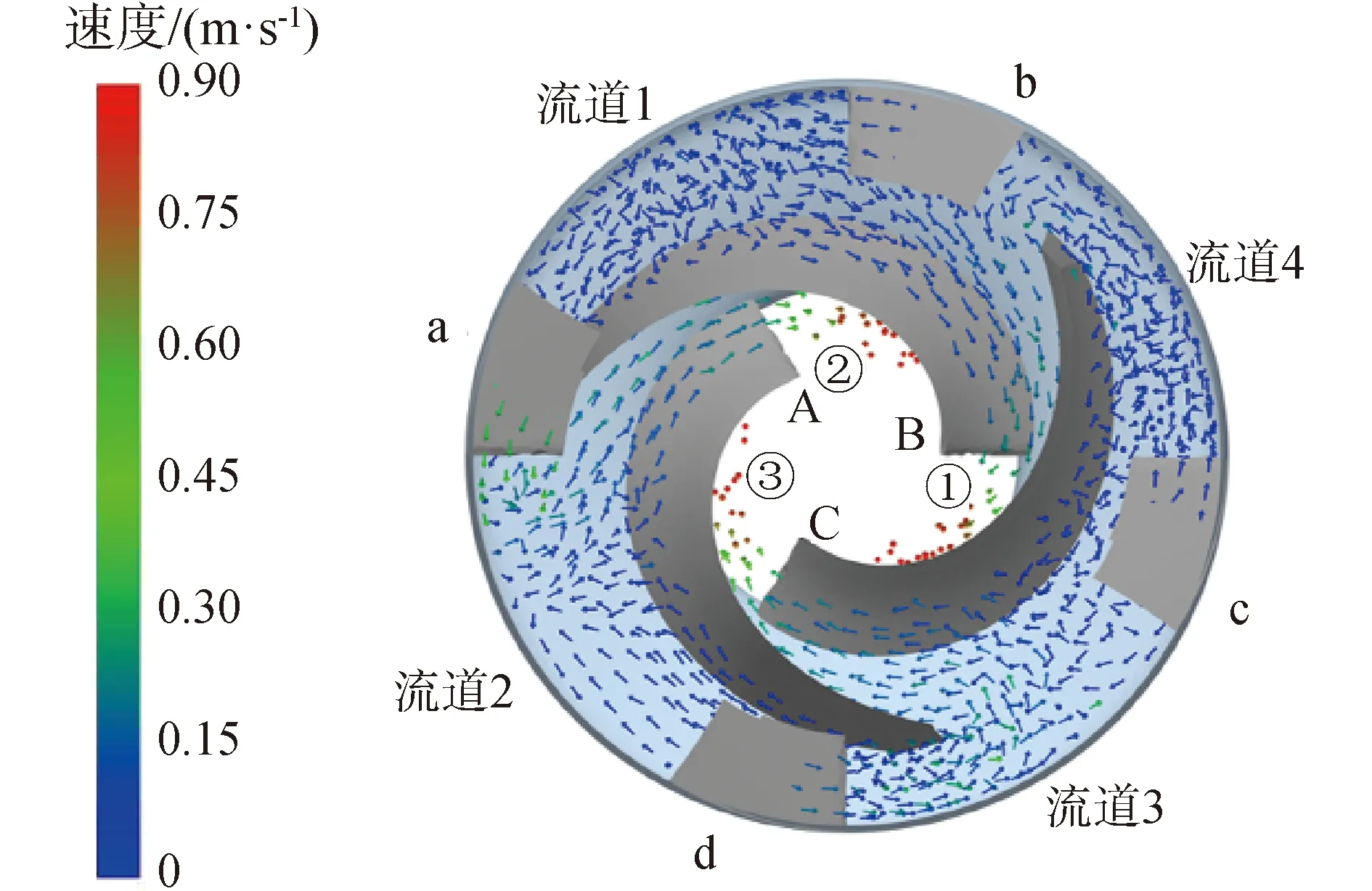
图11 单级叶轮导叶内颗粒速度矢量Fig.11 Particle velocity vector in single-stage pump

2.2 两级叶轮导叶回流

矿浆颗粒在多级泵内回流情况可能与单级泵内的情况不同，矿浆颗粒经过次级叶轮导叶进入首级叶轮导叶时的动能不同，这可能对颗粒在首级叶轮导叶内的回流通过性产生一定的影响，对两级泵内颗粒的回流情况进行数值模拟，可以反应颗粒在多级泵内回流的情况。

对颗粒粒径为20 mm，体积浓度为5%的颗粒群进行两级泵回流数值模拟，泵内颗粒的分布情况如图12所示。泵内的颗粒群总体积随时间变化情况如图13所示，与单级泵相类似，两级泵的颗粒总数也是不断增加，但增多趋势逐渐减缓。同时，首级叶轮导叶内的颗粒总体积变化趋势与次级叶轮导叶内的变化趋势基本一致，证明泵的回流能力不会因为级数增多而发生变化。

图12 两级叶轮导叶内颗粒群分布随时间变化Fig.12 Particles distribution in two stage-pump at different moments

图13 两级叶轮导叶内颗粒总体积随时间变化Fig.13 Variation of particle volume in two-stage pump with time

图14为30 s时泵内不同导叶流道内的颗粒分布情况，以图14(a)为泵流道正面视图角度，图14(b)、(c)、(d)分别为将泵顺时针(自上向下观察)旋转90°、180°、270°后的正面视图，将导叶流道分别编号，在次级导叶流道内颗粒群的分布情况与单级泵一致，导叶通道4内的颗粒数量最多，通道2内的颗粒数量最少，通道1、3内颗粒数量介于两者之间。

图14 两级叶轮导叶30 s时流道内颗粒群分布Fig.14 Particles distribution in two-stage pump at 30 s

在首级叶轮导叶内，受首级叶轮叶片与导叶叶片相对位置的影响，导叶流道6颗粒回流通过性最好，导叶流道8颗粒回流通过性最差，导叶流道5和导叶流道7颗粒回流通过性介于两者之间，但同时，首级导叶内颗粒群分布还受到次级叶轮的影响。次级叶轮叶片与首级导叶叶片的相对位置如图15所示，首级叶轮流道①和叶轮流道②内的颗粒分别沿着叶片B和叶片A分别进入导叶流道5和导叶流道6，而叶轮流道③内的颗粒大部分进入了导叶流道8，少部分颗粒进如导叶流道7。在首级叶轮叶片和次级叶轮叶片的综合作用下，首级泵内导叶流道7内颗粒数量最少，导叶流道6内颗粒数量略多于导叶流道7，导叶流道5和导叶流道8内颗粒数量最多。

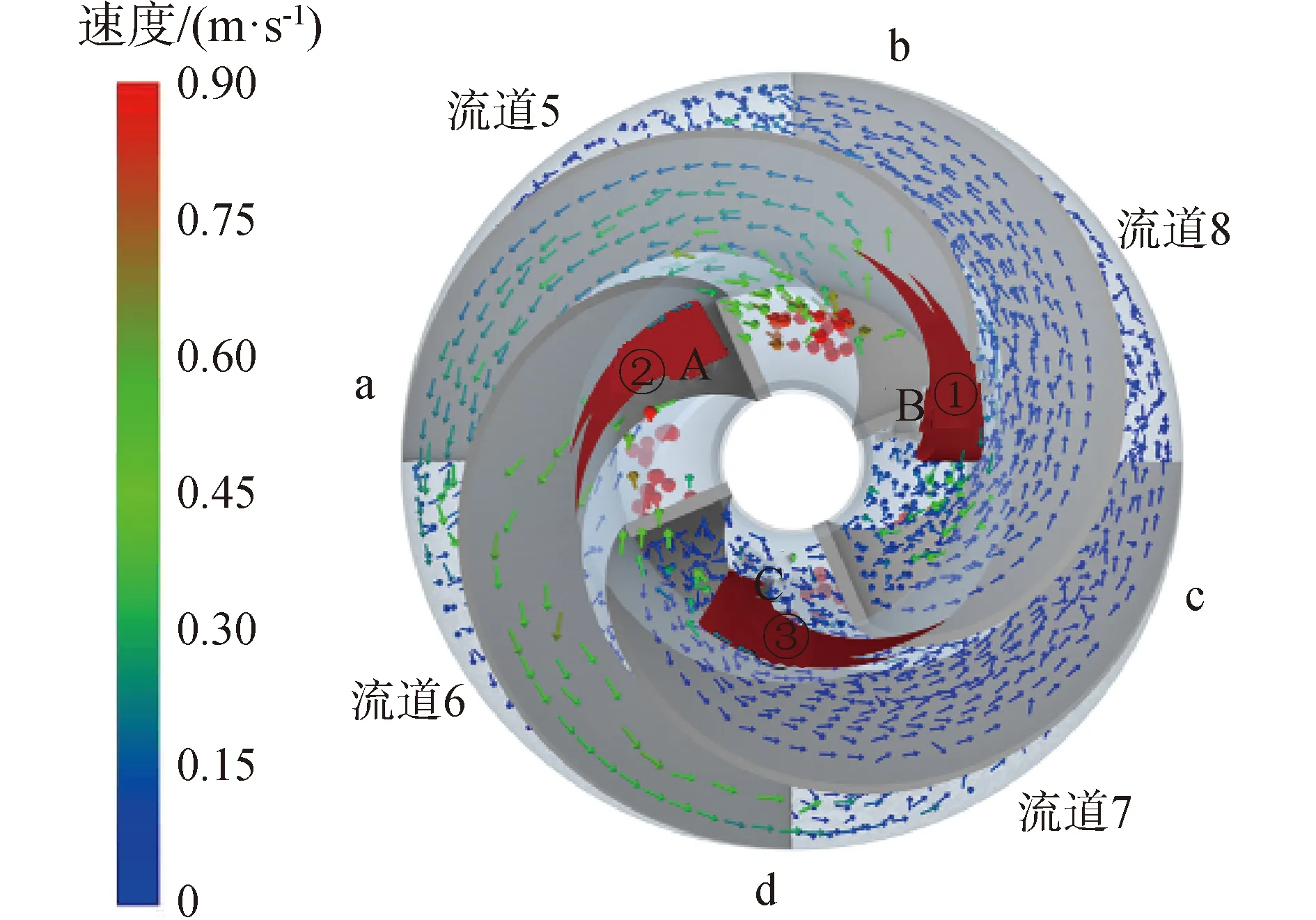
图15 两级叶轮导叶内颗粒回流速度矢量Fig.15 Particle velocity vector in two-stage pump

2.3 混合粒径颗粒群回流

在实际生产过程中，矿浆颗粒不可能是单一粒径的颗粒，对混合粒径颗粒群在泵内的回流情况进行分析十分必要，颗粒群粒径呈正态分布，数学期望值为12.5，标准差为2.5，同时限定颗粒粒径范围为5～20 mm，颗粒群的入射条件按照体积浓度5%计算。

混合粒径颗粒群在两级泵内的颗粒分布随时间变化情况如图16所示，颗粒群的体积随时间变化如图17所示。在相同的入射条件下，单一粒径颗粒的回流通过性要明显好于混合粒径颗粒，相同时刻整泵和不同级叶轮导叶内的混合粒径颗粒的总体积均更多，颗粒塞积更加严重。不同粒径颗粒在发生堆积时，小粒径颗粒填充进大颗粒的缝隙中，颗粒群塞积更加严重。同时，对泵内颗粒的平均粒径进行计算，泵内平均颗粒粒径为12.54 mm，次级叶轮导叶内颗粒平均粒径为12.31 mm，首级叶轮导叶内颗粒平均粒径为12.96 mm。泵内总体平均粒径与入射平均颗粒粒径相差不大，说明不同粒径颗粒在计算域内的质量比例与入射时相同，不同粒径颗粒回流过泵的通过时间基本相同，无特殊粒径颗粒滞留计算域；在第一级叶轮导叶内颗粒的平均粒径低于入射平均粒径，大粒径颗粒的通过次级叶轮导叶内的时间要短于小粒径颗粒，在次级叶轮导叶内存在更多的小粒径颗粒。在首级叶轮导叶内的情况刚好与次级叶轮导叶相反，这与不同级叶轮导叶内颗粒回流的堵塞程度不同有关，次级叶轮导叶内颗粒的塞积情况比首级叶轮导叶更严重，在颗粒塞积时大粒径颗粒有更好的流动性，同理，在首级叶轮导叶内堵塞程度较轻，小粒径颗粒的回流通过性更好。

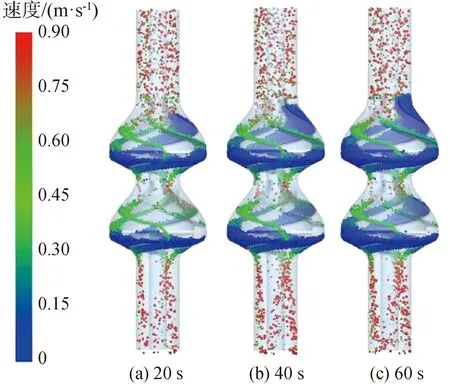
图16 不同时刻两级叶轮导叶内混合粒径颗粒分布Fig.16 Mixed size particles distribution in two stage-pump at different moments

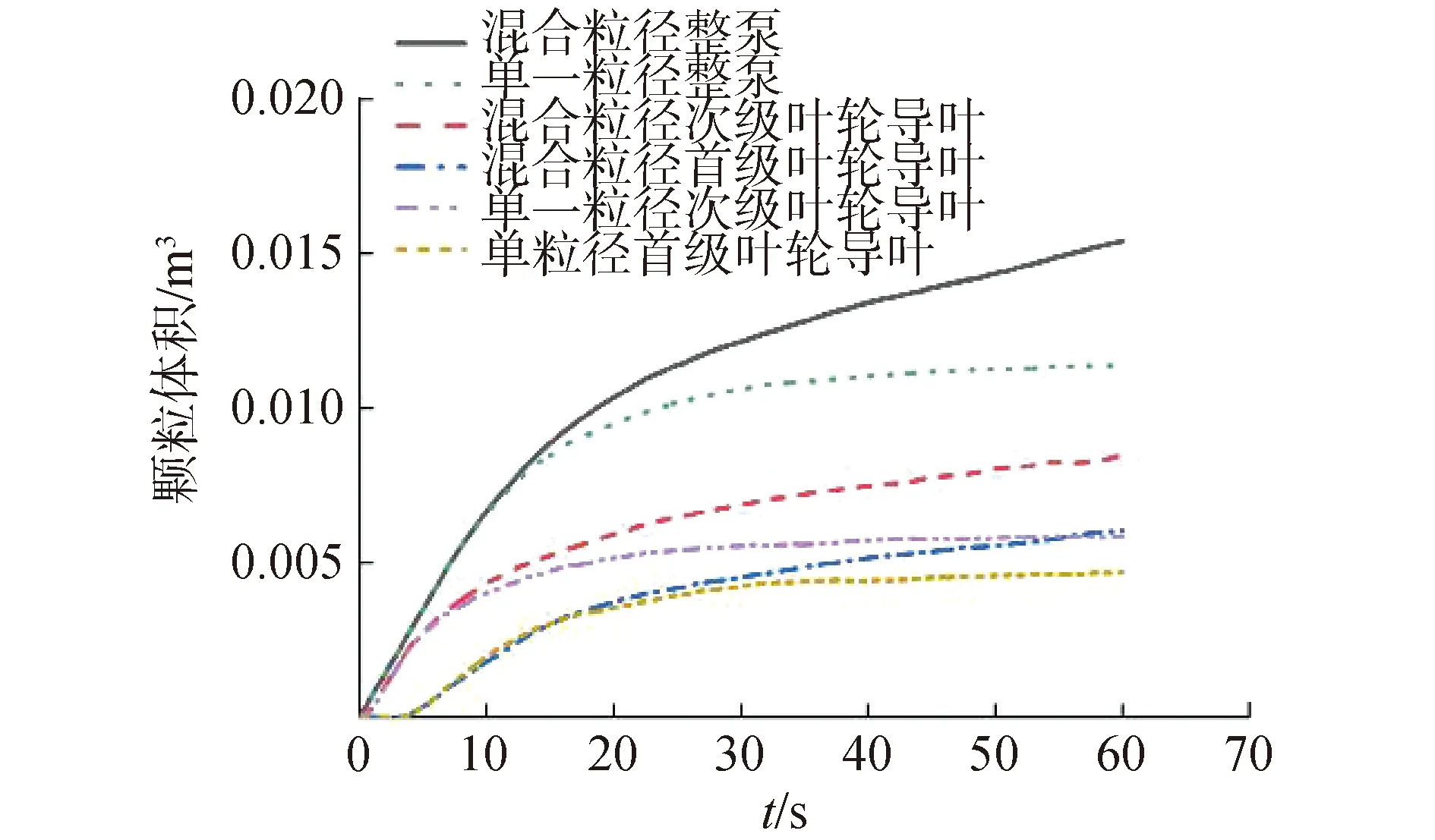
图17 两级叶轮导叶内混合粒径颗粒总体积随时间变化Fig.17 Variation of mixed size particle volume in two-stage pump with time

2.4 非球形颗粒回流

在实际工程应用中，颗粒并不是规则的球形，而是不规则的形状，颗粒形状在决定固体颗粒的行为中起着一定作用，因此对不规则形状颗粒的回流情况进行数值计算十分必要。本文采用目前公认的较为有效的多球体模型进行计算。

如图18所示，本文选取3种典型的多球组合形状和标准的球形颗粒进行数值计算，分析不同颗粒形状对回流的影响，不同多球模型的单颗粒体积与20 mm粒径球形颗粒相同，颗粒的入射条件与20 mm粒径球形颗粒相同。计算结果如图19所示，球形颗粒的质量流出速率为1.635 98 kg/s，Dual颗粒的质量流出速率为0.358 06 kg/s，Triple颗粒的质量流出速率为0.269 38 kg/s，Square颗粒的质量流出速率为0.215 51 kg/s，相对于球形颗粒，多球组合形状的颗粒在泵内的回流能力更差，非球形颗粒的球度越小，回流性能越差。两级叶轮导叶内不同形状颗粒群旋转角速度随时间变化情况如图20所示，球形颗粒在回流时更多的滚动过程，非球形颗粒尤其是Triple模型和Square模型在回流时更多的是滑动过程；非球形颗粒在相互堆积过程也更容易卡死，形成严重堵塞。因此，实际工程应用中，矿浆泵的设计阶段要充分考虑输送介质颗粒的球度，留有一定的设计余量。

图18 4种典型颗粒形状Fig.18 Four typical shapes of particles

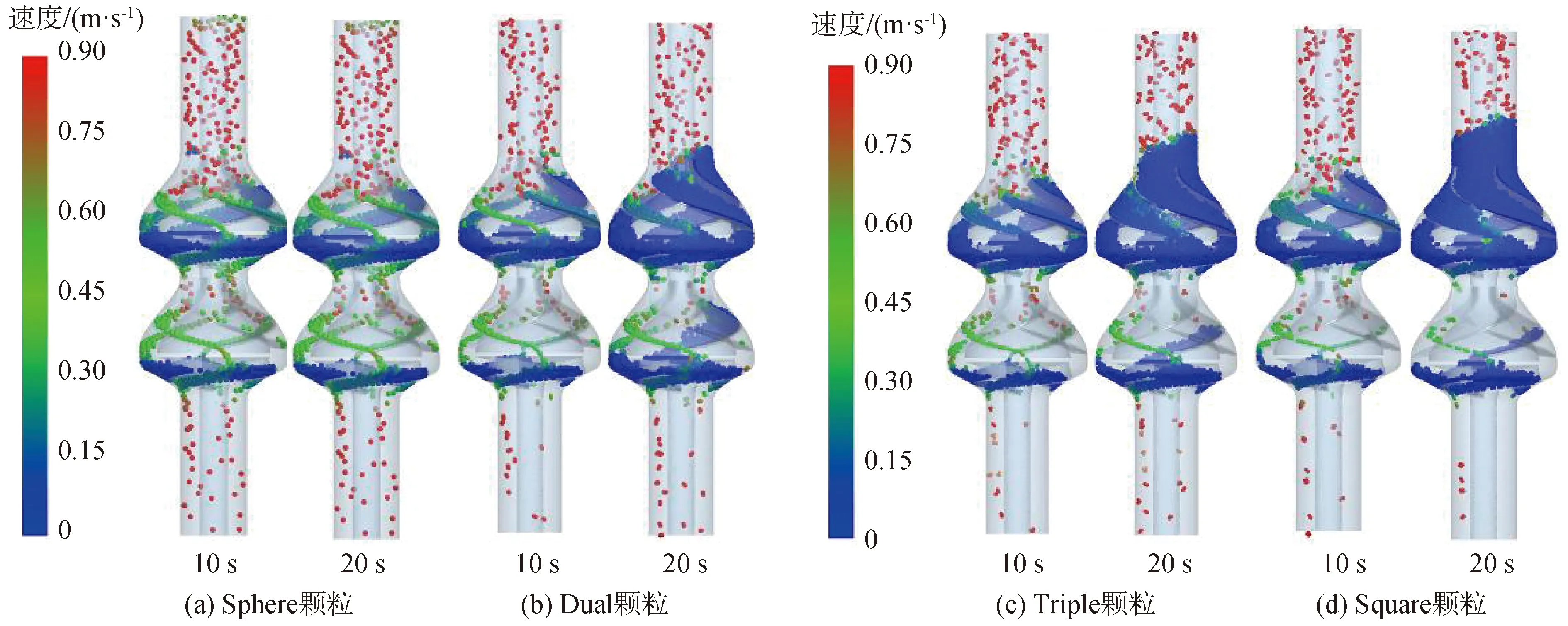
图19 两级叶轮导叶内不同形状颗粒群分布随时间变化Fig.19 Particles of different shapes distribution in two stage-pump at different moments

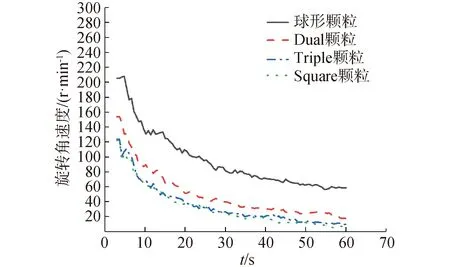
图20 两级叶轮导叶内不同形状颗粒群旋转角速度随时间变化Fig.20 Particles’ angular velocity of different shapes in two stage-pump at different moments

2.5 试验验证

为验证数值模拟结果的准确性，选择使用颗粒平均粒径为20 mm的矿石颗粒进行回流试验，颗粒粒径范围为18～22 mm，颗粒形状为椭球型，颗粒大小及形状如图21(a)所示。通过安装在两级泵底部的网状颗粒收集装置回收矿石颗粒，颗粒收集装置如图21(b)所示。如图21(c)所示，试验时将两级泵连同颗粒收集装置一同放入水中，通过泵出口将颗粒投入泵出口。

图21 回流试验装置Fig.21 Reflux test unit

投入50 kg颗粒后，将两级泵提出水面，颗粒收集装置内有49.53 kg颗粒。如图22，泵出口处有颗粒堵塞，4个导叶通道中有3个通道无颗粒塞积，一个通道已被颗粒堵满。试验结果与2.2节中数值模拟结果基本相同，验证了数值模拟的准确性。

图22 导叶出口处的颗粒堵塞情况Fig.22 Particle blockage at the outlet of guide vanes

3 结论

1)颗粒在单级叶轮导叶回流时，由于不同导叶叶片与叶轮叶片的相对位置不同，不同导叶流道内颗粒回流情况不同，导叶流道内颗粒回流情况好于叶轮流道；叶轮导叶子午面与水平方向的角度越大，颗粒在轴向方向回流情况越好，即高比转速叶轮的回流能力好于低比转速；叶轮导叶包角的角度影响颗粒在流道内的流动长度和受力，小包角叶轮导叶回流能力较好。

2)颗粒在两级叶轮导叶回流时，次级叶轮导叶内的颗粒分布情况与单级叶轮导叶基本相同，但首级叶轮导叶内颗粒群分布还受到次级叶轮叶片与首级导叶叶片的相对位置的影响，因此首级叶轮导叶流道内的颗粒分布更加不均匀。

3)混合粒径颗粒群相对于单一粒径颗粒群在泵内的回流情况更差，且混合粒径颗粒群中不同粒径颗粒在不同级叶轮导叶内通过时间不同，在次级叶轮导叶内大颗粒比小颗粒通过速度较快，在首级叶轮导叶内反之，但不同粒径颗粒通过整泵的总时间基本相同。

4)颗粒形状对颗粒在泵内的回流能力影响也很大，3种多球模型颗粒在泵内的回流能力均低于球形颗粒，而实际工程应用中，颗粒形状多数为非球形颗粒，对可回流泵的设计提出了更高的要求。