密度连续变化水体内孤立波数值模拟研究

李景远，张庆河，陈同庆

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

内孤立波是发生在密度稳定层化海水内部的一种波动，是实际海洋环境中常见的海洋动力学现象．内孤立波在传播过程中所携带的巨大能量可诱发水体强烈辐聚辐散和突发性强流[1-2]，对海域的生态环境、油气资源开发、水下潜航器安全等具有重要影响[3-5]，其生成、传播、演变机制研究一直受到国内外学者广泛关注．

目前关于内孤立波的研究除了一部分现场观测外[6]，主要集中于实验室物理模拟和数值模拟工作．谷梦梦等[7]对过山脊内孤立波进行了实验研究，给出了过山脊内孤立波的演变规律．黄文昊等[8]基于内孤立波理论解发展了一种双推板内孤立波实验室造波方法，根据实验结果分析了KdV、eKdV、MCC和mKdV 理论的适用条件．黄鹏起等[9]在二维内波水槽中研究了内孤立波在斜坡上的演变过程，分析了内孤立波破碎时的湍动能、湍流耗散率等变化规律．Kao 等[10]配置了具有有限厚度密度跃层的内孤立波水槽，结果表明，相较于两层模型，密度跃层的存在会削减内孤立波的传播速度．Segur 等[11]的实验也有类似结论．杜辉等[12]、武军林等[13]、黄文昊等[14]、王玲玲等[15]利用重力式分层流水槽研究了内孤立波对水中结构物的作用．这些实验研究对认识内孤立波生成和演变以及内孤立波对结构物的作用具有重要意义，但实验研究受到实验室尺度等的制约，数值模型可以弥补这方面的不足，已成为内孤立波研究的重要途径．付东明等[16]、黄文昊等[17]基于两层流体模型，结合内孤立波理论，通过双推板、速度入口、质量源造波等方法，建立了内波数值水槽，并获得了与理论解吻合良好的模拟结果．关晖等[18]基于Navier-Stokes 方程，使用开源软件Gerris 模拟建立了密度强分层内孤立波数值水槽，并研究了有航速潜艇遭遇内孤立波时的流场形态和受力载荷特性.徐鑫哲[19]基于势流理论，利用Fluent 模拟平板拍击造波过程建立了密度强分层二维数值内波水槽．王飞[20]基于Fluent 建立了密度强分层的三维内波数值水槽，研究了内孤立波波致流场及其对竖直圆柱体的荷载特性．

总体来看，现有大多数数值模型研究采用忽略密度跃层厚度的两层流体模型来研究内孤立波．亚洲海洋国际声学实验(ASIAEX)的定点温度链现场观测数据表明，我国南海沿水深方向存在一定厚度的密度跃层，这是南海内孤立波频发的先决条件[21-22]．从海洋的实际物理环境看，两层流体的密度强分层模型不能完全表征实际海洋环境下内孤立波的真实特性.

为此，为了克服强分层模型对于内孤立波数值模拟的不足，本文通过求解Navier-Stokes 方程和密度输运方程，建立密度连续变化内孤立波数值模型，并对其进行合理性验证．本文的内容安排如下：第1 节对本文模型控制方程和离散过程进行描述；第2 节给出密度连续变化内孤立波数值水池的实现过程；第3节对数值模拟网格敏感性进行分析，推荐合适的网格尺度；第4 节对模型的合理性进行验证，分析和研究密度连续变化流体中内孤立波的传播、演变特性，并与传统两层流体模型进行比较．

1 控制方程与数值算法

1.1 控制方程

本文基于开源软件OpenFOAM，通过添加密度输运方程，创建了密度连续变化的不可压缩流体新求解器iswFoam．由于实际海洋环境中稳定密度跃层的密度变化较小，故引入Boussinesq 近似是合适的．本文模型流体的控制方程为考虑Boussinesq 近似的雷诺时均N-S 方程(RANS)[23]，即

1.2 控制方程离散及数值求解

采用有限体积法对第1.1 节中的控制方程进行求解，变量均定义在单元中心．在(t ,t+Δ t)时段内，对控制体单元P 做时间空间积分，将控制方程式(1)和(6)微分方程转化为如下积分方程：

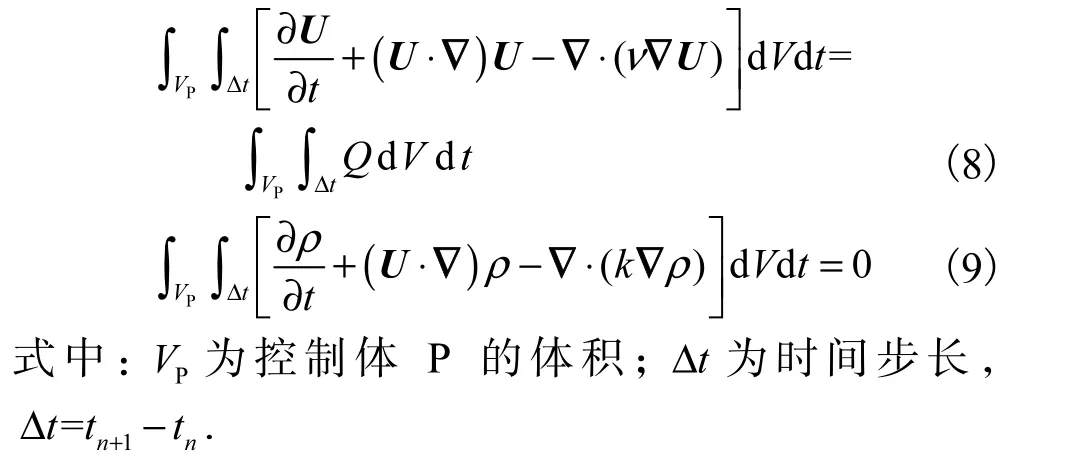
有限体积法离散过程中应用高斯定理将体积分转化为面积分，再将所得面积分形式转化为单元体各面累加求和的形式．下面以积分形式的密度扩散项(式(10))为例说明这一过程，图1 为离散过程中所需参量的示意．

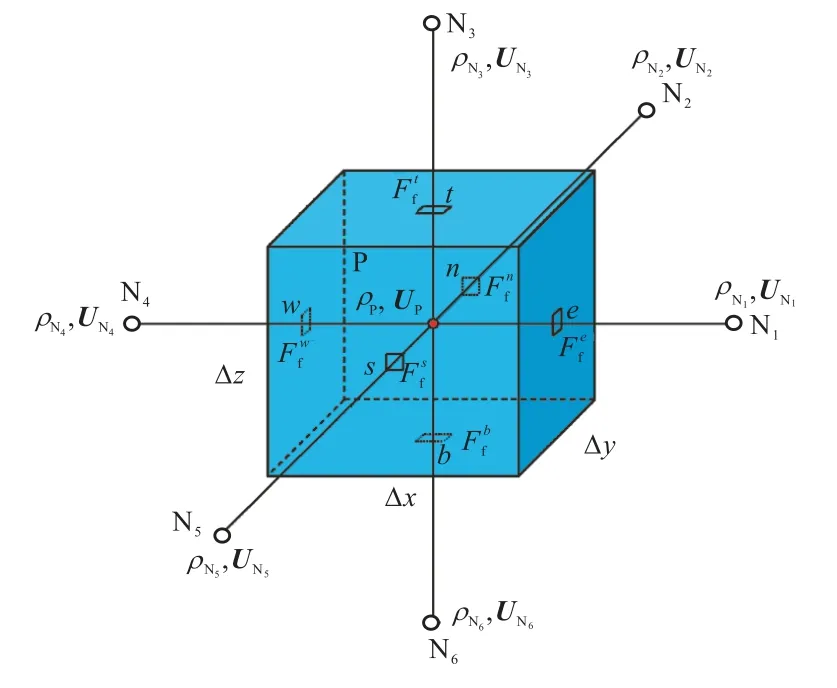
图1 三维笛卡尔坐标系下密度扩散项的离散示意Fig.1 Schematic of the density diffusion term in a discrete elements in a three-dimensional Cartesian coordinate system

按照上述离散过程，可获得动量方程式(8)和密度对流扩散方程式(9)的离散形式为

动量方程对流项中非线性项采取线性化处理，即对流项通量采用当前时刻已知的通量．为了防止同位网格系统下求解出现压力棋盘效应，面上的速度计算采用Rhie-Chow 差值[25]．

离散后的速度压力耦合方程采用pimple 算法求解，pimple 的基本思想是将每个时间步长内用simple稳态算法求解(也就是将每个时间步内看成稳态流动)，时间步长的步进用piso 算法来完成[26]．每个时间步长内，速度压力求解完成后，将速度代入离散后的密度对流扩散方程式(12)便可求出下一时刻的密度场ρn1+，更新速度场用于下一时刻求解．

2 内孤立波的生成

目前，描述内孤立波的理论主要有KdV、eKdV、mKdV、MCC 理论等[27]，这些理论模型的解析解均基于密度强分层的两层流体模型给出．对于更接近实际的密度连续变化情况下的海洋内孤立波，目前尚未见到解析解，因此内孤立波的生成仍按两层流体解析解给定初值．本文选用可模拟大振幅内孤立波的eKdV 方程理论解作为初值．

2.1 eKdV方程及其稳态解

在图2 所示的坐标系中，设未受扰动的两层流体界面位于Oxy 平面，坐标原点在两层界面处，内孤立波沿Ox 轴正向传播．设各层均为不可压缩流体，上层流体厚度和密度分别为 h1和 ρ1，下层流体厚度和密度分别为 h2和 ρ2．ζ ( x, t)表示内孤立波的波面函数，则eKdV 理论的内孤立波控制方程及其稳态解[8]如下：

式中：1u 和 u2分别为上、下层流体水质点平均水平速度；a 为内孤立波振幅；λeKdV为内孤立波的特征波长；ceKdV为内孤立波理论解的相速度．

当c3＝0 时，eKdV 方程即可退化为KdV 方程，eKdV 理论解退化为KdV 理论解．

图2 两层流体内孤立波示意Fig.2 Schematic of ISWs in a two-fluid system

2.2 内孤立波的生成

利用第2.1 节中内孤立波波面理论解ζ 以及上、下层平均水平速度1u 和 u2对计算域进行初始化.Yang 等[28]在中国南海密度分布的研究发现，冬季南海的密度垂向分布呈现双曲正切型式，大多数学者在进行南海潮流、内波等研究时，亦主要采用双曲正切型式，如Chen 等[29]和Lamb[30]．基于南海的实际情况，本文密度的初始垂向分布采用Aghsaee 等[31]提出的双曲正切形式，即

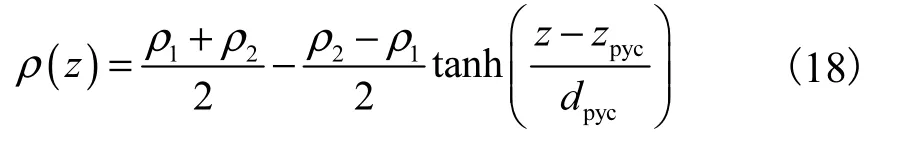
式中：ρ ( z )为计算域内连续变化的密度场；ρ1为计算域顶部的密度值；2ρ 为计算域底部的密度值；zpyc为密度跃层中心位置；dpyc为密度跃层厚度的1/2；z为垂向坐标，当dpyc趋近于0 时，密度跃层厚度趋近于0，此时密度连续变化模型可转化为两层流体模型.

3 内孤立波模拟网格敏感性分析

在对内孤立波进行模拟时，需要选择合理的网格尺度和时间步长，以在获得所需模拟精度的条件下提高计算效率．由于内孤立波理论波长为无限长，因此需要对内孤立波波长进行合理简化，确定适合分析的有效波长．下面通过引入有效势能(available potential energy，APE)概念，确定合理的有效波长，并在此基础上进一步讨论内孤立波模拟的网格尺寸．

3.1 内孤立波“有效波长”的确定

考虑一个二维区域( x, z)∈[－l , l] × [－H,0]，内孤立波有效势能[32-33]可定义为

设波长λ所对应的截取有效势能为APEλ，利用总有效势能对其进行无量纲化得APEnon＝APEλ/APEt，无量纲截取有效势能APEnon亦可理解为截取势能占总势能的百分比．

利用Michallet 等[34]提出的内孤立波特征波长L对波长λ进行无量纲化，得

特征波长L 的计算式为

基于 eKdV 理论，在上、下层水深比分别为h1/h2＝1/9、2/8 和3/7 的条件下，设置系列波高，通过计算一系列波长λ所对应的截取有效势能APEλ，获得APEnon随λnon的变化规律，如图3 所示．由图3 可知，因为内孤立波能量主要集中于波峰附近区域，APEnon随λnon增大而迅速增大趋近于1．在相同水深比情况下，较大波高对应的APEnon随λnon更快趋近于1，主要原因为集中在内孤立波中间区域的有效势能随波高的增加所占总势能比重增大．总体来看，当APEnon＞99.8%时，所截取的有效势能随着波长的增加几乎不产生变化，因此，取APEnon＝99.8%时所对应的波长作为有效波长λA是合理的，能充分反映内孤立波的特性．下面的有关讨论主要结合λA进行．

图3 无量纲有效势能随波长变化关系Fig.3 Relationship of dimensionless available potential energy with wavelength

3.2 空间步长测试

以h1/h2＝2/8、波高H＝16.5 cm 为例分析计算空间步长对模拟结果的影响，测点设置在距离造波中心8λA处．表1 和表2 列出了内孤立波在不同网格系统下传播至8λA位置测点的波高结果及其与理论解的对比．

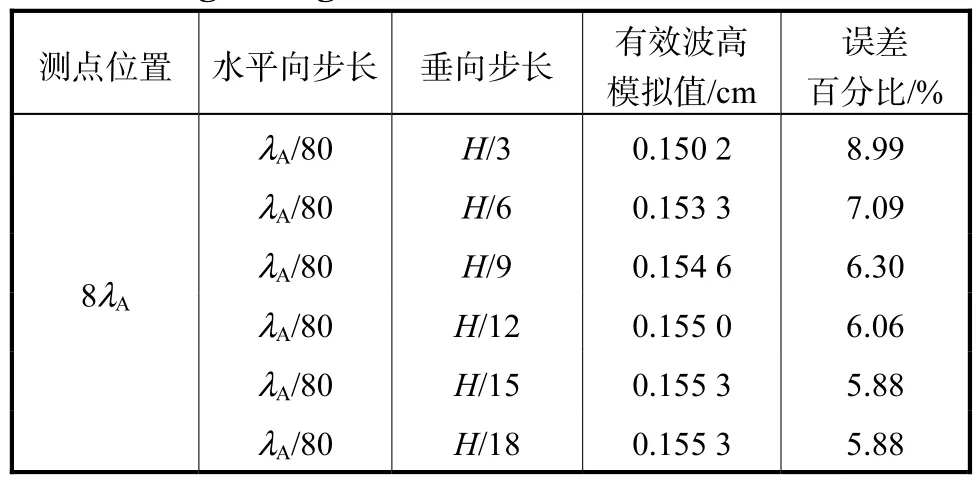
表1 垂直方向波高范围内空间步长测试取值Tab.1 Values of the space step test in the vertical wave height range

表2 沿波浪传播方向空间步长测试取值Tab.2 Values of the space step test along the wave propagation direction

由表1 可知，随着垂向步长的减小，测点位置处的波高值逐渐增加，误差逐渐减小，且在垂向步长减小至H/15 时趋于稳定．由表2 可知，水平向步长Aλ/20 误差率最大，水平向步长达到Aλ/80 后，误差随着步长的减小基本不再减小，同时波高基本稳定．综合考虑波形分辨率和计算效率，本文模型水平向步长取Aλ/80、垂向步长取H/15 是合适的．

4 数值模拟结果与分析

4.1 算例设置

本文结合黄文昊等密度强分层水槽实验，设置一系列数值算例(表3)．内孤立波数值水槽长150 m，总水深为1 m，密度分布按照式(18)设定，其中ρ1为998 kg/m3、ρ2为1 025 kg/m3．计算域内网格尺寸：水平向步长取λA/80；垂向步长取H/15．

表3 算例列表Tab.3 Detailed settings of the cases

4.2 数值模拟结果与理论解的对比及分析

为验证本文密度连续变化内孤立波模型(iswFoam)的造波能力，选取不同时刻的波面场图与理论解进行对比．图4 以工况1 为例给出了密度等值线分布，图中黑色实线为浮频率最大时对应的等密度线，将该等密度线作为本文分析的内孤立波波面．

图5 给出了表3 中4 种工况连续分层内孤立波波面数值造波结果，并与相同条件下的eKdV 理论解进行了比较．结果表明，数值造波结果与理论解基本一致，波高的误差百分比小于2%，本文模型对于不同上下层水深比，不同波高条件，均能造出符合理论解的内孤立波．图6 给出了工况4 不同时刻的密度场图，由图可知内孤立波在传播过程中，波面稳定传播，且清晰无破碎．

图4 密度等值线分布Fig.4 Schematic diagram of density contours

图6 不同时刻密度场图(工况4：h1/h2＝3/7，a＝16.5 cm)Fig.6 Density contours of different time(Case 4：h1/h2＝3/7，a＝16.5 cm)

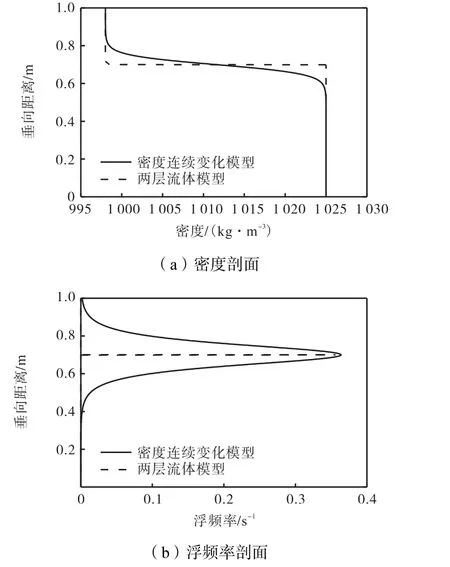
图7 密度连续变化模型与两层流体模型的密度剖面及浮频率剖面Fig.7 Density profile and buoyancy frequency profile in continuously stratified and two-layer fluid model

图8 密度连续模型与两层流体模型内孤立波传播数值模拟结果Fig.8 Comparison of numerical simulation results of internal solitary wave propagation in continuously stratified and two-layer fluid model

4.3 密度连续变化与两层流体模型的对比

为了比较密度连续变化和强分层模型的不同，利用OpenFAOM 多相流模型对密度强分层内孤立波进行模拟．图7 给出了密度连续变化与两层流体模型的密度剖面及浮频率剖面的对比情况，其中流体浮频率为1 000 kg/m3．对于强分层模型，除了密度分布不同，算例其他设置均与本文模型相同，图8 以工况2 和工况4 为例，给出了两种模型的模拟结果．图8 表明，受密度跃层的影响，密度连续变化模型的内孤立波波速(cpyc)小于强分层模型中的内孤立波波速(ctwo)，即密度跃层的存在使内孤立波波速相对于密度强分层条件有所减小．两层流体的密度强分层模型本质上忽略了实际海洋环境下的密度跃层厚度，可能过高估计了实际海洋中内孤立波传播速度．该结论与Kao等[10]和Segur 等[11]的实验结果一致，即相较于强分层模型，有限厚度密度跃层的存在会削减内孤立波的传播速度．Thiem 等[35]也得到类似的结论，指出两层流体模型的内孤立波波速结果高于实测结果．值得注意的是，虽然本文密度垂向分布选用双曲正切型式，但是通过Segur 等[11]的实验分析可知只要存在密度跃层，两层流体中的内孤立波波速就会被削减，所以采用其他型式的密度垂向分布也会得到与本文相同的结果．

对于同一种工况，除了密度方面的不同，两种模型的初始条件、算例设置及网格均相同，所以相同工况下初始时刻的总能量和传播过程中的数值耗散是相同的．在总能量和数值耗散相同的情况下，两层流体模型的内孤立波衰减大于本文密度连续变化模型(图8)，表明两层流体模型由于忽略密度跃层厚度，可能导致其过高估计实际海洋环境下内孤立波传播过程中的能量耗散及波高衰减．

4.4 紊流影响分析

为了分析前文各个工况下紊流对内孤立波传播演变过程的影响，图9 给出了工况2 所对应的紊流动能耗散率．由计算结果可知，内孤立波稳定传播时，最大紊流动能耗散率出现在波谷附近的跃层内，量级为10-6，紊流对内孤立波的稳定传播以及密度场的变化几乎无影响，这一结论与Small 等[24]研究内孤立波时给出的结论一致．需要指出的是，本文主要对内孤立波的稳定传播过程进行了模拟，在研究浅水区内波破碎等过程时紊流的影响是不可忽略的．

图9 紊流动能耗散率结果(工况2，t＝100 s，蓝色实线为等密度线)Fig.9 Graph of results of turbulent energy dissipation rate(Case 2，t＝100 s，the solid blue line represents the iso-density line)

5 结 论

本文基于雷诺时均Navier-Stokes 方程，加入密度输运方程，将内孤立波理论解作为初始场，建立了密度连续变化内孤立波数值模型，并对其合理性进行了验证．通过引入有效势能概念，将内孤立波的无限波长合理简化为有效波长，并对数值模拟时在保证模拟精度前提下的合理网格尺寸进行了分析．在此基础上，探讨了密度连续变化模型与两层流体模型的差异性．主要结论如下．

(1) 本文所建模型在不同上、下层水深比(h1/h2)、不同波高条件下均能造出符合理论解及符合传播演变规律的内孤立波．

(2) 对于 eKdV 理论，将无量纲化有效势能APEnon＝99.8%时所对应的波长取为有效波长Aλ是合理的，能充分反映内孤立波特性．

(3) 综合考虑波形分辨率和计算效率，推荐内孤立波模拟水平向空间步长取1/80 有效波长，垂向空间步长取1/15 内孤立波波高．

(4) 两层流体模型由于忽略密度跃层厚度，导致其可能过高估计实际海洋环境下内孤立波的传播速度和波高衰减．

本文所建模型考虑了密度的连续变化和密度跃层的厚度，更接近实际海洋环境情况，能更好地反映实际海洋环境下内孤立波的各项特性．